基于改进Knothe 时间模型的地表移动延续时间预测

2023-12-11张亮亮姚直书王晓健

煤炭学报 2023年11期

张亮亮，程桦,2 ，姚直书，王晓健

(1.安徽理工大学土木建筑学院, 安徽淮南 232001；2.安徽大学资源与环境工程学院, 安徽合肥 230022)

煤层开采后顶板发生垮落、断裂变形，该变形逐渐向上传递引起地表发生移动变形，导致地面沉降、建筑物及基础设施受损，严重影响矿区居民生命财产安全[1-2]。大量研究表明，地表移动变形过程一般分为初始阶段、活跃阶段和衰退阶段，且在衰退阶段连续6 个月累计地表下沉量不超过30 mm，则认为地表移动与变形达到稳定状态，这3 个阶段经历的时间总和为地表移动延续时间[3]。受地层构造和流变特性等因素影响，煤层开采结束后地表移动变形并没有立即停止，而是存在明显的滞后现象，自煤层停采至地层移动变形最终稳定这段时间内地表建(构)筑物仍可能发生破坏。因此，精确预计地表移动延续时间对于地表及地面设施的稳定性评估至关重要。

20 世纪50～60 年代，我国开始建立开采地表沉降监测站，获得了大量的地表移动变形监测数据，为地表移动延续时间预测模型建立提供了数据支撑。《建筑物、水体、铁路及主要井巷煤柱留设与压煤开采指南》(以下简称“三下开采指南”)考虑了煤层平均采深的影响，分别给出了平均采深大于400 m 和小于400 m 开采条件下地表移动延续时间的经验计算公式[4]；张广伟等[5]分析了覆岩岩性、采深、开采速度、开采尺寸、采厚和顶板管理方法对地表移动延续时间的影响，采用数理统计的方法获得了地表移动延续时间计算公式；郑志刚等[6]采用回归分析的方法，得到厚松散层综放开采条件下地表移动延续时间与松散层厚度和采深的关系；安士凯等[7]综合考虑了采深、采厚、松散层厚度和工作面开采速度等地表移动延续时间影响因素，采用拟合的方法建立了厚松散层矿区地表移动延续时间计算模型；美国西弗吉尼亚大学PENG[8]给出了能够考虑采深、工作面开采速度和边界角等影响因素的地表移动延续时间计算公式；李春意等[9]考虑了采动程度、覆岩岩性和采深等多种因素的影响，提出了非充分采动条件下地表移动延续时间的经验计算公式。

上述地表移动延续时间预测模型主要是经验公式和基于实测数据拟合获得的，针对特定地质条件和开采条件下预测精度较高，但由于不同矿区煤炭资源赋存条件和开采强度差异较大，上述模型难以精确预测不同煤层采高、采深和煤层开采速度等条件下地表移动延续时间，主要存在以下3 点不足：① 地表移动延续时间预测模型主要是依靠现场施工经验或基于监测数据拟合得到的，理论基础薄弱，而且各经验公式形式不统一，不利于推广应用；② 经验模型参数确定方法不一致，使得各矿区估算的模型参数相差较大，最终预测的地表移动延续时间与实际情况误差较大，预测精度低；③ 经验公式考虑的地表移动延续时间影响因素较少，难以充分体现煤层采高、采深和煤层开采速度等因素的影响。因此，亟待建立一种表达形式简单、模型参数数量少且易确定、精度高、适用性强的地表移动延续时间预测模型。

笔者在经典Knothe 时间模型的基础上，提出新的模型假设，建立仅含一个模型参数且与实际地表动态沉降规律一致的改进Knothe 时间模型。在此基础上，根据地表移动延续时间的定义建立了不同地质条件和开采强度条件下地表移动延续时间预测模型，采用20 个矿区地表移动延续时间监测数据验证了模型的精确性和合理性。

1 Knothe 时间模型

1952 年，波兰学者Knothe 做出了以下假设：地表某点的瞬间沉降速度与该点的最终沉降量W0和瞬间沉降量W(t)之差成正比例关系[10-11]，建立了微分方程来描述地表动态沉降过程：

式中，c为与上覆岩层力学性质有关的时间影响系数；t为时间。

对式(1)进行分离变量并结合t=0,W(t)=0边界条件，得到地表沉降量与时间的函数，即

由式(2)可知，Knothe 时间模型描述的地表沉降与开采时间呈单调增加的指数函数关系，而实际煤层开采引起的地表沉降一般经历初始阶段、活跃阶段和衰退阶段，时间近似成“S”型曲线规律，且Knothe 时间模型描述的地表沉降速度与实际情况相差较大，因此经典的Knothe 时间模型不能准确描述地表动态沉降过程[12-14]。

2 改进Knothe 时间模型

Knothe 时间模型因其参数少且函数形式简单被广泛应用，但随着研究的深入，该模型精度低的缺点逐渐显现。对此，国内外提出了大量的改进Knothe时间模型，但仍存在函数形式复杂、模型参数多、物理意义不明确和难以推广使用等不足之处，关键原因之一是由于现有改进Knothe 模型难以从Knothe 时间模型的基本假设入手，而是通过增加或修正Knothe 时间模型参数的方式加以改进，这种方法虽然能提高模型精度，但理论基础薄弱，增加或修正的模型参数物理意义不明确。为此，笔者在经典Knothe 时间模型基本假设的基础上，提出了新的模型假设，建立改进的Knothe 时间模型。

大量现场监测数据表明，煤层开采地表沉降速度与沉降量满足先从0 逐渐增加至最大值，然后由最大值逐渐减小为0 的变化规律，该规律与一元二次函数相似，故可假设

式中，k、b为系数。

研究表明，当地表沉降量约为最大沉降量的一半时，沉降速度达到最大值[15]，故有

将式(4)代入式(3)得到

根据式(5)，参考Knothe 时间模型假设，提出新的模型假设：地表某点的瞬间沉降速度与该点的最终沉降量W0和瞬间沉降量W(t)之差和瞬间沉降量W(t)的乘积成正比关系，即

式中，C为改进Knothe 模型的时间影响参数，C=-k。

解式(6)得

对式(7)两边进行积分得

式中，A为积分常数。

将式(8)进行化简得

式中，B为积分常数。

实际监测过程中难以精确地判断地表点的临界沉降时刻，通常以沉降量达到10 mm 的时刻作为沉降开始时刻[16-17]，即t=0 时，W(t) =0.01 m，根据式(9)有

将式(10)代入式(9)，得到改进Knothe 时间模型描述地表动态沉降函数为

对式(11)求时间的导数得到地表动态沉降速度v(t) 和沉降加速度函数a(t)为

根据式(11)、(12)得到不同模型参数C对应的地表动态沉降、沉降速度和沉降加速度曲线，如图1 所示。

由图1 可知，模型参数C主要影响地表达到最大沉降量的时间。C越大，时间越短；而对于地表沉降速度和加速度而言，C不仅影响达到最大沉降速度和加速度的时间，而且也影响地表最大沉降速度和加速度。C越大，地表最大沉降速度和最大加速度越大。从曲线形态看，改进Knothe 时间模型描述的地表沉降曲线近似为“S”型曲线，沉降速度速度近似为正态分布曲线，加速度近似为正弦函数曲线，这与实际情况一致，因此改进的Knothe 时间模型可用于描述地表动态移动过程。

此外，结合图1 和式(11)可知，改进Knothe 时间模型仅含一个模型参数C，相对于其他模型更有利于现场应用，相对于Knothe 时间模型而言，在没有增加参数的前提下，所描述的地表沉降、沉降速度和沉降加速度变化规律更符合实际情况，其精度得到提高。

3 地表移动延续时间预测模型建立

3.1 模型建立

煤炭开采引起的地表移动与变形是一个复杂的时间和空间问题。如图2 所示，一般认为地表沉降量达到10 mm 至沉降速度达到50 mm/月或1.7 mm/d为地表沉降初始阶段，沉降速度大于50 mm/月或1.7 mm/d 为地表沉降活跃阶段，沉降速度小于50 mm/月或1.7 mm/d，且当连续6 个月的地表累计沉降量小于30 mm 时，为地表沉降衰退阶段，这3 个阶段所经历时间的总和称为地表移动延续时间[18-19]。

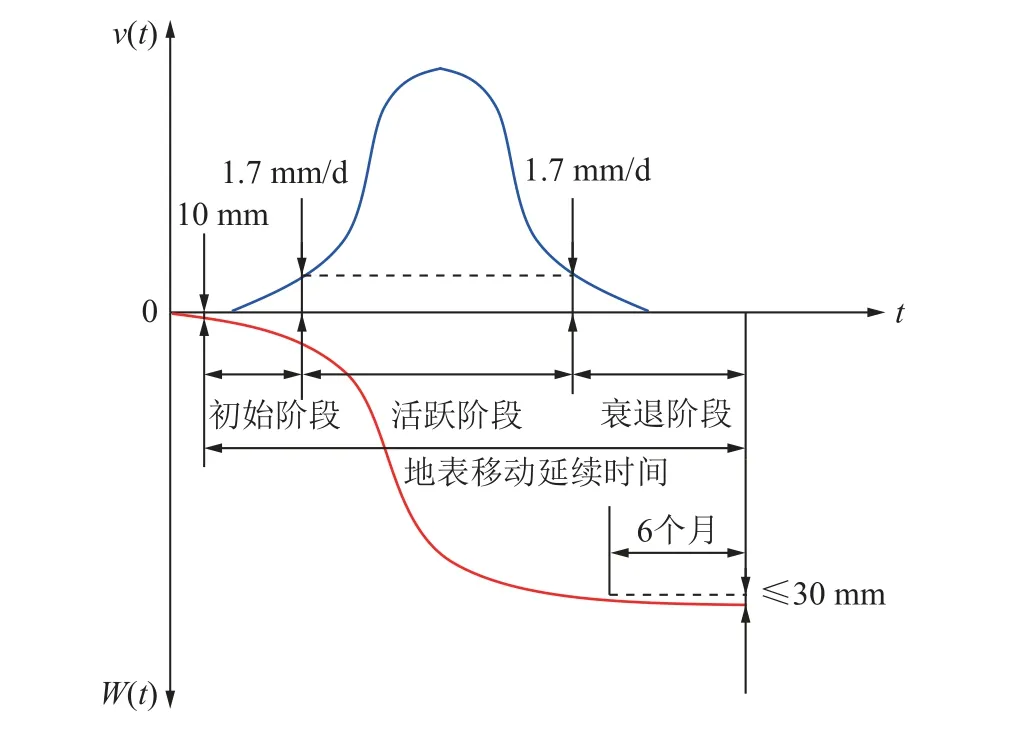
图2 地表移动3 阶段Fig.2 Three stages of surface movement

“三下开采指南”给出了地表移动延续时间计算公式为

式中，T1为“三下开采指南”预测的地表移动延续时间；H为平均采深。

式(13)表达形式不统一，且仅考虑了平均采深一个因素对地表移动延续时间的影响，因此该公式预测精度较低，适用性不广。为此，根据改进Knothe 时间模型，建立新的地表移动延续时间预测理论模型。

根据图3 和地表移动延续时间定义，当衰退阶段结束对应的时刻即为地表移动延续时间，假设该时刻为T2，根据式(11)得到此时刻地表沉降量W(T2)为

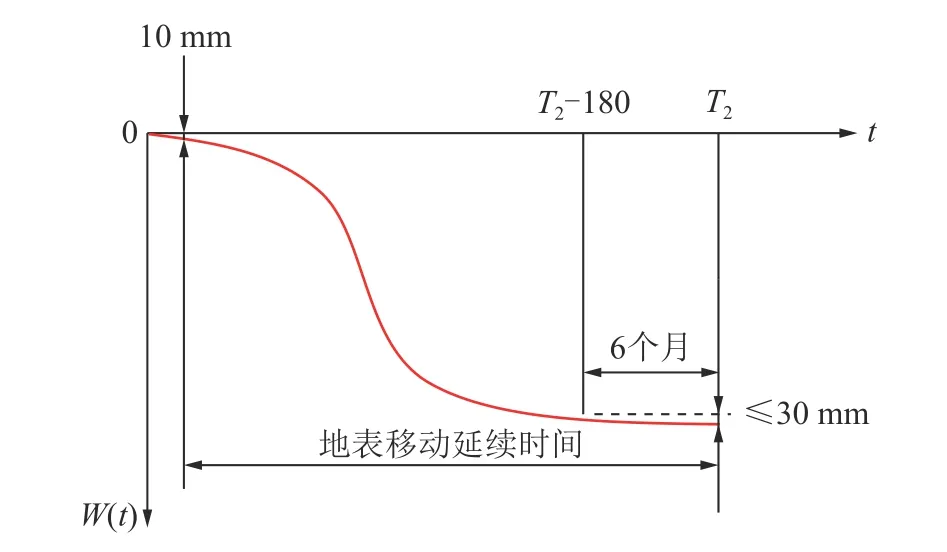
图3 地表移动延续时间计算模型Fig.3 Calculation model of surface movement duration

同时假设每个月为30 d，根据式(11)得到在地表移动稳定前6 个月的地表沉降量W(T2-180)为

根据地表移动延续时间的定义，则W(T2-180)和W(T2)两个沉降量之间需满足：

式中，T2为基于改进Knothe 时间模型预测的地表移动延续时间。

式(16)要求左边预测值≤30 mm，即当T2时刻的沉降量和T2-180时刻的沉降量之差刚好为30 mm时的T2为地表移动延续时间。由于式(16)左边预测沉降量差值的单位为“m”，而右边单位为“mm”，为了统一，式(16)可转化为

对式(17)进行化简得

式(18)即为基于改进Knothe 时间模型的地表移动延续时间预测模型，该模型是基于严格的理论推导而得，相对于传统经验预测模型，其理论基础更加扎实，而且该模型仅含一个模型参数C，便于现场应用。

根据同样的建模方法，可获得Knothe 时间模型预测地表移动延续时间计算公式为

式中，T0为Knothe 时间模型预测的地表移动延续时间。

3.2 模型参数确定

根据概率积分理论，近水平煤层开采条件下，当开采范围达到充分开采的临界值时，地表最大沉降量近似等于0.98W0[20-21]。假设开采速度为vk，采空区临界尺寸为Lf，则达到充分开采的临界时间可表示为Lf/vk，结合式(11)得到改进Knothe 时间模型影响参数C的计算公式为

由于开采速度容易确定，因此确定时间模型参数的关键在于确定达到充分开采时采空区的临界尺寸。大量研究表明，当工作面推进距离为1.4H时达到充分开采[22]，因此Lf为

将式(21)代入式(20)得到模型影响参数C的计算公式为

将式(22)代入式(18)，得到基于改进Knothe 时间模型的地表延续时间预测模型为

从式(23)可以看出，笔者建立的地表延续时间预测模型不仅能考虑平均采深的影响，而且能考虑工作面开采速度的影响。由于地表最大沉降量与煤层采高和倾角密切相关，因此预测模型能同时考虑平均采深、工作面开采速度、煤层厚度和倾角的综合影响，其适用性相对于“三下开采指南”的地表延续时间预测模型更加广泛。

4 模型验证

收集、统计20 个矿区工作面开采参数，主要包括平均采深H、煤层厚度M、煤层开采速度vk和地表最大沉降量，结果见表1。将表1 参数代入式(22)，得到改进Knothe 时间模型参数C，再将C代入式(18)，得到20 个矿区的地表移动延续时间预测值T2。同时，分别根据式(13)、(19)计算得到“三下开采指南”和Knothe 时间模型预测的地表移动延续时间T1和T0，3种模型预测结果见表2。将T2、T1和T0与各矿区地表移动延续时间监测值TM进行对比，来验证预测模型的精确性及合理性，对比结果如图4～6 所示。

表1 20 个矿区工作面参数Table 1 Parameters of working faces in 20 mining areas

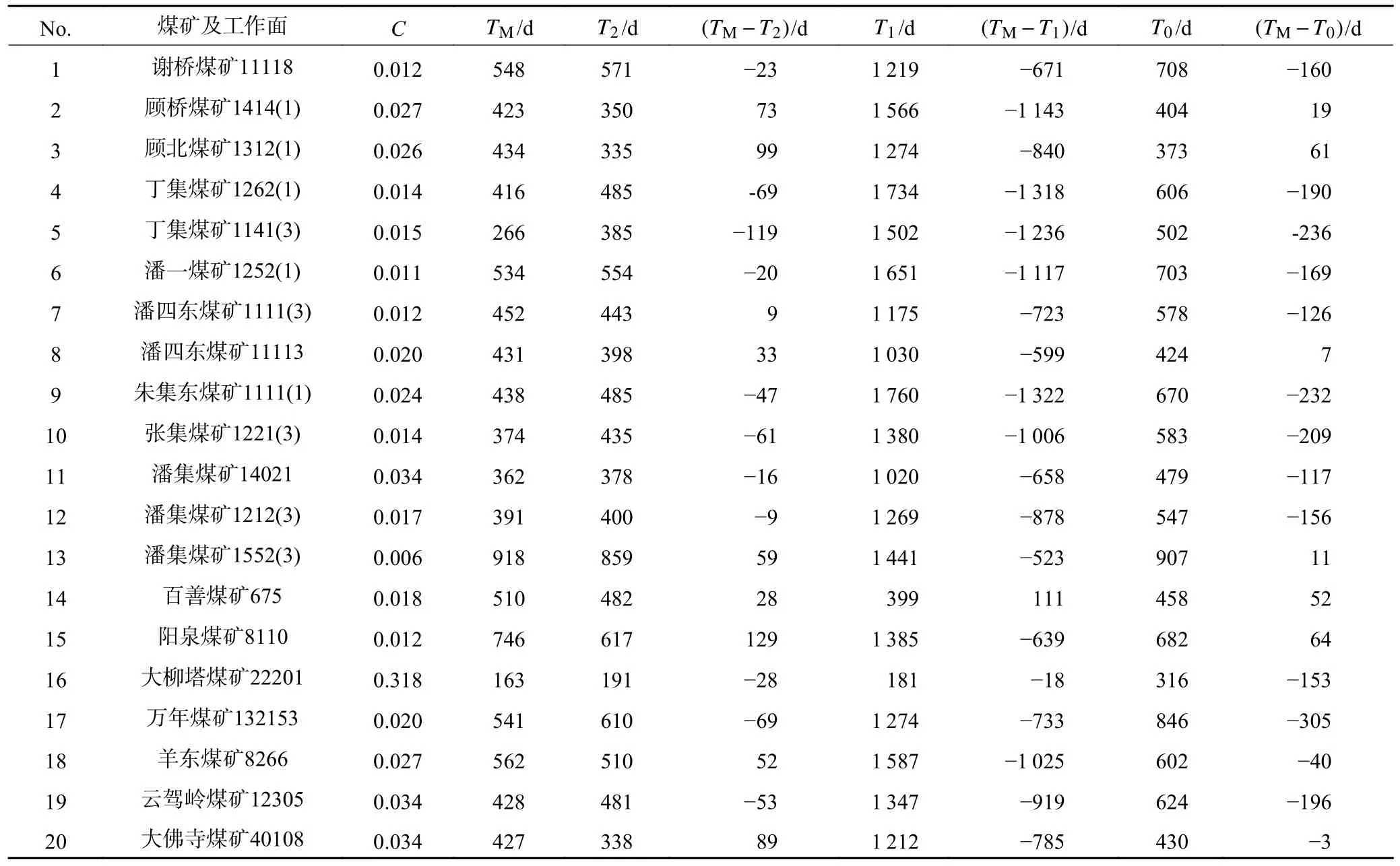
表2 20 个矿区地表移动延续时间预测值和实测值Table 2 Predicted and measured values of surface movement duration in 20 mining areas

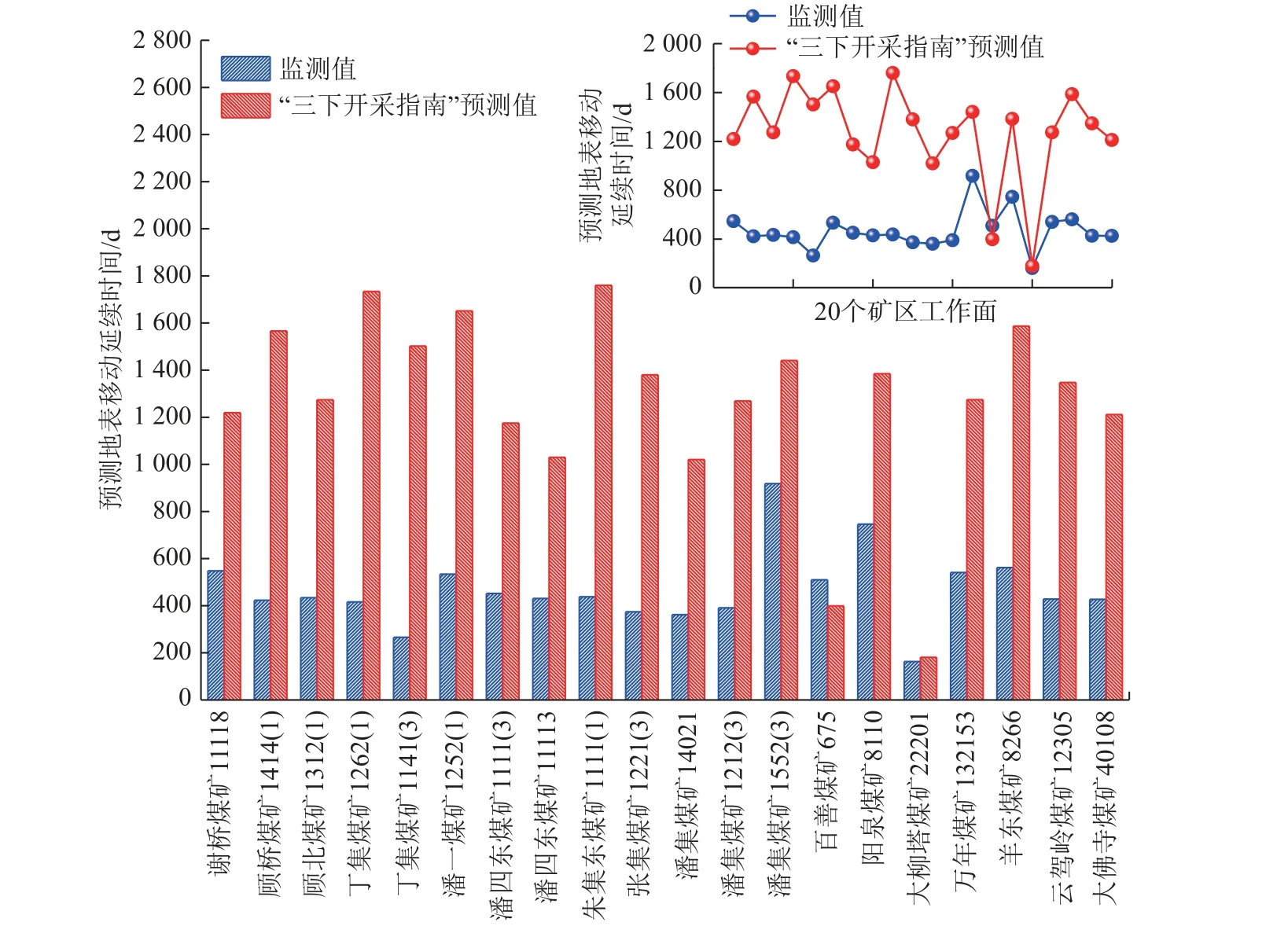
图4 “三下开采指南”预测值和实测值对比结果Fig.4 Comparison between predicted value of “Three underground mining” and measured value

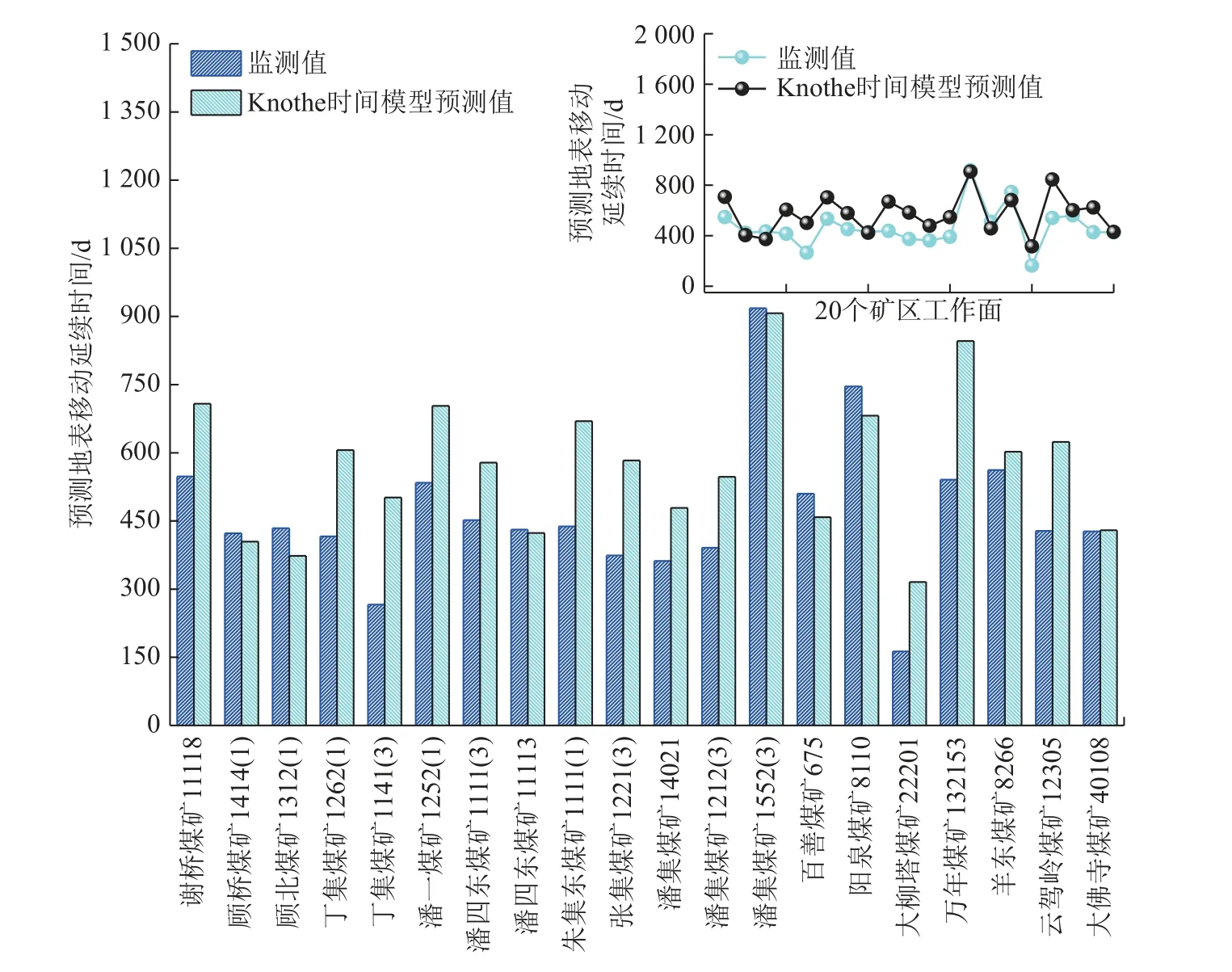
图5 Knothe 时间模型预测值和实测值对比结果Fig.5 Comparison between predicted values of Knothe model and measured values

由表2 和图4、5 可知，20 个矿区地表移动延续时间实测值和“三下开采指南”预测值相差较大，预测精度低。当平均采深大于400 m 时，预测值和实测值最小相差523 d，最大相差1 322 d；当平均采深小于400 m 时，预测值和实测值最小相差18 d，最大相差111 d。说明“三下开采指南”预测公式主要适用于平均采深小于400 m 的情况，当平均采深超过400 m 后，该公式预测精度较低，适用性不强。Knothe 时间模型预测精度要明显高于“三下开采指南”，但20 个矿区中，有12 个矿区的地表移动延续时间预测值和实测值的误差超过100 d，因此该模型的预测精度仍较低。

由表2 和图6 可知，20 个矿区地表移动延续时间实测值和本文建立的模型预测值基本吻合，预测精度高，验证了模型的合理性和精确性。同时，20 个矿区平均采深变化范围为72.5～920.0 m，煤层厚度变化范围为1.8～10.7 m，开采速度变化范围为1.0～ 9.6 m/d，而本文建立的地表移动延续时间预测模型预测结果与实测结果接近，两者最小相差仅9 d，说明该预测模型适用性较强，能用于不同地质条件和不同开采强度的地表移动延续时间预计。

图6 改进Knothe 时间模型预测值和实测值对比结果Fig.6 Comparison between predicted values of improved Knothe model and measured values

为了进一步验证本文建立的预测模型精度，在不考虑测量误差的情况下，对20 个矿区地表移动延续时间实测值和预测值的均方根误差(ERMS)[23]进行分析，计算公式为

误差计算结果表明：“三下开采指南”预测值和实测值的均方根误差高达882 d，Knothe 时间模型预测值和实测值的均方根误差为152 d，而本文建立的地表移动延续时间模型预测值和实测值的均方根误差仅为64 d，低于“三下开采指南”预测模型和Knothe时间模型，预计精度可以满足现场工程应用的要求。误差分析进一步证实了本文所建立的地表移动延续时间预测模型的精确性和合理性。

5 影响因素分析

5.1 煤层采高

由式(23)可知，地表移动延续时间主要受煤层采高、平均采深和煤层开采速度影响，分析各参数对地表移动延续时间的影响规律，对不同工程地质条件和开采强度下地表移动稳定状态评价具有重要的理论指导意义。假设煤层开采速度为3 m/d，下沉系数q为0.8，平均采深为500 m，计算水平煤层开采条件下，采高分别为2.0、2.5、3.0、…、6.0、6.5 和7.0 m 时地表移动延续时间，结果如图7 所示。

图7 采高对地表移动延续时间的影响Fig.7 Influence of mining height on surface movement duration

由图7 可知，地表移动延续时间随煤层采高的增加而增加，且增加幅度逐渐减小。这是由于煤层采高越大，开采引起的地表移动变形越剧烈，恢复到稳定状态需要更多的时间，因此地表移动延续时间越久。当采高由2 m 增加至7 m 时，地表移动延续时间由415 d 增加至443 d，仅增加了28 d，可见煤层厚度的增加引起地表移动延续时间的增加幅度并不明显。

5.2 平均采深

假设煤层开采速度为3 m/d，采高为3 m，下沉系数为0.8，计算平均采深分别为200、250、300、…、600、650、700 m 时地表移动延续时间，结果如图8所示。

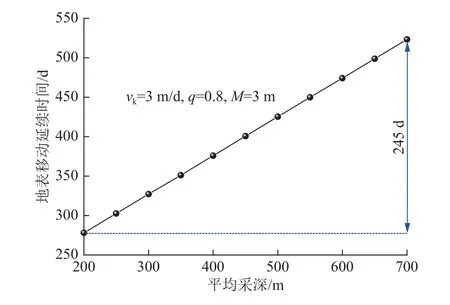
图8 平均采深对地表移动延续时间的影响Fig.8 Influence of mining depth on surface movement duration

由图8 可知，地表移动延续时间随煤层平均采深的增加而线性增加。这是由于煤层平均采深越大，开采引起的上覆岩层移动变形传递至地表需要更多的时间，地表从开始沉降至最终沉降稳定需要的时间也越多，因此地表移动延续时间越长。当平均采深由200 m 增加至700 m 时，地表移动延续时间由278 d增加至523 d，增加了245 d，增加幅度十分显著。但由于实际开采工程中，煤层开采深度已经确定，因此难以通过改变采深来控制地表移动延续时间。

5.3 煤层开采速度

假设煤层采高为3 m，下沉系数为0.8，平均采深为500 m，计算开采速度分别为2、3、4、…、10、11和12 m/d 时地表移动延续时间，结果如图9 所示。

图9 开采速度对地表移动延续时间的影响Fig.9 Influence of mining speed on surface movement duration

由图9 可知，地表移动延续时间随煤层开采速度的增加而非线性减小，并逐渐趋于平缓。这是由于煤层开采速度越大，工作面回采结束需要的时间越短，地表从开始沉降到最终沉降稳定需要的时间越少，因此地表移动延续时间越短。当开采速度由2 m/d 增加至5 m/d 时，地表移动延续时间由547 d 减小至291 d，减小了256 d，减小幅度十分显著；但当开采速度由5 m/d增加至12 m/d 时，地表移动延续时间由291 减小至226 d，仅减小了65 d，减小幅度不明显。因此，在实际开采过程中，当开采速度小于5 m/d 时，可通过适当加快煤层开采速度来缩短地表移动延续的时间，但当开采速度超过5 m/d 时，通过加快煤层开采速度来缩短地表移动延续时间的效果并不明显。