勾股定理：几何学中的一颗明珠

朱月红

同学们听过“大禹治水”的故事吗？他是如何成功治水的呢？赵爽在《周髀算经注》中这样写道：“禹治洪水，决流江河，望山川之形，定高下之势，除滔天之灾，释昏垫之厄，使东注于海，而无浸溺。乃勾股之所由生也。”大禹治水竟然与勾股定理有关，是不是很出人意料？在本章中，我们将一起领略几何学中的一颗璀璨明珠——勾股定理。

一、读史明智，寻“勾股定理”的雏形

在中国古代，人们把手臂弯曲成直角时，靠近肩膀的那部分叫作“勾”，靠近手掌的那部分叫作“股”。一般地，“勾”的长度小于“股”的长度。西周初年，商高在与周公旦的对话中提到“勾广三，股修四，径隅五”。后人称之为“勾三股四弦五”，这便是“勾股定理”的雏形。

对于32+42=52，这是勾股定理的一个特例，也是勾股定理在中国的最早记载。追根溯源，勾股定理是我国古代数学发展的重要起源，中华数学传统文化中的精髓开方术、方程术等都与勾股定理密切相关（有兴趣的同学可查阅《周髀算经》）。勾股定理的发现是一件不容易的事，勾股定理的证明更是一件了不起的事。千百年来，人们被它的魅力所吸引，对勾股定理的证明兴趣浓郁。目前，它是世界上已知证明方法最多的数学定理之一。

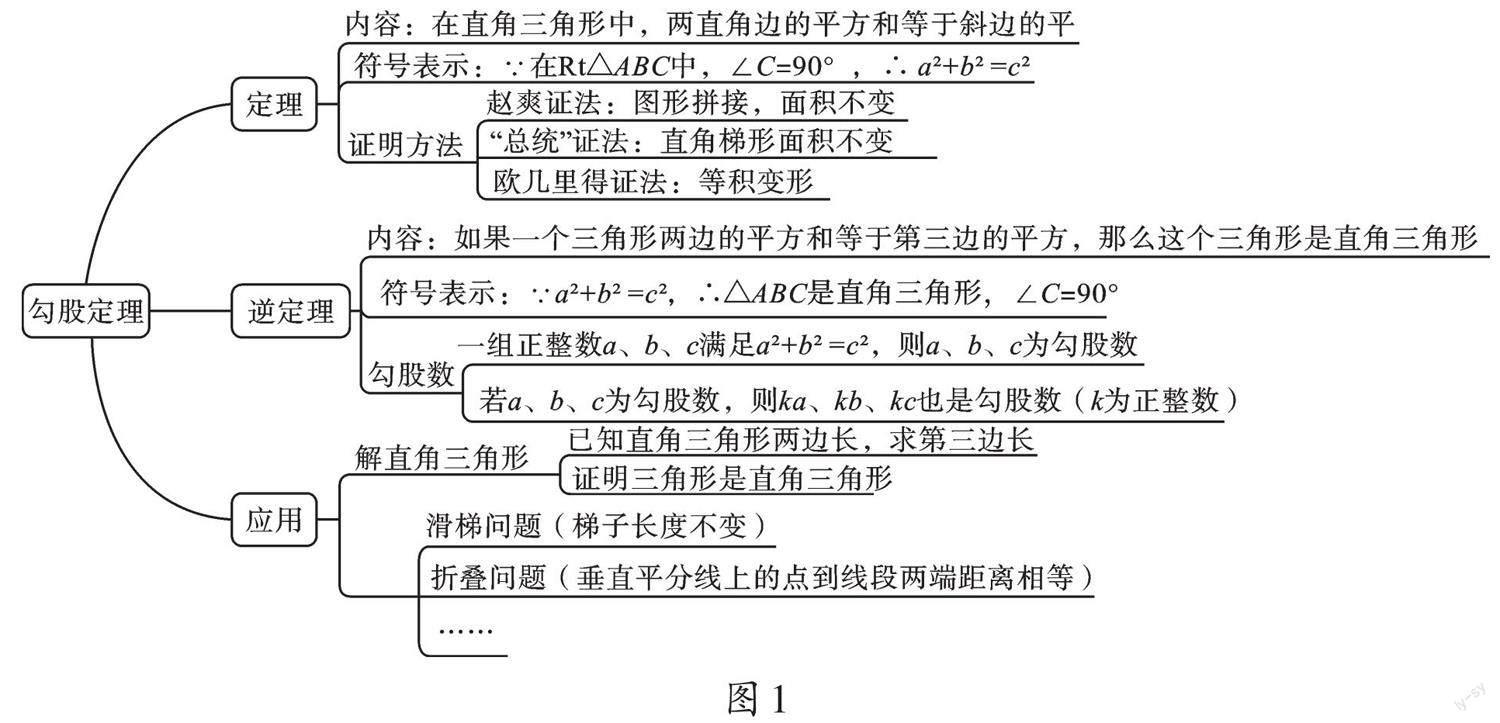
二、穿越古今，探“勾股定理”的结构

我们知道，三角形有六个元素（三條边和三个角），研究三角形就是研究各元素之间的关系。我们往往遵循从一般到特殊的规律，将一般三角形的边特殊化就是等腰三角形，角特殊化就是直角三角形。本章从生活中提炼直角三角形模型→画图归纳与验证勾股定理（边边关系）→图形变换理解勾股定理的判定方法→回归生活，运用勾股定理解决问题。具体说来，我们将建立如图1所示的知识结构，这也体现了本章的结构美。

三、学以致用，赏“勾股定理”的魅力

勾股定理在生活中有着极其广泛的应用，在中考试题中也大放异彩。例如，一架云梯AB长25m，如图2靠在墙上，云梯底端离墙7m。（1）如果云梯的顶端下滑了4m，则云梯底部在水平方向滑了多少米？（2）若云梯从起始位置图3到图4，上端下滑了a，下端水平滑了b，则a、b有什么关系？（3）点A与点B在滑动过程中，你还能发现什么问题？请你去探究。

分析：我们将实际问题转化成数学模型后，运用勾股定理列出方程即可。（1）设水平方向滑了xm，由勾股定理得OA=24，∴OA′=20。再由勾股定理得（7+x）2+202=252，得x1=8，x2=-22（舍去）；（2）由勾股定理得（25-a）2+b2=252，解得a2-50a+b2=0；（3）问题：在滑行的过程中，a=b吗？探究：若a=b，代入a2-50a+b2=0，得a1=0，a2=25，所以当a=0或25时，a=b，即云梯在起始时和最终平放地面上时a=b，滑行的过程中a≠b。

勾股定理作为一条古老的数学定理，包含着中国古代厚重的文明，它的出现和发展对发扬古代数学文化起到了重要作用。同学们，让我们一起走近“勾股定理”，感受它丰富的内涵吧！

［作者单位：江苏省泰州医药高新区（高港区）教师发展中心］