分析数据，用数据说话

2023-12-11时晓霞

初中生世界·九年级 2023年11期

关键词：仪仗队平均数方差

时晓霞

生活离不开数据。我们不仅要收集、整理和描述数据，还要分析数据，进而应用数据更好地作出判断。我们一般从“集中趋势”和“离散程度”兩个角度分析一组数据，其中常用平均数、中位数和众数刻画数据的集中趋势，用极差和方差表达数据的离散程度。

一、联系生活实际，引发问题

在表示一组数据集中趋势的统计量中，平均数是一组数据的“核心”，是刻画一组数据集中趋势时常用的统计量。我们先从生活中的一个问题开始说起。

例1 学校召开运动会，要组建一支仪仗队，从A班学生中挑选一组学生组成方队，他们的身高（单位：cm）如下：166，171，170，165，165，169，170，165，166，168，计算该组同学的平均身高。

【解析】一组数据平均数的基本算法是：[x]=[166+171+…+16810]=167.5（cm），我们称之为“算术平均数”。观察发现，这组数据在165～171之间，我们还可以这样考虑：先将各数据同时减去165（不妨称165为“基数”），得到一组新的数据1，6，5，0，0，4，5，0，1，3，计算这组新数据的平均数[x']=[1+6+…+310]=2.5（cm），然后加上165，可得平均身高为167.5cm。

当一组数据中的数较大，且都接近于某个数时，可将各个数据同时减去这个数，转化为计算一组新数据的平均数，体现“转化”思想。在确定“基数”的过程中，培养了观察、分析问题的能力。因此，学习是不断积累基本活动经验的过程。

二、积累生活经验，自我建构

仔细观察上述数据，165、166、168、169、170、171分别出现的次数是3次、2次、1次、1次、2次、1次，出现次数越多的数，表明它在这组数据中“越重要”——“权”越大，平均身高还可以这样算：[x]=（165×3+166×2+…+171×1）÷（3+2+…+1）=167.5（cm）。

表达一个数据的重要程度除了用出现的次数“权”来表达之外，也可以用比例（百分比）来表达。

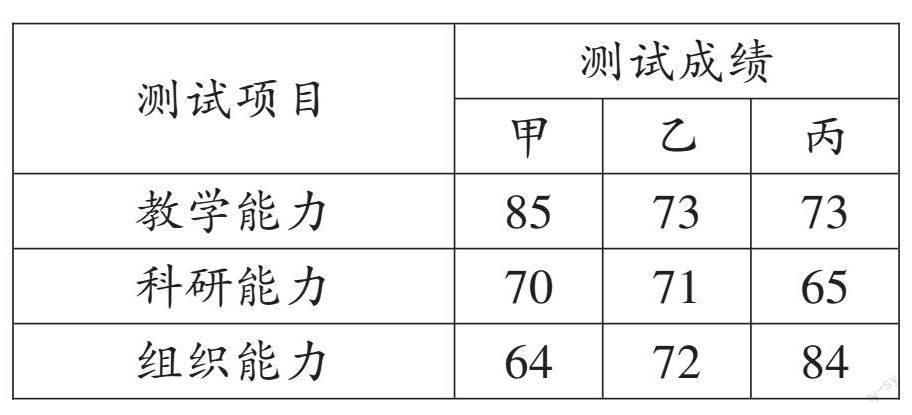
例2 某校欲招聘一名数学教师，学校对甲、乙、丙三位候选人进行了三项能力测试，各项测试成绩满分均为100分，根据结果择优录用。三位候选人的各项测试成绩如下表：

[测试项目测试成绩甲乙丙教学能力 85 73 73 科研能力 70 71 65 组织能力 64 72 84 ]

根据实际需要，学校将教学、科研和组织三项能力测试得分按5∶3∶2的比例确定每人的成绩，谁将被录用？

【解析】5、3、2表达了对应项的重要程度，即对应得分的“权”。[x]甲=[85×5+70×3+64×25+3+2]=76.3（分），同理，[x]乙=72.2（分），[x]丙72.8（分），则甲将被录用。

变式若学校比较注重组织能力，将教学、科研和组织三项能力的测试得分按3：2：5的比例确定每人的成绩，谁又将被录用？大家快去试试吧！

至此，我们可以体验到“加权平均数”与日常生活的密切联系，感受数学的应用性。

三、应用生活现实，体现价值

回到学校挑选仪仗队问题。