基于广义线性多面体的有源配电网仿射可调鲁棒优化方法
2023-12-11郎红科廖小兵
乐 健,郎红科,廖小兵,王 靖,毛 涛
(1.武汉大学电气与自动化学院,湖北省武汉市 430072;2.武汉工程大学电气信息学院,湖北省武汉市 430205;3.武汉亿磁源电力科技有限公司,湖北省武汉市 430223)
0 引言
中国为了实现“碳达峰·碳中和”这一国家重要战略目标,能源形态将从高碳排放的化石能源向低碳或无碳排放的新能源转变[1]。但是,随着新能源大规模发展和高比例接入,其波动性和随机性使得电网运行面临着随机扰动的风险[2]。传统配电网将逐步向供需互动的有源配电网升级,使得配电网的运行方式更加多样化[3]。如何有效克服新能源的不确定性、保证配电网安全经济运行成为目前亟须解决的难题。
为了处理分布式光伏出力的不确定性问题,配电网不确定性优化方法主要分为随机优化方法[4-6]和鲁棒优化方法。其中,基于场景法的随机优化方法虽然建模较为简单,但其生成的离散场景往往规模巨大且求解时间较长,导致求解效率低下。基于机会约束法的随机优化方法允许决策变量不满足约束条件,但其决策变量满足约束条件的概率需不低于事先设定的置信水平,且其必须假定随机变量服从某种概率分布,但在实际应用中通常存在缺乏历史数据和风电、光伏之间出力相关性不明确等问题,从而使得这种假定不一定成立或者与实际概率分布之间存在较大偏差。鲁棒优化方法通常采用不确定集合来描述分布式光伏的不确定性,因其无须获取分布式光伏出力的概率分布,且避免了大量场景导致的维数灾问题而受到越来越多的关注。
不同的不确定集合对鲁棒优化结果的影响显著。当不确定集合越精细时,模型复杂度越高、求解越困难;当不确定集合越宽泛时,所求出的最优解越保守、越不经济[7]。文献[8]采用区间不确定集合描述光伏、风电和负荷的不确定性,构建了考虑分布式电源辅助服务的两阶段混合整数二阶锥鲁棒优化模型,在列与约束生成的基础上提出一种新的两阶段直接交替迭代求解方法。文献[9]采用基于鲁棒成本的可调节鲁棒优化方法处理新能源出力不确定性,构建了主动配电网鲁棒优化经济调度模型。文献[10]以综合配置成本最小为目标函数,考虑风电和光伏出力的区间分布,提出一种基于鲁棒优化理论的主动配电网优化配置模型。文献[11]提出了考虑需求侧响应的配电网鲁棒优化模型,采用凸优化方法对模型中的不确定性问题进行求解。文献[8-11]均采用区间不确定集合来描述有源配电网中的不确定性变量,对于一些模型可能会出现所有不确定性变量都在区间集合上下界进行优化的情况,但现实中该情况发生的概率极低甚至不会发生,故很容易出现求解过度保守的问题。
多面体集合可以通过控制不确定度来确定不确定集合的包络范围,从而控制优化结果的保守性[12]。文献[13]基于风机、光伏出力与负荷的多面体不确定集合,提出了交直流混合配电网重构与无功优化协同的两阶段鲁棒优化模型。文献[14]采用时间、空间及功率区间三维多面体不确定集合描述电动汽车功率需求及可再生能源出力的不确定性,提出了电动汽车并网的分布式鲁棒优化模型。文献[15]采用多面体不确定集合描述风电和光伏出力的不确定性,通过设置不确定度来协调决策的鲁棒性和最优性,提出了计及分布式风力发电和光伏发电不确定性的三相配电网可调鲁棒无功优化模型。文献[13-15]采用多面体不确定集合来描述配电网中的不确定性变量,与区间集合相比可以减小优化结果的保守性,但这两种不确定集合都未考虑不确定性变量之间的相关性,导致决策的保守性还有待改进。
进一步,为在配电网优化调度中考虑不确定性变量之间的相关性,文献[16]采用椭球不确定集合描述风电功率的时空相关特性,将所建立的不确定性模型转化为混合整数二阶锥规划模型进行求解。文献[17]构建了源荷储协同运行优化模型,并采用椭球不确定集合描述分布式光伏出力的不确定性,提出了基于仿射可调鲁棒优化的主动配电网运行策略。虽然椭球不确定集合能够较好地考虑不确定参数之间的相关性,但其具有非线性结构,会增加问题求解的复杂度。为此,文献[18]采用椭圆不确定集合得到风电时间相关性轴线和中心点,形成风电时间相关性多面体不确定集合,提出了一种新的鲁棒机组组合模型。文献[19]提出一种基于广义凸包不确定集合的数据驱动鲁棒机组组合方法,广义凸包既能表示风电出力的相关性,又是线性形式,不会增加求解复杂度。但是,文献[18-19]的相关性不确定集合都是在椭球不确定集合基础上进行的改进,通过椭球顶点或者轴线连接形成新的集合:一方面,可能会导致不确定集合的包络范围减小,从而不足以包含所有的波动;另一方面,可能会导致不确定集合的包络范围增大,从而使决策的保守性增大。
基于上述研究,本文提出了基于广义线性多面体集合的有源配电网仿射可调鲁棒优化方法。与以往研究中采用椭圆不确定集合表示不确定参数相关性不同,首先,本文采用多面体不确定集合描述分布式光伏出力不确定性,其具有线性结构且易于控制不确定度,在实际工程问题中备受关注。然后,在传统多面体集合的基础上,通过分布式光伏出力的相关性分布包络图重构了多面体不确定集合的边界,进一步针对相关性多面体不确定集合存在的保守性偏大问题,建立了广义线性多面体不确定集合来描述分布式光伏出力相关性。最后,通过两个算例系统验证了本文所提出的广义线性多面体集合的有效性。
1 分布式光伏出力相关性多面体模型
1.1 光伏出力相关性多面体集合
采用多面体集合来描述分布式光伏出力的不确定性,如式(1)所示。
式中:ΩPolyhedral为分布式光伏出力的多面体集合;ZPolyhedral为分布式光伏出力的不确定因子集合;、P和分 别 为t时 刻 节 点j上 所 连 接 的 分 布 式 光伏的有功出力、出力期望值和出力波动最大值;zj,t为t时刻节点j上所连接的分布式光伏出力的不确定因子;Γ为多面体集合不确定度。
为分析方便,令ρ为分布式光伏出力之间的相关性系数,取两个不确定参数z1和z2来确定一个多面体不确定集合,如图1 所示。本节假设分布式光伏出力的相关性矩阵可以利用分布式光伏出力的历史数据得出。分别以不同的ρ对z1和z2进行随机采样,得 到z1和z1的 相 关 性 分 布 包 络 图[20]如 图2所示。
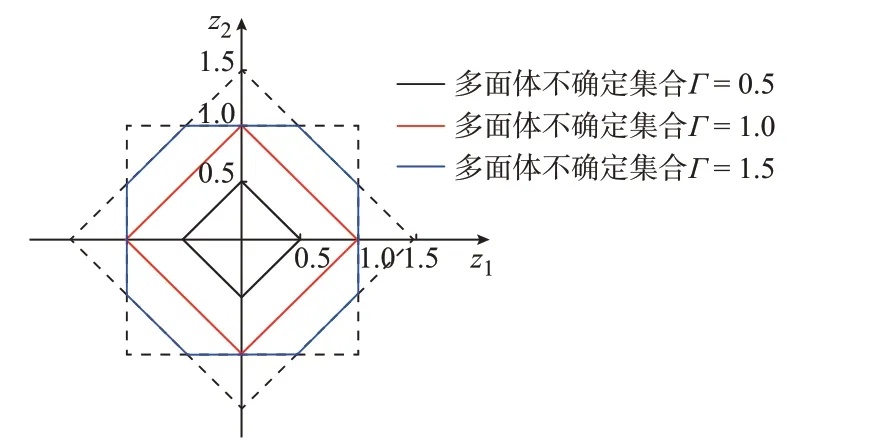
图1 不确定度对多面体不确定集合的影响Fig.1 Effect of uncertainty on polyhedral uncertainty set
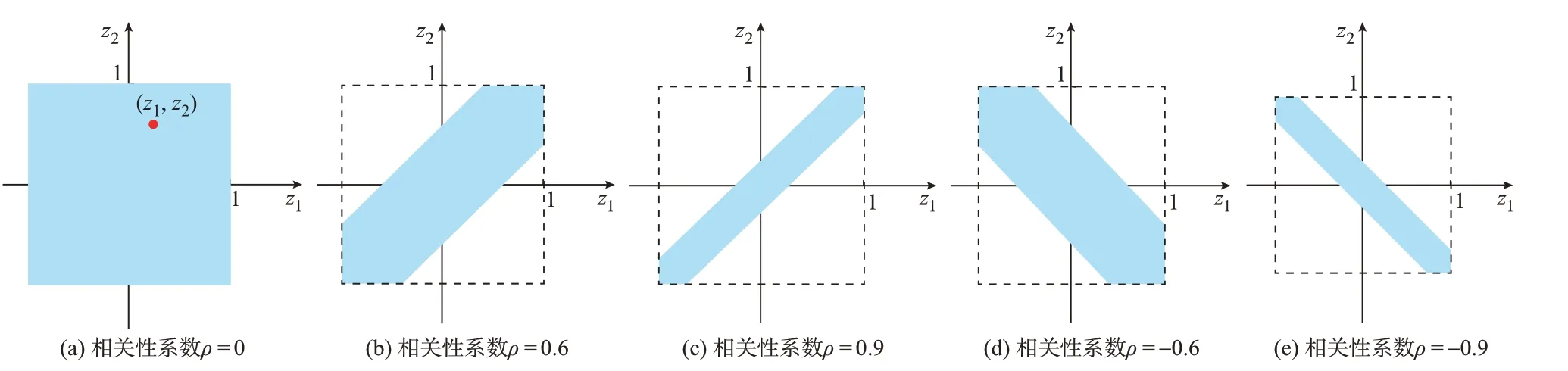
图2 不确定参数相关性分布包络图Fig.2 Correlation distribution envelope of uncertainty parameters
由图2 可以看出,当分布式光伏出力之间没有相关性时,由于|zj,t|≤1,分布式光伏出力的不确定参数分布形成了一个边长为1 的正方形区域。当相关性正向增加或负向减少时,不确定参数分别集中在直线y=x或直线y=-x周围。
由于分布式光伏出力之间存在相关性,分布式光伏出力波动采样点聚集在不确定参数的相关性分布包络图的对角线周围。因此,可以通过弯曲多面体的边界,使对角线周围区域覆盖的分布式光伏出力波动采样点比远离对角线区域覆盖得更多。这种重新构造的多面体不确定集合可以让分布式光伏出力的不确定参数更多地集中在对角线周围,而无须增加不确定度Γ去覆盖分布式光伏出力波动发生概率小的空白区域,具体如图3 所示。当分布式光伏出力的相关性系数越大时,多面体不确定集合的边界应该弯曲得更多。因此,重新构建的多面体不确定集合的形状取决于分布式光伏出力之间的相关性强弱,即相关性多面体不确定集合。

图3 相关性多面体不确定集合与多面体不确定集合Fig.3 Correlation polyhedral uncertainty set and polyhedral uncertainty set
光伏出力相关性多面体集合的数学表达式如式(2)所示,具体推导过程在附录A 中给出。
式 中:ρjk,t为 不 确 定 参 数zj,t和zk,t之 间 的 相 关 性 系数,ρjk,t∈[-1,1];n为分布式光伏的个数。
1.2 光伏出力相关性的广义线性多面体集合
虽然1.1 节提出的分布式光伏出力的相关性多面体不确定集合考虑了分布式光伏出力之间的相关性,但其包络的范围存在一定的缺陷。以直角坐标系的第一象限为例,具体如图4 所示。一方面,相关性多面体不确定集合只包络了不确定参数的相关性分布包络图的对角线周围的一部分区域,没有包络分布式光伏出力波动发生概率高的部分[21],如图4中绿色区域所示,这种情况会降低优化结果的鲁棒性;另一方面,其包络分布式光伏出力波动发生概率低的部分的比例仍然偏高,如图4 中相关性多面体不确定集合边界内的空白区域所示,这种情况会增大优化结果的保守性。
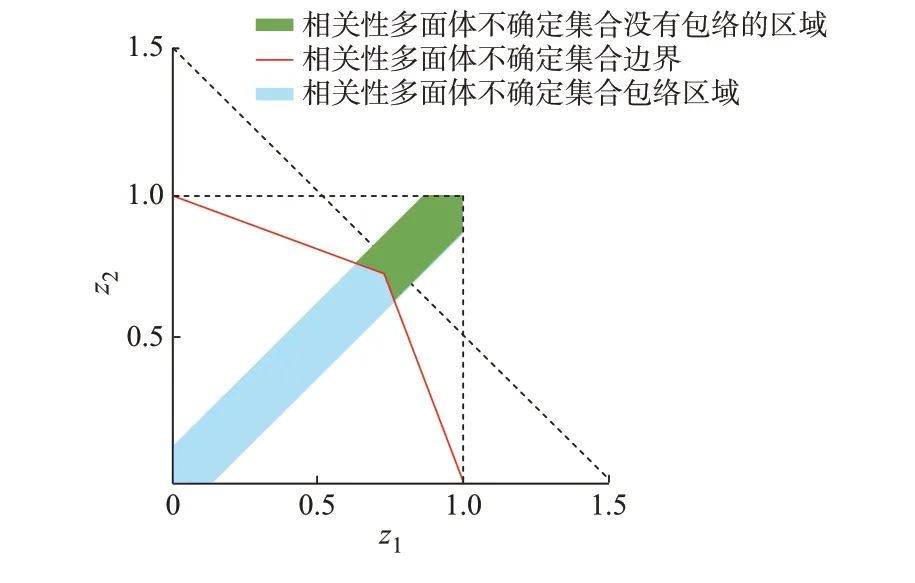
图4 相关性多面体不确定集合的包络范围Fig.4 Envelope range of correlation polyhedral uncertainty set
为进一步解决上述相关性多面体不确定集合的鲁棒性差和保守性大的问题,本节将对上述相关性多面体不确定集合进行改进,使其包络的空白区域的比例减少,包络对角线周围区域的比例增多,具体方法如附录B 图B1 所示。令不确定参数z1和z2形成的相关性分布包络图与直线y=1 相交的点中横坐标最小的点为H1(xH,1);同理,相关性分布包络图与直线x=1 相交的点中纵坐标最小的点为H2(1,yH)。令相关性分布包络图与y轴相交的点中纵坐标最大的点为D1(0,yD);同理,相关性分布包络图与x轴相交的点中横坐标最大的点为D2(xD,0)。当 点R1在 点D1和 点P1(0,Γ)之 间 波动,点R2在点D2和点P3(Γ,0)之间波动时,由点R1、R2、H1和H2构成的集合即为广义线性多面体集合。
从附录B 图B1 可以看出,广义线性多面体集合包络了不确定参数z1和z2形成的相关性分布图的所有区域,增大了优化结果的鲁棒性。当点R1越趋近于点D1、点R2越趋近于点D2时,改进的相关性多面体不确定集合所包络的空白区域越少,降低了优化结果的保守性。
在相关性系数确定的情况下,可以通过调整点R1和点R2的位置来控制线段Lc1和线段Lc2的包络范围,从而控制优化结果的保守性,如附录B 图B2所示。
光伏出力广义相关性多面体集合数学表达式如式(3)所示,具体推导过程在附录C 中给出。
式中:βc为控制线段和线段位置的参数,βc∈[0,1]。
2 有源配电网经济调度模型
2.1 有源配电网综合成本目标函数
本文考虑网损成本、购电成本、弃光惩罚成本以及电池储能系统(battery energy storage system,BESS)循环寿命日折损成本来构造主动配电网优化目标函数F,如式(4)所示。
式中:closs、c和cPV分别为网损成本系数、主网购电成本系数和弃光惩罚成本系数;rij为支路ij的电阻;Iij,t为t时 刻 支 路ij的 电 流;P为 节 点j处 关 口 在t时刻向主网的购电有功功率;CESS为BESS 循环寿命日折损成本;ΩL为线路集合;ΩTR为配电变压器关口节 点 集 合;T为 调 度 运 行 时 段 数;为t时 刻 节 点j上所连接的分布式光伏的预测功率值;ΩPV为分布式光伏接入节点集合。
2.2 有源配电网运行约束
1)二阶锥松弛潮流约束:
式中:u(j)为配电网中以j为末端节点的支路的首端节点集合;v(j)为配电网中以j为首端节点的支路 的末 端 节 点 集合;Vi,t=U,Ui,t为节 点i在t时 刻的 电 压 幅 值;Pij,t和Qij,t分 别 为 支 路ij在t时 刻 的 有功 和 无 功 功 率;lij,t=I;Pj,t和Qj,t分 别 为 节 点j注入 的 有 功 和 无 功 功 率;P和P分 别 为 节 点j处BESS 在t时刻的充电、放电功率;P、Q分别为节点j处负荷在t时刻的有功和无功功率需求;Q为t时刻节点j处关口向主网注入的无功功率;Q为t时刻节点j上所连接的分布式光伏的无功功率;Q和Q分别为t时刻节点j上所连接的静止无功补偿器(SVC)连续补偿功率、分组投切电容器组(CB)的离散补偿功率;xij为支路ij的电抗。
2)节点电压和支路电流约束:
式 中:Uj,max和Uj,min分 别 为 节 点j的 电 压 幅 值 上、下限;Iij,max为 支 路ij电 流 幅 值 上 限。
3)分布式光伏运行约束:
式中:S为节点j上所连接的分布式光伏逆变器的视在功率;θj为节点j上所连接的分布式光伏逆变器的功率因数角。
4)考虑循环寿命折损的BESS 运行约束
(1)BESS 循环寿命日折损成本
BESS 循环寿命日折损成本CESS主要是指一天内的充放电过程对循环寿命的折损所造成的损耗成本,这里BESS 全寿命周期成本按365 d 折算到每日。BESS 的全寿命周期成本主要由BESS 及其辅助设备的投资成本构成,由BESS 的额定容量和额定功率决定,即
式(12)为幂函数,本文根据文献[17]对BESS循环寿命日折损成本CESS进一步线性化得到:
式中:N为电池在一天中基于不同放电深度的等效循环次数;、和、分别为各次项线性拟合系数。
(2)BESS 运行约束
BESS 在运行过程中还受到充放电速率约束、能量平衡约束和充放电过程约束等,分别可表示为:
式中:S为节点j处BESS 在t时刻的荷电状态;ηch,j和ηdis,j分别为节点j处BESS 的充电、放电 效率;Δt为调度时间间隔;和分别为节点j处BESS的荷电状态上、下限。
5)CB 运行约束
CB 是一个离散的无功补偿的机械设备,需要限制其频繁动作次数,以延长使用寿命。具体约束为:
式 中:N为 节 点j上 所 连 接 的CB 在t时 刻 投 运 组数,是一个整数变量;Q,step为节点j上所连接的CB在t时刻每一组的补偿功率;B为一天T个周期内CB 的动作次数限制;N为节点j上所连接的CB 在t时刻投运的最大组数。
6)SVC 运行约束
进一步,考虑连续调节的无功补偿装置SVC,其运行约束为:
b.Shefelt a flood of relief.(Halliday&Matthiessen 1999:232)
式 中:Q和Q分别为节点j上 所连接的SVC 可调无功功率的下限和上限值。
7)配电网关口功率约束
为抑制配电网功率波动对主网造成的影响,需要将配电网关口功率控制在某一范围内,即
式 中:Pj,max和Pj,min分 别 为 配 电 网 节 点j处 关 口 有 功功 率 的 上、下 限;Qj,max和Qj,min分 别 为 配 电 网 节 点j处关口无功功率的上、下限。
8)有载调压变压器(OLTC)运行约束
在节点i和节点j之间添加了一个OLTC,增设一个辅助节点o,OLTC 运行有如下约束:
式 中:Vo,t为 辅 助 节 点o在t时 刻 的 电 压 幅 值 平 方;Nij,t为支路ij变压器在t时刻的优化挡位,是一个整数变量;Δkij为支路ij变压器分接头每一挡的增量;kij,t为 支 路ij变 压 器 在t时 刻 的 变 比;Kij为 支 路ij变压 器 分 接 头 的 挡 位 数;kij,max和kij,min分 别 为 支 路ij变压器变比的上、下限。
3 有源配电网的仿射可调鲁棒调度方法
3.1 有源配电网的仿射可调鲁棒调度模型
传统的有源配电网可调鲁棒优化模型中,根据决策变量的可调决策变量和不可调决策变量进行划分:不可调决策变量无论不确定性变量如何变化,都无法随之改变,故不可调决策变量是在不确定性变量实现前就已经确定;而可调决策变量依据不确定性变量的集合并随着不确定性变量进行调整。因此,从本质上来说,传统的有源配电网可调鲁棒优化模型是一个两阶段优化模型,需要迭代求解。
为此,本文提出了有源配电网仿射可调鲁棒优化(affinely adjustable robust optimization,AARO)[22-23]模型。AARO 模型采用线性仿射机制建立可调决策变量与不确定性变量之间的关系,这样可调决策变量根据线性仿射规则在可调范围内进行调整,而不再是在整个可调范围内进行无规则的决策。因此,本文的AARO 运行模型建立了配电网中的可调决策变量y与分布式光伏有功出力不确定性变量zj,t之间的线性仿射关系,以减小寻优盲目性,如式(28)所示。
式中:y为可调决策变量在初始时刻的值;ζj,t为仿射比例系数。
配电网AARO 运行模型相当于在传统的配电网可调鲁棒优化模型的基础上,增加了仿射线性决策机制,即对不确定集合中的任意不确定性变量,上述约束都成立,这简化了模型结构。
下文中,小写粗体字母表示列向量,大写粗体字母表示矩阵。依据第2 章建立的配电网优化模型和式(28)的线性仿射策略,得到配电网AARO 运行模型的向量形式如式(29)所示。
式中:x为不可调整的决策变量,是在不确定性变量获 取 之 前 的 一 次 决 策 变 量,Qij,t,lij,t,Vi,t];yc为 可 调 整 的 决 策 变 量,是 在 不 确 定性变量获取之后实时性改变的决策变量,yc=c1和c2分 别 为目标函数式(4)对应的系数矩阵;R、Ac、Bc、Dc、G、Cc、g分别为对应约束下变量的系数矩阵;r、hc、wc为 常 数 列 向 量;z为 由zj,t组 成 的 向 量。
式(29)中约束条件的第1 行约束条件表示仅与x有关的约束条件,包括BESS 运行约束、二阶锥潮流模型中的支路功率平衡约束和电压降落约束、节点电压和支路电流约束、OLTC 运行约束;式(29)中约束条件的第2 行约束条件表示二阶锥潮流模型中的二阶锥松弛约束;式(29)中约束条件的第3 行约束条件表示x与y有关的耦合约束条件,二阶锥潮流模型中的节点注入功率平衡约束;式(29)中约束条件的第4 行约束条件表示仅与y有关的约束条件,包括SVC 运行约束、关口功率约束和BESS 运行约束。
3.2 求解方法
式(29)中约束条件的第3 行约束条件包含不确定性变量z。对于zj,t∈ZPolyhedral,该不等式约束是鲁棒的,当且仅当其鲁棒对等约束成立[24-25],即
当ZPolyhedral为多面体不确定集合时,式(30)中的最大化问题可以等价为:
采用对偶理论,可得到式(31)的鲁棒对等问题为:
由式(33)可知,通过鲁棒对等将式(30)中含不确定性变量的max 项约束条件转换为相应的确定性min 项约束,可以与目标函数的min 项整合为统一形式。因此,基于多面体不确定集合的主动配电网AARO 模型就转化成确定性的混合整数二阶锥规划模型,可以直接调用商业求解器Gurobi 求解。
当ZPolyhedral为相关性多面体不确定集合和广义线性多面体集合时,同样可以通过鲁棒对等将不确定性约束转化为确定性约束。此处,以相关性多面体不确定集合为例进行说明,则式(30)中的最大化问题可以等价写成:
采用对偶理论,可得到式(34)的鲁棒对等问题为:
同理,通过鲁棒对等将式(30)中含不确定性变量的max 项约束条件转换为式(35)所示的确定性min 项约束,可以与目标函数的min 项整合为统一形式。
具体AARO 方法求解流程如图5 所示。

图5 AARO 方法求解流程图Fig.5 Solving flow chart of AARO method
4 算例分析
4.1 算例系统设置
为验证本文所采用的AARO 方法的有效性,本节通过改进的IEEE 33 节点和PG&E 69 节点两个测试系统进行算例分析。改进的IEEE 33 节点和PG&E 69 节点系统接线分别如附录B 图B3 和图B4所示。附录B 表B1—表B5 给出了接入两个系统的PV、BESS、CB、OLTC 的参数设置。系统基准电压为12.66 kV,基准容量为10 MV·A。IEEE 33 节点系统的关口有功功率取值为0~5 000 kW,无功功率取值为0~2 500 kvar;PG&E 69 节点系统的关口有功功率取值为0~7 000 kW,无功功率取值为0~5 000 kvar;IEEE 33 节点系统的支路电流幅值上限为0.4 p.u.;PG&E 69 节点系统的支路电流幅值上限为0.8 p.u.;节点电压幅值取值均为0.95~1.05 p.u.。
1)不确定度Γ对优化结果的影响
不确定度是用来限制多面体不确定集合中分布式光伏出力扰动范围的大小。从表1 可以看出,随着多面体不确定度Γ的增大,BESS 循环寿命日折损成本不变、网损成本逐渐增大、购电成本略微增大、弃光惩罚成本逐渐减小。这是因为多面体不确定度Γ的增大会导致光伏出力的波动范围增大,而过大的光伏出力导致配电网无法就地消纳。此时,需要将过剩的光伏功率输送到远离光伏电站的负荷节点消纳,导致支路电流增大,而为了功率达到平衡,关口功率需要略微增发,故网损成本增加、购电成本略微增大。随着不确定度Γ增大,调度方案保守性更强。因此,调度计划能更好地应对光伏波动,从而使得弃光量减小、弃光惩罚成本减小。而BESS 因其容量、充放电速率等约束难以响应分布式光伏的大范围波动,BESS 循环寿命日折损成本没有受到影响。

表1 不确定度Γ 对各项成本的影响Table 1 Impact of uncertainty Γ on various costs
2)相关性系数对优化结果的影响
相关性系数的大小会影响分布式光伏出力的相关性多面体不确定集合的边界的弯曲程度,从而影响相关性多面体不确定集合的包络范围,导致优化结果也会产生相应变化。如附录B 图B5 所示,当分布式光伏出力之间的相关性系数ρ分别为0.1 和0.4时,由于分布式光伏出力之间的相关性较弱,相关性多面体不确定集合的边界的弯曲程度较小,分布式光伏出力波动范围在多面体不确定集合和相关性多面体不确定集合下几乎没有变化,导致各项成本也几乎一致。当分布式光伏出力之间的相关性系数逐渐增大时,相关性多面体不确定集合的边界的弯曲程度逐渐增大,当ρ为0.9 时,相关性多面体不确定集合包络分布式光伏出力具有相关性的部分也较多。因此,分布式光伏出力增大,使得弃光电量减小、支路电流增大,导致弃光惩罚成本减小、网损成本增加。另一方面,由于分布式光伏出力相关性程度增大,相关性多面体不确定集合包络分布式光伏出力波动发生概率小的空白区域也增多,导致系统总成本增大,优化结果的保守性也相应增大。
表2 给出了3 种多面体不确定集合下的各项成本,取不确定度Γ=0.5,相关性系数ρ=0.9。可以看出,3 种多面体不确定集合中采用广义线性多面体集合的弃光成本和系统总成本最小,BESS 循环寿命日折损成本和购电成本不变。因为广义线性多面体集合包含了分布式光伏出力相关性分布图的全部范围,考虑了分布式光伏出力波动最大的情况,同时减小了分布式光伏出力波动发生概率小的空白区域。分布式光伏出力虽然增大,但绝大部分的光伏出力就地消纳,只有小部分的光伏出力被输送到其他负荷节点,此时,分布式光伏出力可满足配电网功率平衡。因此,弃光成本变小,BESS 循环寿命日折损成本和购电成本不变,系统总成本也随之变小。当βc增大时,分布式光伏出力波动发生概率低的空白区域增大,广义线性多面体集合的包络范围也随之增大,导致分布式光伏出力进一步增大,但此时绝大部分的光伏出力无法就地消纳,需要输送到其他负荷节点,导致在弃光成本减小的同时网损成本增大,系统总成本基本不变。基于以上分析,广义线性多面体集合包络了分布式光伏出力不确定参数形成的相关性分布图的所有区域,考虑了分布式光伏出力波动最大的情况,增大了优化结果的鲁棒性,且其包络分布式光伏出力波动发生概率较小的空白区域更少,降低了优化结果的保守性。

表2 3 种多面体集合对各项成本的影响Table 2 Impact of three polyhedral sets on various costs
为对比椭球不确定集合AARO 方法与广义线性多面体集合AARO 方法的优劣,附录B 表B6 对比了4 种不确定集合AARO 的各项成本。从表中可以看出,椭球不确定集合AARO 的各项成本最低,表明了椭球集合AARO 方法的保守性最小,但椭球不确定集合具有非线性结构,进行鲁棒对等时只能将含不确定参数的约束对偶为二阶锥约束,增加了问题求解的复杂度,求解时间也较长。虽然广义线性多面体集合AARO 的各项成本较椭球集合AARO 更高一点,但其既能刻画不确定参数间的相关性,又具有线性结构,求解时间也较短。
3)节点电压分析
附录B 图B6 给出了IEEE 33 节点系统中不确定度Γ=0.5,相关性参数ρ=0.9、βc=0.5 的情况下,采用3 类多面体集合得到的节点电压分布情况。可以看出,3 类多面体集合得到的节点电压分布均在0.95~1.05 p.u.的安全范围内,但在光伏出力较大的时段8 至13,考虑光伏相关性的多面体集合下的节点电压波动较小,并且广义线性多面体集合下的节点电压波动范围更小,主要集中在1.025 p.u.附近,进一步验证了广义线性多面体集合的保守性最小。
4)BESS 充放电功率分析
附录B 图B7 对比了在IEEE 33 节点系统中,采用3 类多面体集合得到的节点15 处BESS 充放电功率和SOC 分布情况,取不确定度Γ=0.5,相关性参数ρ=0.9、βc=0.5。从附录B 图B7 中的充放电功率曲线可以看出,在时段1 至6,分布式光伏出力为零,BESS 主要将初期存储的能量进行释放,以起到平移负荷的作用;在时段10 至14 的大部分,分布式光伏出力大发,BESS 进行充电存储能量。其中,在时段11 至12,考虑光伏出力相关性的改进多面体集合光伏出力最大,BESS 充电存储能量达到峰值,进一步说明改进的相关性多面体集合的光伏出力波动范围更紧凑,优化结果的保守性最小;在其他时段,分布式光伏出力和负荷需求都处于低位,BESS 达到容量之后不再进行充电过程。
4.2 PG&E 69 节点算例分析
表3 给出了在PG&E 69 节点系统中不确定度Γ对优化结果的影响。从表中可以看出,随着多面体不确定度Γ的增大,BESS 循环寿命日折损成本不变、网损成本逐渐增大、购电成本略微增大、弃光惩罚成本逐渐减小。PG&E 69 节点系统中的各项成本的变化规律与IEEE 33 节点系统中基本一致。
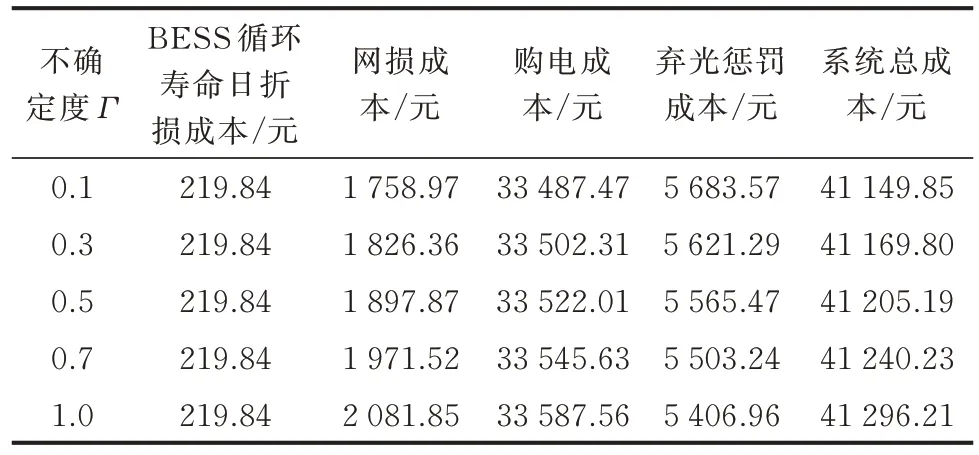
表3 PG&E 69 节点系统中不确定度Γ 对各项成本的影响Table 3 Impact of uncertainty Γ on various costs in PG&E 69-bus system
附录B 图B8 和表4 给出了在PG&E 69 节点系统中,相关性参数ρ和βc的大小对各项成本的影响。从附录B 图B8 和表4 可以看出,在PG&E 69 节点系统中,当分布式光伏出力之间的相关性较弱时,各项成本几乎一致;当分布式光伏出力之间的相关性系数逐渐增大时,弃光惩罚成本减小、网损成本增加、系统总成本增大。同时,广义线性多面体集合下的总成本最小。因此,PG&E 69 节点系统中各项成本的变化规律与IEEE 33 节点系统中基本一致,说明本文提出的广义线性多面体集合AARO 方法不仅适用于IEEE 33 节点算例的主动配电网小系统,而且适用于PG&E 69 节点算例的大系统。
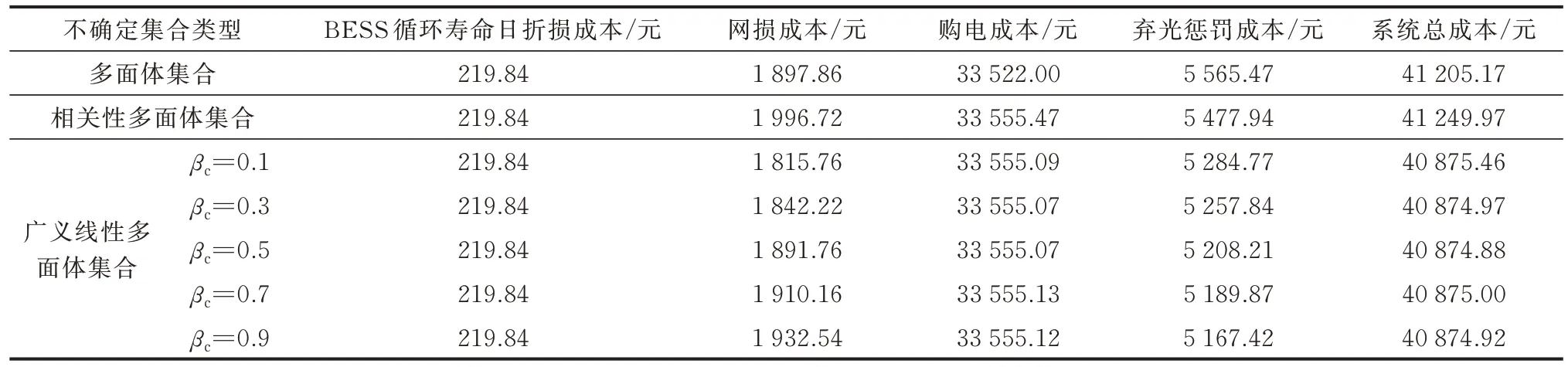
表4 PG&E 69 节点系统下3 种多面体集合对各项成本的影响Table 4 Impact of three polyhedral sets on various costs in PG&E 69-bus system
5 结语
本文构建了考虑分布式光伏相关性的有源配电网仿射可调鲁棒优化模型,通过对偶变换将其转换为一个确定性的混合整数二阶锥规划模型进行求解。算例结果表明:
1)在同样的不确定度下,与不考虑分布式光伏相关性的多面体不确定集合AARO 方法相比,相关性多面体不确定集合AARO 方法的弃光惩罚成本最小,但网损成本最大,且系统总成本增大,导致优化结果的保守性增大。
2)广义线性多面体集合既涵盖了光伏出力波动的全部范围,又减小了分布式光伏出力波动发生概率较低的空白区域。因此,广义线性多面体集合AARO 方法的弃光成本最低,并且网损成本相较于相关性多面体不确定集合AARO 方法更低,系统总成本最低,在一定程度上既增加了优化结果的鲁棒性,又降低了优化结果的保守性。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。
