基于改进型Stackelberg博弈的自动驾驶测试数据定价模型

涂辉招， 刘建泉， 遇泽洋， 李 浩， 郭新宇， 张韬略， 孙立军

（1. 同济大学 道路与交通工程教育部重点实验室，上海 201804；2. 同济大学 法学院，上海 200092）

我国“十四五”规划纲要指出，要加快数字化发展，促进数据交易流通，推动数字经济和实体经济深度融合，推进数字产业化。“数据二十条”［1］强调，要“支持探索多样化、符合数据要素特性的定价模式和价格形成机制，推动用于数字化发展的公共数据按政府指导定价有偿使用”。自动驾驶测试过程中产生的海量数据，蕴含高额潜在价值，但目前数据的交易流通进展却十分缓慢［2］。其主要原因之一是数据价值难以被估值［3］，亟需建立一套有效的数据定价方法，激发数据价值。数据定价方法是把数据作为资产并对资产进行定价的行为［4］。

数据是信息的载体，其使用过程带来的预期收益直接取决于数据中包含的信息量，因此数据信息量是数据价值评估的核心指标［5-6］。信息熵可以表征数据集包含的信息量［7-8］，是数据信息测量方法中最基本的概念。数据定价模型主要包括基于订阅［9-10］、基于查询［11-14］、基于数据质量［15-16］、基于拍卖［17-20］、基于博弈论［21-23］等模型。基于订阅的数据定价方法，根据特定企业之间达成的订阅协议，数据消费者通过支付订阅费，获取指定时间段内和订阅范围内的数据，适用于数据交易主体较少、数据消费者需求单一且长期稳定的情况。基于查询的数据定价模型依托SQL（structured query language）关系型数据库，数据生产者预先设置基本查询视图的数据价格，数据消费者按需进行数据查询并购买，查询结果由基本查询视图组合而成，但查询过程复杂度较高，且预先设置的视图难以完全覆盖自动驾驶测试过程中实时产生的大量数据，可操作性较低［24］。基于数据质量［15-16］的定价模型，通常利用效用函数等手段从数据质量和数据容量两方面来衡量数据价值。基于拍卖的数据定价模型［17-20］更多强调不同数据消费者之间的竞价过程。这4类模型难以对数据本身的真实价值进行深度挖掘［4］。Stackelberg 博弈模型是基于博弈论的经典定价模型，考虑了交易过程中决策的先后次序及数据本身对于数据消费者的使用价值，因此更能真实地描述交易决策过程及数据价值发现过程［15，25］。

但现有数据定价模型尚存在不足之处。首先，基于信息熵的数据信息量评估多以机器学习离散数据集为主，且数据集中通常仅包含直接信息特征［26］。自动驾驶测试数据集同时包含离散和连续变量，并且包含时间戳、经纬度等非重复且无法直接使用的间接信息特征。若采用传统信息熵方法评估，其计算结果与数据集尺度具有直接的函数关系，而与速度、驾驶模式等核心特征的分布无关。这就导致信息量评价结果难以体现自动驾驶特点，且与实际使用效果关联性较弱，缺乏合理性。其次，因为数据作为关乎国家安全的重要资源，现有基于Stackelberg博弈的数据定价模型中，大多设置多个数据生产者和消费者，但仅考虑一个垄断的数据平台，他们在决策过程中均追求自身效用的最大化［22，25］。但这样的模型假设会使得数据平台凭借其垄断地位，攫取过多数据生产者和消费者的利益，从而抑制数据市场的活力。此外，该模型缺乏对于数据信息量和数据交易博弈过程的全面考虑，未引入数据信息量评估数据价值，导致数据消费者效用缺乏合理性，且数据交易量不具有实际的物理单位，可操作性较低。

本文提出了考虑信息量和平台利润率约束的改进型Stackelberg 博弈自动驾驶测试数据定价模型，包含数据信息量评估以及数据定价两部分。在数据信息量评估环节，提出了基于特征工程的驾驶模式加权信息熵方法，对传统信息熵方法进行了适应性调整，包括特征的挖掘和过滤、连续变量离散化、驾驶模式加权等步骤。然后将评估所得信息量作为数据交易量的度量单位和数据价值评估的重要指标，进行数据的交易定价。在数据定价环节，构建了考虑信息量和平台利润率约束的改进型Stackelberg博弈数据定价模型。最后，基于上海市自动驾驶实际测试数据开展典型案例分析和模型验证。

1 定价模型

1.1 模型框架

图1 给出了基于改进型Stackelberg 博弈的数据定价模型整体框架。框架主要分为数据信息量评估、数据定价两个步骤。第一步数据信息量评估，主要采用基于特征工程的驾驶模式加权信息熵，包括：①基于特征工程挖掘潜在直接信息特征；②连续变量离散化，即过滤间接信息特征，并对每个连续变量信息等距分箱，以差分信息熵和分箱后离散信息熵最接近的原则确定最优分箱数；③计算自动驾驶驾驶模式加权信息熵。第二步数据定价，主要是考虑信息量和平台利润率约束的改进型Stackelberg博弈数据定价模型，其中数据交易量的度量单位是第一步所确定的数据信息量。

图1 基于改进型Stackelberg博弈的自动驾驶测试数据定价模型框架Fig. 1 Structure of autonomous vehicles testing data pricing model based on evolved Stackelberg game

1.2 基于特征工程的驾驶模式加权信息熵

1.2.1 传统信息熵

传统信息熵主要分为离散数据集信息熵、连续变量信息熵两类。

（1）离散数据集信息熵：对于有n条记录的离散数据集D，将每行记录视为一个向量，这些向量共有m个不同的取值{vi|i=1，…，m}，每个取值的概率为p(vi)，则数据集的信息熵Hd(D)定义为

式中：b为对数的基，当取值为2时，信息熵的度量单位为bit，后文默认取值为2。

（2）连续变量差分信息熵：对于有n条记录的变量V，共有m个不同的取值{vi|i=1，…，m}，其概率密度函数为f(vi)，则该变量的信息熵Hc(V)定义为

自动驾驶测试数据集中的时间戳不会重复，因此在有n条记录的自动驾驶测试数据集D中，将每行记录视为一个向量，这些向量有n个不同的取值，每个取值的概率为1n，代入式（1）中，可得到基于传统信息熵方法针对自动驾驶测试数据集的计算结果，即

从式（3）可以看出，计算所得信息熵和数据集尺度有直接的函数关系，和速度、加速度等表征自动驾驶特点的关键变量的分布无关。

1.2.2 驾驶模式加权信息熵

1.2.2.1 名词定义

直接信息特征：数据集中可被直接使用创造价值的特征，如自动驾驶测试数据集中速度、加速度、驾驶模式等。

间接信息特征：数据集中无法被直接使用，需要经过数据挖掘获取潜在的直接信息特征，才能被使用创造价值的特征，如自动驾驶测试数据集中的时间戳、经纬度等特征。

潜在直接信息特征：基于间接信息特性挖掘得到，可以直接被使用创造价值的特征，例如自动驾驶测试数据集中，基于时间戳挖掘得到的高峰/非高峰标签，以及基于经纬度挖掘得到的测试环境风险度等。

1.2.2.2 整体流程

（1）特征工程：首先进行潜在直接信息特征挖掘，梳理自动驾驶测试数据集中时间戳、经纬度等非直接信息特征，并根据数据使用者的需求，挖掘补充潜在直接信息特征，如高峰/非高峰标签、测试环境风险度等；然后进行特征筛选，仅考虑直接信息特征、潜在直接信息特征进行后续的信息熵计算。

（2）连续变量离散化：对于每个连续变量，基于式（2）计算其差分信息熵Hc，然后进行等距分箱，并基于式（1）计算分箱后的信息熵Hd，以分箱后Hd和Hc最接近的原则确定最优分箱数，把连续、离散变量混合数据集转化为离散数据集。

（3）基于驾驶模式加权信息熵计算方法，对分箱后的离散数据集进行信息熵计算。

1.2.2.3 驾驶模式加权信息熵

对于自动驾驶测试数据，其自动驾驶、人工驾驶模式下数据的价值有明显的差异，因此本文将驾驶模式权重wi引入到式（1）中，提出驾驶模式加权信息熵Hw(D)。

对于有n条记录的离散数据集D，将每行记录视为一个向量，这些向量共有m个不同的取值{vi|i=1，…，m}，每个取值的概率为p(vi)，对应的驾驶模式为di，则数据集的驾驶模式加权信息熵Hw(D)定义为

式中：w(di)为驾驶模式权重，自动、人工驾驶模式下的权重根据数据消费者的需求确定。

1.3 考虑信息量和平台利润率约束的改进型Stackelberg博弈数据定价模型

1.3.1 模型假设

（1）交易参与方：数据生产者、数据平台、数据消费者。其中数据生产者负责采集、存储测试数据，将原始数据出售给数据平台；数据平台根据数据消费者的需求进行数据加工，将加工后的数据出售给数据消费者；数据消费者从数据平台购买数据，并使用数据创造价值。考虑自动驾驶测试数据交易市场中仅存在一个垄断的数据交易平台的情形［22，27］。

（2）交易流程：①数据生产者进行原始定价；②数据平台确定分销价格；③对于给定的分销价格，结合自身的数据需求量，数据消费者确定其数据购买量（即信息量大小）；④数据平台从数据生产者购买相应信息量的数据，加工后出售给数据消费者。

（3）决策逻辑：数据所有者、数据平台、数据消费者均追求自身效用的最大化，其中数据平台受制于平台型经济的监管，其最大利润率会受到限制。

（4）数据量交易单位：数据信息量，使用基于特征工程的驾驶模式加权信息熵方法进行确定。

1.3.2 模型构建

1.3.2.1 数据生产者

式（5）～（7）中：U1为数据生产者的效用；x为自动驾驶测试数据集的信息量；po为自动驾驶测试数据的原始定价；cc为采集、存储、传输每bit 信息量的数据所花费的全部成本。

定义信息采集效率1/cc，可通过降低人工驾驶时长占比、丰富测试场景等方式提高信息采集效率，从而降低cc。数据生产者利润率R1为其利润除以数据的采集、存储、传输成本，计算方法如下：

1.3.2.2 数据平台的效用模型

式（9）～（12）中：U2为数据平台的效用；pd为加工后数据的分销价格；cp为数据平台加工、传输1 bit信息量数据的全部成本；β为数据平台的最大利润率水平。

数据平台利润率R2为其利润除以数据的加工、传输成本，计算方法如下：

结合式（12）和式（13），可得到R2≤β，即数据平台的利润率受到阈值β的约束。

1.3.2.3 数据消费者的效用模型

式（14）、（15）中：U3为数据消费者的效用；k为数据价值挖掘能力，和行业整体数据挖掘能力相关，不区分具体的数据消费者；ξ为数据价值系数，和数据质量、测试场景丰富度等数据集自身属性相关；d为数据消费者对数据信息量的需求量级，当量级为bit时取值为1，量级为byte时取值为8，量级为KB时取值为8×1 024，以此类推。

数据消费者利润率R3为其利润除以数据的购买成本，计算方法如下：

1.3.3 模型求解

采用后向归纳法求解上述3 层Stackelberg 博弈模型的平衡点［22］。首先分析数据消费者的决策模型，求解使得U3(x，pd)最大的数据购买量x。求U3(x，pd)对于x的偏导，即

当U3(x，pd)的二阶导小于0 时，x*是全局最优解，因此验证U3(x，pd)对于x的二阶导的正负性，即

将x*代入U3(x，pd)，可以得到

限制数据平台的利润率为β，则令U2(x*，pd，po)=βcpx，可以得到

求解式（11）可得，数据平台的最优定价为

将、x*代入式（5），可以得到

当U1(x*，po)的二阶导小于0 时，是全局最优解，因此对U1(x*，po)二阶导的正负性进行验证，即

显然小于0，因此可判断是使U1(x*，po)达到最大值的全局最优解。

因此可以得到上述Stackelberg博弈模型的平衡点如下：

2 典型案例分析

2.1 加权信息熵

2.1.1 自动驾驶测试数据来源

选取上海市2021 年1—3 月某自动驾驶车辆测试数据，数据量约5.1万条，其中自动驾驶模式数据约4.1 万条，数据字段包括车辆编号、经纬度、时间戳、速度、加速度、驾驶模式（自动驾驶/人工驾驶）等，时间颗粒度为1 s。

2.1.2 机器学习训练

为了在案例分析中验证数据信息量评估结果的有效性，对案例数据集进行了机器学习的训练。核心假设是根据大量机器学习经验，输入分类器的有效信息越多，分类器的分类准确率就越高［7］。如果基于特征工程的驾驶模式加权信息熵可以衡量数据集的有效信息量，那么驾驶模式加权信息熵与分类器对该数据集的准确率成正比。因此，本文从自动驾驶测试数据集中取出不同比例的数据行构建子数据集，使用子数据集训练4种常见的分类器，计算准确率的平均值，将所提出的基于特征工程的驾驶模式加权信息熵、传统信息熵和分类器准确率的平均值进行对比，从而验证模型的有效性。

分类器选取：选取机器学习中常用的决策树（DT）、Logistic回归（LR）、随机森林（RF）、支持向量机（SVM）在不同数据比例的子数据集进行有监督训练。

训练目标：自动驾驶测试数据的核心价值是体现自动驾驶的特征，在尽可能接近驾驶能力边界的条件下，暴露关键的测试问题，服务于风险的预测和管理，因此本文选取现阶段研究中最常见的脱离预测［28］，以及驾驶模式识别［29］，作为分类器的训练目标。

准确率验证方法：十折交叉验证法，即用10 次结果准确率的平均值作为对算法准确率的估计。

2.1.3 自动驾驶测试数据集信息量

潜在直接特征挖掘：基于时间戳补充高峰/非高峰特征，基于经纬度补充道路环境风险度特征。

驾驶模式权重：将自动驾驶模式权重设置为1，人工驾驶模式权重设置为0。

图2a 和2b 分别是脱离预测和驾驶模式识别的准确率训练结果，图2c是基于特征工程的驾驶模式加权信息熵和传统信息熵计算结果。可以看出，传统信息熵随着数据集尺度的增加单调递增，而基于特征工程的驾驶模式加权信息熵和上述两个分类器准确率的变化趋势更为接近，可以更合理地表征自动驾驶测试数据集的信息量。

图2 常用分类器准确率及对应信息熵Fig. 2 Accuracy of commonly used classifiers and corresponding information entropy

2.2 考虑平台利润约束的Stackelberg 博弈数据定价模型

2.2.1 对比模型

基础Stackelberg 博弈数据定价模型，不考虑数据消费者需求量，且不限制数据平台利润率［22］。

2.2.2 参数设置

基于合作车企的自动驾驶测试的实际测试情况估算，设置cc=100 元·bit-1。cp在cc的基础上乘以折减系数估算，约为cc的1/10，cp=10 元·bit-1。基于当前互联网平台型企业的利润率水平，设定β=50%。k和ξ是模型的拟合参数，需要基于自动驾驶测试数据的实际交易信息进行拟合确定。本文初步设置k=300（假设数据消费者针对1 bit信息量的数据，可获取采集成本3倍的效用），ξ=1（假设数据无额外价值系数）。本文通过分析参数变化对数据交易量、系统总效用、三方利润率的影响，展示改进型Stackelberg博弈数据定价模型的合理性。后续可随着自动驾驶测试数据实际信息的开展进一步校准。

2.2.3 数据消费者数据需求量级的影响

数据消费者的信息需求量级为byte、KB、MB、GB、TB 的情况，即d=[8， 8×210，8×220，8×230，8×240]。

从图3 可以看出，基础Stackelberg 博弈数据定价模型（图3b）无法反应数据消费者需求量级的影响，且交易数据量没有明确的物理单位，在实际操作中存在困难；而基于改进型Stackelberg 博弈的数据定价模型（图3a）可以较好地反应二者关系，且根据2.1节的分析，自动驾驶测试数据信息量和数据使用效果直接相关，且有明确的信息存储度量单位，在数据交易过程中更具有合理性和可行性。

图3 数据消费者数据需求量级对数据交易量的影响Fig. 3 Impact of data consumer demand on data transaction volume

后文的分析中包含了两个模型下数据交易量的对比，但基础Stackelberg 模型的数据交易量没有明确物理单位，两个模型不具有直接可比性，因此为了使对比更加直观，后文将基础Stackelberg 博弈数据定价模型中数据交易量的物理单位和基于改进型Stackelberg博弈的数据定价模型保持一致。

2.2.4 数据消费者数据价值挖掘能力的影响

分析数据消费者数据价值挖掘能力k提升的影响。设置k=[300， 325， 350， 375， 400，425，450，475， 500]。将数据消费者的数据需求量级d设置为1，其他参数保持不变。

图4a显示了数据消费者的数据价值挖掘能力对数据交易量的影响，可以看出，限制数据平台利润率后，可以明显提升市场中的数据交易量，从而大大激发数据市场活力；图4b显示了数据价值挖掘能力对系统总效用的影响，可以看出，限制数据平台利润率后，虽然数据平台的效用会受到一定程度上的限制，但因为数据交易量上升，系统总效用有明显的提升，表明基于改进型Stackelberg博弈的数据定价模型可以使数据生产者、消费者获取更多利益，从而鼓励数据的生产和交易。

图4 数据价值挖掘能力对数据交易量、系统总效用的影响Fig. 4 Impact of data value mining ability on data transaction volume and total system utility

图5显示了基于改进型Stackelberg 博弈（图5a）和基础Stackelberg博弈（图5b）的两个数据定价模型下数据消费者的数据价值挖掘能力提升对交易三方利润率的影响，可以看出，基础Stackelberg博弈数据定价模型下，数据平台拥有过高的利润率水平，在数据消费者提升数据价值挖掘能力的过程中，数据生产者和平台的利润率没有明显的提升，而数据平台的利润率提升迅速。基于改进型Stackelberg博弈的数据定价模型中，三者的利润率水平更为均衡，随着数据消费者数据价值挖掘能力的提升，数据生产者、数据消费者的利润率均有所提升，从而鼓励数据消费者提升其数据价值挖掘能力。

图5 数据价值挖掘能力对交易三方利润率的影响Fig. 5 Impact of data value mining ability on data transaction volume and total system utility

2.2.5 数据生产者信息采集效率的影响

分析数据生产者提升信息采集效率1cc的影响，设置1cc=［1/100，1/90，1/80，1/70，1/60，1/50，1/40，1/30，1/20，1/10］ bit·元-1，对应信息采集效率由低到高。将数据消费者的数据需求量级d设置为1，其他参数保持不变。

图6a 显示了信息采集效率对数据交易量的影响，可以看出，基于改进型Stackelberg博弈的数据定价模型下，数据交易信息量随着信息采集效率的提高呈现指数级增长的趋势，而基础模型下增速却十分缓慢，同样论证改进型Stackelberg 博弈的数据定价模型可以激发数据市场活力。图6b 显示了信息采集效率对系统总效用的影响，可以看出，约束数据平台利润率后，整体系统的效用有明显的增加，从而可构建更有利的数据交易市场。

图6 信息采集效率对数据交易量、系统总效用的影响Fig. 6 Impact of information collection efficiency on data transaction volume and total system utility

图7显示了基于改进型Stackelberg 博弈（图7a）和基础Stackelberg博弈（图7b）的两个数据定价模型数据生产者信息采集效率提升对交易三方利润率的影响，可以看出，两个模型都能实现数据生产者在提升其信息采集效率的过程中获利。但是基础Stackelberg 博弈数据定价模型下，数据平台的利润率过高，而数据消费者的利润率过低，并且在数据生产者提升信息采集效率的过程中，数据平台的利润率提升明显，数据消费者的利润率却保持不变。基于改进型Stackelberg 博弈的数据定价模型下，交易三方的利润率更加均衡，且数据消费者同样可以在信息采集效率的提升过程中获取更高的利润率。

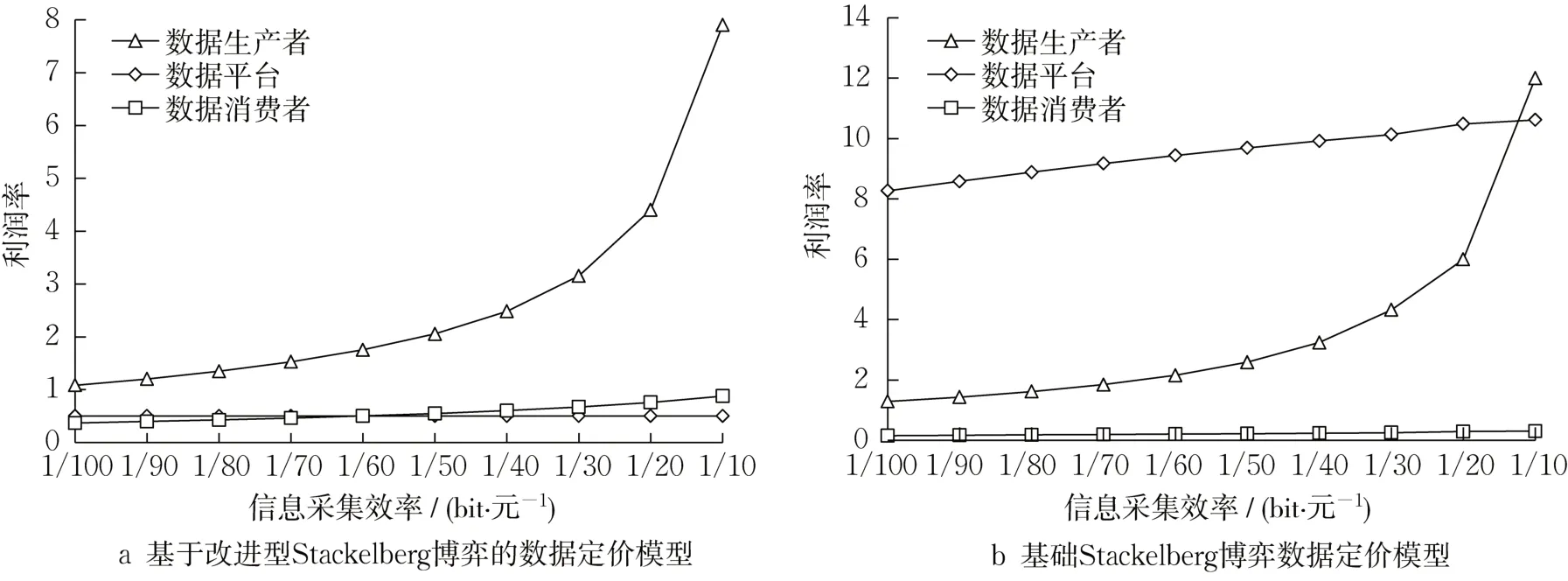
图7 信息采集效率对交易三方利润率的影响Fig. 7 Impact of information collection efficiency on profit rate of three parties in the transaction

3 结论

（1）提出了考虑信息量和平台利润约束的改进型Stackelberg 博弈自动驾驶测试数据定价模型，包含数据信息量评估和数据定价两部分。

（2）在数据信息量评估方面，针对自动驾驶测试数据兼具离散与连续变量，且包含时间戳和经纬度等间接信息特征的特点，在传统信息熵方法的基础上进行了特征挖掘筛选、连续变量离散化、驾驶模式加权等适应性调整，提出了基于特征工程的驾驶模式加权信息熵方法，用于评估自动驾驶测试数据的信息量，并在实际测试数据集上进行了验证。结果表明，相比传统信息熵方法，基于特征工程的驾驶模式加权信息熵方法评估结果和常用分类器准确率均值的变化趋势更为接近，可更有效地表征自动驾驶测试数据的信息量。

（3）在数据定价方面，将数据信息量作为数据交易量的度量单位，提出了考虑信息量和平台利润率约束的改进型Stackelberg 博弈数据定价模型，并进行了实际数据驱动的验证分析。结果表明，该模型可以更合理分配3 个参与方的利润率，并明显提升数据交易量以及系统的总效用，让数据生产者、数据平台分别在提升自身有效信息采集效率、数据价值挖掘能力的过程中获取更多的利益，从而增强自动驾驶测试数据数据交易市场的活力，鼓励数据的生产和消费。此外，数据平台的利润率约束可为相关平台治理型政策制定提供抓手。

作者贡献声明：

涂辉招：研究框架，研究方法，论文撰写 。

刘建泉：定价模型构建。

遇泽洋：研究设计，研究方法，数据分析，论文撰写。

李 浩：定价模型构建，数据分析。

郭新宇：数据分析，论文撰写。

张韬略：研究框架。

孙立军：研究设计。