具有随机波动率方差的信用等级迁移模型

梁 进， 陶晓宇

（同济大学 数学科学学院，上海 200092）

公司债券可能由于因其在到期日资不抵债而无法按面值支付暴露的信用风险越来越为投资者所重视，因此信用评级作为能直接反映信用风险的工具也被应用在债券定价当中。现在学术和市场上的公司债券信用风险分析方法主要分为结构化方法（structural approach）和约化方法（reduced form approach）两类。约化法始于Jarrow和Turnbull的研究，这是一种外生的方法［1］，它不直接考虑违约与公司价值之间的关系，而是通过给定违约概率或者强度来确定违约过程。而结构化方法最早开始于Merton，这是一种内生的方法［2］，所以也被称为基于公司价值（asset-base）模型。

通常认为一个公司的信用等级往往与它本身的资产负债结构密切相关，因此在某些情况下使用内生的结构化方法来刻画公司的信用等级迁移会比约化法更加直观。在结构化方法的框架下，许多学者对信用风险分析方法进行了推广。梁进等［3］首次利用结构化的方法对含信用等级迁移的公司债券进行了研究，他们假设公司资产满足几何布朗运动，有关参数都为常数，利用无套利原理和Feynman Kac 公式得到了偏微分方程及其定解条件，并证明了这个问题解的存在唯一性。Hu等［4］研究了具有信用等级迁移风险的债券定价的自由边界问题，模型中认为信用等级边界和公司的资产负债比有关，通过结构化方法对债券定价并且得到了自由边界问题的一些性质。Liang 等［5］首次将渐近行波解与信用评级迁移问题联系起来，采用自由边界建立了债券定价模型，并证明了解的存在唯一性、唯一性和正则性。Liang 等［6］在结构法框架下，建立了含信用等级迁移的公司债券的效用无差异定价模型；Wu等［7］基于宏观机制转换，建立了一个具有信用等级迁移风险的公司债券估值模型。Wu等［8］采用自由边界模型，在结构化框架下考虑了具有信用等级迁移风险的可违约公司债券的估值。梁进等［9］基于Vasicek 利率模型，对担保信用等级变换的利率互换合约进行了定价，并推导出了相应合约价值的解析解。

上述研究中，信用风险分析方法往往将波动率设为常数，但这显然是理想化的，实际市场上波动率呈现“微笑”效应，将波动率简单地设为常数往往会低估风险，比如经典的Black-Scholes（BS）［10］模型。Scott、Hull 和Wiggins 等对BS 模型进行了推广，以允许随机波动率。Heston［11］在1993 年基于BS 模型和CIR（cox-ingersoll-ross）模型提出了一种随机波动率模型，模型假设公司资产服从几何布朗运动，资产波动率满足CIR［12］模型，实证表明，其隐含波动率与实际更接近，从而得到较广泛的接受。

梁进等［13］基于Heston 模型，针对波动率在高、低等级下定义了不同的长期均值，通过建立随机波动率模型来评估信用等级迁移风险，然后利用一张特殊的零息票来对冲由波动率的随机性造成的风险，最后将问题转化为一个债券价值关于时间、公司资产和波动率的二阶抛物型方程，并推导出在信用等级迁移处的债券价值关于公司资产的一阶导数连续的边值条件，最后采取ADI（alternating direction implicit method）交替方向隐式法求取出数值解。

本文在文献［13］的基础上，同样通过债券定价方式，使用Heston 模型，即资产满足几何布朗运动，资产波动率方差满足CIR过程。基于预先设定的公司资产阈值将公司分为高、低两个等级，与文献［13］不同的是，本文模型考虑到在不同的信用等级下，资产的波动率方差也会有不同的波动性，因此在本文模型中，波动率方差的波动率σ在不同的信用等级下设定为不同的常数，即低等级下σ=σ1，高等级下σ=σ2，且由于低等级下波动更剧烈，因此σ1＞σ2，以此反映资产波动率方差在不同信用等级下的波动情况。于是在不同的信用等级下，公司资产和波动率满足不同的随机过程，以此建立了具有随机波动率方差的信用等级迁移模型。

1 建立具有随机波动率的信用等级迁移模型

1.1 模型假设

假设（1） 市场是完备的，不存在套利机会，无风险利率r。

假设（2） 作为研究工具的公司债券为一张面值为F，到期日为T的零息债券，且违约只发生在到期日T，即到期日的公司资产ST小于F判定为违约，若公司未违约，偿付面值F，反之偿付ST。

假设（3） 记信用等级边界为K，若在t(t≤T)时刻，公司资产St＜K，则认为公司处于低等级，反之处于高等级，公司的信用等级随着St的变化而变化，且假设高、低等级下的债券价值在信用等级边界K处连续。为了满足高等级下债券一定不违约的假设，设定K≥F。

假设（4） 公司资产St和波动率方差vt满足Heston模型，即

式中：、为两个不同的由完备带流概率空间生成的标准布朗运动，且他们的相关系数为ρ；IA是事件A的示性函数；k为均值回归系数；θ为长期均值。

记U=U(St，vt，t)、V=V(St，vt，t)，分别代表低、高等级下的债券价值。低等级下资产波动率方差的波动率为σ1，高等级下资产波动率方差的波动率为σ2，由于低等级下的波动往往要比高等级下的波动剧烈，设定σ2＜σ1。波动率是非负的，根据Feller条件，参数需满足2kθ≥σ2i［12］(i=1，2)。

假设（5） 在到期日，由于低等级债券可能违约，高等级债券一定不会违约，因此，低等级下的债券价值U(ST，vT，T)=min{ST，F}，高等级下的债券价值V(ST，vT，T)=F。

假设（6） 以上假设中的F、K、σi、ρ、r、T、k、θ均为正常数。

1.2 偏微分方程以及边值条件

债券价值U和V是关于随机变量St和vt的函数，因此U和V都实际蕴含两个不同的随机波动项。由假设（1）根据无风险套利，本文运用两种风险资产来对债券的风险进行对冲，其中一种为公司本身的权益资产St，下面借鉴文献［13］引入另外一种特殊的资产P并构建无风险的投资组合，推导得到U和V满足的偏微分方程以及他们满足的边值条件。

1.2.1 引入对冲工具

本文选取一张特殊的利率与资产波动率方差vt变化相一致的零息票作为对冲工具［13］。记零息票为不同信用等级下的零息票价值，P1代表低等级，低等级下t时刻的利率为，利率的波动率为σ1；P2代表高等级，高等级下t时刻的利率为，利率的波动率为σ2，T'为到期日，面值为1。为了保证在每个时刻都能够充分对冲掉公司债券的风险，本文假设T'＞T。由于零息票的利率与资产波动率方差变化相一致，于是

这里的k、θ、、σi同假设（4），于是Pi=Pi(vt，t；σi，T')，再由于Pi是一张零息票，因此它在t时刻的价值等于到期日面值按利率的折现，即

由方程（2）和（3）以及Feynman-Kac 公式［14］，可以推导出在鞅测度下，Pi满足的Cauchy 问题，并得到Pi的解析式为

式中：Ai(t；σi)，Bi(t；σi)满足

1.2.2 偏微分方程的推导

利用1.2.1中引入的特殊的对冲工具Pi以及公司本身的权益资产St来对冲掉债券的风险，通过做多一份公司债券的同时做空份的St以及份的Pi来构造高、低等级下的无风险投资组合。根据Pi的解析式、无风险套利原理和多元Ito公式可以得到份额的表达式以及U和V满足的偏微分方程，份额表达式如下：

结合假设（3）和假设（5）以及偏微分方程，U(S，v，t)和V(S，v，t)是以下边界耦合线性偏微分方程组的解：

事实上，在利用Δ-对冲推导偏微分方程的时候，对迁移边界可以做相似的处理，可以推导出在迁移边界处的边值条件，这个条件方程是一个关于高、低等级债券价值对波动率的一阶偏导和时间的函数，结合这个特殊的方程和公式（6）才构成了本文完整的具有随机波动率方差的信用等级迁移模型。

1.2.3 信用等级迁移边界上条件的推导

本文与文献［13］同样是基于Heston 模型，但后者的信用等级迁移体现在长期均值上，本文的信用等级迁移则是体现在波动率方差的波动率上，因此过信用等级迁移边界的条件不同。根据市场无套利，高、低等级下的无风险投资组合价值在S=K处连续，即

由于高、低等级债券价值在迁移边界处连续U|S=K=V|S=K，根据前面推导出的的表达式，代入式（7）可以得到

由Pi的表达式（4），可以得到Pi关于v的导数为

结合Bi(t；σi)的表达式，得到

将式（10）代入式（8），得到迁移边界处的边值条件为

结合式（11）和方程组（6），就构成了完整的二阶抛物型偏微分方程的定解问题，于是得到了具有随机波动率方差的信用等级迁移模型，即

其中

2 数值结果及参数分析

2.1 蜕化边界的处理

Fichera条件［15］是对具有非负特征的方程在边界上是否应该配置边界条件给定的判定法则。可以看出，v=0 为定解问题（12）的蜕化边界，根据Fichera函数的定义，在边界v=0上，方程的Fichera函数为

由 前 面 的λi(v，t) 表 达 式 ，λi(0，t)=可以证明λi(0，t)是关于t的单调递减的函数，于是B(t，S，0)在t=T处取最小值。当

B(t，S，0)是恒非负的，于是在条件（14）下，不需要在v=0上额外添加边界条件。

2.2 隐差分格式的推导

对于一般的抛物型偏微分方程数值解法如显示格式和隐式格式，前者计算较为简单，却无法保证解是稳定的，而后者可以保证微分方程的解绝对稳定，且不依赖于步长的选取，还有诸如交替方向隐格式（ADI法）、Crank-Nicolson格式［16］等推广方法也是无条件稳定的。本文采取隐差分格式来对问题求取数值解。

2.2.1 偏微分方程的差分化

原问题（12）的变量取值区间为Ω={0 ＜S＜∞，0 ＜v＜∞，0 ＜t＜T}，为了方便求解，取截断边界S∞=v∞=4K，对网格进行剖分，并记

定义如下差分算子：

对式（12）的PDE（partial differential equation）方程进行隐格式差分，得到如下差分方程：

2.2.2 边值条件和终值条件的差分化

（1）v=0、v∞=4K

接下来对边界进行差分化处理。由于v=0 是蜕化边界，且在条件（14）下，不需要在v=0 上额外添加边界条件，于是本文对原始PDE 方程取v=0，可以得到如下的蜕化后的一阶偏微分方程：

同样地，根据上面定义的差分算子式（15）对式（17）进行差分得到v=0上债券价值的差分表达式为

在截断边界v∞=4K处，可以认为波动率趋于无穷时，波动率的微小变化对债券价值的影响不大，因此取

（2）t=T

在终值时刻t=T，根据条件可以得到

（3）S=0、S∞=4K以及迁移边界S=K

在S趋于0 时，可以认为公司处于破产清算阶段，于是取=0，在S∞=4K时，公司不会有违约风险，因此

在信用等级迁移边界S=K处，即i=M时，根据式（11）可以得到

此处的Bi(t)的定义见式（4），对上式进行移项处理得到

根据前面差分后的偏微分方程、终值和边值条件以及各参数间满足的关系，对参数取值。首先设定公司债券的到期日T=1 年，T'＞T，因此假设对冲工具零息票的到期日T'=1.07；公司债券面值F=1 元，K＞F，于是假设信用等级迁移边界K=1.2；固定波动率方差的波动率σ1=0.6，σ2=0.000 7［17］，根据交易所的数据显示，历史年化隐含波动率在股灾期间可超过100%，在这里设定波动率方差的长期均值θ=0.5，根据2kθ≥σ2，于是假设均值回归系数k=0.9；根据市场情况，在大多数时候，1年期国库券的实际利率在3%上下浮动，因此假设无风险利率r=0.03；两个随机过程的相关系数ρ=0.2；经过验算，以上参数取值满足Fichera条件。得到的数值结果如图1～6所示。

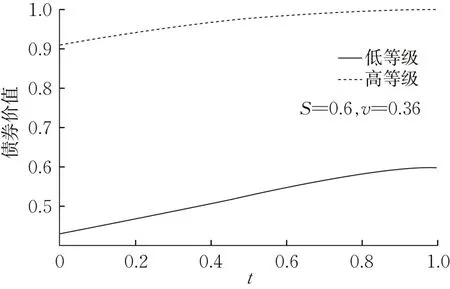
图2 债券价值随时间t的变化Fig. 2 Change in the value of bond with time t

图3 债券价值随资产S的变化Fig. 3 Change in the value of bond with S

从图1可以看出，债券价值关于资产S是单调递增的，并且在低等级下债券价值随着S的增大而快速增大，在高等级下，随着S的增大而增长缓慢。

从图1～6 可以看出，债券价值是随着时间的增大而增大的，并且含信用等级迁移的债券的价值是介于一直处于同一等级的高、低等级债券价值之间。从图4 可以看出，在信用等级迁移边界S=K处，债券价值关于S的一阶导数有一个下凹的尖角，符合模型在边界处带跳的情况，但是由于参数的取值需满足式（19），因此在S=K处的跳数值较小，下凹现象不是特别明显。

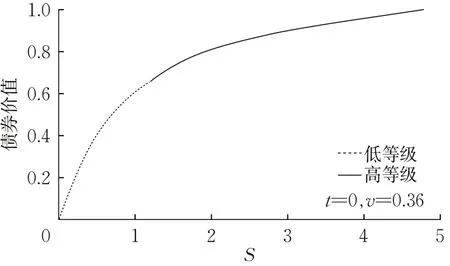
图4 含信用等级迁移债券随资产S的变化Fig. 4 Change of credit rating migration bond with S

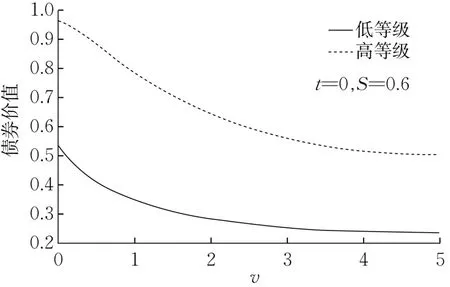
图5 债券价值随波动率v的变化Fig. 5 Change in the value of bond with v

图6 是初始时刻不同波动率方差v下债券价值随资产S的变化曲线，可以看出，在同样的资产S下，债券价值随着波动率的增大而减小。

图6 不同波动率下含信用等级迁移债券随资产S的变化Fig. 6 Change of bond with credit rating migration as asset S changes at different volatilities

2.3 参数分析

通过对各参数进行调整，分析不同参数取值对于债券价值的影响。

图7 是在t=0，v=0.36 时的不同均值回归速度k下债券价值随资产S的变化曲线，可以看出，波动率方差的均值回归速度越大，债券价值越小。实际上，在现实生活中，对于利率来说，回归速度越快，波动越小，即债券凸度带来的收益越小，于是债券价值越低。

图7 不同均值回归速度下含信用等级迁移债券随资产S的变化Fig. 7 Change of migration bonds with credit rating as asset S changes at different mean regression speeds

图8 是t=0，v=0.36 时公司资产和波动率方差满足的两个随机过程的不同相关系数ρ下的债券价值随资产S变化的曲线，可以看出，相关系数ρ越大，债券价值越低，在Shimko等［18］的文章中，也有类似结论。

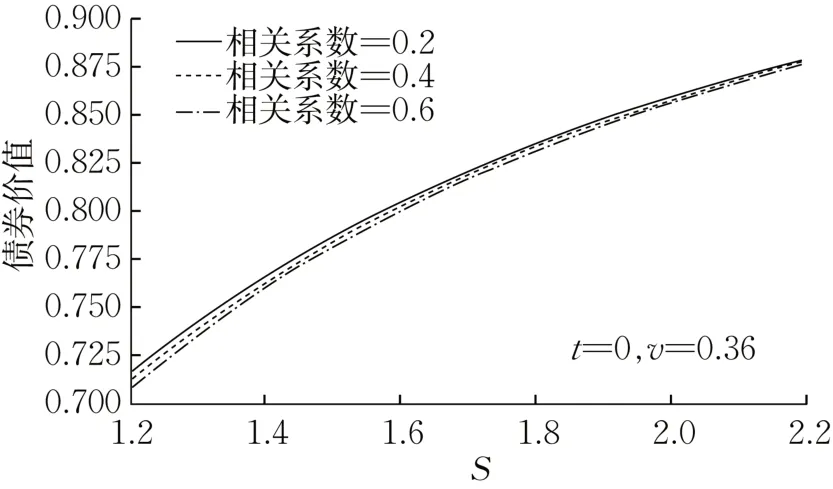
图8 不同相关系数下含信用等级迁移债券随资产S的变化Fig. 8 Change of bonds with credit rating migration as asset S changes at different correlation coefficients

图9是t=0，v=0.36时不同长期均值θ下债券价值随资产S的变化曲线，可以看出，在同一资产S的情况下，均值越大，债券价值越小，实际生活中，θ代表波动率在未来达到稳定后的水平，θ越大代表波动越大，信用风险越大，于是信用利差也会变大，因此债券价值越低。

图9 不同长期均值下含信用等级迁移债券随资产S的变化Fig. 9 Change of bonds with credit rating migration as asset S changes at different long-term means

3 结语

本文以公司债券定价为工具来评估信用等级迁移风险。公司的信用等级由公司资产决定，预先设定信用等级迁移边界将公司分为高等级和低等级，通过将公司资产波动率方差的波动率在不同信用等级下设定为不同的常数，基于Heston 模型，通过债券定价方式，建立了具有随机波动率方差的信用等级迁移模型。然后基于市场无套利的假设，通过对冲的方法将随机微分方程组转化为一个二阶的带内边界的抛物型初边值问题。这个推导出来的定解问题在信用等级迁移边界处的条件不同于一般的边界条件，迁移边界处的跳是一个关于高、低等级债券价值对波动率的一阶偏导和时间的函数，这也是本模型的一个创新之处。后续本文采取了隐格式求取了这个PDE的数值解，并进行了参数分析。

本文将Heston 随机波动率模型应用到公司债券的信用等级迁移风险的研究当中，改进了以Black Sholes模型为基础的信用等级迁移模型中资产波动率为常数的问题。本文模型基于Heston 随机波动率模型，引入不同的“波动率的波动率”来刻画不同信用等级下资产波动率的波动性，同时考虑了波动率与资产价格之间的相关性，以此建立了信用等级迁移模型，也使得信用等级迁移模型更加符合实际。关于本文模型的数值结果，总结得到如下结论：公司处于高等级、公司资产越大、离到期日越近、资产波动率越小、均值回归速度越小、相关系数越小、长期均值越小，都会使得债券价值越大，基本符合实际，因此在实际应用中，要重点关注这几项参数，只有正确估值，才能充分避险。进一步的实际应用价值会在以后的工作中进行实证研究。

作者贡献声明：

梁 进：提出研究选题与模型，研究思路、写作指导。

陶晓宇：负责模型推导，数值计算，论文撰写等。