基于时间重排多重同步压缩S 变换的轴承故障诊断

刘 伟 刘 洋 李双喜 翟志兴 魏文豪

(北京化工大学机电工程学院, 北京 100029)

引 言

滚动轴承在风力涡轮机、航空发动机等高速旋转机械中发挥着重要作用。 轴承故障作为旋转机械最常见的故障之一,一直是故障诊断领域的研究热点[1-4]。 在机械设备的故障诊断中,往往先从传感器采集到的时域信号中获取设备在各个时刻的运行状态,然后对时域信号进行傅里叶变换(Fourier transform,FT)并描述信号的频率分布情况,通过将频率信息与故障频率进行对比来诊断故障。 然而在实际应用中,仅仅依靠时域或频域信息判断设备的健康状况存在一定困难,在此背景下,时频分析(time-frequency analysis,TFA)方法应运而生。

时频分析是一种将一维时域信号映射到二维时频空间的表征方法,它能够反映频率随时间的变化关系和各个时频点的能量强度[5]。 常用的线性时频分析方法包括短时傅里叶变换(short-time Fourier transform,STFT)、连续小波变换(continuous wavelet transform,CWT)和S 变换等。 Auger 等[6]使用重排方法(reassigned method,RM)对时频表示(time-frequency representation, TFR)进行后处理,该方法通过将时频空间中的分散能量聚集到其附近的重心来减少混叠现象,然而同时在时间轴和频率轴压缩能量会导致相位信息丢失,这使得该算法存在不可逆性的缺陷。 为了解决这一难题,Daubechies 等[7]提出了同步压缩变换(synchrosqueezing transform,SST),其核心思想是沿频率方向对TFR 进行能量重排,虽然可读性不如RM 方法,但是该方法具备信号重构能力,且SST 及其高阶版本已经在STFT、CWT和S 变换的应用中取得显著成效[8-10]。 尽管SST在一定程度上提升了线性TFA 方法的能量集中度,但由于线性TFA 方法本身是通过信号和基函数间的内积来定位局部的时变特征,导致该类方法在处理强时变信号时效果不佳。 为此,Yu 等[11-12]提出了多重同步压缩变换(multi-synchrosqueezing transform,MSST),这是一种对TFR 进行多次SST 操作以提升时频分辨率的迭代算法,缺点是会牺牲少量计算成本。 上述方法通常适用于转子碰摩和齿轮故障的诊断。 然而,针对轴承缺陷产生的脉冲信号,需要使用时间分辨率较高的时频分析方法来处理,上述方法对脉冲信号的特征提取效果不佳。 最近,He等[13]提出时间重排同步压缩变换(time-reassigned synchrosqueezing transform,TSST),该方法将TFR 中分散的时频系数重新分配到群延时算子(group delay operator,GDO),从而大大提高了时间方向的分辨率,这对于脉冲特征提取非常重要。

受S 变换、MSST 和TSST 的启发,本文提出一种新的时频分析方法—时间重排多重同步压缩S 变换( time-reassigned multisynchrosqueezing S-transform,TMSSST),该方法对GDO 进行多次迭代,使得时频系数重排目标越来越集中,并接近真实脉冲轨迹。 相较于传统方法,该方法适用于具有快速变化特征的脉冲信号。 同时,通过对TFR 进行时频掩码(time-frequency masking,TFM)可实现对信号的降噪处理。 对于轴承故障,该方法能够获得时间分辨率较高的时频分布,在此基础上可更准确地获取脉冲间隔从而提取故障频率。 最后通过轴承故障的模拟信号和实验信号验证了所提方法的有效性。

1 TMSSST 方法

1.1 S 变换

对于能量有限的信号f,其频域S 变换可以定义为

式中,A(ω)和ϕ(ω)分别表示振幅和相位,-ϕ′(ω)是理想的GDO。 式中的高斯函数为g(t) =()-1e-t2/2σ2, 其傅里叶变换为(ω) =e-ω2σ2/2,这里σ是调整窗宽的重要参数,本文定义σ=()-1,这可以在一定程度上缓解测不准定律。 其中(·^) 表示傅里叶变换,(·)*表示复共轭。

1.2 时间重排同步压缩S 变换

时间重排同步压缩S 变换(TSSST)的核心思想是在S 变换的时间方向进行能量重排,即(t,ω)→((t,ω),ω)。 该方法建立在弱变频信号的假设上,即对于任意频率ω,都存在ε使得max{A′(ω),ϕ″(ω)}≤ε,故(η)可以定义为

将式(3)代入式(2)得到

对式(4)求导可得GDO

联立式(4)和式(5),沿时间方向积分可将模糊的时频能量聚集到GDO 上。

1.3 时间重排多重同步压缩S 变换

TMSSST 具备处理强变频信号的能力,对该类信号而言,对于任意频率ω,都存在ε使得max{A′(ω),ϕ‴(ω)}≤ε,则根据泰勒公式,该信号可以展开为

将式(7)代入式(4)得到

联立式(5)和(8)得到

对SST 变换后的TFR 再次进行压缩,得到新的GDO 为

对比式(9)和式(10)所得GDO 与真实GDO(式(5))间的差值,可知再次压缩后的GDO 更加接近理想值。 文献[12]中定义N次压缩后的GDO 为^t[N](t,ω),故TMSSST 方法中的GDO 可以定义为

可见,当N趋近无穷大时,^t[N](t,ω)就是理想的GDO。 因此,TMSSST 的表达式为

1.4 TMSSST 的信号重构和降噪

沿时间方向对T[N](u,ω)积分,即可获得信号的重构表达式

从复杂信号中提取有效的脉冲特征可以实现轴承故障诊断。 脉冲信号通常具有宽频特征,故常通过最显著时频振幅的频率点来描述脉冲之间的间隔[12]。 由TMSSST 获得的TFR 中每个频率点的包络频率的最大值可以表示为

式中,α(ω)为T[N](:,ω)的平均值。

为了分离信号中的脉冲分量和其他分量,需要在重构过程中利用MF1(u,ω)和MF2(u,ω)对T[N](u,ω)进行时频掩码操作,从而得到高信噪比的时域信号。

式中,β和γ分别表示MF(ω)和∫MF1(u,ω)·|T[N](u,ω)|dω的平均值。 滤波后的重构信号表达式如下。

基于上述TMSSST 的理论推导,给出该算法的实现步骤如下。

1)初始化 输入信号s,迭代数N。

2)计算STGg[h,m],Gdg[h,m]。

3)计算初始GDO

2 TMSSST 在轴承故障诊断中的应用

为了说明所提方法在工程应用中的潜力,本节采用一组轴承内圈故障模拟信号和凯斯西储大学的轴承内外圈故障实验信号对TMSSST 进行验证,并将所得结果与传统时频分析方法作对比。 此外,采用Renyi 熵对时频分布的能量聚焦性进行定量表征。 Renyi 熵是一种常用于度量时频分布能量分散度的指标[14],其值越小表示时频分布的能量越聚焦,在本文中其计算公式为

2.1 模拟信号验证

滚动轴承的局部故障会在轴承和传感器之间产生高频振动[15]。 为了验证TMSSST 方法处理故障冲击引起的轴承共振信号的效果,模拟一组变转速的轴承外圈故障信号s(t)[16]

式中,t和θ分别为离散时间变量和角变量,P为周期调制函数,Q为非负调幅周期函数,N为高斯分布函数,h为脉冲响应函数。 本文所用仿真信号采样频率为10 kHz,轴承的滚动体直径d、节圆直径D、滚动体数z、轴承接触角A、转频f以及对应的故障频率fo如表1 所示。

表1 工况、结构参数和故障频率Table 1 Operating conditions, structural parameters and fault frequency

轴承内圈和外圈故障频率计算公式分别为

该模拟信号的时域波形图如图1(a)所示,可见该信号的冲击明显且规律,其间隔与故障频率大致吻合,且随着转速的线性变化而变化。 但在实际工况中,采集到的信号往往混叠着大量噪声。 为此,将高斯噪声加至模拟信号中得到信噪比(signal-tonoise ratio,SNR)为0 dB 的含噪声信号(图1(b)),其对应的频谱图如图1(c)所示。 由图可看出在噪声影响下难以提取故障特征,观察频谱信息仅能发现其主要频率分布在2 ～4 kHz。

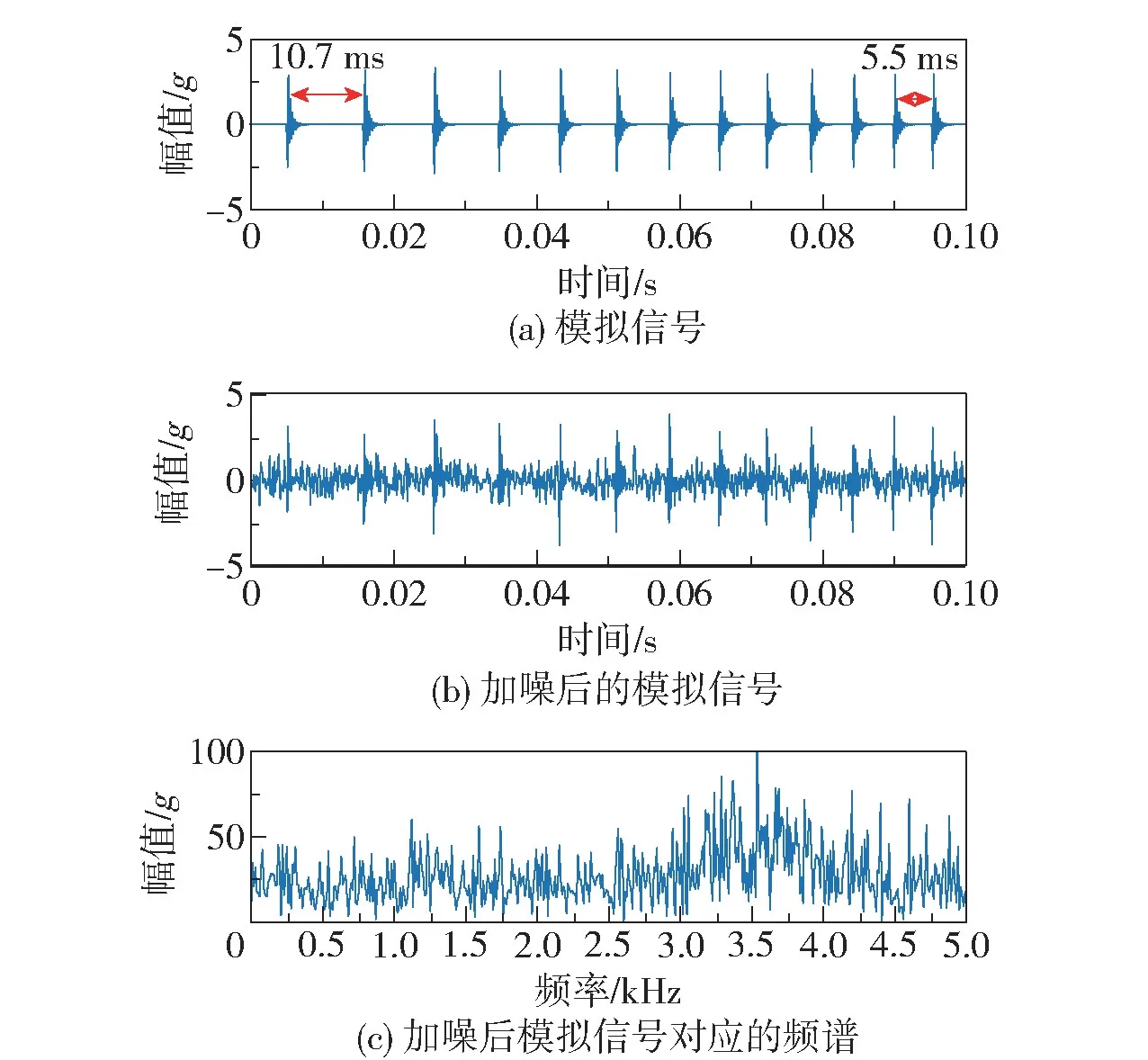
图1 模拟信号、含噪信号及其频谱Fig.1 Simulated signal, noisy signal and its amplitude spectrum

为了提取潜在的故障特征,图2 显示了ST、同步压缩S 变换(synchrosqueezing S-transform,SSST)、二阶同步压缩S 变换(2-order synchrosqueezing Stransform,SSST2)、TSSST 和TMSSST 的TFR。 从图中可以看出,ST 能够检测出每个瞬态冲击的能量和频带,但受限于测不准定律,其TFR 能量发散严重。SSST 和SSST2 虽然大大提高了TFR 的时频分辨率,然而沿频率方向的能量压缩使得该类方法难以检测出冲击故障。 TSSST 在时间方向重新分配能量,从而大大提升了脉冲特征的可读性,不过由于其只使用了一阶GDO 且仅进行单次迭代,产生的模糊结果不适用于故障的精确分析。 TMSSST显示出能量高度集中的TFR,且可以清楚地观察到初始和结束的脉冲间隔分别为10.7 ms 和5.5 ms,对应的故障频率分别为1/10.7 ms =93.5 Hz 和1/5.5 ms =181.8 Hz,与外圈故障频率接近,可以作为故障识别依据。

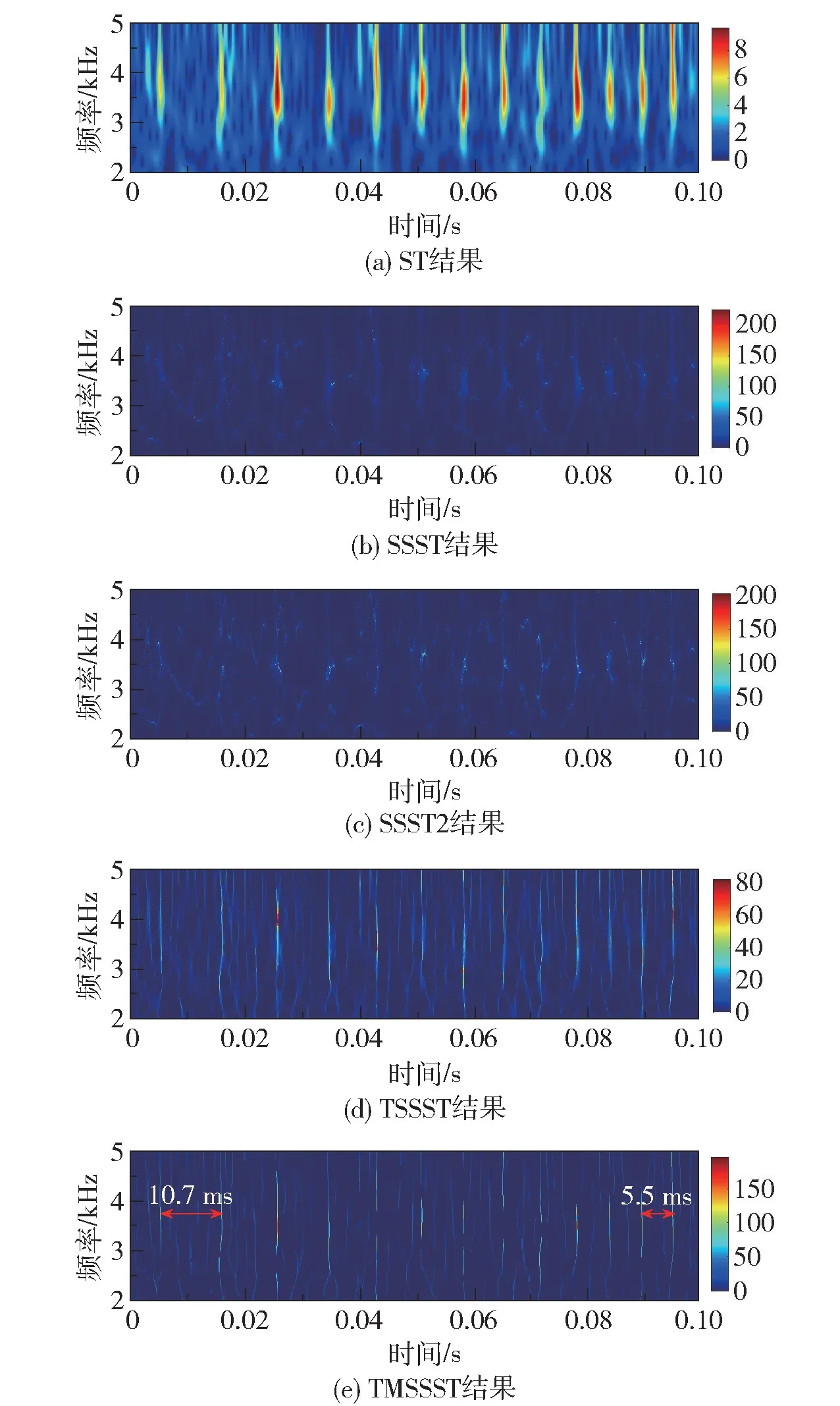
图2 各时频分析方法的时频分布结果Fig.2 TFR results of each time-frequency analysis method

表2 给出了上述方法的Renyi 熵值,可以看出TMSSST 的Renyi 熵值小于其他方法,表明该方法结果的时频能量聚焦性最佳。 为了进一步分析不同方法对于噪声的鲁棒性,对比了上述方法在信噪比为-5 ～15 dB 条件下的Renyi 熵值,如图3 所示。 可以看出对于脉冲信号,频率方向能量压缩对噪声并不敏感,在不同噪声等级下,TMSSST 方法的Renyi熵均为最低。 此外,图4 显示了模拟信号与TMSSST和TSSST 的重构结果对比,可见相比于含噪声信号,TMSSST 滤波后重构的信号与原始信号之间的误差较小,且具有明显的脉冲特征,更适合实际应用中的故障诊断,而TSSST 的重构波形仍包含大量的噪声,与原始信号的误差较大。

图3 模拟信号在信噪比为-5 ～15 dB 下不同方法的Renyi 熵Fig.3 Renyi entropy of the different methods for simulated signals with SNR of -5 to 15 dB

图4 TMSSST 和TSSST 的重构结果与原始信号对比Fig.4 Reconstruction of TMSSST and TSSST results compared with the original signal

表2 不同方法的Renyi 熵Table 2 Renyi entropy of different methods

2.2 实验信号验证

2.2.1 实验信号

以凯斯西储大学数据中心提供的两种类型故障的数据集为实验数据[17],对本文所提方法进行验证。 实验台结构如图5 所示,由电机、扭矩传感器和测力计等组成。 实验通过电火花加工在轴承内圈和外圈两处引发故障,振动信号由置于电机壳体驱动端的加速度传感器记录。 该实验的工况和轴承结构的相关参数如表3 所示,各参数的定义同表1。

图5 轴承实验台Fig.5 Bearing experiment rig

表3 工况、结构参数和故障频率Table 3 Operating conditions, structural parameters and fault frequency

2.2.2 外圈故障信号分析

图6 显示了外圈故障信号的时域波形图及其频谱,可以观察到一些重复性的瞬态冲击,且信号的主要频率分布在1 ～2 kHz。 图7 显示了ST、SSST、SSST2、TSSST 和TMSSST 的TFR 结果。 可以看到,ST 仅仅能够提供模糊的瞬态信息,难以实现精确定位;SSST 和SSST2 的结果在频率方向上的分辨率较好;从TSSST 的结果中能发现较明显的脉冲特征,但其能量有轻微的发散现象;TMSSST 提供了高分辨率的TFR,并能从中定位出脉冲的冲击间隔为9.2 ms 左右,对应的频率为1/9.3 ms=108.7 Hz,基本可以据此判断该轴承存在外圈缺陷。 此外,表4列出了不同时频分析方法对应的Renyi 熵,从表中数值上也能看出TMSSST 是提取脉冲特征的最佳方法。

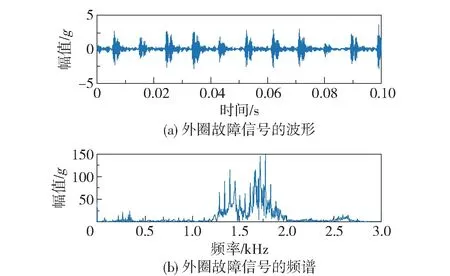
图6 外圈故障信号的波形和频谱Fig.6 Waveform and spectrum of the outer ring fault signal

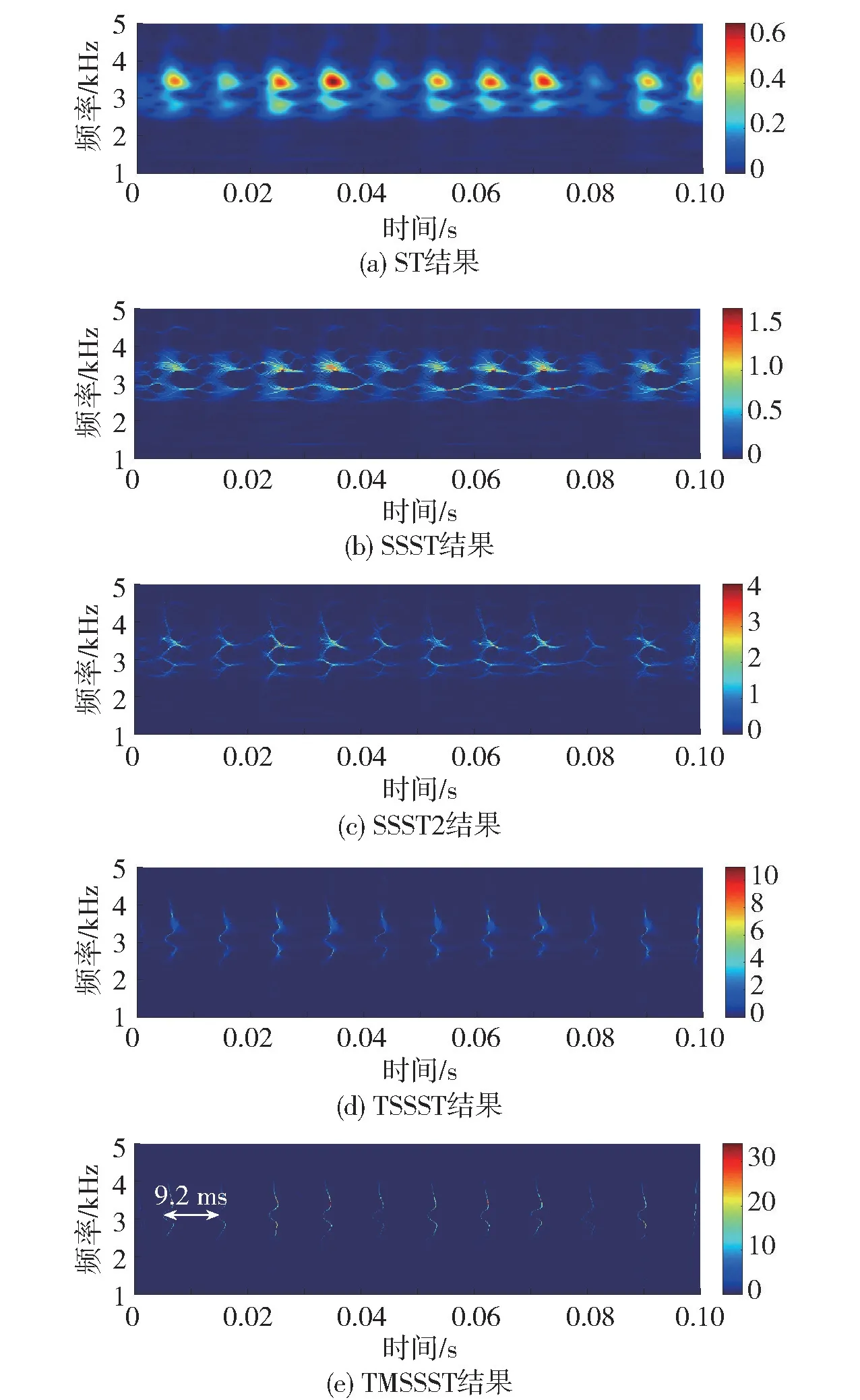
图7 各时频分析方法的时频分布结果Fig.7 TFR results of each time-frequency analysis method

表4 图7 中不同方法的Renyi 熵Table 4 Renyi entropy of the different methods shown in Fig.7

2.2.3 内圈故障信号分析

带有轴承内圈故障的振动信号如图8 所示。 从图中可以看出该信号混叠着大量的噪声,瞬态特征并不显著,能量主要分布在1 ～2 kHz。 图9 给出了轴承内圈故障信号的ST、 SSST、 SSST2、 TSSST和TMSSST 的TFR 结果。 同样地,TMSSST 提供了最具可读性的TFR,且能够准确定位冲击间隔为6.1 ms,根据其对应的频率1/6.1 ms =163.9 Hz 可以判定该轴承存在内圈缺陷。 同样,表5 列出了不同时频分析方法的Renyi 熵,可以看出TMSSST 结果的Renyi 熵低于其他方法,同样说明其TFR 能量集中度最高。

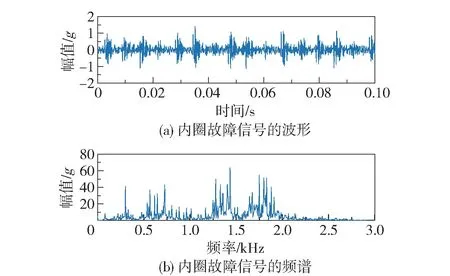
图8 内圈故障信号的波形和频谱Fig.8 Waveform and spectrum of the inner ring fault signal

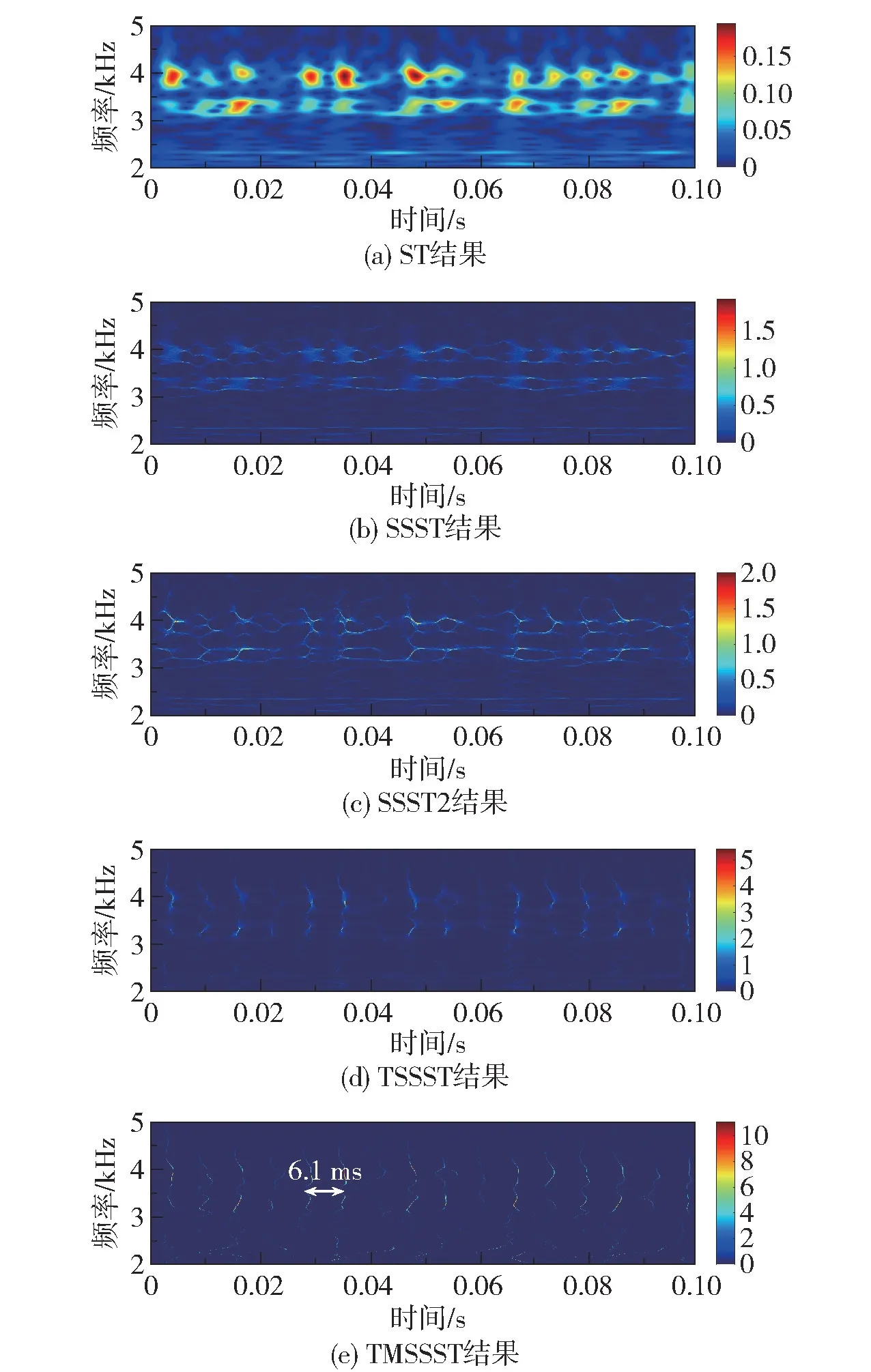
图9 各时频分析方法的时频分布结果Fig.9 TFR results of each time-frequency analysis method

表5 图9 中不同时频分析方法的Renyi 熵Table 5 Renyi entropy of the different methods shown in Fig.9

3 结论

本文提出一种新的时频分析方法—时间重排多重同步压缩S 变换(TMSSST),并将其应用于轴承故障诊断。 该方法通过计算群延时算子来捕获脉冲特征,并采用多次迭代算法解决时频能量发散问题,因此可以更好地处理具有强时变特征的复杂信号。 所提方法的优势在于能够在时间方向产生能量高度集中的时频分布,这对于轴承故障诊断非常关键。 使用噪声污染的模拟信号验证了TMSSST 方法的重构能力和去噪能力;模拟信号和实验信号的对比结果都表明,相比ST、SSST、SSST2 和TSSST 等方法,TMSSST 能够提供时频能量更加集中的时频分布,可以准确地提取脉冲类的故障特征。