无信号环形交叉口机非冲突机器学习预测方法

任丽丽, 吴江玲*, 郭旭亮, 张馨月, 姜涛

(1. 河南大学土木建筑学院, 开封 475004; 2. 长安大学公路学院, 西安 710064)

近年来,交通冲突技术已广泛应用于城市交叉口安全评价,尤其在机非混行严重的无信号环形交叉口安全评价中发挥着极大作用。随着中国机动车、非机动车保有量的急速增长,研究高效精准的交通冲突预测方法,对交管部门主动安全管理和环形交叉口的交通安全评价具有重要意义。

国内外学者在交通冲突预测方面进行了研究。EI-Basyouny等[1]考虑交通量、冲突点所在区域类型(城市/郊区)和几何特征作为变量,利用泊松分布预测交通冲突,研究发现城市比郊区更容易发生冲突。Jia等[2]从无人机视频中提取交通冲突,将其输入基于负二项分布的冲突预测模型中进行实验,结果表明,负二项分布在交通冲突预测中具有一定优势。Cai等[3]通过研究发现泊松分布更适用于双车道匝道的冲突预测,而负二项分布模型适用于单车道匝道的冲突预测。为提高预测精度,研究人员在交通冲突预测中引入机器学习模型。Zhang等[4]和Ihueze[5]利用回归模型拟合交通冲突或碰撞的线性关系,成功预测了交通冲突和交通碰撞。Ge等[6]通过负二项分布预测高速公路养护作业区的交通冲突,研究表明预测模型具有较高精度,能够有效评价交通安全。张婉婷[7]对交叉口进口道的交通冲突进行了研究,采用贝叶斯方法构建负二项分布模型,实验结果表明模型能够有效地实现冲突预测。Zhang等[8]使用多个机器学习模型和Logistic回归预测行人的冲突,并提出了一种基于(extreme gradient boosting, XGBT)模型的行人冲突预测模型,该模型可以预测行人冲突。Guo等[9]使用三个冲突指标,即碰撞时间(time to collision,TTC)、修改碰撞时间[10](modified time to collision,MTTC)和(deceleration rate to avoid collision,DRAC),将机动车冲突以固定的间隔进行汇总,开发了基于实时冲突率的贝叶斯模型。

随着机器学习的发展,有学者将(support vector regression,SVR)模型应用于高速公路交通流预测[11],利用SVR拟合影响因素与交通流之间的非线性关系。已有研究[12-13]也证明了(back propagation, BP)神经网络在拟合非线性数据上的优势。为解决BP神经网络收敛速度慢等问题,邵鑫等[14]通过改进的BP神经网络对交通数据质量进行优化与预测。朱云霞等[15]利用遗传算法(genetic algorithm,GA)优化BP神经网络的权值阈值,结果表明,BP神经网络的预测精度和收敛速度得到很大提升。

城市交叉口具有多车道、车辆运行轨迹随机性高等特点,交通冲突频发。由于交通冲突具有非线性特点,研究人员基于SVR模型和BP神经网络在拟合非线性数据上的优势对交叉口的交通冲突预测进行研究。王鑫[16]研究了交叉口中右转机动车和直行非机动车之间的机非冲突,分别构建基于线性回归和BP神经网络的机非冲突预测模型,结果表明,BP神经网络的预测误差更小。张栋[17]针对环形交叉口的机非冲突预测进行了研究,分别构建了基于负二项分布和BP神经网络的机非冲突预测模型,经对比后发现BP神经网络的预测精度更高。

上述研究主要通过统计模型和单一机器学习模型进行冲突预测,不同的模型均存在一定的适用场景。为了应对复杂的预测问题,文献[18-19]采用组合模型的方式表征交通流数据的所有特征,实现交通流的预测。但是,将组合模型用于交叉口冲突预测的相关研究较少,也未考虑组合模型在交通冲突预测问题上的适用性。因此,为更好地表征机非冲突数据的特征,同时考虑环形交叉口安全评价对机非冲突预测方法的实际需求,现以无人机视频提取的机非冲突数据为基础,引入机器学习算法构建SVR-GA-BP组合模型,对无信号环形交叉口机非冲突进行高效精准的预测。

1 数据采集与提取

1.1 轨迹数据准备

选取开封市天马广场环形交叉口、西安市钟楼环形交叉口、揭阳市东埔环岛、吉林市桦甸市金华路与渤海大街环形交叉口为数据采集地点,进行机非交通冲突调查。利用无人机对各环形交叉口进行高空定点拍摄,采集天气晴天无风,采集时间为工作日的早晚高峰时段,共获得40 h(连续5个工作日)的混合交通流高清视频。利用Tracker软件提取视频中机动车与非机动车的运行轨迹数据,过程如图1所示。

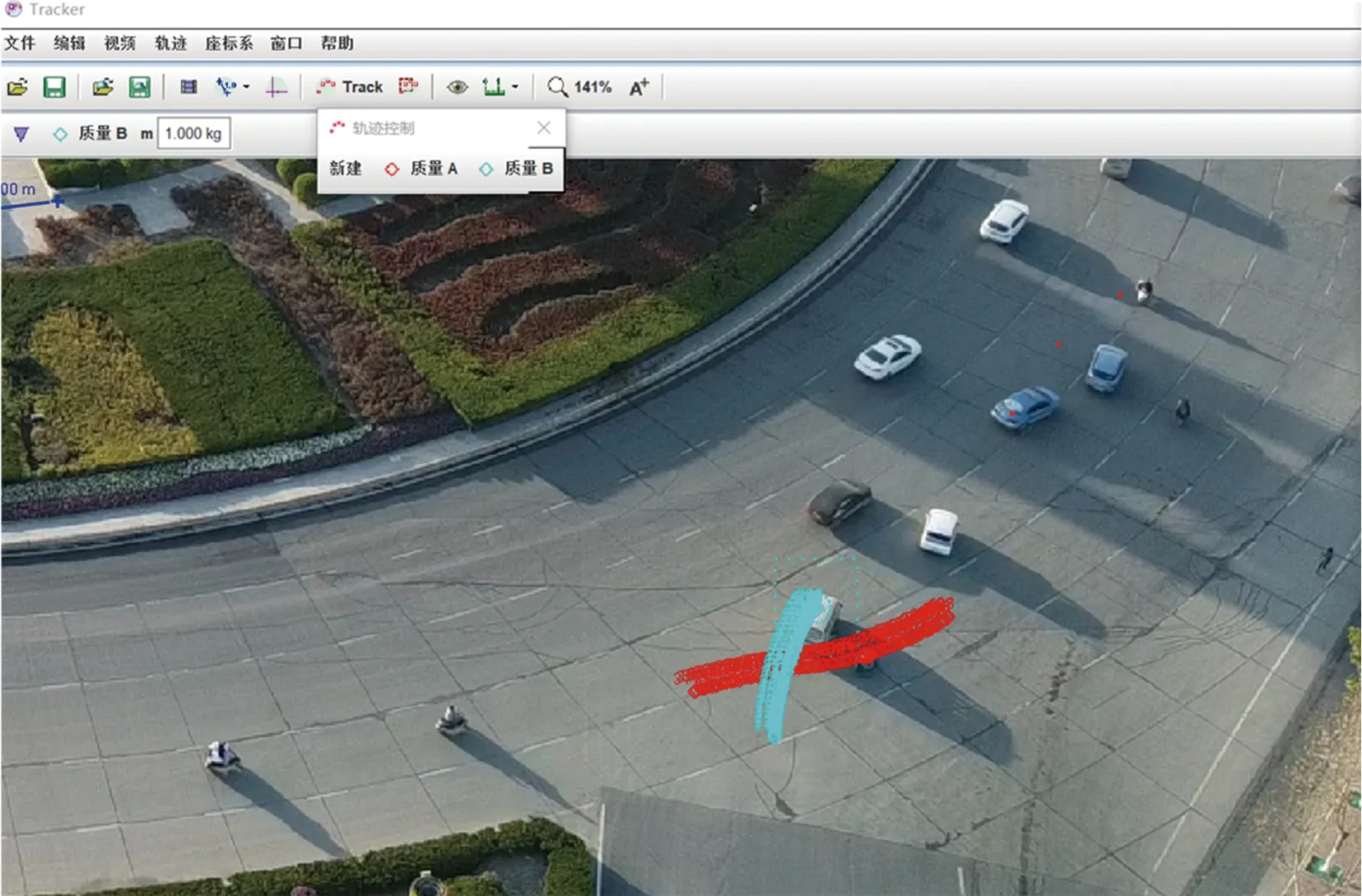
图1 Tracker提取轨迹数据界面Fig.1 Tracker interface for extracting trajectory data

1.2 机非冲突识别

当机动车与非机动车之间存在碰撞可能时,其中至少一方采取制动或转向行为(加速度绝对值大于4 m/s2或行驶方向变化大于30°),可判定为存在避险行为[20]。再以TTC为冲突判别指标进行机非冲突识别,具体流程如图2所示。

根据上述方法得到四个环形交叉口的交通冲突和交通干扰共6 059个。按表1中机非冲突严重程度阈值[17]划分冲突类型,共得到5 143个机非冲突。其中,严重冲突1 189个,占比23.12%,一般冲突3 954个,占比76.88%。选取10 min作为计数单位,非机动车与机动车交通量均采用标准小汽车数,剔除异常数据后共获得一般类型机非交通冲突和严重类型机非交通冲突的样本数据各230组。

图2 机非冲突识别流程Fig.2 Identification process for motorized and non-motorized vehicles conflicts

表1 机非交通冲突严重程度阈值划分Table 1 Thresholds for traffic conflict severity classifications

1.3 影响因素提取与分析

通过分析机非冲突的空间分布,能够为确定机非冲突的影响因素提供科学依据。利用地理信息系统(geographic information system,GIS)技术得到机非冲突分布热力图,如图3所示。根据图3可知,机非冲突的空间分布情况如下。

(1)一般冲突数量较多,冲突点位置较为离散,大部分冲突点位于交织区内,热力图面积大;严重冲突的位置较为集中,数量较少,热力图面积小。

(2)一般机非冲突和严重机非冲突主要集中在交织区的入口处和出口处以及交织区的外侧车道。因为在交织区入口处和出口处容易发生的冲突包括右转机动车与直行非机动车之间的冲突、右转非机动车与直行机动车之间的冲突、右转机动车与右转非机动车之间的冲突;在交织区外侧车道处由于在驶入和驶出环岛时非机动车行驶较为混乱,造成交织区内出现机非冲突。

交通流特性与交叉口的交通冲突存在较强关联[21-22]。初步选择机非冲突的影响因素为交通量、平均速度、大车比例。结合冲突的空间分布情况详细划分影响因素,并利用偏相关分析法对所有影响因素进行分析,确定机非冲突的显著影响因素。

根据表2偏相关分析结果,在一般类型机非交通冲突中,B1、B2、B3、E1、E2、E3等显著性明显大于0.05,因此剔除这些因素;在严重类型机非交通冲突预测中,C1、C2、C3、E1、E2、E3等显著性明显大于0.05,同样将其剔除。最终筛选的显著影响因素如表3所示。

2 SVR-GA-BP机非冲突预测模型

2.1 支持向量回归模型

机非冲突样本数据具有多影响因素、非线性、小样本等特点,而支持向量回归模型(SVR)通过非线性映射方式将样本从低维空间映射到高维特征空间中进行线性回归,能够有效解决非线性、高维数、小样本的预测问题[23]。

SVR对机非冲突样本数据进行非线性映射,其超平面公式为

f(xi)=ωTφ(xi)+b

(1)

式(1)中:ω为权重向量;b为偏置;φ(xi)为xi映射到高维空间的特征向量。

ω和b为SVR通过核函数与损失函数得出超平面f(xi)的最优解,进而将机非冲突预测问题转化为凸二次规划问题。SVR的损失函数和凸二次规划问题的目标函数表达式分别为

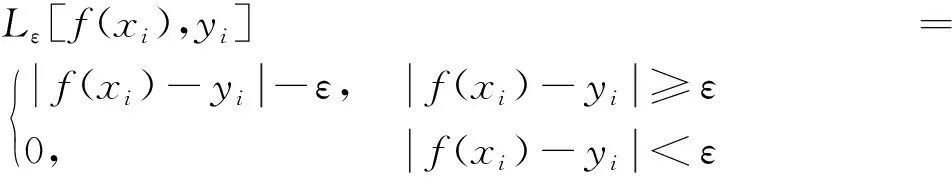
(2)

(3)

(4)

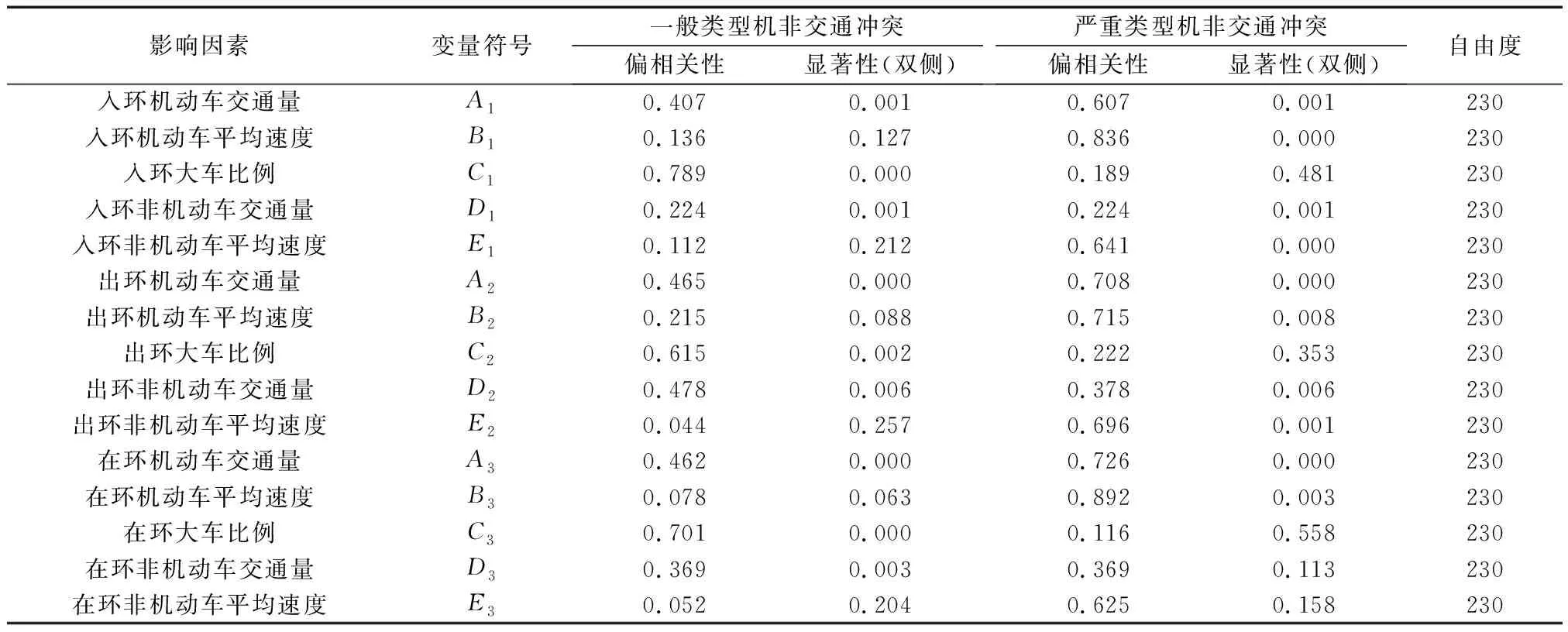
表2 影响因素偏相关分析结果Table 2 Partial correlation analysis results of influencing factors

表3 无信号环形交叉口交通冲突显著影响因素Table 3 Significant influencing factors of traffic conflict at unsignalized roundabouts

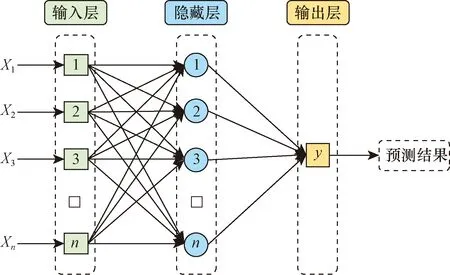
图4 BP神经网络结构Fig.4 The structure of BP neural network

综上,SVR模型最终得到超平面仅与支持向量有关,具有泛化能力强、鲁棒性高、运算速率快等特点。

2.2 BP神经网络

BP神经网络是按照误差逆传播算法训练的多层前馈神经网络,结构上包括输入层、输出层及隐藏层,并采用全连接方式,具体结构如图4所示[17]。

基于机非冲突预测的BP神经网络包括前向信息传递和反向误差传播阶段,步骤如下。

(1)在前向信息传递阶段,输入层接收机非冲突样本影响因素并将信息传递至隐藏层进行处理。

(2)隐藏层根据对应的连接权重对从输入层传递过来的信息加权求和,将其非线性映射生成输出传递至输出层。

(3)若输出层的输出不符合期望输出,则进入反向误差传播阶段,根据误差不断对网络的权值和阈值进行调整。

(4)经过不断迭代,使得输出的冲突预测结果逐渐逼近期望输出。

BP神经网络模型输入为机非冲突样本影响因素,模型输出为机非冲突数量,两者之间关系式为

(5)

式(5)中:n为输入层节点数;q为隐含层节点数;ωij为第i个输入层节点与第j个隐含层节点连接权值;xi为第i个输入层节点的机非冲突样本的影响因素;yt为机非冲突数量的预测值;bj为第j个隐藏层节点阈值;f1为隐藏层节点激励函数;vjt为第j个隐藏层节点和第t个输出层节点连接权值;bt为第t个输出层节点阈值;f0为输出层节点传递函数。

结合冲突样本的数据特点,选用经典三层BP神经网络,通过机非冲突的影响因素预测冲突数量,隐藏层激活函数选用Sigmoid函数。由于样本数据中存在9种影响因素,因变量仅为交通冲突数,因此将输入层节点数设为9,输出层节点数设为1。隐藏层节点数通常根据经验公式和多次实验来确定,经验公式为:

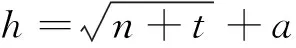
(6)

式(6)中:n为输入层节点个数;t为输出层节点个数;a一般为[1,10]之间的常数。

综上,BP神经网络具有自适应能力和较强的非线性关系映射能力,适用于拟合非线性关系。

2.3 SVR-GA-BP组合模型建立

根据前述内容可知SVR模型具有高效性和BP神经网络预测性能较好。将两者优势相结合构建组合模型能够减少算法耗时和提高预测准确性,有效平衡过拟合和欠拟合问题[24]。同时,考虑BP神经网络陷入局部极小值导致训练失败,引入遗传算法对BP神经网络的初始权重和阈值进行优化,以改进网络性能。最终,构建SVR-GA-BP组合模型对机非冲突进行预测,预测模型思路如下。

(1)利用SVR提取冲突样本中的支持向量。

(2)计算支持向量被选入构建新样本数据集的概率,表达式为

(7)

式(7)中:l(x)为支持向量x与硬ε带之间的距离,p(x)为支持向量x被选入构建新样本数据集的概率。

(3)将新样本数据集作为模型时如输入到BP神经网络中,设定BP神经网络初始权重和阈值。

(4)初始化编码种群。对BP神经网络初始权重和阈值进行二进制编码,确定个体编码长度。

(5)将BP神经网络训练均方根误差RMSE作为适应度值。

(6)经计算后的个体适应度小于已确定的适应度,满足终止迭代条件,转入步骤(7),否则执行选择、交叉、变异运算生成新种群,重新计算个体适应度并判断是否满足终止迭代条件。

(7)将遗传算法的最优个体还原为优化后的初始权重和阈值。

(8)将优化后的初始权重和阈值输入BP神经网络进行训练。

(9)将冲突测试样本数据集输入到训练好的模型中,进行机非冲突预测。

(10)得到预测结果,进行预测性能评价。

基于上述步骤可明确SVR-GA-BP组合模型结构,如图5所示。

3 机非冲突预测实验

3.1 数据准备

基于冲突样本构建样本数据集并将其用于单一预测模型和组合预测模型。按照8∶2的比例将样本数据集随机划分为训练集和测试集,训练集包含184组数据,用于训练预测模型;测试集包含46组数据,用于验证模型的有效性。为提高模型预测精度和可信度,对数据集归一化处理,将其缩小至[0,1]区间上,消除数据的数量级差异对预测结果的影响,最终得到训练集数据样本和测试集数据样本。数据归一化公式为

(8)

式(8)中:x′为归一化处理后的结果;x为机非冲突样本数据;xmax和xmin分别为机非冲突样本数据最大值和最小值。

3.2 模型参数设置

本文提出的SVR-GA-BP组合模型包含基于GA算法优化的BP神经网络和SVR模型,需要设置的参数包含三个方面。

(1)SVR模型参数通过多次实验得到以下设置:核函数为高斯核函数(radial basis function,RBF),核函数参数σ设置为2,损失函数的参数ε设为0.2,惩罚参数C设为1.0。

(2)根据样本数据集的格式,影响因素个数为9,故BP神经网络的输入层节点数量设为9;模型输出结果仅为交通冲突数量,故输出层节点数量设为1。隐藏层节点数量根据经验公式和多次实验对比设为4。为获取较准确冲突预测结果,选择0.01作为学习率值。激活函数为Sigmoid函数。

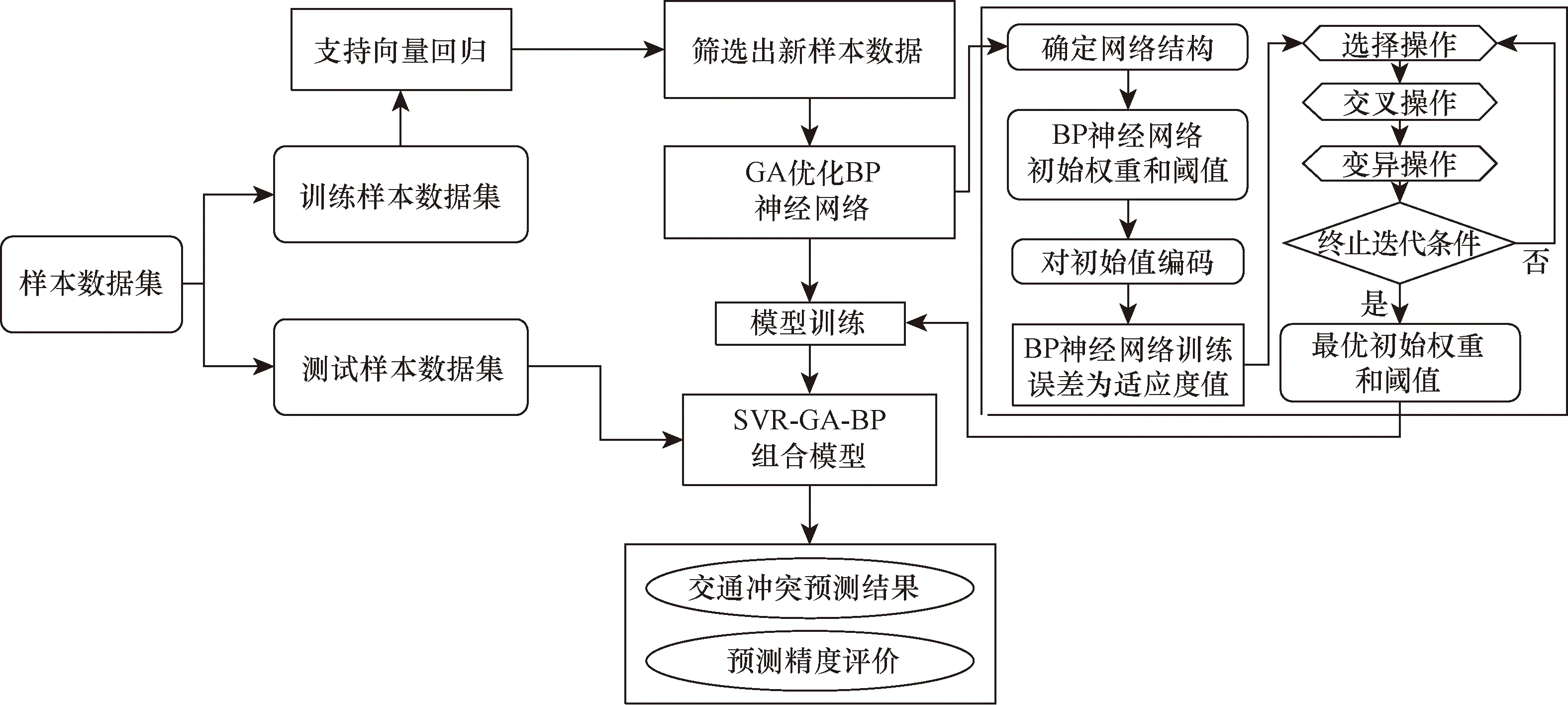
图5 SVR-GA-BP组合模型的结构Fig.5 Structure of the SVR-GA-BP combined model

(3)基于BP神经网络训练得到的均方根误差和参数适应度之间的关系,通过多次实验比较分析发现,遗传算法(GA)的群体大小设置为30,交叉概率设置为0.8,变异概率设置为0.005,迭代次数设置为80时,BP神经网络能够得到最优参数,即最优的初始权重和阈值。

3.3 预测性能评估指标

为评价预测模型的效果,选取均方根误差(root mean squared error,RMSE)、平均绝对误差(mean absolute error,MAE)、(mean absolute percentage error,MAPE)计算模型的预测误差,准确率(accuracy)、决定系数(R2)衡量组合模型的预测精度,各评价指标的具体计算公式如下所示。

(1)均方根误差:

(9)

(2)平均绝对误差:

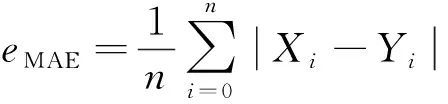
(10)

(3)平均绝对百分比误差:

(11)

(4)准确率:

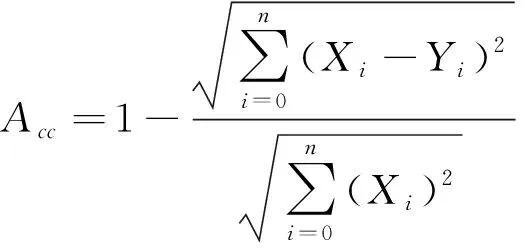
(12)

(5)决定系数:

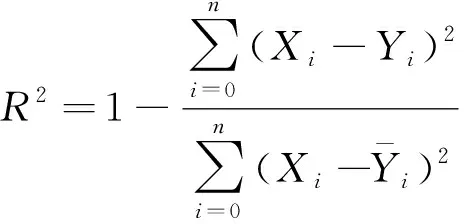
(13)

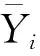
3.4 预测结果对比分析

为验证本文所提组合模型在冲突预测中的有效性,分别利用SVR-GA-BP组合模型、SVR模型、BP神经网络进行预测实验,并对比分析预测结果。通过将相同训练集数据分别导入不同预测模型,得到一般类型机非交通冲突预测结果和严重类型机非交通冲突预测结果如图6(a)和图6(b)所示。实验中两种类型机非冲突预测模型的参数一致。

从图6可以直接看出,三种模型预测结果总体趋势一致。其中,SVR-GA-BP组合模型比单一的BP神经网络和SVR模型在数据预测方面更精准,预测结果更接近真实值。例如,编号为15的一般类型机非冲突样本实测值为17,SVR预测值为18.30,BP预测值为19.21,SVR-GA-BP预测值为17.40,对比后可以发现SVR-GA-BP的预测值与实测值最为接近;编号为15的严重类型机非冲突样本实测值为4,SVR预测值为5.38,BP预测值为4.53,SVR-GA-BP预测值为4.30,对比后同样可以发现SVR-GA-BP的预测值与实测值误差最小。

图6 机非交通冲突预测结果Fig.6 Traffic conflict prediction results of motorized and non-motorized vehicles

三种模型在不同冲突类型下的预测误差曲线如图7所示。由图7(a)可以看出,在一般类型机非冲突预测实验中,SVR模型最大预测误差超过35%;BP神经网络大部分预测误差超过10%;SVR-GA-BP组合模型的误差最小,最大预测误差不超过10%。由图7(b)可以看出,在严重类型机非冲突预测实验中,SVR模型的预测误差最大,大部分预测误差超过15%;BP神经网络大部分预测误差在10%至20%范围内;SVR-GA-BP组合模型最大预测误差仍未超过10%。

为进一步分析不同模型的预测性能,分别计算相应的性能评价指标,如表4和表5所示。由表4和表5可以得出:

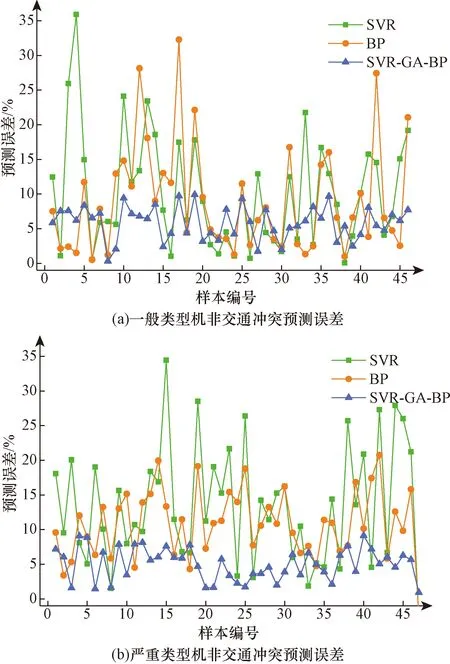
图7 机非交通冲突预测误差Fig.7 Traffic conflict prediction errors of motorized and non-motorized vehicles

(1)在一般类型机非交通冲突预测中,与SVR模型相比,SVR-GA-BP组合预测模型的RMSE、MAE、MAPE分别降低了0.725 1、0.521 3、6.61%,准确率和R2分别提高了0.069和0.025;与BP神经网络相比,SVR-GA-BP组合预测模型的RMSE、MAE、MAPE分别降低了0.82、0.509 8、3.13%,准确率和R2分别提高0.073和0.051。结果说明,在一般类型机非冲突预测中,本文提出的SVR-GA-BP组合模型预测性能更优。

(2)在严重类型机非交通冲突预测中,与SVR模型相比,SVR-GA-BP组合预测模型的RMSE、MAE、MAPE分别降低了0.493 5、0.420 7、8.69%,准确率和R2分别提高了0.109和0.144;与BP神经网络相比,SVR-GA-BP组合预测模型的RMSE、MAE、MAPE分别降低了0.327 1、0.304 3、5.99%,准确率和R2分别提高0.08和0.096。在严重类型机非冲突预测中,本文提出的SVR-GA-BP组合模型预测性能更优。

综上所述,本文提出的SVR-GA-BP组合模型在预测性能上均优于BP神经网络和SVR模型,预测精度更高且数据拟合能力更优。

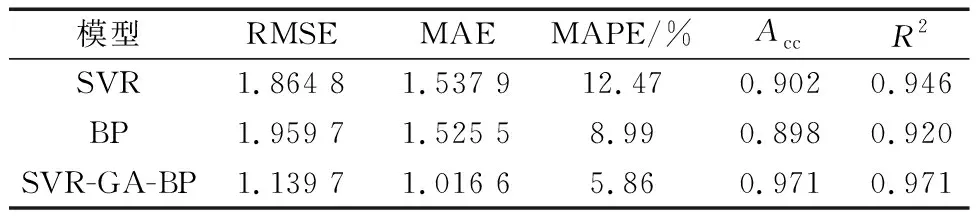
表4 一般类型机非交通冲突预测性能评价表Table 4 Predictive performance for minor traffic conflicts

表5 严重类型机非交通冲突预测性能评价表Table 5 Predictive performance for serious traffic conflicts

4 结论

利用无人机视频获取机非冲突样本,通过分析机非冲突的空间分布,进而确定影响因素,引入机器学习模型构建了一种机非冲突组合预测模型(SVR-GA-BP),得到如下结论。

(1)无信号环形交叉口的机非冲突主要发生在交织区入口处和出口处以及交织区内的外侧车道,其位置与入环、出环、在环行驶的车辆速度、交通量、大车比例有显著关系。

(2)机非冲突预测模型可以利用直接测量的交通量数据、车辆运行速度数据、车辆类型占比得到机非冲突数据,在一定程度上避免了基于视频数据识别交通冲突的复杂工作。相比单一机器学习模型,SVR-GA-BP组合模型能够有效提高机非冲突的预测精度,使预测值更接近真实值。

(3)现实中无信号环形交叉口的机非冲突还可能受到如天气状况、道路状况、节假日、驾驶人性别、交叉口几何特征等多种因素的影响,尚未将上述因素纳入模型的考虑范围;同时,实验数据仅针对无信号的平面环形交叉口,未考虑模型在立体环形交叉口的适用性。在未来研究中需增加环形交叉口的类型和更充分的数据采集及模型验证。