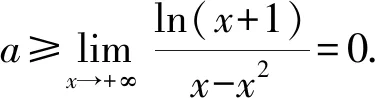从“端点效应”到“内点效应”导数恒成立求参数取值范围问题
2023-12-08李文东
李文东
(中山市中山纪念中学,广东 中山 528454)
导数恒成立求参数取值范围问题一直是高考的热点,同时也是难点问题.解决这一类问题需要用到函数与方程思想、转化与化归思想、数形结合思想和分类讨论等数学思想,能够很好地发展和培养学生的数学抽象、直观想象、逻辑推理和数学运算等核心素养.其中“端点效应”经常被用来求解一类恒成立问题.关于“端点效应”其中一个比较具体的模型是:若∀x∈[a,b],f(x,m)≥0,且f(a)=0,则必然∃x0∈(a,b),当x∈[a,x0]时f(x)单调递增,从而有x∈[a,x0]时,f′(x)≥0成立,特别有f′(a)≥0这一必要条件,由此可得出参数m的范围,然后说明这一范围的充分性即可[1].
1 利用“端点效应”求解参数取值范围问题
例1(2016年全国Ⅱ卷文科第21题改编)已知函数f(x)=(x+1)lnx-a(x-1),当x∈(1,+∞)时,f(x)>0,求a的取值范围.
解析注意到f(1)=0,要使得当x∈(1,+∞)时,f(x)>0,则必有f′(1)≥0.

所以f′(1)=2-a≥0,解得a≤2(必要性).
下面证明a≤2的充分性,即当a≤2时,f(x)>0成立.
由于当a≤2时,

所以函数g(x)在[1,+∞)单调递增.
故g(x)>g(1)=0.从而f′(x)>0.
即函数f(x)在[1,+∞)单调递增.
故f(x)>f(1)=0,符合题意.
综上所述,a的取值范围为(-∞,2].
2 对利用“端点效应”求解参数取值范围问题充分性的思考
虽然例1中利用“端点效应”得出的参数的范围具有充分性,而且这样的例子还不在少数,但是并不能说明用“端点效应”得到的结果就是最终的正确答案.

分析我们尝试用“端点效应”来解决该问题:


注意到g′(0)=0,g″(x)=ex+2a-3x,

但是这个范围却不是正确的答案.
其实本题用分离参数法很容易求解.
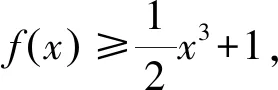
(1)当x=0时,不等式显然成立,符合题意;
(2)当x>0时,分离参数a,得


h′(x)=ex-x-1,h″(x)=ex-1≥0.
故h′(x)单调递增,h′(x)≥h′(0)=0.
故函数h(x)单调递增,h(x)≥h(0)=0.
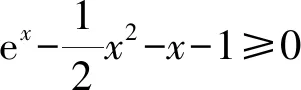
故当x∈(0,2)时,g′(x)>0,g(x)单调递增;
当x∈(2,+∞)时,g′(x)<0,g(x)单调递减.

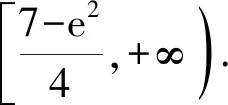



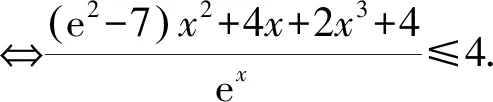



从而[h(x)]max=max{h(0),h(2)}=4,即h(x)≤4,①式成立.


由此可见,本题中的“端点效应”失效了,而应该在内点x=2处求解.那么我们应该怎样才能迅速找到这个“内点”呢[1]?

图的图象

我们用上述方法再次求解问题1.



解得x0=0 或x0=2.

3 运用“端点效应”和“内点效应”求参数取值范围问题举例
对于无法采用分离参数的恒成立问题,上述找“内点”的方法也是可以的.
例3(2020年山东新高考Ⅰ卷理21题第(2)问)已知函数f(x)=aex-1-lnx+lna.若不等式f(x)≥1恒成立,求a的取值范围.
解析设g(x)=f(x)-1=aex-1-lnx+lna-1.


解得x0=1.所以f(1)≥1,即a+lna≥1.

所以S(a)在区间(0,+∞)内单调递增.
因为S(1)=1,所以a≥1时,有S(a)≥S(1),即a+lna≥1.
下面证明当a≥1时,f(x)≥1恒成立.
令T(a)=aex-1-lnx+lna,只需证当a≥1时,T(a)≥1恒成立.

所以T(a)在区间[1,+∞)上单调递增.
则[T(a)]min=T(1)=ex-1-lnx.
因此要证明a≥1时,T(a)≥1恒成立,只需证明[T(a)]min=ex-1-lnx≥1即可.
由ex≥x+1,lnx≤x-1,得ex-1≥x,-lnx≥1-x.
上面两个不等式两边相加可得ex-1-lnx≥1.
故a≥1时,f(x)≥1恒成立.
当0 所以a的取值范围为a≥1. 若无内点,则这个时候我们就可以继续用“端点效应”. 例4(2015年山东高考理22题第(2)问)设函数f(x)=ln(x+1)+a(x2-x),其中a∈R.若∀x>0,f(x)≥0成立,求a的取值范围. 消去a得x0(1-x0)=(1-2x0)(x0+1)ln(x0+1).解得x0=0.注意到f(0)=0,又∀x>0,f(x)≥0成立,从而必有f′(0)≥0,得a≤1. 下面证明当0≤a≤1时,f(x)=ln(x+1)+a(x2-x)≥0恒成立.显然当x≥1时,f(x)>0成立;当0 f(x)=ln(x+1)+a(x2-x)≥ln(x+1)+x2-x. 令g(x)=ln(x+1)+x2-x,x∈(0,1),则 故g(x)>g(0)=0.从而有f(x)>0恒成立. 故a的取值范围为[0,1]. 例5 若不等式sinx-x+ax2≥0恒成立,求a的取值范围. 解析设f(x)=sinx-x+ax2, 解得x0=(2k+1)π,k∈Z. 根据对称性,只需证明: 运用“端点效应”和“内点效应”求解f(x,a)≥0恒成立时参数取值范围问题的一般步骤: (1)解方程组f(x0,a)=0且f′(x0,a)=0,消去参数a可得关于x0的方程; (2)若(1)中的方程的解恰好是区间的端点,则可以利用“端点效应”方法求解,同时注意在无穷端点(若区间是无穷的)处的情况; (3)若(1)中的解不是区间的端点,则这些点为内点,可用“内点效应”求解; (4)若(1)中的方程无解,则说明该问题不适合用“端点效应”和“内点效应”求解.