基于NSGA-Ⅱ算法的分布式冷热电联产系统低碳经济运行策略

陈程，林仕立，张先勇，李晟

(1.广东技术师范大学 自动化学院，广东 广州 510450；2.水发兴业能源(珠海)有限公司，广东 珠海 519085)

提高综合能源系统的能源利用效率，是实现“双碳”目标的重要举措之一[1]。大型建筑、园区等多采用电网供电和集中供热的供能方式，一次能源利用率不到40%，容易造成能源浪费并产生额外的碳排放[2]，因而由可再生能源、中小型燃气机组等作为供能主体的分布式冷热电联产(combined cooling heating and power，CCHP)系统受到了越来越广泛的关注[3-6]。相比传统分供式系统，CCHP系统可以有效利用光伏、风电等可再生能源和燃气机组余热，实现能源的本地生产、就近消费和梯次利用，从而有效减少系统运行过程中的碳排放量并降低成本[7-11]。随着CCHP系统在能源系统中的作用不断增大，目前其已在海岛、偏远地区等孤岛型系统和智能园区、商业建筑群等并网型系统中得到了实际应用[12]。

影响CCHP系统性能的因素众多，所以合理的配置、控制和管理对其至关重要，而控制策略是实现系统低碳经济运行的关键。当前CCHP系统主要采用传统内燃机“以热定电”或者“以电定热”的规则运行控制策略，在多数场景下无法高效发挥能源综合利用的优势。为实现规则控制算法的优化，冯乐军等提出基于用户负荷时间参数的CCHP用户分类方法，根据用户类型对传统规则运行策略进行调节[13]。杜传铭等分别在“以热定电”和“以电定热”2种运行模式下开展实验分析，得出采用混合控制模式的CCHP系统各项指标评价均优于分供系统[14]。Feng等对“以热定电”与“以电定热”2种运行模式下CCHP系统进行评估，得出当建筑物的冷热负荷与电负荷之比远大于CCHP系统原动机的热电比时，“以电定热”运行方式的控制效果更好[15]。刘星月等从能源、环境、经济和综合4个方面评估系统的容量配置、控制策略，得出当系统采用“以热定电”运行方式时，太阳能光伏光热综合利用的控制策略优于“以电定热”[16]。

上述基于规则的优化策略在一定程度上提高了CCHP系统性能，但受限于供需侧不平衡、负荷实时波动等的影响，往往难以使得产能设备运行在理想状态区间，因此，基于智能算法的CCHP系统控制策略逐渐开始被研究。Ghersi等提出一种改进型电力负荷跟踪策略，通过遗传算法对CCHP系统容量进行最优匹配，降低了系统碳排放并具备更好的经济性[17]。Zheng等采用多目标粒子群算法优化CCHP系统控制策略，在降低累计投资成本的同时还可提供更好的供电可靠性和碳排放指标[18]。Ji等通过改进型蚁狮算法优化CCHP系统设备容量和运行策略，提高了一次能源利用率与综合评价指标[19]。Guo等提出基于质子交换膜燃料电池的CCHP系统，并采用蜉蝣算法解决算法过早收敛的问题[20]。另外，非支配排序遗传算法Ⅱ(non-dominated sorting genetic algorithm-Ⅱ，NSGA-Ⅱ)在系统多目标优化中也有着广泛的应用与研究[21-22]。

上述研究表明基于智能算法的分布式能源系统运行控制策略，可以提高系统性能、节能率并降低运行成本，但其应用于实际系统时仍存在调试时间较长、控制器成本过高等问题，且多数仅针对独立系统或并网不上网系统。因此，本文考虑CCHP系统并网且上网模式，研究基于NSGA-Ⅱ算法的运行控制策略，提出结合融合拥挤度算子和初始约束条件的改进型NAGA-Ⅱ算法，以此优化NSGA-Ⅱ种群生成以及约束条件的计算方式，并分析其与传统基于规则的运行调度方法的控制效果，以有效实现电-气综合CCHP系统的低碳经济运行。

1 CCHP系统拓扑结构

考虑到天然气高热值和低污染的优点，当前CCHP系统一般采用燃气机组作为供能主体，提供系统所需的电能和热能；同时，电网和燃气锅炉作为辅助支撑系统，用于满足系统电负荷、热负荷、冷负荷的基本需求。此外，采用可再生能源联合供能是CCHP系统发展的主流趋势，面向屋顶、停车棚的光伏发电系统是其中最主要的应用形式之一，适用于多数场景。典型CCHP系统如图1所示，其中：燃气机组发电功率Ppgu、光伏发电功率Ppv、电网功率Pgrid共同组成用户电负荷需求Pload的供给端；燃气机组发电过程会产热，利用余热回收系统可以回收热功率Prec，并与燃气锅炉产生的热功率Pb共同作为用户热负荷需求Pheat的供给端；而冷负荷Pac可由电制冷机和吸收式制冷机联合提供；绿色、红色、蓝色线条分别表示电能、热能、冷能的流动。

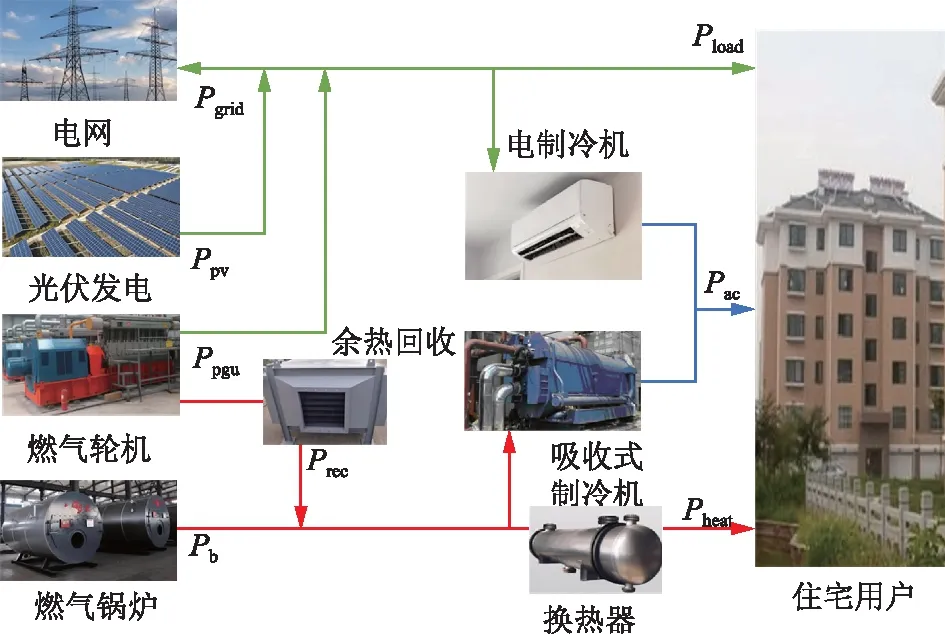
图1 典型CCHP系统结构Fig.1 Typical CCHP system structure

CCHP系统与电网之间有不并网、并网不上网、并网且上网3种模式。并网即CCHP系统连接至电网，两者共同满足用户的电负荷需求；上网即当CCHP系统产生的电能仍然有剩余时，能够反向售电给电网，并获取一定收益。在无蓄电池的CCHP系统中，并网且上网模式一方面使得设备控制更加灵活，另一方面也可以降低系统运行成本，因此成为CCHP系统的发展趋势；但由于各地并网上网政策、售电价格等的差异较大，目前大部分实际案例未有效考虑上网过程的相关因素。鉴于并网且上网模式的优势以及CCHP系统发展的需求，本文研究以并网且上网作为系统的基本运行模式，重点考虑能源消耗指标对CCHP系统运行控制策略的影响，旨在提高系统综合能源利用效率，降低碳排放量和运行成本。

2 CCHP系统控制策略

CCHP系统的运行控制是一个多变量、多约束、多目标问题，需要综合考虑负荷波动、设备效率、运行成本、环境指标等多个因素，调度模型较为复杂。对于CCHP系统的运行控制策略，一方面需要保证用户电、冷、热负荷需求得到满足，另一方面需要综合考虑多个因素耦合影响下的优化问题。

2.1 基于规则的控制策略

传统“以电定热”或“以热定电”的控制策略均属基于规则(rule-based，RB)的控制策略之一。RB控制策略实施简单，可通过设定具体判据(如系统运行费用、能源利用效率、污染物排放等)进行系统控制。考虑到在并网且上网模式下，可以通过电网调控实现CCHP系统电能的实时平衡，“以电定热”控制策略更加灵活，有利于发挥燃气机组的效率优势，而如何结合售电价格实现系统运行成本最小化，则是该运行控制策略的重要考量指标。

CCHP系统的上网售电价格，根据时段不同可分为高售价、平售价和低售价3个区间，根据上述目标，通过将上网售电价格和“以电定热”控制方式相结合，提出并网且上网模式下CCHP系统的RB控制策略。规则如下：

①在高售价时段，燃气机组以最大发电功率运行，在满足用户电负荷需求的情况下，若有多余电量将全部上网售电。

②在平售价时段，燃气机组优先满足电负荷需求，在此基础上，充分考虑系统冷热负荷所对应的热能需求，并以该热能需求确定燃气机组的输出功率，该工况下控制策略类似于传统“以热定电”模式。

③在低售价时段，电网购电价格一般也较低，此时CCHP系统主要通过电网购电方式运行，燃气机组仅维持最低输出功率运行。

基于上述控制规则，得到CCHP系统的RB控制策略判断步骤如图2所示。

图2 基于规则的控制策略流程Fig.2 RB control strategy flow chart

燃气机组产生的热能通过余热回收机组回收，并通过换热器和吸收式制冷机组提供用户所需的热负荷和冷负荷，不足部分由燃气锅炉补充。而在该系统拓扑架构下，冷负荷50%由电制冷机提供，该部分能量等效转化为电负荷；另外50%由吸收式制冷机组提供，等效转化为热负荷。由此，可以得到t时刻最终需要生产的新电负荷Pnload(t)与新热负荷Pnheat(t)分别为：

(1)

(2)

式中：Pload(t)、Pheat(t)、Pcold(t)分别为t时刻用户所需的电负荷、热负荷与冷负荷；σec为电制冷机的能效比；ηab为吸收式制冷机的转换效率；ηeheat为换热器换热效率。

2.2 基于NSGA-Ⅱ的控制策略

由于不同的CCHP系统具有不一样的特征，且各地上网售电价格也不尽相同，上述RB控制策略更适用于特定系统，其控制方法不具备普适性和移植性，需要根据不同的CCHP系统进行特定的判据分析。智能算法可以解决规则算法的问题，通过算法中的基本搜索单元实现不同系统控制策略的智能优化，具有更好的应用价值。智能算法包括遗传算法、粒子群算法、深度学习等，考虑到系统复杂性、算法实时性和收敛性以及硬件成本等因素，本文采用NSGA-Ⅱ算法实现CCHP控制策略优化[23]。

NSGA-Ⅱ是一种改进型遗传算法，其选择、交叉和变异环节仍保持遗传算法的特点，但在选择算子执行前，则根据个体之间的支配关系进行分层。由于选择算子可以利用个体组成的解集间存在的支配与非支配关系，对种群进行层数分割，因此能够支配的解将处于高等级层数内，而被支配的解处于低等级层数内，且同一层内解集互不支配；非支配层数越高的个体被选择概率越大，由此可以保证解的多样性，并使个体能均匀分布在Pareto前沿。

在本文实际执行过程中，NSGA-Ⅱ算法采用拥挤度实现策略上的优化，计算每个个体与其相邻的2个个体在每个子目标函数上的距离差之和，求取其拥挤距离。在本文中，2个目标函数具备相同的权重，累加二者的拥挤度，同时考虑个体在子目标函数的表现，能够有效优化程序运行。此外，在初始化过程生成种群时，增加了代入约束条件进行判断的环节，能够有效减少错误解的生成，达到对种群的初步筛选，以此改进NSGA-Ⅱ算法。改进型NSGA-Ⅱ算法通过观测个体对各约束条件的违反情况，经过叠加及归一化处理，可以对违反约束条件系数较大的个体给予更低的Pareto等级，减小其被选择的概率，从而优化算法的整体迭代搜索过程。改进型NSGA-Ⅱ算法的流程如图3所示。

图3 NSGA-Ⅱ算法流程Fig.3 NSGA-Ⅱ algorithm flow chart

步骤1，初始化当前等级下所有个体的拥挤度P(i)=0，其中i为个体。

步骤2，遍历所有个体和对应的目标值，根据该目标函数对该等级中的个体进行排序。

步骤3，将个体排序后的2个边界值的拥挤度置为∞，即P(1)=∞，P(N)=∞，其中N为种群最大数量。

2.3 目标函数

CCHP系统运行控制受到诸多因素的影响，同时存在多个相互对立的优化目标，如一次能源利用率、运行成本、投资成本、污染物排放量等，各个目标又包含各自的子模块或参数，如运行成本包含了各个单元消耗的燃料费用、各设备的运行维护费用、设备投资折旧成本、与外部电网交互(购电或售电)的收益等。因此，利用NSGA-Ⅱ算法解决CCHP系统优化控制问题，还应建立各个目标的数学模型，获得相应的目标函数。

本文CCHP系统优化控制策略以运行成本和燃料消耗量作为双重优化目标，一方面考虑CCHP系统运行成本费用的最小化，包括燃气机组发电与维护费用、有害污染物处理排放费用、电网交互费用和燃气锅炉燃料费用，另一方面也需要减少一次能源消耗量以降低综合能源系统的总体碳排放量，其可由天然气消耗量以及等效煤炭消耗量来表示。

根据上述分析，CCHP系统t时刻运行费用由4个部分组成，分别为t时刻的燃料费用ffuel(t)、运行维护费用fm(t)、污染物处理费用fenv(t)、电网交互费用fex(t)，计算式分别如下。

(3)

式中：CL为天然气单价；ηt、ηb分别为燃气机组和燃气锅炉的功率系数；PMT(t)、PB(t)分别为t时刻燃气机组和燃气锅炉的功率。

fm(t)=FMTPMT(t)+FBPB(t)+

FPVPPV(t)+FABPAB(t).

(4)

式中：FMT、FB、FPV、FAB分别为燃气机组、燃气锅炉、光伏发电和吸收式制冷机的运行维护费用单价；PPV(t)、PAB(t)分别为t时刻光伏发电和吸收式制冷机的功率。

fenv(t)=μCO2，g(PMT(t)+PB(t))+

μCO2，e|Pgrid(t)|.

(5)

式中：μCO2，g为燃气产生二氧化碳的系数；μCO2，e为电网供电所产生的二氧化碳系数；Pgrid(t)为t时刻电网供或购电功率。

(6)

式中fb(t)、fs(t)分别为t时刻购电价格与售电价格。

由此得到t时刻CCHP系统的总运行成本

Ftotal(t)=ffuel(t)+fm(t)+fenv(t)+fex(t).

(7)

此外，t时刻燃料消耗总量Ffossil主要由燃气锅炉和燃气机组2部分组成，如下：

(8)

根据上述目标函数，由于在考虑Pareto最优解集的NSGA-Ⅱ算法中，不需要对各目标函数设置特定的权重，也即NSGA-Ⅱ算法自动搜索最优解集的过程不依赖于目标函数权重值，系统目标函数可表示为：

minF=Ftotal(t)⊕Ffossil(t).

(9)

2.4 约束条件

目标函数的优化过程受到各参量相互关系、运行边界条件等的限制，因此需要建立相关约束条件，使得算法搜索过程排除不符合系统需求的解集。根据图1的CCHP系统拓扑结构，可以得到保持系统正常运行的平衡约束条件和不平衡约束条件。

电力供需平衡是保证CCHP系统正常运行的首要约束条件，当电功率不平衡时，易造成频率不稳定，进而影响系统的稳定性。因此，建立电功率平衡约束条件如下：

Pnload(t)=PMT(t)+Pgrid(t)+PPV(t).

(10)

其次，系统的热能也需要满足平衡约束条件，即产生的热能等于消耗的热能；而若某时刻存在多余热能，则需要综合考虑浪费的热能。因此，建立热能平衡约束条件如下：

Pnheat(t)=PB(t)+Prec(t)-Pwaste(t).

(11)

式中；Prec(t)为t时刻燃气机组余热回收的热流量；Pwaste(t)为t时刻浪费的热流量。

此外，各单元的设备都受到硬件条件限制，需要处于一定的工作区间。因此，可列出燃气机组、燃气锅炉等控制单元输出功率的约束条件，如式(12)、(13)所示：

PMT，min≤PMT(t)≤PMT，max；

(12)

PB，min≤PB(t)≤PB，max.

(13)

式中：PMT，min、PMT，max分别为燃气机组的最低运行功率和最高运行功率；PB，min、PB，max分别为燃气锅炉的最低运行功率和最高运行功率。

3 算例分析

3.1 基础数据

本算例以广东省某宾馆CCHP系统夏季典型日作为研究对象，该宾馆CCHP系统采用并网且上网的运行模式，其逐时电、热、冷负荷以及屋顶光伏发电系统发电量如图4所示。单位时间间隔Δt=1 h，调度时间周期T=24 h。

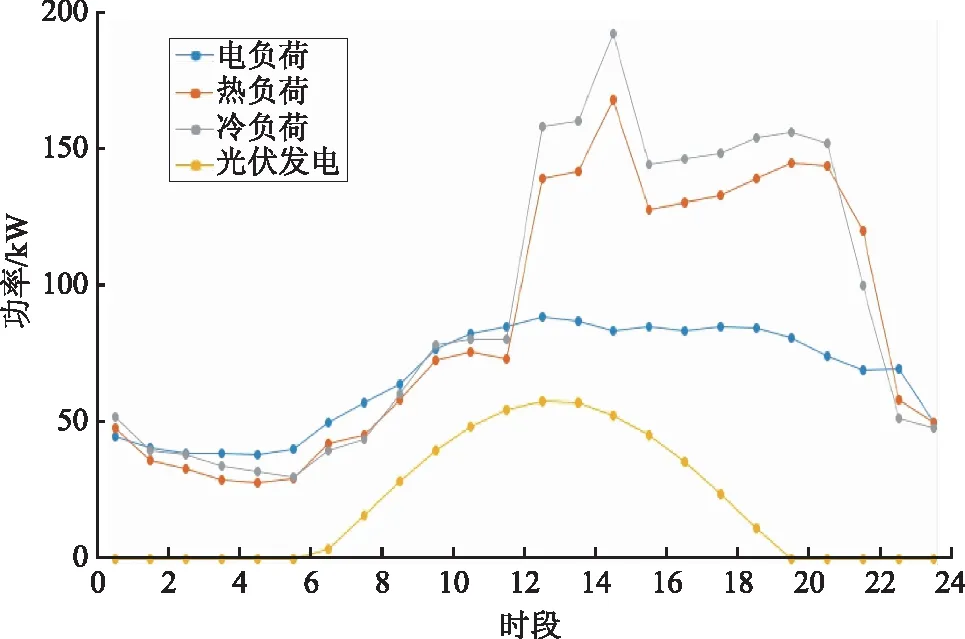
图4 用户负荷及光伏发电曲线Fig.4 User’s load and PV generation curves

由图4可知：用户电负荷需求峰值为88.66 kW，平均值为66.75 kW；热负荷需求峰值为167.76 kW，平均值为81.10 kW；冷负荷需求峰值为192.27 kW，平均值为92.45 kW；光伏系统以最大功率跟踪点运行，光伏发电峰值为57.68 kW，平均值为19.76 kW。由于本案例以小时为单位，未充分考虑光伏发电短时的波动和间隙性，均统一折算至单位时间内。

该系统采取的电价费用实行峰段、平段、谷段三段式电价政策，且购电电价段和售电电价段一致。其中，第0至第6时段、第23时段为谷段用电时间，第7至第9时段、第14至16时段和第22时段为平段用电时间，第10至第13时段、第17至第21时段为峰段用电时间。购电价格与售电价格见表1。

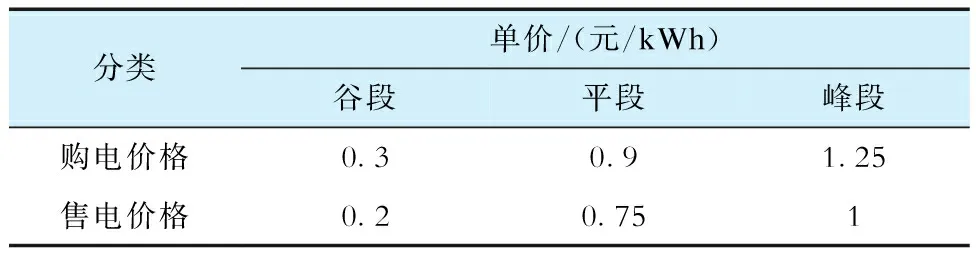
表1 各时段购售电价格Tab.1 Electricity purchase and sale prices for each time period

对于NSGA-Ⅱ算法来说，最重要的3个环节是遗传、交叉和变异，在交叉环节和变异环节需要分别设置交叉概率和变异概率。本文NSGA-Ⅱ算法相关参数设定包括：种群规模为50个个体，最大迭代次数500，交叉概率0.7，变异概率0.05。

惩罚元素则通过程序中的约束条件进行判断。在程序运行过程中，将变量设置在合理的区间内，对于违反约束条件的个体，依据种群个体违反程度，采取降低Pareto等级的方式，使其排在种群较后的位置，以最大限度避免选取这一类个体。此外，该系统的主要排放物为二氧化碳、二氧化硫以及氮氧化物，处理单价分别为0.210 元/kg、14.842元/kg和62.964元/kg。表2、表3分别给出了各单元的排放系数以及各发电单元特性参数。

表2 各单元排放系数Tab.2 Emission coefficient of each unit

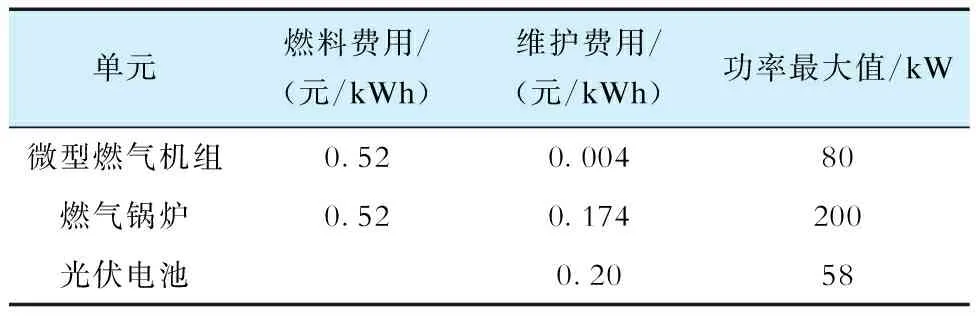
表3 各单元运行维护费用Tab.3 Operation and maintenance cost for each unit

3.2 仿真结果分析

利用MATLAB软件对CCHP系统的RB控制策略和NSGA-Ⅱ控制策略进行算法编程，通过导入该宾馆以及算法的基础数据进行仿真分析，得到该宾馆夏季典型日RB控制策略和NSGA-Ⅱ控制策略中各设备单元的逐时功率调度情况，分别如图5、图6所示。

图5 RB控制策略调度曲线Fig.5 Dispatch curves of RB control strategy

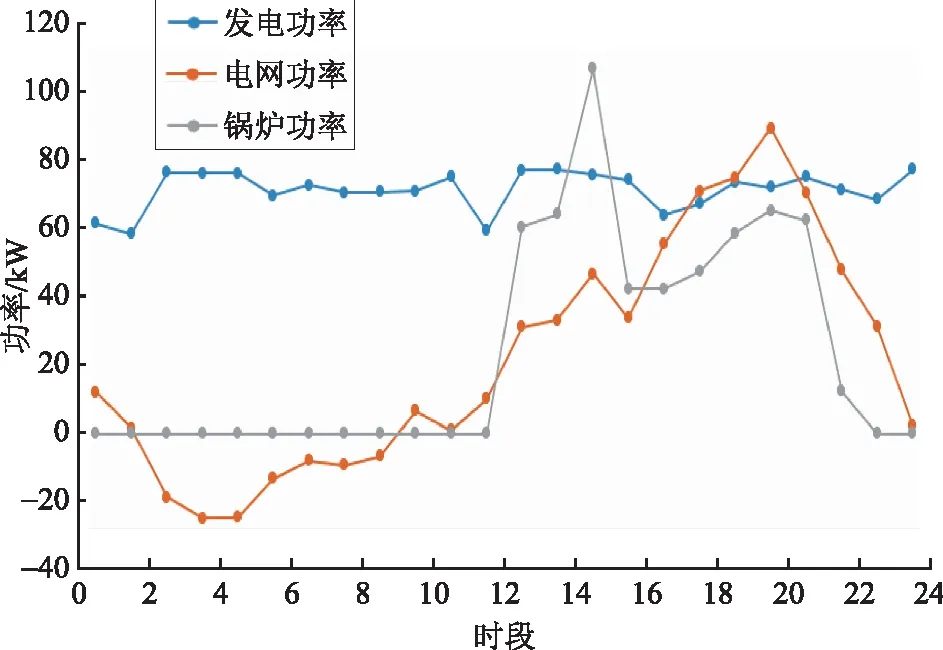
图6 NSGA-Ⅱ控制策略调度曲线Fig.6 Dispatch curves of NSGA-Ⅱ control strategy

对比图5和图6可知：在第1至7时段中，RB控制策略将燃气机组按最低运行功率运行，电网在这段时间为供电主力；而在第8至10时段、第15至17时段以及23时段中，燃气机组与电网共同为用户提供电能；在其余时段中，燃气机组作为用户供电的主力，不足时再通过电网补充。对于NSGA-Ⅱ控制策略，燃气机组均没有运行在最低功率下，在第1至7时段，以燃气机组为供电主力，多余的电量出售给电网；在其余大部分时段，燃气机组均以较高的功率运行，并辅以电网提供部分电负荷；而在12、19、20以及23时段中，电网购电功率均大于燃气机组功率，原因是在这3个时间段中，冷、热负荷所需要的能量由燃气锅炉提供，相较于通过燃气机组产能以提供余热，前者更加具有经济性。

图7、图8分别为2种控制策略下的逐时成本对比和逐时燃料消耗量对比。从图7可以看出：在谷电价时段，NSGA-Ⅱ所花费的运行成本相比RB控制策略高一些，而其他时间段均低于RB控制策略或者持平。从图8可以看出：NSGA-Ⅱ所得到的逐时能源消耗普遍低于RB控制策略所得到的逐时消耗，也即运行过程中整体碳排放量较低，这得益于NSGA-Ⅱ充分利用电网对CCHP系统进行调控，在电价较低时段尽可能购电来满足用户电负荷需求；冷、热负荷则通过燃气机组提供，并辅以燃气锅炉进行补充。

图7 逐时成本对比Fig.7 Hourly cost comparisons

图8 逐时燃料消耗对比Fig.8 Hourly fuel consumption comparisons

燃气机组的负载率是衡量CCHP系统一次能源利用率的重要参数，2种控制策略下的燃气机组效率如图9所示。由图9可以看出：在NSGA-Ⅱ控制策略下，燃气机组的负载率保持在70%～100%之间，处在一个相对平稳且高负载率的工况中；在RB控制策略下，燃气机组在谷段以最低负载率运行，在峰段以最高负载率运行。通过比较可知，在NSGA-Ⅱ控制策略下的燃气机组运行工况更加平衡，有效减少了燃机机组运行过程的波动。

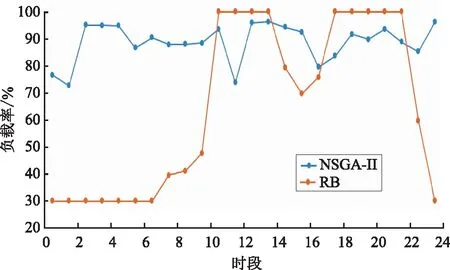
图9 燃气机组负载率对比Fig.9 Gas turbine load rate comparisons

分别按照RB算法和NSGA-Ⅱ算法得出系统的运行控制策略后，可以得到CCHP系统夏季典型日运行总费用及总燃料消耗，具体数值见表4。

表4 2种策略调度结果Tab.4 Scheduling results of two strategies

由表4可以看出：在日运行成本上，NSGA-Ⅱ算法所得出的运行控制策略相比RB算法减少了6.63%；在能源消耗上，NSGA-Ⅱ算法的消耗量比RB算法减少了31.58%，系统低碳运行效果更加显著。因此，NSGA-Ⅱ算法得到的运行控制策略在降低碳排放和运行成本方面均具有较大的优势，更适用于该CCHP系统。

此外，在迭代过程中，采用误差函数实现算法收敛性检测。误差函数的计算公式如下：

(17)

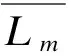
图11 迭代曲线Fig.11 Iterative curve

4 结束语

本文研究了并网且上网模式下，配有燃气机组、光伏发电以及燃气锅炉等设备的电-气综合CCHP系统的运行策略，分别使用RB算法和NSGA-Ⅱ算法对系统控制策略进行求解。根据仿真结果得出结论，将Pareto方法与遗传算法相结合所形成的NSGA-Ⅱ算法得出的运行控制策略，比基于RB算法的控制策略具备更好的适应能力，且系统的调度结果也不会受到人为偏好的影响。在降低系统碳排放量和运行成本方面，NSGA-Ⅱ算法所得到的运行控制策略体现出更好的调度效果，可以更好地推广应用到CCHP系统中。