基于多模型加权调度的锅炉过热汽温广义预测串级控制

胡宇航，徐振华，王林，程功，刘锦廉，朱策

(国网福建省电力有限公司电力科学研究院，福建 福州 350007)

现阶段，在火电厂自动控制系统中，主要采用串级比例-积分-微分(proportion-integral-derivative，PID)控制器的方法来调节过热汽温。PID控制器有一定的鲁棒性，在工程方面应用较多；但对于大惯性、大迟延、多扰动的锅炉过热汽温系统，要确定最优的PID控制参数比较困难，致使PID控制器往往不能满足控制系统的要求，在变工况运行时常出现超调和振荡现象。

近年来，在过热汽温控制方面采用先进控制和智能控制方法成为一种新的趋势。文献[1]提出一种高阶抗扰控制方法，运用于某电厂过热汽温调节系统的优化，相对PID控制器在抗扰性能上具有良好的优势；文献[2]提出一种基于动态矩阵控制(dynamic matrix control，DMC)的过热汽温预测控制策略，根据过热蒸汽传输通道特性，将减温水流量扰动作为前馈补偿，很大程度改善了过热汽温控制系统动态和稳态性能；文献[3]提出一种DMC与自抗扰控制结合的串级控制方法，具有更加优良的设定值跟踪能力和鲁棒性；文献[4]提出了一种基于神经网络前馈补偿的在线自适应非线性预测控制算法。采用高阶惯性环节加神经网络补偿的混合非线性模型，作为预测模型代替传统的可控自回归积分滑动平均模型，对于某些非线性被控对象具有良好的跟踪品质。文献[5]提出一种基于隐式广义预测控制(generalized predictive control，GPC)的过热汽温预测控制策略，将隐式GPC控制器加入到过热汽温串级控制系统的主回路中，将减温水部分产生的扰动作为前馈补偿，提高了控制系统的鲁棒性；文献[6]选取过热汽温作为被控对象，采用DMC和GPC 2种典型预测控制算法分别对其进行控制，发现增益失配比例在一定范围内，GPC可以迅速使系统达到平衡，另外在时间常数失配的情况下，DMC比GPC具有更好的适应性；文献[7]提出一种基于间接能量平衡的锅炉汽温GPC-PID串级控制，能明显地改善过热汽温的控制效果。

在实际机组运行过程中，随着负荷工况的变化，喷水量与过热汽温间的特性关系随之发生改变，在机组大范围变工况运行时，依靠单一模型的过热汽温预测控制，原控制参数并不适配，会导致控制性能退化[8]。

本研究根据典型负荷工况建立模型子集，采用自适应加权系数构建多模型广义预测串级控制器(以下简称为“GPC-PI控制器”)：主回路采用GPC控制器来控制过热汽温，将控制输出作为副回路的设定值；副回路采用PI控制器，控制导前区温度。在MATLAB/Simulink环境下验证控制策略的鲁棒性和有效性。

1 过热汽温控制系统特性

典型过热蒸汽喷水减温系统如图1所示，图中θ1为导前区汽温信号，θ2为过热汽温，W1为一级减温水流量，W2为二级减温水流量。

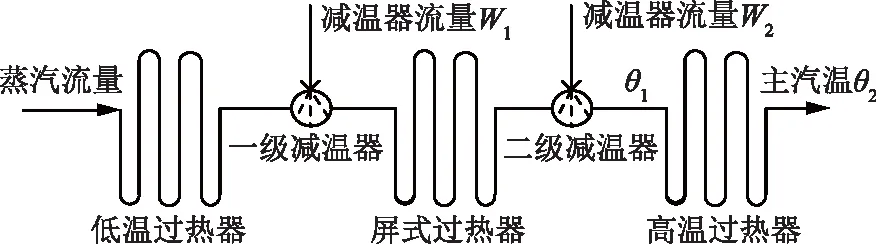
图1 过热蒸汽喷水减温系统Fig.1 Water spray desuperheating system of superheated steam

一级减温器和二级减温器在运行中保护屏式过热器和高温过热器，防止超温，同时调节左、右侧汽温的偏差，使主蒸汽温度维持在额定值。各减温水的控制要平稳，温度控制要超前，避免调节阀突开、突关造成过热器壁温急剧变化，影响受热面的使用寿命[9]。

目前大多数机组的过热汽温采用串级PID控制，控制模型如图2所示，图中G1(s)为导前区的传递函数，G2(s)为惰性区的传递函数，D1(s)、D2(s)为外部扰动[10]，s为拉普拉斯算子。

图2 过热汽温串级PID控制模型Fig.2 Cascade PID control model of superheated steam

导前区的传递函数模型为

(1)

惰性区的传递函数模型为

(2)

式(1)、(2)中：K1、K2为传递函数的增益系数；T1、T2为传递函数的惯性时间常数；n1、n2为传递函数的阶次。

某超临界直流锅炉高温过热器典型负荷下，将K1、K2、T1、T2、n1、n2这些参数的数值代入式(1)、(2)中，可得喷水量扰动时的过热汽温动态特性，见表1[11]，其中P为机组负荷，Pn为机组额定负荷。

表1 喷水量扰动时的过热汽温动态特性Tab.1 Dynamic characteristics of superheated steam temperature in water spray disturbance

由表1可以看出，过热汽温在各个负荷工况下特性差异较大，负荷越低，过热汽温对喷水量的响应惯性越大，整体增益越强。依赖一套PID参数很难达到好的控制效果，且大惯性、大迟延、非线性的特性也加大了PID参数的整定难度。

另一方面，由于选型不当、安装工艺，或长期使用的阀芯被磨损、汽蚀等原因，许多减温水调节阀的开度-流量特性存在非线性特性，这也是影响汽温调节的重要原因。文献[12]通过分散式控制系统(distributed control system，DCS)历史数据对减温水调节阀开度和流量进行拟合，得出阀门流量特性函数，见表2。在20%以下开度时，开度变化1%引起减温水流量W的变化约为0.6%Wmax(Wmax为最大流量)；50%～70%开度时，开度变化1%时W变化量约为2.1%Wmax，是20%以下开度时W变化量的3.5倍。研究发现在PID控制器出口增加阀门流量补偿函数，进行阀门流量特性校正，再经手/自动操作器后输出指令控制调节阀开度，可提高过热汽温调节品质。

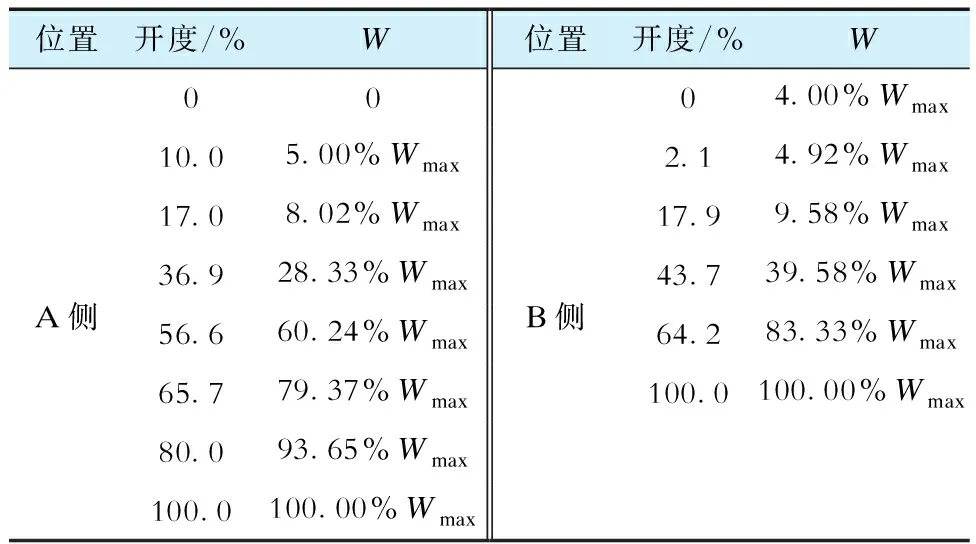
表2 A、B侧减温水调节阀开度-流量拟合函数Tab.2 Fitting function of opening-flow rate of side A、B desuperheating water regulating valve

2 过热汽温广义预测串级控制策略

本研究采用表1所示传递函数为例设计过热汽温GPC-PI控制器，原理图如图3所示。其中GPC1—GPC4分别为100%、75%、50%、37%额定负荷下根据模型辨识所设计的子控制器。u1—u4分别为各子控制器根据过热汽温设定值ω以及实际过热汽温所得的最优控制输出。调度控制器根据负荷指令信号以及设计好的隶属度函数规则进行权重的分配，确定每个子控制器输出所占的权重w1—w4，最终通过将各子系统的输出相累加，构成GPC控制器的实际输出u，其进入副回路作为导前区温度的设定值(副回路的输入)。副回路采用常规PI控制器，y为被控对象过热汽温(副回路的输出)。

2.1 GPC预测模型

GPC的预测模型为可控自回归积分滑动平均模型，此模型可以写成

A(z-1)y(k)=B(z-1)u(k-1)+C(z-1)ξ(k)/Δ.

(3)

其中：

1+a1z-1+a2z-2+…+anz-n，

(4)

b0+b1z-1+b2z-2+…+bmz-m，

(5)

1+c1z-1+c2z-2+…+cnz-n.

(6)

式(3)中：A(z-1)、B(z-1)、C(z-1)分别为n、m、n阶后移算子z-1的多项式；Δ=1-z-1为差分算子；ξ(k)为时刻k副回路的白噪声。为了简化，可令C(z-1)=1[13]，则式(3)可写为

A(z-1)Δy(k)=B(z-1)Δu(k-1)+ξ(k).

(7)

令

θ=(a1，…，an，b0，…，bm)T.

(8)

φ(k)=(-Δy(k-1)，…，-Δy(k-n)，

Δu(k-1)，…，Δu(k-m-1)).

(9)

则

Δy(k)=φT(k)θ+ξ(k).

(10)

采用渐消记忆的递推最小二乘法估计参数向量[14]，即可得到多项式A(z-1)和B(z-1)的参数。

将图3中副回路PI控制器比例系数设为0.4，积分增益设为0.01。在GPC控制器输出u处施加阶跃量5 ℃，得到过热汽温的响应量。选择采样周期为3 s，多项式A(z-1)和B(z-1)的阶次为8阶，采用递推最小二乘法求得GPC的对象模型参数，见表3，其中A1—A4分别为100%Pn—37%Pn工况下的多项式A(z-1)的系数向量，B1—B4分别为100%Pn—37%Pn工况下的多项式B(z-1)的系数向量。

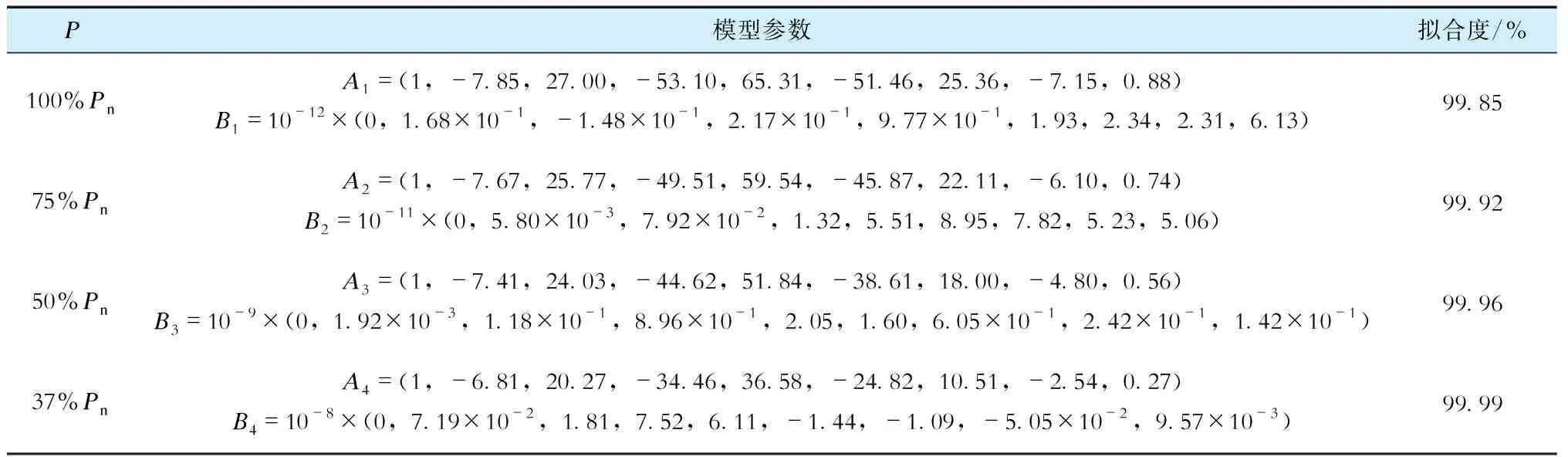
表3 GPC模型参数辨识结果Tab.3 Parameter identification results of GPC model

模型阶跃响应曲线如图4所示。

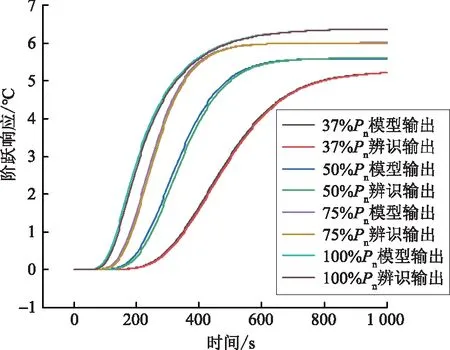
图4 模型阶跃响应曲线Fig.4 Model step response curve

2.2 输出预测

引入丢番图(Dioaphantine)方程

1=Ej(z-1)A(z-1)Δ+z-jFj(z-1).

(11)

其中Ej(z-1)、Fj(z-1)均为由A(z-1)和预测长度j唯一确定的多项式，

Ej(z-1)=ej，0+ej，1z-1+…+ej，j-1z-(j-1).

(12)

Fj(z-1)=fj，0+fj，1z-1+…+fj，nz-n.

(13)

由式(3)和式(11)可得

y(k+j)=Ej(z-1)B(z-1)Δu(k+j-1)+

Fj(z-1)y(k)+Ej(z-1)ξ(k+j).

(14)

令

Gj(z-1)=Ej(z-1)B(z-1)=

(15)

再引入另一丢番图方程

Gj(z-1)=G′j(z-1)+z-(j-1)Hj(z-1)，

(16)

其中多项式G′j(z-1)、Hj(z-1)分别为：

(17)

Hj(z-1)=hj，1z-1+hj，2z-2+…+hj，mz-m.

(18)

不计未来噪声的影响，则有

Hj(z-1)Δu(k)+Fj(z-1)y(k).

(19)

式中p为不计未来噪声的最佳预测值。

2.3 滚动优化

GPC为一种在线寻优算法，此算法的每个控制时步都会由当前已知的输入、输出信息执行1次寻优计算，即滚动优化[15]。

2.3.1 性能指标

在GPC中，k时刻的优化性能指标

(20)

ys(k+j)=ays(k+j-1)+(1-α)ω，

(21)

式(20)、(21)中：E为数学期望；ys为对象输出的期望值；λ为控制加权系数；N为优化时域；Nu为控制时域，即在Nu步后控制量不再变化；α为柔化因子。

2.3.2 最优控制律

令

y(k|k)=(p(k+1|k)，…，p(k+N|k))T，

(22)

Δu(k|k)=

(Δu(k|k)，…，Δu(k+Nu-1|k))T，

(23)

ω(k)=(ys(k+1)，…，ys(k+N))T，

(24)

且用p(k+j|k)代替式(20)中的y(k+j|k)，则性能指标写成向量形式，即

J(k)=(y(k|k)-ω(k))T×

(y(k|k)-ω(k))+Δu(k|k)TλΔu(k|k).

(25)

Δu(k|k)=(λI+GTG)-1GT×

(ω(k)-F(z-1)y(k)-H(z-1)Δu(k)).

(26)

其中：

F(z-1)=(F1(z-1)，…，FN(z-1))T，

(27)

H(z-1)=(H1(z-1)，…，HN(z-1))T.

(28)

实际控制时，控制系统每次只取第1个分量，即

u(k)=u(k-1)+

dT(ω(k)-F(z-1)y(k)-H(z-1)Δu(k)).

(29)

式中dT为矩阵(λI+GTG)-1GT的第1行。

2.4 多模型高斯隶属度加权调度

多模型切换有硬切换和软切换2种策略[16]。硬切换依据某一性能指标(如输出误差指标、估计误差指标、反馈误差指标等)，通过实时计算性能指标，选取性能指标最小的控制器参与调节。由于切换过程中在不同控制之间选择，硬切换控制输出有可能出现跳变[17-18]。在机组实际运行中，减温水流量、主蒸汽流量、总燃料量的变化都会引起过热汽温的变化。受干扰因素影响，基于过热器减温水流量设计的单变量预测控制器，未必能根据误差性能指标匹配到最优的子控制器[19]。

本研究采用基于高斯隶属度函数的输出加权策略来实现多模型软切换。软切换通过改变各个控制器输出权值，来适应变负荷过程中对象模型的变化，切换过程中系统影响较小。

高斯Gaussian隶属度函数

(30)

式中：fi为各个子控制器在不同负荷指令下的高斯隶属度；x为负荷指令标幺值；bi为各个子控制器的高斯隶属度的中心，分别为0.37、0.5、0.7、1.0；σi为高斯隶属度函数的宽度参数。

当负荷指令位于相邻典型工况中间位置时，取相邻子控制器的隶属度为0.5，则得出σ1、σ3、σ4为0.055 2、0.106 2、0.106 2。σ2在x<0.5时取值0.055 2，在x≥0.5时σ2取值0.106 2。

高斯隶属度函数如图5所示。

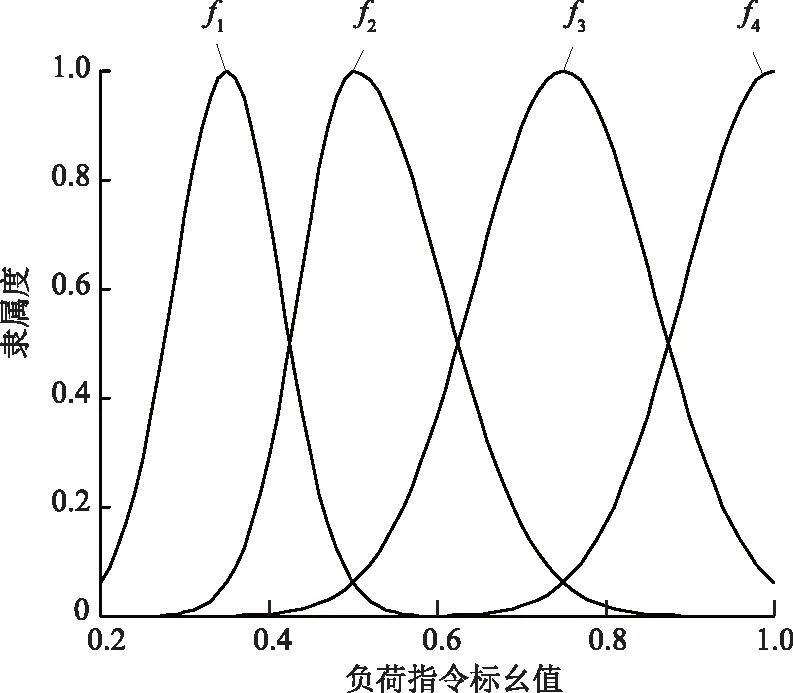
图5 高斯隶属度函数Fig.5 Gaussian membership function

各子控制器的输出加权系数

(31)

GPC控制器输出即由各子控制器的输出与加权系数相乘后求和而得。

2.5 输出约束

控制器的设计过程中必须同时考虑控制作用的物理限制，所以需要对控制器输出进行约束[20-21]。

设umax、umin为控制量的上、下限幅值，将式(29)改为增量形式，即

u(k)=u(k-1)+Δu(k)，

(32)

则有

umin-u(k-1)≤Δu(k)≤umax-u(k-1).

(33)

设Δumax、Δumin为控制量变化速率的上、下限值，则有

Δumin≤Δu(k)≤Δumax.

(34)

为了防止GPC控制器输出在减温水调节阀到达全关位或全开位后，仍继续向上或向下输出，造成“饱和”现象，导致回调不及时，故当副回路输出接近下限或上限时，GPC控制器输出应相应闭锁增减。

结合式(33)与式(34)，记减温水调节阀开度为v，得到控制增量Δu(k)的约束范围为：

(35)

3 仿真研究

3.1 控制器参数整定

本研究设计的GPC控制器参数如下：采样周期为3 s，预测长度为120，控制长度为1，控制加权系数为50，柔化系数为0.96，控制量速率约束为每个周期±2 ℃，控制量范围约束为±30 ℃。

为了比较GPC控制器与常规串级PID控制器的控制效果，在MATLAB/Simulink环境下构建常规串级PID控制回路，采用MATLAB/Simulink的PID参数自整定功能求得不同负荷段下主回路PID控制器的比例增益及积分增益，见表4。副回路控制器的控制参数与GPC-PI控制器的副回路参数一致。

表4 常规串级PID控制器参数整定值Tab.4 Parameter setting values of conventional cascade PID controller

3.2 单一工况下考虑减温水调节阀特性的预测控制及常规串级控制效果

根据表2中A侧调节阀的数据，以减温水调节阀开度v为自变量，减温水流量W为因变量，进行三次曲线的拟合，拟合后可得到三次方程

W=-0.000 26v3+0.039v2-0.3v+1.9.

(36)

记单位减温水流量对单位调节阀开度的增益系数为R，

R=ΔW/Δv.

(37)

对式(36)进行求导，即可得到R与v的关系为

R=-0.000 78v2+0.078v-0.3.

(38)

以30%调节阀开度为基准，使用由式(38)所得R值修正不同开度下增益系数，检验GPC对变增益的鲁棒性。副回路修改后如图6所示。

图6 考虑减温水流量特性的副回路Fig.6 Secondary circuit consideringflow characteristics of desuperheating water

在37%、50%、75%、100%额定负荷下，分别采用对应的模型参数设计的GPC1—GPC4及常规串级PID控制器，对过热汽温设定值进行±5 ℃的阶跃扰动，扰动过程如图7—图10所示，其中GPC控制器输出为导前区的温度设定值。

图7 37%额定负荷工况下过热汽温设定值扰动曲线Fig.7 Disturbance curves of superheated steam temperature setting values under 37% rated load condition

图8 50%额定负荷工况下过热汽温设定值扰动曲线Fig.8 Disturbance curves of superheated steam temperature setting values under 50% rated load condition

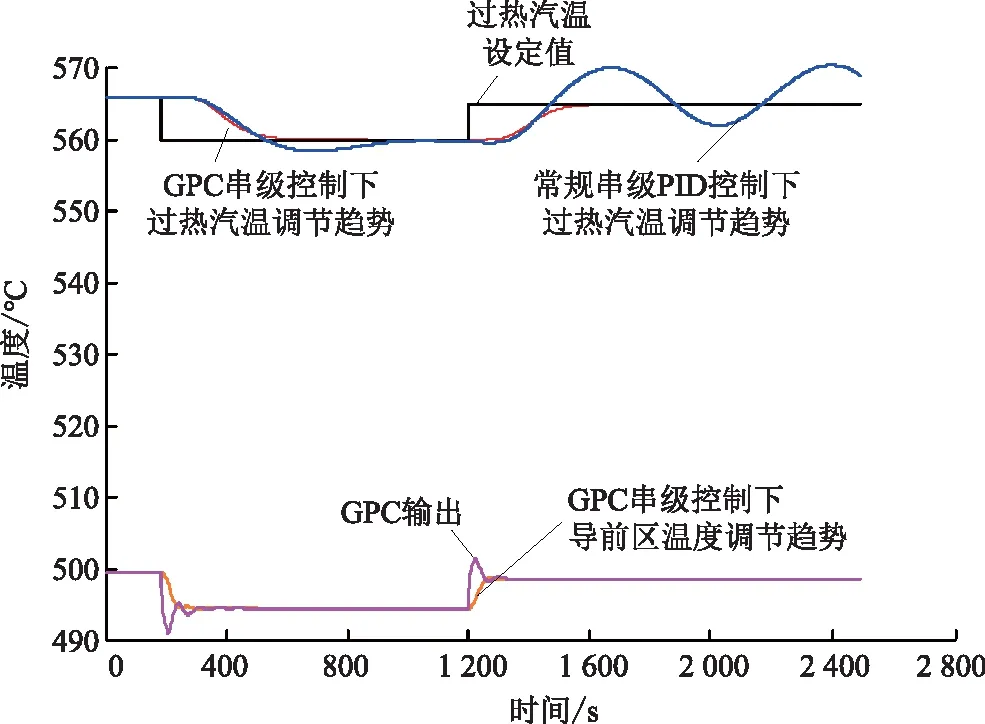
图9 75%额定负荷工况下过热汽温设定值扰动曲线Fig.9 Disturbance curves of superheated steam temperature setting values under 75% rated load condition

图10 100%额定负荷工况下过热汽温设定值扰动曲线Fig.10 Disturbance curves of superheated steam temperature setting values under 100% rated load condition

从图7—图10中可以看出，单一工况下考虑减温水调节阀特性的GPC-PI控制器能够快速、稳定地控制过热汽温，其对增益失配具有一定的鲁棒性。随着负荷的降低，过热汽温对减温水的响应特性呈现惯性时间越来越大的趋势，因此37%Pn的过热汽温调节时间比其他负荷的调节时间较长；但最大超调量控制在2 ℃左右，满足实际控制要求。

在过热汽温设定值向下阶跃扰动时，常规串级PID控制器能够较为快速稳定住被调量；但在过热汽温设定值向上阶跃扰动时调节不稳，甚至出现振荡的趋势。由于GPC-PI控制器采用输出预测、滚动优化的机制，相较于常规串级PID控制器“事后调节”的机制，表现出了更优的调节性能。

3.3 变负荷工况下预测控制效果

将表1中惰性区传递函数统一等价为7阶传递函数，以表1中典型工况的导前区增益、导前区惯性时间、惰性区增益、惰性区惯性时间为基点，进行曲线拟合，构建37%Pn—100%Pn全过程喷水量扰动时的过热汽温动态特性，在仿真环境检验变负荷工况下预测控制的效果。负荷指令以1.5%Pn/min的速率从50%Pn升至100%Pn，其间对过热汽温设定值进行-5 ℃的扰动，分别以固定模型参数设计的GPC-PI控制器以及多模型加权调度GPC-PI控制器来调节过热汽温，调节趋势如图11、图12所示。图11中固定模型参数2—4分别对应表3中50%、75%、100%额定负荷下的模型参数。

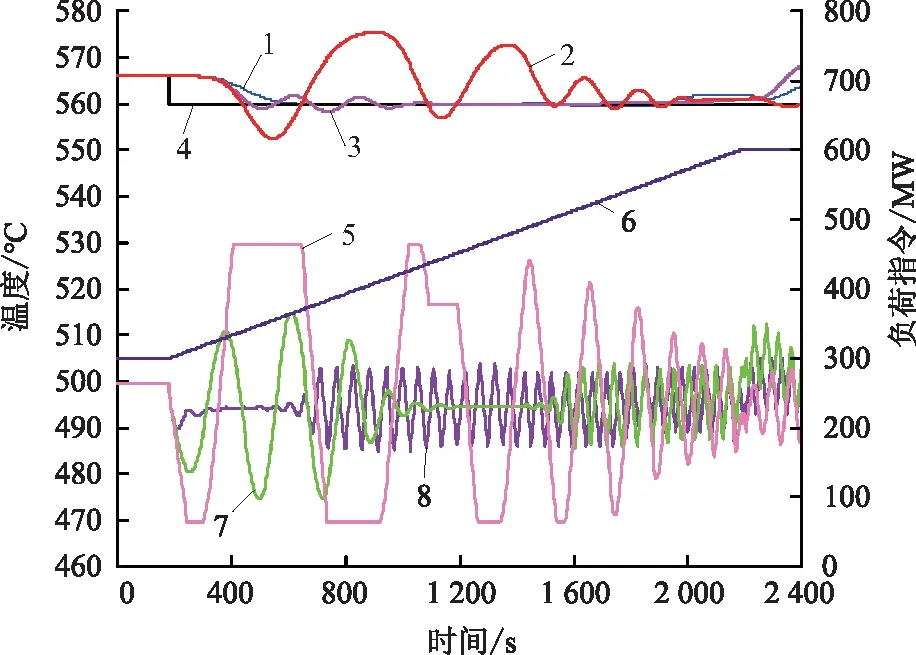
1—固定模型参数2过热汽温调节趋势；2—固定模型参数4过热汽温调节趋势；3—固定模型参数3过热汽温调节趋势；4—过热汽温设定值；5—固定模型参数4主回路控制输出；6—负荷指令；7—固定模型参数2主回路控制输出；8—固定模型参数3主回路控制输出。图11 固定模型参数GPC-PI控制器变负荷调节曲线Fig.11 Variable load regulation curves of GPC-PI controller with fixed model parameters

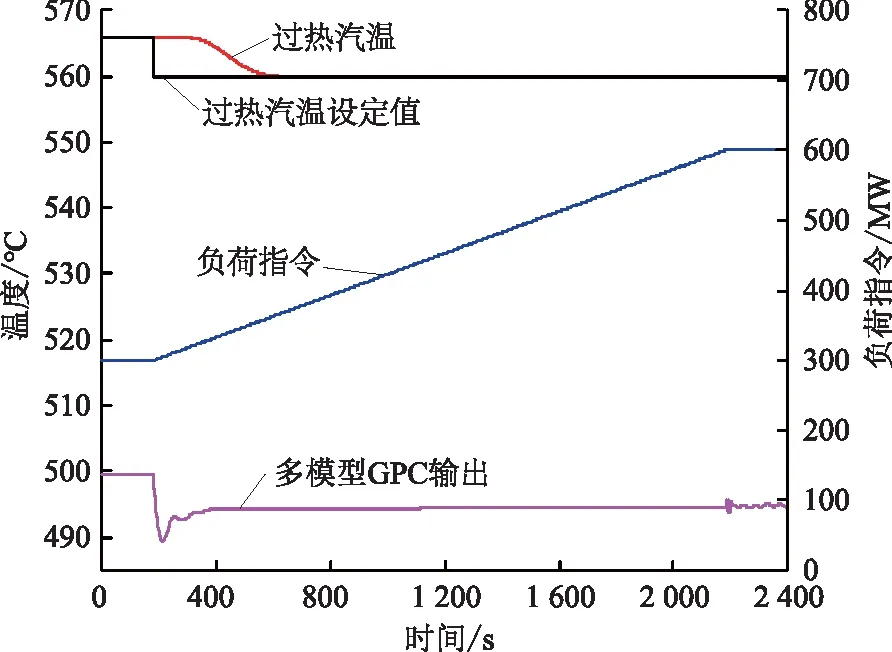
图12 多模型加权调度GPC-PI控制器变负荷调节曲线Fig.12 Variable load regulation curves of multiple model weighted scheduling GPC-PI controller

从图11、12中可以看出：当机组负荷接近模型参数对应的负荷段时，基于固定模型参数设计的GPC-PI控制器能够有效控制住过热汽温，当机组负荷偏离模型对应的负荷段时，调节效果开始变差，且控制器输出已出现振荡现象，无法满足实际控制要求；而多模型加权调度GPC-PI控制器在变负荷过程中表现良好，过热汽温在5 min左右便进入稳态控制偏差±3 ℃范围内，且一直维持在设定值附近，GPC控制器输出未出现明显跳变。

可见多模型加权调度的GPC-PI控制器，可以很好地解决单一模型GPC-PI控制器在变负荷时出现控制不佳的情况。

3.4 抗干扰性能测试

为测试系统克服被控量扰动的能力，依靠上节所构建37%Pn—100%Pn全过程喷水量扰动时的过热汽温动态特性，负荷指令以1.5%Pn/min的速率从50%Pn升至100%Pn，在800 s时于被控量处施加5 ℃的阶跃扰动，调节趋势如图13所示。

图13 多模型加权调度GPC-PI控制器抗干扰调节曲线Fig.13 Anti-interference adjustment curves of multiple model weighted scheduling GPC-PI controller

从图13中可以看出在施加阶跃扰动后，过热汽温平稳地重新回到设定值附近，说明多模型加权调度GPC-PI控制器具有良好的抗干扰性能。

4 结束语

通过单一工况下考虑减温水调节阀特性的预测控制仿真试验，验证了GPC-PI控制对减温水调节阀特性的变增益具有一定的鲁棒性，GPC控制器输出能够快速、稳定地控制过热汽温，相较常规串级PID控制器拥有更好的调节性能。基于固定模型参数的GPC-PI控制器在变负荷时无法达到良好的控制效果，容易引起系统振荡。基于多模型加权调度的GPC-PI控制器可以解决变负荷时模型失配带来的问题，增强了GPC的鲁棒性。抗干扰测试结果证明，多模型加权调度GPC-PI控制器具有良好的抗干扰性能。