洞庭湖区软基上的水闸动力响应分析

柳厚祥，胡楚鑫

（长沙理工大学 土木工程学院，湖南 长沙 410114）

洞庭湖区软基分布广泛且压缩性较高，建于软基上的老旧水闸数量众多。目前，除了险加固工程［1］，往往只重视水闸本身的结构强度，对水闸下软弱基础的重视程度不够，容易引发水闸不均匀沉降、翼墙倾斜失稳等安全隐患，甚至可能危及整个水闸的运行安全。洞庭湖区处于断裂带附近，曾多次发生地震，为避免水闸存在安全隐患，需要探究洞庭湖区水闸与软基的相互作用机理，并开展相应的动力响应分析。

目前，国内外的一些学者已经对软基上水闸进行了深入研究。殷晓曦等［2］对井字梁底板式水闸进行了有限元计算，得到了不同工况下各构件的内力和位移。彭渊等［3］采用ABAQUS软件研究了闸侧空箱对翼墙及桩基础位移的影响。廖文来等［4］利用监控手段探究了闸墩结构各指标的工作性态。王阳［5］通过改变结构及地基土的参数，分别对比在不同情况下闸室结构的受力特性。吴维军等［6］分析了加载对输水闸进水井沉降的影响，并提出了对应的地基处理措施。薛静静［7］比较了两种计算方法下双铰式闸室结构应力应变赋值结果。这些研究是基于静荷载下软基水闸的结果，并未涉及动力响应分析。陈凸立等［8］基于ANSYS 软件研究了闸坝的动力特性及稳定性。朱庆华等［9］采用振型分解反应谱法对闸室结构进行了计算，并提出了有针对性的抗震措施。崔春义等［10］采用振型分解反应谱和动力时程分析，验证了船闸的抗震性能。李火坤等［11-12］提出了软基水闸有限元模型参数修正方法和底板脱空动力学反演方法，以反映水闸结构真实的动力学特性。张建伟等［13］采用AVMD-KELM方法预测了水闸结构的振动趋势。这些研究大多以地震作用下水闸结构为研究对象进行受力变形分析，但未涉及水闸的软基稳定性。由于软基承载力普遍较低，在地震荷载下易导致水闸发生不均匀沉降甚至开裂等现象。

综上所述，考虑到在水闸结构和软基相互作用下的动力响应分析较少，现有规范也未提及相应的理论分析方法，且土体中的孔隙水压力、有效应力和沉降变形等均难以简单地通过理论方法进行简化计算。因此，在对洞庭湖区域分布的大中型水闸做了初步了解和筛选的基础上，本研究拟选用苏家吉排水闸作为洞庭湖软基上水闸的典型工程案例，采用FLAC3D有限差分软件建立三维数值动力仿真模型［14］，分析动力响应中水闸结构与地基土相互作用下的受力变形情况，以期为水闸抗震加固设计和施工提供参考。

1 工程概况

1.1 洞庭湖区软基特性

洞庭湖区位于长江中游南岸，跨湖南省和湖北省，行政区划包括湖北省4 个县市区及湖南省21 个县市区。由于洞庭湖区水系较为复杂，沉积环境多样，因此该地区的岩土结构表现出较大的复杂性。根据洞庭湖区堤垸地基的地质勘测报告可知，该地区地层上部主要为厚薄不一的淤泥土，具有高压缩性、低强度等特点，因此易产生较大的沉降及不均匀沉降［15-16］。

1.2 洞庭湖区水闸结构特性

洞庭湖区占地面广，天然湖泊容积也大。为了防止潮水倒灌以及在汛期排放洪水，在洞庭湖各堤垸处建立了大量具有挡水、泄水作用的水闸。根据最新统计数据，湖区大中型水闸共计122 处298 孔。按照闸身材质，可以分为钢筋混凝土、混凝土、浆砌石等。其中，钢筋混凝土材质占比65.57%，混凝土材质占比9.02%，其他材质占比25.41%。按照水闸类型，可以分为排水闸、撇洪闸、低排闸、节制闸等。其中，排水闸占比54.92%， 撇洪闸占比7.38%，低排闸占比6.56%，其他类型占比31.14%。

1.3 典型水闸结构形式

洞庭湖区的水闸典型结构形式以钢筋混凝土材质为主，其中，排水闸占主导地位。

以苏家吉排水闸作为典型水闸的案例进行分析。苏家吉排水闸位于沅水尾闾的软基上，采用混凝土平底板胸墙式整体结构，宽度为21.00 m，总净长为 70.28 m，共有5 个孔，单孔长为10.00 m。闸室底槛高程为26.50 m，底板厚度为1.50 m，内、外导水墙底槛高程为27.00 m，底板厚度为1.00 m，两岸堤防填土的高程一致。内、外导水墙基础布设钢筋混凝土灌注桩，桩长10.00 m。根据历年来最高水位情况，设计外河水位高程为40.00 m，内河水位高程为34.50 m。苏家吉排水闸平面和剖面如图1～2所示。

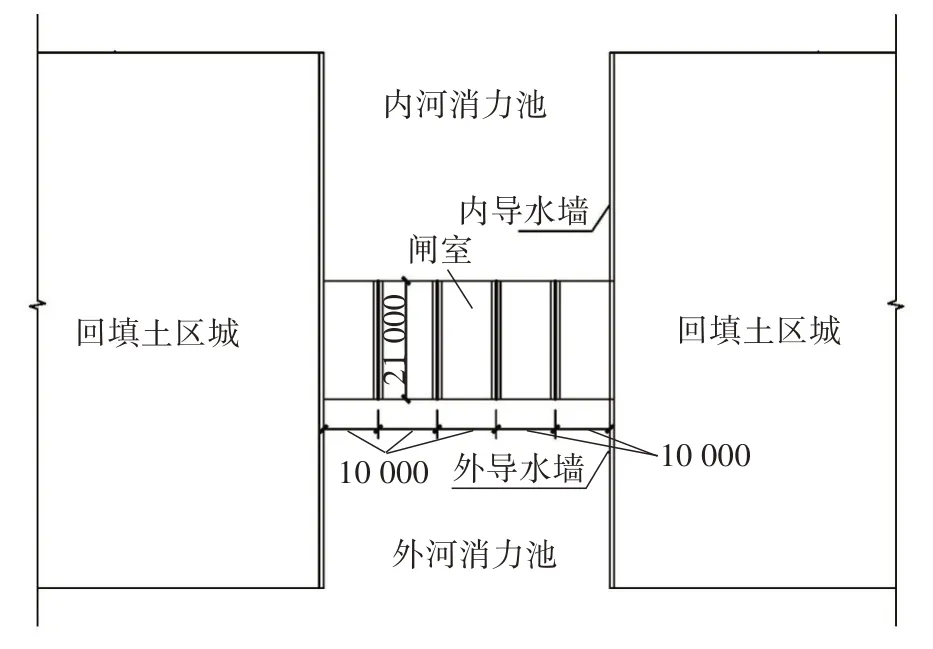
图1 苏家吉排水闸平面图（单位： mm）Fig. 1 Layout of Sujiaji Drainage Sluice （unit： mm）

图2 苏家吉排水闸闸室剖面图（单位： mm）Fig. 2 Section of Sujiaji drainage gate chamber （unit： mm）

1.4 典型水闸软基分布

根据苏家吉水闸的地质情况，如图3 所示。除人工填土区域外，其他主要为Q4al+1地层。

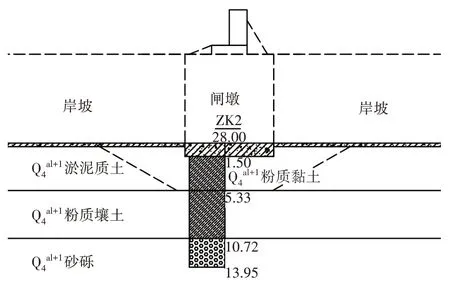
图3 苏家吉排水闸工程地质分布（单位： m）Fig. 3 Geological distribution of Sujiaji drainage gate project（unit： m）

从图3 中可以看出，在水闸轴线上的地基土为粉质黏土，土层厚度约3.80 m，处于可塑状态，属于相对良好的地基持力层。在约5.00 m 深度范围内，地基土为淤泥质土，具有高含水量、低强度、高压缩性的软土特征，容许承载力仅为60～70 kPa。在5.33 m至10.72 m深度范围内，地基土为冲湖积灰色粉质壤土，较密实，粉粒含量高，呈可塑状，承载力为140 kPa。在大于10.72 m 深度的为砂砾层，地基承载力较高，可以作为持力层。

2 三维数值模型的构建

2.1 模型建立

以苏家吉排水闸的水文地质、水闸结构设计及水位等条件为依据，利用FLAC3D软件构建了三维有限差分法数值仿真模型。模型在顺河流方向上的长度为121.00 m，垂直水流方向上的宽度为182.00 m，砂砾层的厚度设为5 倍桩长（即50.00 m）［17-18］。考虑到FLAC3D专门开发了外接接口，能够很好地兼容其他软件生成的网格文件，且ABAQUS 有限元软件的前处理具有便捷、强大等诸多优点，并能生成规则的单元体模型，适用于建立大型且复杂的三维模型，符合FLAC3D对单元体的要求，因此保证了其在计算过程中的精度。此外，尽管导墙和导墙下桩基础的作用是维持填土的稳定性，但导墙结构设计复杂，桩基础分布较广、数量繁多。为便于观察软基在水压力及地震荷载共同作用下的变化规律，将导墙及其桩基础简化成直墙形式。网格划分时，选用六面体单元来代表土体及水闸结构，模型网格划分的单元总数为41 096 个，节点总数为45 696 个。其中，土体单元总数为40 425个，ABAQUS有限元网格模型如图4所示。

图4 苏家吉排水闸三维有限元网格模型（单位： m）Fig. 4 3D finite element mesh model of Sujiaji drainage gate（unit： m）

选用直角坐标系来建立模型，以砂砾层底面左下角为原点，x轴为垂直水流方向，y轴为顺水流向下方向，z轴竖直向上。模型底部为固定边界，顶部为自由面，其他面则限制法向位移。为了合理地模拟水闸模型的受力状态，并考虑实际求解中的非线性问题，水闸闸室、导墙和砂砾层采用各向同性弹性本构模型（Elastic），模型中其他土体则采用弹塑性本构模型。假设土层是各向同性的材料，土体符合用莫尔-库仑（M-C）准则。在水闸闸室、导墙在土体相连接的位置上布置接触面，接触面参数的取值参考文献［19］。

2.2 材料参数

根据苏家吉排水闸勘查报告，将工程地质土体划分5种类型，水闸闸室、导墙结构混凝土材料选用C25强度等级，土体及结构材料力学参数见表1。

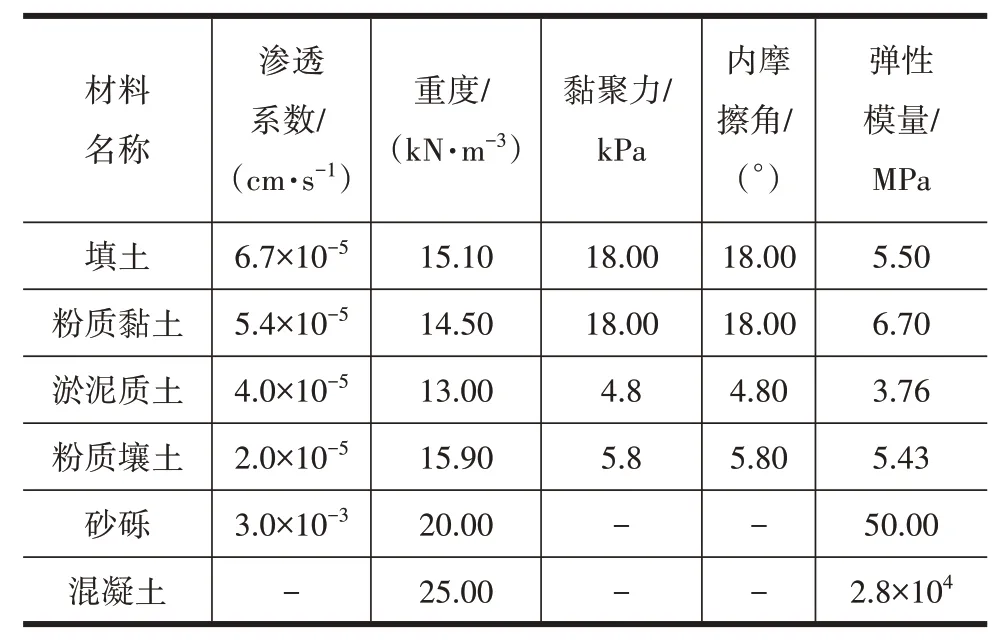
表1 数值计算力学参数Table 1 Mechanical parameters of numerical calculation

2.3 数值模拟工况

由于水闸内、外河两侧的设计水位不同，为更好观察软基在动力响应下的变化规律，将外河设计水位作为整体模型的水位线。同时，为了便于观察模型内部的响应情况，在闸室底部设置监测点，以观察孔隙水压力、有效应力、竖向沉降等各项指标。监测点位置如图5所示，具体数据见表2。

表2 监测点分布Table 2 Monitoring point distributions

图5 苏家吉排水闸闸室下监测点Fig. 5 Setting of monitoring points under the gate chamber of Sujiaji drainage gate

针对水闸动力的研究，主要有拟静力法、反应谱法和时程分析法等方法［20］，但拟静力法和反应谱法无法完整体现出建筑物在真实地震波作用下的全过程响应，因此无法准确反映结构的真实受力情况［21］。为了模拟地震对苏家吉排水闸的影响，考虑到苏家吉排水闸三维数值模型的复杂性，以及水平顺河向地震能对水闸闸墩产生的线性增长的惯性力，对结构的稳定性的要求更高［21-24］。

本研究采用地震波沿水平顺河向进行震动，地震波的波峰值为0.1g。由于该地震波每次往返作用的周期值分布在0.1～0.5 s，地震作用频率约为2～10 Hz。因此，在动力计算之前，须在SeismoSignal软件中对地震波进行滤波和基线校正。其步骤如下：

1）先对地震波中频率大于10 Hz 的部分进行过滤。

2）通过添加多项式的方式，使得地震波的累计速度和累计位移近似为零。

3）对比地震波基线校正前后的数据，可以发现校正前的累计位移高达15.00 cm，而校正后的累积位移小于0.20 cm，同时累积速度非常小。

地震波基线校正后的数据如图6所示。

图6 地震波基线校正后数据Fig. 6 Corrected dates of seismic wave baseline

3 软基上水闸的静力分析

为了真实地进行水闸模型的仿真计算，须在动力计算之前对该模型进行静力分析，以获取初始应力场的分布结果。水闸在承受自重、土压力、水压力等荷载作用下产生一定沉降。采用FLAC3D有限元软件计算初始地应力的步骤如下：

1） 先对材料赋予干密度，采用弹塑性计算方法，计算初始应力。

2） 开启渗流模块，将混凝土材料设置为不透水模型，将土体单元设置为各向同性渗流模型。

3） 在整个模型上施加相应的水位，并对内、外河消力池及导墙施加静水压力。

在未考虑水压力的影响下，模型竖向变形云图如图7所示。

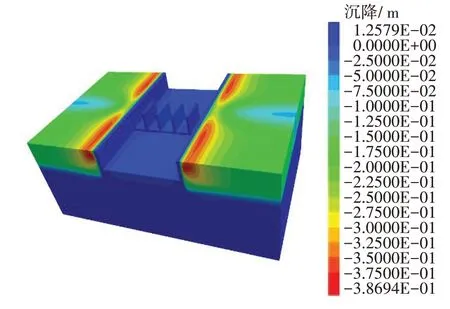
图7 竖向变形云图（单位：m）Fig. 7 Vertical deformation cloud calculated （unit： m）

从图7中可以看出，淤泥质土层上的水闸两侧填土在导墙处有明显竖向沉降，最大沉降量为0.38 mm，这是由于导墙与土体刚度有差异所导致的。相比之下，粉质黏土层的强度大于淤泥质土层的，因此粉质黏土层上的填土的最大竖向沉降仅为0.26 mm，约占为68%。值得注意的是，所有导墙底部在计算结束后均出现了局部隆起现象，这是因为导墙两侧存在较大的高度差，加上淤泥质土层的抗剪强度低，容易使得填土的推力在重力作用下绕过导墙，作用于消力池处的土体上。同时，也可以观察到隆起现象随着远离导墙而出现迅速减弱的趋势，使得消力池中部区域的竖向沉降大于隆起值，从而表现为沉降。

在考虑水压力的影响下，模型施加水压力后的竖向变形云图如图8所示。

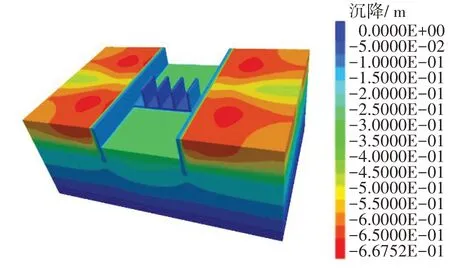
图8 施加水压力后的竖向沉降云图 （单位：m）Fig. 8 Vertical settlement clouds after applying water pressure （unit： m）

从图8中可以看出，在设置水位线后，水闸淤泥质土层上的填土在原有基础上进一步发生竖向沉降，增长了约72%。这是因为水分子进入孔隙后可以有效地降低土体抗剪强度，加上孔隙水在重力作用下产生的静水压力荷载，使得淤泥质土层和填土层得到了进一步挤压。填土在静水压力作用下加剧了向消力池方向移动的趋势，使得最大沉降的范围仅集中在导墙附近，最大沉降为0.67 m，但消力池内部同样受到静水压力荷载，这抑制了导墙底部的隆起。值得注意的是，粉质黏土层上的填土在闸室处也开始出现小范围的竖向沉降，这可能是由于周围土体发生不均匀沉降时，填土层土颗粒间的黏聚力发挥出一定的作用，快速沉降的土颗粒会对沉降较慢的土颗粒产生牵引力，而这种牵引力主要集中于填土层内侧。因此，填土分的竖向沉降表现出从内至外递减的现象。

4 软基上水闸的动力响应分析

在静力计算结果基础上，采用FLAC3D软件的动力模块和渗流模块进行软基上水闸的动力计算。为吸收地震波在边界上的反射，在动力计算时，对模型四周设置自由场边界，以达到模拟无限场地的效果。动力响应分析主要是分析水闸竖向变形以及监测点各指标的时程变化。

4.1 监测点加速度响应分析

为方便比较监测点A1和A2在施加地震荷载后的加速度响应值，定义了监测点加速度时程上的峰值加速度与输入地震波加速度时程上的峰值加速度的比值为PGA 放大系数。根据图9 的数据，可以得到监测点A1和A2的PGA 放大系数分别为1.55 和1.23，并发现砂砾层的厚度和强度远大于粉质壤土层和粉质黏土层的。当地震波从底部传递到粉质壤土层时，监测到的PGA放大系数增加了23%，而从粉质壤土层传递到粉质黏土层时，监测到的PGA 放大系数增加了约26%，这反映出在地震作用下，低强度土体的PGA 放大系数的增幅比高强度土体的变化更快。同时，通过与图6中地震波基线校正后的数据比较，可以发现监测点的峰值加速度在时间点上滞后于输入地震波的峰值加速度。这表明地震的传播是从震源处逐步扩散的，且不同高程位置接收到的地震波时间存在差异。

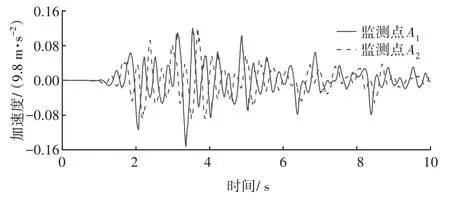
图9 闸室监测点加速度时程Fig. 9 Acceleration timescale of gate chamber monitoring points

4.2 竖向沉降变化分析

动力计算结束后的竖向沉降如图10 所示。从图10 可以看出，在动力计算结束后，填土区域存在不同程度的隆起现象。其中，粉质黏土层以上的填土区域的隆起现象最为突出，高达30.5 mm。这是因为在水平顺河向地震波作用下，淤泥质土层较粉质黏土层更容易使得上方的填土区域产生滑动。这导致粉质黏土层上的填土不断承受两侧填土的挤压。当加速度时程进入主震阶段后，两侧的挤压作用变得更加强烈；而当接近地震尾声时，挤压作用逐渐减小，但并未完全消失。因此，动力计算结束后，粉质黏土层上的填土维持在较高的隆起状态，而其他范围填土的隆起值则普遍较低。

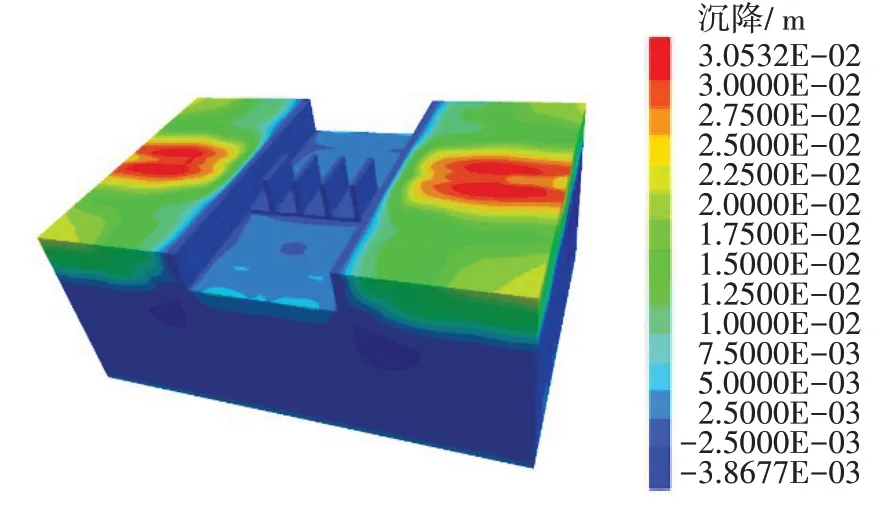
图10 动力计算结束后的竖向沉降云图（单位：m）Fig. 10 Vertical settlement cloud at the end of the dynamical calculation （unit： m）

监测点的竖向沉降时程曲线如图11 所示。从图11 可以看出，曲线一开始急剧上升，但在主震阶段出现跳跃式变化。随着地震波幅值的减小，曲线跳跃动作消失，同时增长速率逐渐变缓，最终在地震临近结束时维持在一个稳定的状态下。考虑到在上部闸室自重荷载约束下，监测点A1的竖向沉降略大于监测点A2的。这表明在竖向变形方面，淤泥质土的存在会影响到闸室下地基的稳定性。尤其是在对应的输入地震波峰值加速度时间点附近，两个监测点的竖向沉降值的差异最大达到0.34 mm。

图11 闸室监测点竖向沉降时程Fig. 11 Time course of vertical settlement of gate chamber monitoring points

4.3 监测点超孔压与有效应力增量分析

闸室监测点的超孔隙水压力和有效应力随时间的变化如图12～13 所示。从图12～13 可以看出，超孔隙水压力和有效应力增量随着时间的推移整体呈增加趋势。其中，监测点A1在前1.0 s 内的变化趋势最为明显，呈现出倒Z 字形。从图5 和图10可以看出，在前1.0 s 内，由于地震幅值普遍较低，监测点土层的孔隙水压力得到一定程度的消散，有效应力也有所增长。然而，随着地震幅值的逐渐增大，超孔隙水压力和有效应力的增长速率迅速上升。在3.5 s 之后，两者的增长速率逐渐变缓，监测点A2甚至开始出现孔隙水压力消散的现象。这可能是由于来自低高程位置的高孔隙水压力和高有效应力，以及在砂砾层共同影响下的结果。

图12 闸室监测点超孔隙水压力时程Fig. 12 Time course of excess pore water pressure of gate chamber monitoring points

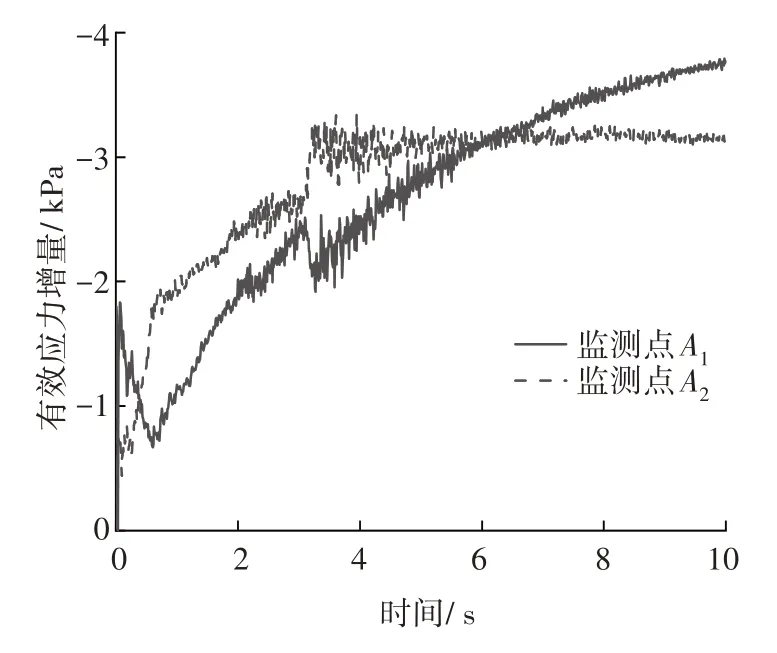
图13 闸室监测点有效应力增量时程Fig. 13 Time scale for increasing effective stress of gate chamber monitoring points

5 结论

本研究基于软基上苏家吉排水闸的三维动力数值计算结果，分析了水闸两个计算阶段的竖向沉降、监测点的加速度响应规律，以及竖向沉降、孔隙水压力和有效应力的发展趋势。得出以下结论：

1） 在施加水压力作用前，填土区域有向消力池内部移动的趋势，导致导墙底部产生部分隆起。施加水压力作用后，靠近导墙内部填土范围的沉降加剧，而导墙底部在静水压力作用下隆起现象得到进一步约束。

2） 在地震传播过程中，砂砾层的厚度和强度高于粉质壤土层和淤泥质土层的，但其PGA 放大系数增长缓慢。不同高程监测点的加速度具有时间滞后现象。

3） 在地震作用时，由于淤泥质土层自身抗剪强度较低，该土层上部的填土在地震发生的全过程中不断对粉质黏土层上部的填土进行挤压，使得该区域出现了较大范围的隆起现象。

4） 随着地震的不断作用，孔隙水压力、有效应力和加速度幅值呈现规律性变化。在地震荷载施加的前期阶段，加速度幅值普遍较低，孔隙水压力和有效应力表现为先升后降。当地震迎来峰值加速度后，孔隙水压力和有效应力增长速率达到最大值。在地震临近结束时，孔隙水压力和有效应力增长较为缓慢，邻近砂砾层的粉质壤土层甚至开始出现孔隙水压力消散和有效应力增加的现象。