放坡状态有限土体刚性挡墙滑动稳定性分析

刘新喜，贺程，王玮玮，李彬

（长沙理工大学 土木工程学院，湖南 长沙 410114）

近年来，随着基础设施建设的不断发展，高路堤挡墙和相邻基坑中的挡土结构后方出现了放坡状态下的有限宽度土体。对于这种类型的工程设计来说，计算挡墙的稳定性是关键。关于挡墙滑动稳定性的研究，大部分学者先计算挡墙的滑动驱动力和抗滑力，然后计算挡墙稳定性。然而，这个计算过程相当复杂，且针对在放坡条件下对有限土体刚性挡土墙稳定性的计算研究鲜见。因此，对这类工程的挡墙稳定性进行深入研究是十分必要的。

目前，国内外有许多学者对半无限土体的挡土墙稳定性进行了研究。HANDY［1］研究了两个平行挡土墙，发现墙背粗糙竖直，并推导出了挡墙后土压力分布的计算公式。FRYDMAN 等［2-3］在邻近基岩面处，研究了以砂砾土为填土的刚性挡土墙在主动土压力和静止土压力状态下的侧向土压力。应宏伟等［4］假定墙后填土产生了圆弧形土拱，通过计算推导出考虑了墙土摩擦角的主动土压力。卢坤林等［5］在挡土墙平动模式下，考虑了土拱效应与挡土墙位移的影响，建立了非极限主动土压力的计算公式。徐日庆等［6］考虑了墙土摩擦角和黏聚力的影响，得到了黏性土非极限主动土压力的计算公式。刘杰［7］研究了挡墙稳定性，在半无限土体的假设下，引入极限分析上限法理论，将挡墙与土体视作一个整体进行分析，通过求解矢量三角形，计算出外力做功功率以及能量耗散功率，建立了能量平衡方程，采用能量估算法在不求解土压力的情况下，使用MATLAB软件，得出挡墙稳定性系数的数值解，并分析了各参数对相应稳定性系数和破裂角的敏感性。刘洋等［8］考虑了土条上下界面之间切应力的影响，推导出了挡土墙上的主动土压力的理论计算式。石位哲［9］以砂土作为试验对象，通过平移模式试验，发现墙后填土最终会形成一个贯穿土体的滑裂面，土体的塑性区会形成一条从墙角到填土表面的塑性带。方鹏等［10］基于极限平衡理论，将圆弧形挡土墙视为整体，得到了土压力的计算方法。

对于有限土体刚性挡墙稳定性的研究，已经取得了丰硕的成果。应宏伟等［11］以无黏性填土为研究对象，通过数值模拟方法，推导出了土压力分布公式和合力作用点的理论计算式。杨明辉等［12］开展了无黏性土在刚性挡墙平动等位移模式下的主动土压力试验，分析了土体变形和土压力分布规律。王闫超等［13］考虑了无黏性土的有限土压力问题，运用薄层单元法，推导出极限破裂角及土压力的表达式。杨明辉等［14-16］在考虑土拱效应的条件下，对有限土体土压力进行了研究。方焘等［17］通过模型箱进行了在浸水条件下有限宽度无黏性土体的主动土压力试验，得出了不同宽度下的土体破坏模式和土压力分布规律。刘忠玉［18］针对墙后为有限无黏性填土的刚性挡土墙，修正了水平层分析法，得出在平动模式下刚性挡土墙主动土压力的表达式。

虽然学者们已经将挡墙稳定性的研究推广到了有限土体，但是针对放坡状态下的土体研究较少。方焘等［19］使用极限平衡法，推导了在放坡条件下有限土体主动和被动土压力的计算公式，但忽略了墙背填土黏聚力。胡卫东等［20］引用刚体平衡理论，研究了相邻基坑、路堤与切坡挡土墙形成放坡状态下的有限土体，考虑了滑裂面通过斜坡面和坡顶面的两种情况，建立了放坡状态下的主动土压力计算模型，分析了各参数对极限破裂角和主动土压力的影响，并通过模型试验验证了公式的合理性。这些学者的研究对象为有限土体，当分析挡墙稳定性时都需要计算土压力，求解过程比较复杂。

综上所述，目前关于放坡状态下有限土体刚性挡土墙的稳定性研究存在计算过程烦琐和参数考虑不全等问题，有待进一步地探讨与研究。因此，本研究以挡墙与墙后填土的整体为研究对象，基于极限分析上限法，得出放坡状态下有限土体刚性挡墙稳定性的简化计算方法，省略计算挡墙土压力的过程。同时，分析了墙后土体的宽高比、黏聚力、内摩擦角、墙土界面摩擦角和墙土界面黏聚力等参数对挡墙稳定性的影响，以期为此类工程设计提供参考。

1 放坡状态挡墙稳定性计算

1.1 挡墙的平移滑动理论模型

在挡墙平移滑动破坏模式中，其计算模型示意如图1所示。

图1 挡墙稳定性理论模型Fig. 1 Theoretical model of retaining wall stability

基本假定如下：

1） 墙后填土为均质黏土；

2） 挡墙在土压力的作用下，没有发生转动，但产生了远离填土的平移运动。

在图1 中，假设：墙背竖直，墙后放坡状填土为黏性土体，填土表面水平；刚性挡土墙高度为H；临界深度为h；墙后顶面有限宽度为l；重度为γ；挡土墙底面为速度间断面；δa为挡土墙底面摩擦角；Va为挡墙运动速度；Vb为填土与挡土墙的相对运动速度；δ为挡土墙与填土的界面摩擦角；Vc为填土区运动速度；φ为土体内摩擦角；斜坡底角为β；破裂角为α。

根据图1 所示的几何关系，可以求出各边的长度：

根据极限分析上限法，Va、Vb、Vc3个矢量必须满足速度相容关系，如图2所示，其表达式为

图2 速度矢量关系Fig. 2 Relationship between velocity vectors

根据式（1）与图2的几何关系，以及三角形正弦定理，可得

1.2 做功功率与能量耗散

应用极限分析上限法，结合图1，研究墙后四边形ABEO区域的填土，计算外力做功功率及能量耗散功率。

1） 均布荷载P的做功功率Wp。

均布荷载P在ABEO区域上做功，长度为-----AB。P沿竖直方向向下，与Vc方向成90° +φ-α的夹角。其表达式为

2）ABEO区域填土重力做功的功率Wg。

重力方向为竖直向下，且与Vc方向夹角为90° +φ-α。其表达式为

式中：γ为填土重度。

3） 沿AO界面的能量耗散DAO。

四边形ABEO的AO为墙土界面，AO界面的总黏聚力，记为Cw，如图1所示，其表达式为

式中：cw为墙土界面黏聚力。

Cw与Vb的夹角为δ，则能量耗散DAO可以表示为

4） 沿EO界面的能量耗散DEO。

四边形ABEO的EO为填土的滑裂面，EO界面的总黏聚力记为C，如图1所示，其表达式为

式中：c为填土黏聚力。

C与Vc方向成φ夹角，则能量耗散DEO可以表示为

5） 沿挡墙底面FO的能量耗散DFO。

FO边为墙土界面，FO界面的总黏聚力记为CL，如图1所示，其表达式为

式中：cL为墙土界面黏聚力。

CL与Va的夹角为δa，则能量耗散DFO可以表示为

6） 挡土墙的重力做功功率Wwg。

挡土墙重力方向竖直向下，与Va的夹角为90o-δa。其表达式

式中：Ww为挡土墙重力。

7） 建立能量平衡控制方程。

基于极限分析上限法，ABEO区域填土的所有外力做功功率与能量耗散之和为零：

即：

式（14）中，共含6 项，外力做功功率为前三项，内能耗散功率为后三项，且每项都含有一个参数Vc，而Vc为填土区ABEO的运动速度，将参数Vc消除，即：

1.3 挡墙稳定性系数

应用能量法估算稳定性系数Fs的表达式为

式中：

∑D表示总能量耗散功率；

∑Wnegitive表示外力做功为负功的总功率；

∑Wpositive表示外力做功为正功的总功率。

当外力做负功时，该力利于墙土系统稳定性，因此，∑Wnegitive只包含挡墙的重力做功功率。当外力做正功时，该力不利于墙土系统稳定性，因此∑Wpositive只包含塑性区ABEO区域填土的Wg与P的做功功率。

将式（18）～（20）带入式（17），则有

式中：

当式（21）满足条件

此时，对应的α为破裂角，计算得到挡墙的稳定性系数Fs最小值。当Fs= 1 时，墙土系统处于能量平衡的极限状态。

2 公式验证

为验证该方法合理性，采用建筑边坡工程技术规范［20］计算文献［21］算例的稳定性系数，并与该方法的结果进行对比，同时与库伦主动土压力计算的挡墙稳定性结果进行对比。设挡墙顶面宽度为0.5 m，底面宽度为4.0 m，挡墙高度为10 .0 m，坡底角为40°，挡墙重度为25.0 kN/m3。结果见表1。

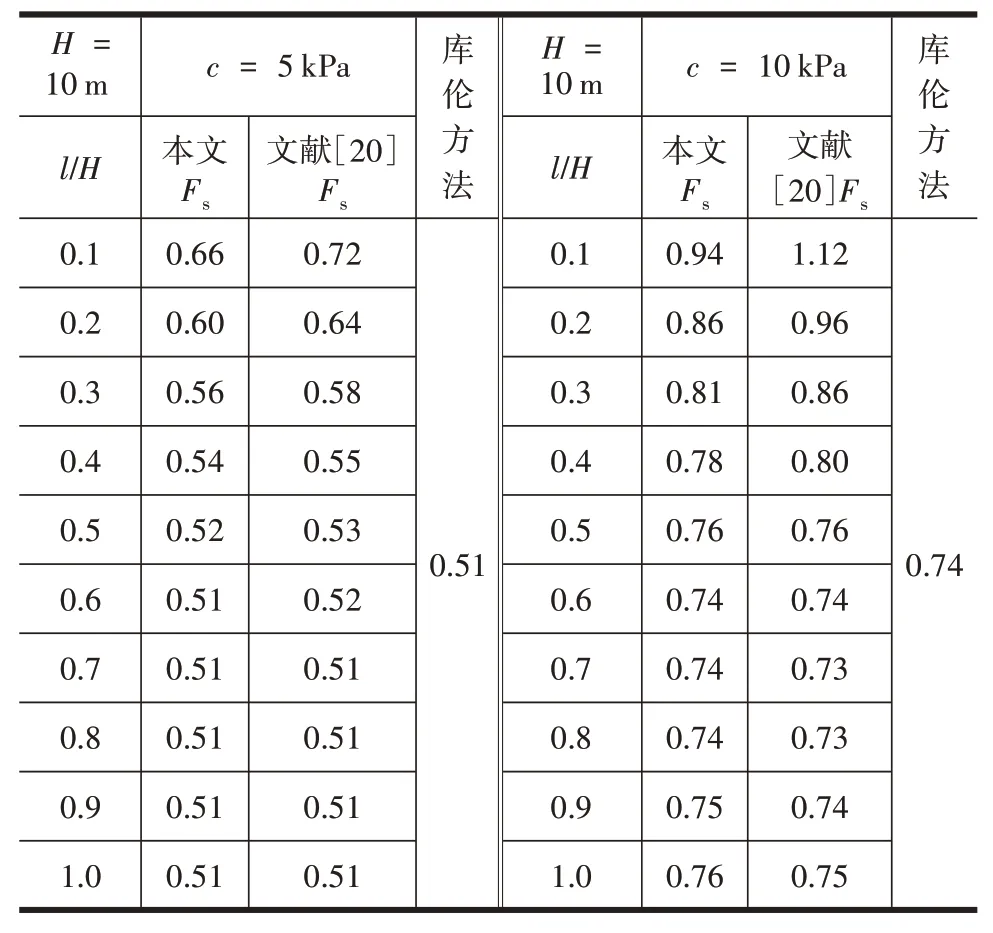
表1 Fs计算对比值Table 1 Calculate the logarithm ratio of Fs

由表1可知，稳定性系数Fs随着l H的增大而减小，并随着宽度l的增加，逐渐接近半无限土体库伦方法所得到的稳定性系数。与文献［20］相比，该方法Fs的变化规律基本一致，但简化了计算过程。

3 参数敏感性分析

为了分析各类参数对挡墙稳定性的影响，以放坡状态下的黏性土体为例，假设墙背竖直，挡墙重度γw= 25.0 kΝ/m3，挡墙高度H= 10.0 m，挡墙底面长度La= 4.0 m，挡墙顶面宽度为0.5 m，填土顶宽l= 8.0 m，填土重度γ= 19.6 kΝ/m3，填土内摩擦角φ= 20°，墙背面摩擦角，墙底面摩擦角，填土黏聚力c= 20 kPa，墙土界面黏聚力［22-25］，墙底面黏聚力坡底角β= 40°，均布荷载P=0。

3.1 不同黏聚力下l/H对稳定性系数Fs影响

在保持其他条件不变的情况下，改变填土黏聚力c和l/H的取值。不同c的情况下，Fs与l/H关系如图3 所示。从图3 可以看出，随着土的黏聚力的增大，稳定系数Fs显著增加；在相同黏聚力的情况下，稳定系数随宽高比l/H的增加呈先递减后稳定的趋势；不同黏聚力的变化趋势大致相同；当l/H的值大于0.6后，稳定系数Fs基本保持不变。

图3 不同黏聚力下Fs -（l/H）的关系Fig. 3 Relationship between Fs and l/H under different c

3.2 摩擦角δ及δa对稳定性系数Fs的影响

在保持其他条件不变的情况下，改变墙背面摩擦角δ或墙底面摩擦角δa的取值。δ、δa与Fs的关系如图4所示。

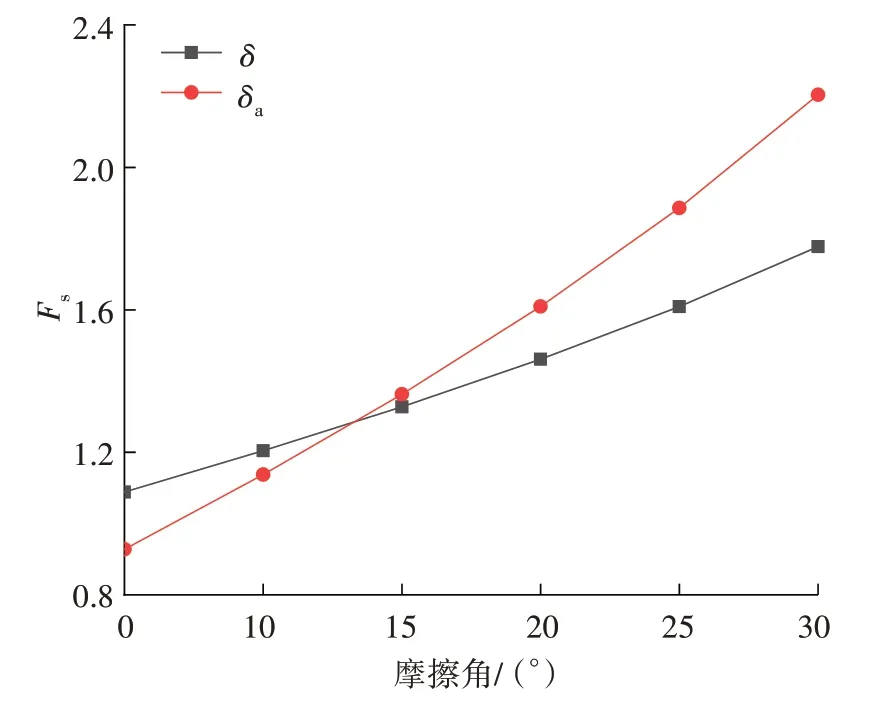
图4 Fs与δ、δa关系Fig. 4 Relationship between Fs and δ，Fs and δa

从图4 可以看出，稳定性系数Fs随墙背面摩擦角δ的增大而增大，且二者近似呈线性关系；当其他参数均不改变时，稳定性系数Fs随墙底面摩擦角δa增大而增大；δ的增长趋势小于δa的。

3.3 黏聚力cw及cl对稳定性系数Fs的影响

通过两种情况，得到cw、cl与Fs的关系。这两种情况的假设是：① 给定墙土界面黏聚力cw的取值，其余条件不变；② 给定墙底面黏聚力cl的取值，其余条件不变。其结果如图5 所示。从图5 可以看出，稳定性系数Fs随墙土界面黏聚力cw的增大而增大，且二者近似呈线性关系；挡墙稳定性系数Fs随墙底黏聚力cl的增大而增大，其曲线近似平行；cw的增加趋势大于cl的。

图5 cw、c1与Fs关系Fig. 5 Relationship between Fs and cw，Fs and cl

3.4 填土内摩擦角φ对稳定性系数Fs的影响

当改变填土内摩擦角φ的取值，其余条件不变时，Fs与φ的关系如图6所示。

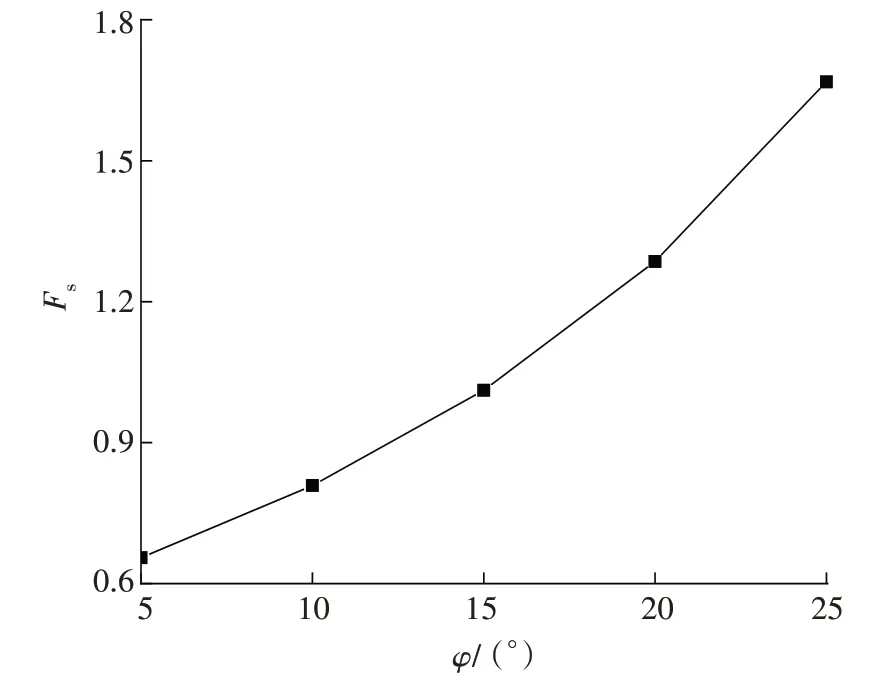
图6 Fs与φ的关系Fig. 6 Relationship between Fs and φ

从图6 可以看出，稳定性系数Fs随填土内摩擦角φ增大而增大，且随着φ的增大，稳定性系数Fs的增长速度越来越快。

4 结论

本研究对放坡状态下有限土体刚性挡墙的稳定性进行了分析，得出以下结论：

1） 本研究考虑了填土顶面荷载作用、墙土黏结作用、填土与挡墙墙背和墙底的摩擦作用以及土体黏聚力的影响，利用极限分析上限法，研究了挡墙在平移模式下的稳定性，省略了土压力的计算过程，建立了放坡状态下有限土体刚性挡墙稳定性的简化计算模型。

2） 通过使用本文提出的方法，当土体宽度趋近于半无限土体时，计算出的Fs与库伦方法的计算结果接近，验证了本文方法的合理性与正确性。

3） 挡墙稳定性系数随土体黏聚力、墙土界面摩擦角、墙土界面黏聚力及土的内摩擦角增大而增大；与宽高比呈反比关系，随宽高比的增加呈先递减后逐渐趋于稳定。