基于小波变换和FastICA的眼电伪迹去除研究

汪林恩, 耿晓中, 张 茜, 岳梦哲, 户唯新

(1.吉林化工学院信息与控制工程学院, 吉林 吉林 132022;2.长春工程学院计算机技术与工程学院, 吉林 长春 130012)

0 引言(Introduction)

脑机接口是目前较为前沿的人机交互模式。脑电信号的纯净程度决定了整个脑机接口系统的性能。在脑电信号的采集过程中会产生较多的伪迹信号,这些伪迹信号常由生理源引起,如人的眼睛、肢体和脑磁干扰等。其中,由眼球运动所引起的眼电伪迹是最显著且最常见的干扰信号,主要由低频率和高振幅的信号构成[1]。为了从脑电信号中获取更多有效且可靠的信息,研究将眼电伪迹从脑电信号中去除,并保留源信号的有效成分具有十分重要的意义。

针对当前脑电信号中眼电伪迹去除不彻底和有效成分提取不充分等问题,本文通过对当前脑电信号处理领域内的多种去噪算法进行研究,提出一种结合小波变换和FastICA的去噪方法。这两种算法从不同的角度处理信号,通过将原始信号进行小波变换去噪后再输入FastICA进行处理,可以去除不同类型的噪声和伪迹。FastICA基于独立成分分析,可以分离出信号中的不同成分;而小波变换则侧重于时频域分析,能够在不同尺度上捕捉信号的特征[2]。经实验对比表明,相较于单一算法,本文提出的融合算法对眼电伪迹具有更好的去除效果,为脑电信号处理提供了一种新的思路。

1 算法原理(Algorithm principle)

1.1 小波变换

小波变换(Wavelet Transform,WT)是一种基于多尺度分析的信号处理技术,用于分析信号或数据的频率成分和时域特征,在信号和图像处理等领域具有广泛的应用[3]。在小波变换处理过程中,通过选择不同类型的小波函数,可以获取信号中的不同特征,例如瞬时变化和周期性等。小波变换可以将信号分解为不同尺度下的信号成分,并根据噪声和信号间的尺度差异选择性地重新组合。脑电信号通常具有高频率和低幅值等特点,并且能量分布相对广泛,而眼电信号则呈现出低频率、时域有限以及能量集中等特征[4]。根据眼电信号的产生机理,以及小波分解中小波系数的意义,本文采用小波阈值法滤除脑电信号中眼电伪迹的干扰。

在小波信号处理领域,基于软阈值和硬阈值的小波消噪算法是应用较广泛的方法之一。设有如下检测信号:

y(k)=s(k)+n(k)

(1)

其中:s(k)为有效脑电信号,n(k)为高斯白噪声信号,满足n(k)～N(0,σ2),即服从均值为0、方差为σ2的正态分布。小波消噪的核心问题是如何从被干扰的信号y(k)中去除伪迹信号,从原始信号提取有效脑电成分s(k)。

小波变换法一般有以下几个步骤。

(1)选定适合的小波基函数u,利用与它对应的分解尺j分解原始脑电信号并进行离散小波变换,获取各个尺度上的小波系数Uj,k。

(2)选定适合的小波阈值λ,确定与其对应的阈值处理函数g(Uj,k)。

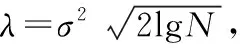
在脑电信号处理过程中,因为在不同尺度上信号和噪声的小波变换系数具有不同的传播特性,即随着分解尺度的变化,信号与噪声会呈现出不同的幅值和稠密度特征。因此,本文改进了传统固定阈值方法,引入自适应阈值策略可以更准确地适应信号特征。采用自适应阈值策略如下:

(2)

由公式(2)可以看出,随着分解尺度的增加,阈值λ也随之降低。这是由于小波变换系数在不同尺度下信号和噪声的传播特性不同,即随着分解尺度的提高,噪声的小波系数的模极大值逐渐减小,而脑电信号的模极大值逐渐增大。这种趋势正好对应了信号与噪声之间的幅值变化特性。

在小波变换中,常见的阈值处理方法包括硬阈值和软阈值,前者将小于阈值的系数置零,后者则对于大于阈值的系数进行缩放处理。在硬阈值处理中,其处理函数如下:

(3)

从公式(3)可以看出,小波系数Uj,k在λ和-λ是不连续的,这样会引起较大方差且不稳定。

在软阈值处理中,其处理函数如下:

(4)

在公式(4)中,小波系数虽然呈连续分布,但是各个小波系数之间存在一定的偏差,从而会影响伪迹的去除精度,因此参考公式(4)构造新的阈值处理函数:

(5)

其中:当N→0时,Uj,k为硬阈值处理函数;当N→∞时,Uj,k为软阈值处理函数。因此,当N取某一随机常数时,公式(5)则为介于硬阈值和软阈值的一个处理函数。

1.2 FastICA

独立成分分析(Independent Component Analysis,ICA)是一种用于分离多个混合信号成分的统计方法,广泛应用于信号处理和数据分析等领域[5]。原始的脑电信号可以被看作是由真实纯净的脑电信号和眼电信号等相互独立的信号源经过线性组合后产生的一组混合信号,当源信号和混合矩阵未知时,假设各源信号之间相互统计独立,ICA算法就能有效分离出混合信号中的期望分量[6]。基于最大负熵准则的FastICA算法适用于各种数据类型,以其高速收敛和分离效果好等优点在信号处理领域得到广泛应用。

FastICA基于独立性假设,通过最大化信号的非高斯性找到源信号;FastICA算法的主要步骤包括中心化信号、白化处理以消除相关性,然后使用迭代优化方法,逐步提取出独立成分,是进行ICA的一种快速算法[7]。FastICA不仅具有传统独立成分分析的优点,而且在传统ICA方法的基础上进一步改进,提升了算法的收敛速度和稳定性,能更精确地分离出源信号中的眼电信号分量[8]。

FastICA算法以最大化负熵为导向,通过优化过程逐个分离独立分量;随机变量的随机性强度和它的预测性难度密切相关,随机变量越难预测,则随机性越突出且这个随机变量的熵值越大。在一组单位方差的随机变量集合中,高斯变量具有最大熵值,说明随机变量的非高斯性可通过其熵值进行量化[9-10]。从微分熵的概念可以推导出一种度量,称为负熵。负熵可用以下公式计算:

Qg(L)=R(LGauss)-R(L)

(6)

其中:LGauss为高斯随机变量且与L具有相同的方差,R(·)为随机变量的微分熵。微分熵可由下述公式定义:

(7)

在一组单位方差的随机变量集合中,高斯分布变量具有最大熵值。L的非高斯性越强,那么它的微分熵就越小,Qg(L)的值就越大;当L服从高斯分布时,Qg(L)=0。由公式(7)可知,实际条件下无法通过已知L的概率密度分布函数计算微分熵,因此可以用近似公式代替:

Qg(L)=(H(g(L))-H(g(LGauss)))2

(8)

其中:H(·)为均值运算,g(·)为非线性函数,通过获得的Qg(L)极大值确定源信号是否达到最大程度的独立。

利用固定点算法,通过应用非线性单调函数和牛顿公式可以计算出负熵的估计值,其公式如下:

(9)

(10)

(11)

其中:W为分离矩阵,Z为正交白化矩阵。

FastICA算法主要分两个步骤:第一步对信号进行去均值、白化及归一化处理,确保信号具有零均值并消除相关性,同时减少待估计参数,用于简化后续的独立分量分析过程,降低计算复杂度。第二步通过迭代寻优提取出独立分量。

2 数据集描述(Dataset description)

本次实验采用的数据来源于BCI competition IV公共数据集Datasets 2a,该数据集由9名受试者的脑电图数据组成,设计的脑机接口范式包括四种不同的运动想象任务,即对左手、右手、双脚和舌头的运动想象任务。受试者在不进行肌肉运动的情况下仅通过想象手部运动产生脑信号,每个试次由一个时间段组成,屏幕提示内容为与部分运动类别相关的图标或文字,参与者会根据屏幕上的提示想象特定的动作。试次的排列是随机的,以保证数据的多样性和可靠性。数据包含22个脑电通道及3个单极脑电通道,采样频率为250 Hz。图1为脑电信号采集范式示意图。

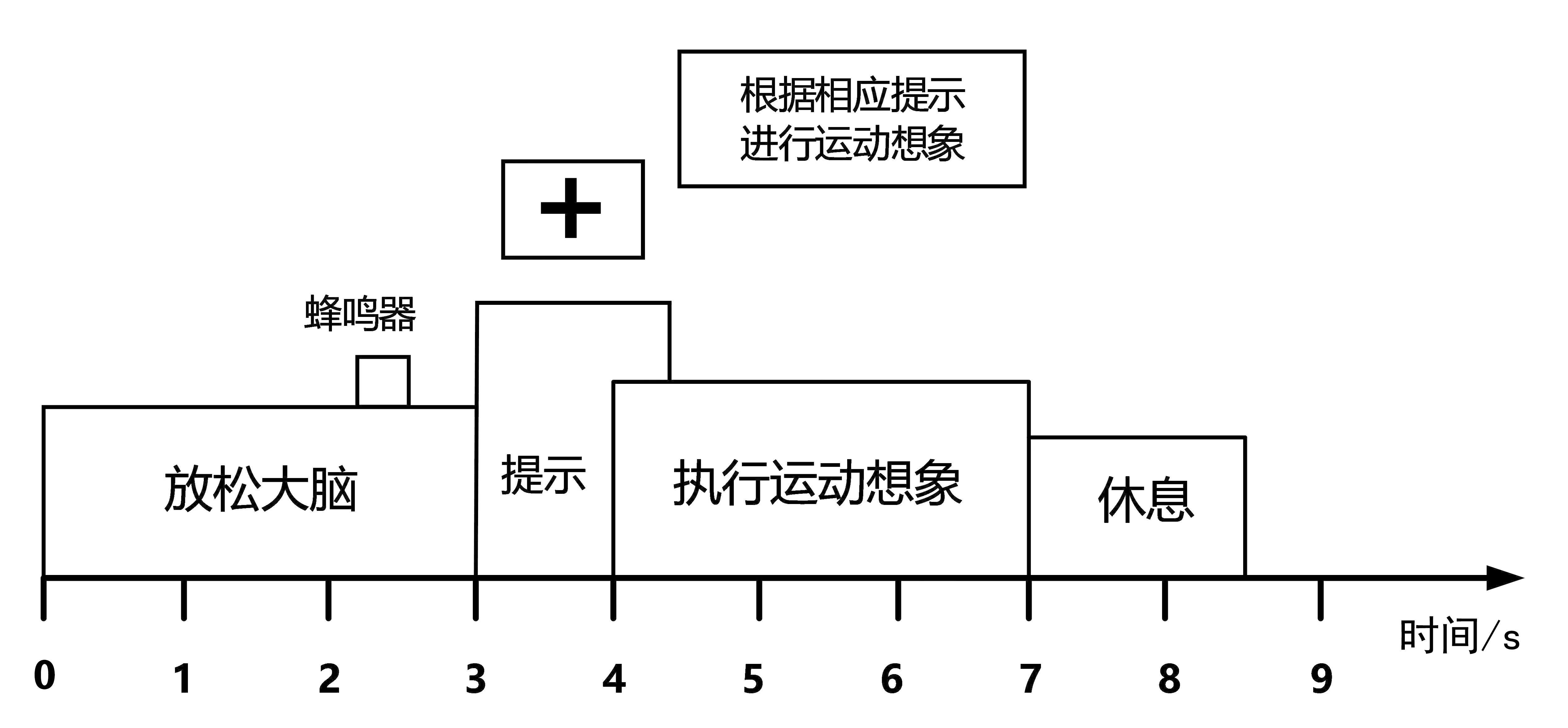
图1 脑电信号采集范式示意图Fig.1 Schematic diagram of EEG signal acquisition paradigm

3 实验论证(Experimental verification)

小波变换和FastICA对脑电信号中的眼电伪迹做融合去噪处理,通过对包含眼电伪迹的原始脑电信号进行两次眼电伪迹去除。在小波变换去噪阶段,选择合理的小波函数以及特定的分解尺度将原始信号分解成不同尺度的小波系数,根据事先设定的阈值,将小波系数中低振幅的部分识别为噪声,并将其抑制。这种方法在保留有用信号的同时,有效地减少了来自环境、电极接触以及肌肉活动等因素引入的干扰,从而提升了脑电信号的质量和清晰度。

根据小波变换的多分辨率特性,使用小波分解重构的方法滤除眼电噪声。低频的眼电噪声能很好地被去除,并且当尺度相似的小波系数选择准确时,眼电噪声的去除受其他因素的干扰很小。高频系数通常代表信号中的细节信息,而低频系数则代表近似部分,包含信号的整体特征。由于噪声通常在低频部分占主导,因此可以通过分析小波系数估计噪声的强度。

针对原始脑电信号设计Symlet-8小波基函数,进行4级小波分解,并启用对噪声标准差的自动缩放。根据脑电信号的数据统计特性和噪声自适应地选择合适的阈值进行去噪,自动确定最佳的阈值,从而实现更好的去噪效果。图2为经过小波变换去噪前后的脑电信号波形对比图。

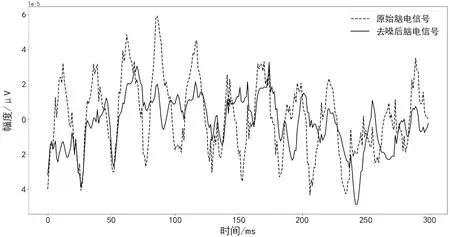
图2 经过小波变换去噪前后的脑电信号波形对比图Fig.2 Comparison diagram of EEG signal waveforms before and after WT denoising

进行小波分解后,可能存在去噪率较低的问题,因此进行小波变换处理后,还要通过FastICA进一步去噪。FastICA可以进一步分离出有用的脑电活动信号和剩余的噪音成分,并从脑电信号中提取出独立分量,对脑电信号进行重构,从而达到对原始脑电信号更有效的去噪效果,获得纯净度更高的脑电信号。仅通过单一小波去噪后的脑电信号波形图如图3所示,图3表示25个通道的脑电波形。

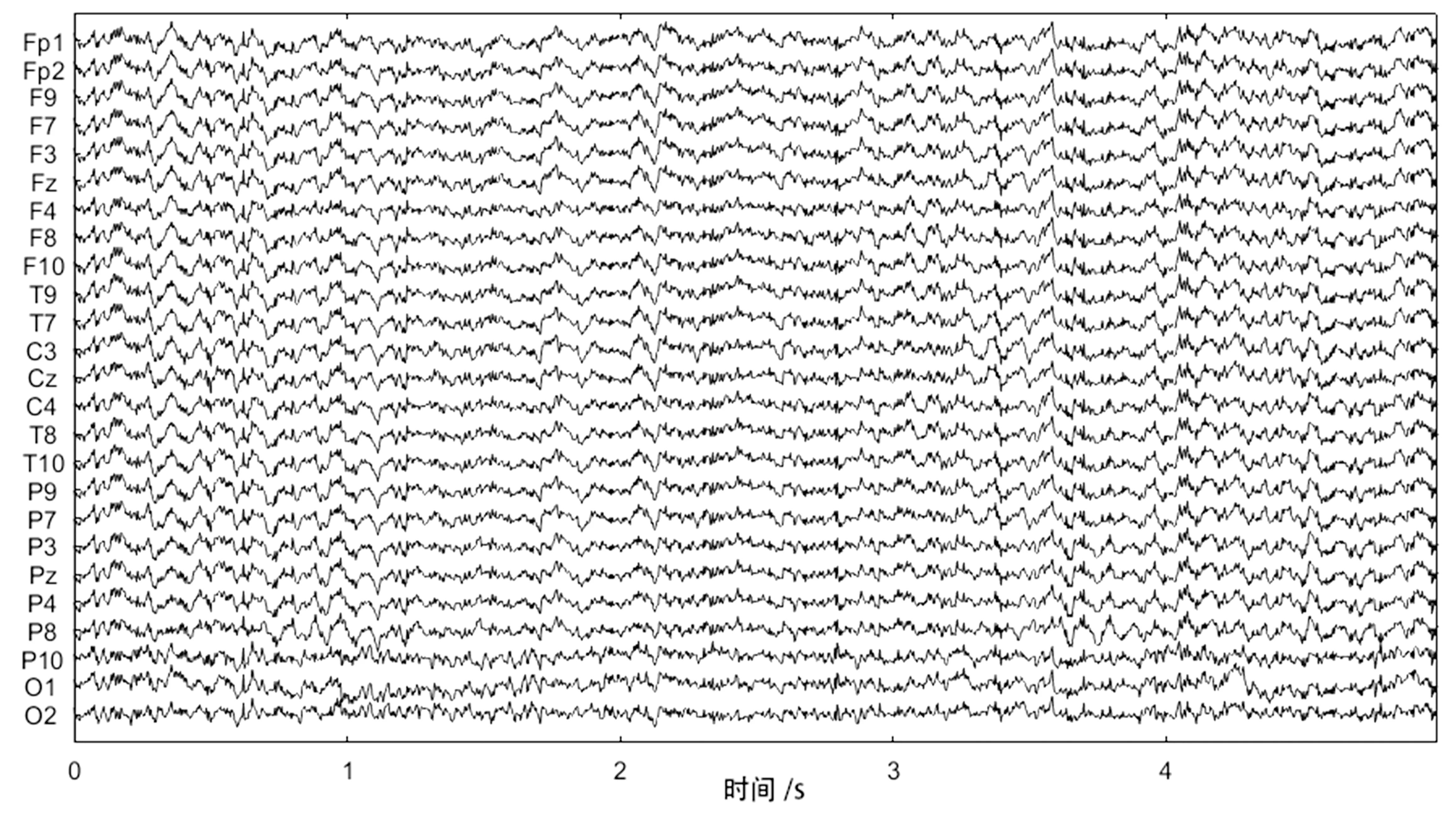
图3 仅通过单一小波去噪后的脑电信号波形图Fig.3 Waveform diagram of EEG signals denoised only by a single wavelet

FastICA分解信号后,以原始脑电信号中的预估眼电成分为参考对分量进行标记后予以剔除,针对分离的独立脑电成分进行重构,生成去噪后的脑电信号。经过WT-FastICA融合处理后的脑电信号波形图如图4所示。

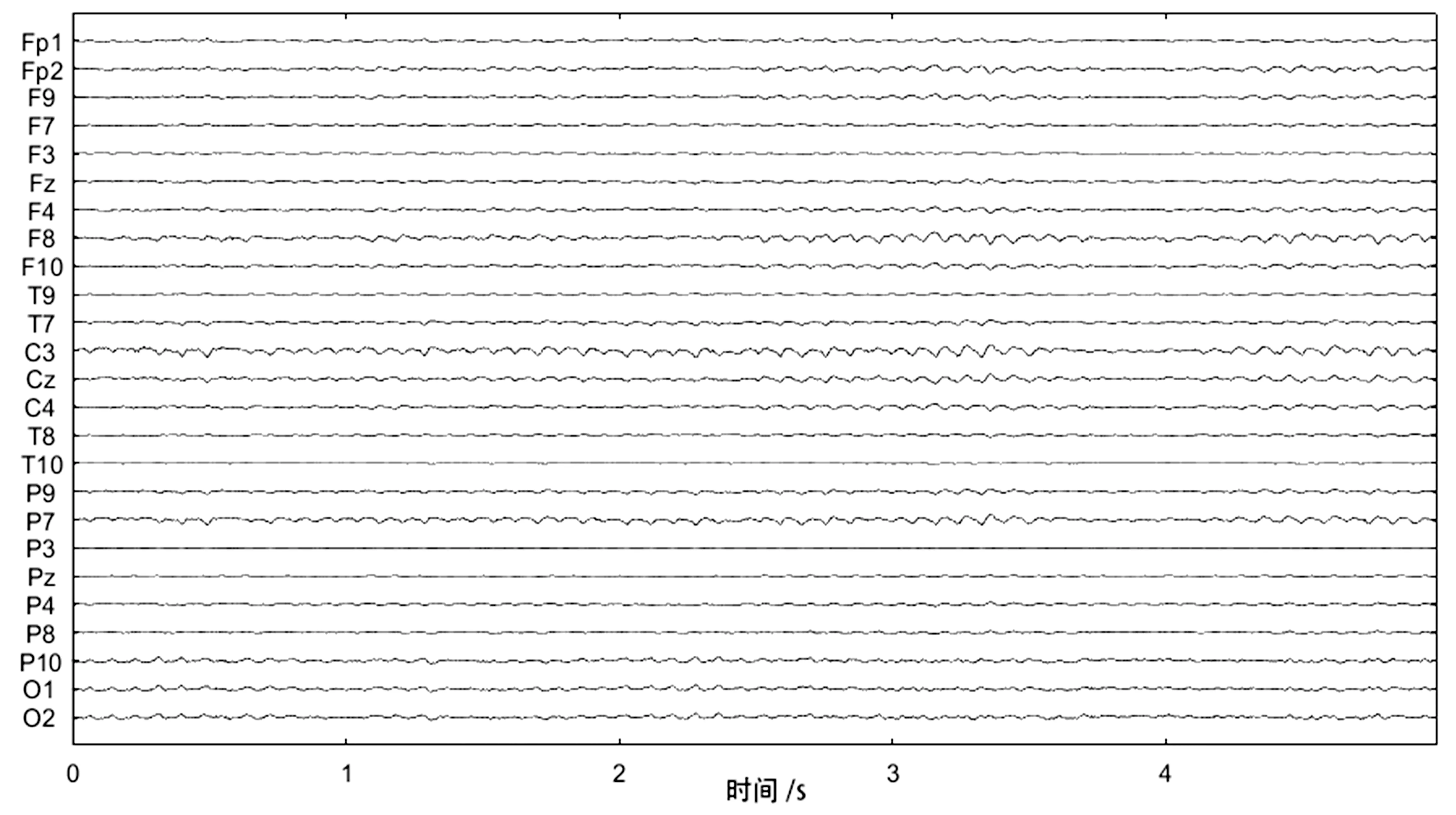
图4 经过WT-FastICA融合处理后的脑电信号波形图Fig.4 Waveform diagram of EEG signals after WT-FastICA fusion processing

采用了基于WT和FastICA相结合的眼电伪迹去除方法,经过一系列算法去噪后,利用经验模态分解进行特征提取,并输入支持向量机(Support Vector Machine,SVM)进行分类结果验证。通过对比文中所提到的小波变换和FastICA算法,验证了本文所提出算法的有效性,其分类识别率结果如表1所示。

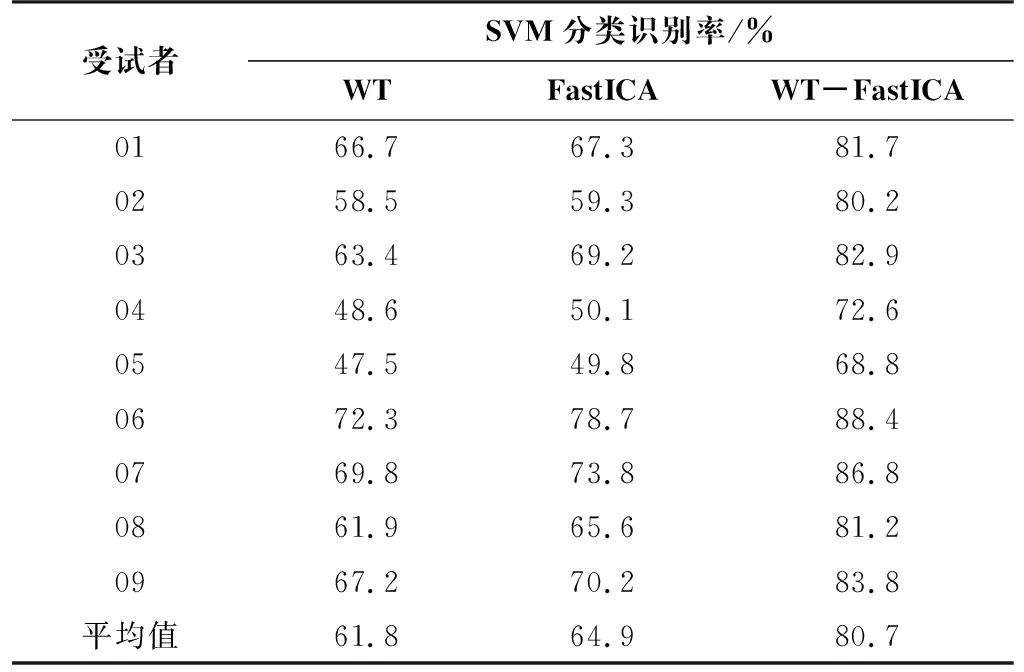
表1 不同去噪算法下脑电信号的SVM分类识别率

由表1可以看出,通过对比三种去噪算法下脑电信号的分类识别率,除第四个和第五个受试者在融合算法作用下的分类正确率略低,与前两种算法的分类结果较为接近外,其他样本都取得了较好的分类效果。从总体来看,针对9组不同的受试者,本文提出的融合算法处理后的脑电信号在经过SVM分类后,分类识别率相较于单一算法分别提升了18.9%和15.8%,去噪效果上要远远优于单一算法。

4 结论(Conclusion)

针对脑电信号中眼电伪迹的消除问题,本文提出一种结合WT和FastICA算法的眼电伪迹去除方法。原始脑电信号经过WT去噪后,再利用FastICA对信号进行重构,最终实现对脑电噪声的过滤。通过实验证明,该方法最终提高了脑电信号的分类精度,并且与单独使用两种基本算法相比,融合算法能够考虑不同受试者的个体差异,充分提取运动想象脑电信号中的频率和空间特征,有效去除了混杂在脑电信号中的眼电信号等噪声伪迹。