服装生产线中基于熟练度的人员调度模型及策略研究

张文豪, 王无双, 王成群,3, 骆淑云,3

(1.浙江理工大学计算机科学与技术学院, 浙江 杭州 310018;2.浙江理工大学信息科学与工程学院, 浙江 杭州 310018;3.东北大学流程工业综合自动化国家重点实验室, 辽宁 沈阳 110004)

0 引言(Introduction)

传统服装制造业的生产模式具有大规模生产的能力,随着近年来消费者对个性化服装定制需求的不断增长,服装企业由大批量的生产模式改为多订单、小批量的新生产模式。在大部分服装企业中,生产计划依然是由管理人员根据经验制订,但是这样的生产计划制订方式不仅效率低下,而且难以应对新生产模式中服装订单需要插单、重新排单等突发状况[1]。在新的生产模式下,服装企业虽然通过机器等工具在生产工序上实现了自动化生产,但是依然有很多工序或机械需要人员操作,而服装生产企业的员工流动性大、技能差异大等因素也导致生产计划需要频繁调整或重新制订,因此急需探索一种具有人员自动调度功能的调度模型用于实际生产。

本文首先针对因人员技能差异造成的服装生产调度问题进行建模,以最小化实际总工序时间为优化目标,并考虑员工熟练度、工序生产平衡率等约束条件的影响;通过对多种经典算法性能进行比较分析发现,遗传算法能够较好地解决该问题。其次使用服装厂的实际数据对本文设计的模型进行性能评估,并与遗传算法(Genetic Algorithm, GA)、贪心算法(Greedy)、粒子群算法(Particle Swarm Optimization, PSO)等经典算法进行了对比。为了进一步评估本文设计的模型在不同问题规模下的通用性,分别在不同规模的工厂调度场景下进行算法的模拟仿真实验。最后利用生产任务甘特图对调度流程进行可视化呈现,进一步验证本文所提方法能够保证企业平稳有序地生产。

1 研究现状(Research status)

随着智能制造的发展,企业的生产逐步向智能化、自动化方向转变。为了满足市场上个性化的需求,企业开始由大批量的生产模式转变为多订单、小批量的新生产模式。在实际生产中,影响服装生产效率的因素众多,如服装款式差异、加工设备差异、订单批量差异等,很多学者对不同的影响因素进行了大量研究[2]。针对加工顺序、工位分配的差异性,刘锋等[3]提出了基于深度强化学习的实时动态调度方法,解决了现有服装生产调度过程中,动态事件自适应及实时响应能力差的问题。该方法在调度目标达成度上稍差于遗传算法,但大幅减少了决策时间。针对加工顺序、加工设备的差异性,谢子昂等[4]提出了一种基于多目标动态调度算法的自适应滚动窗口机制调度模型,并运用非支配遗传算法对模型进行求解,解决服装大规模定制生产的自适应性较弱的问题。针对订单的差异性,李彬彬[5]提出了面向订单的服装企业的生产作业计划的数学模型,利用遗传算法进行了求解。郑卫波等[6]建立了企业生产模型和计划编制的目标函数,同样采用遗传算法对问题进行了求解。针对所需服装数量、铺布能力和裁剪顺序的限制,WONG等[7]提出了双层调度模型,解决了服装行业中的混合流水车间和早晚调度问题。针对服装部件匹配周期的差异性,谢子昂等[8]构建了部件同步生产模型,采用遗传算法优化了订单的投产安排,减少服装部件匹配时间和调动次数,并进行了模拟仿真。针对生产线平衡能力的差异性,张旭靖等[9]建立以最小化平衡损耗率为目标的平衡优化模型,利用遗传算法解决服装缝制生产线作业间由不平衡产生的效率损失问题。

针对服装生产效率的影响因素,目前还没有学者深入研究服装生产人员技能差异对生产调度计划制订带来的影响。因此,本文针对服装生产线中基于熟练度的人员调度影响因素研究了人员调度模型及策略以优化服装厂生产调度计划。

2 服装生产线人员调度模型(Personnel scheduling model of garment production line)

2.1 调度问题描述

服装企业需要解决的问题是在保证员工合理的工作时间和生产线平衡率的同时,以缩短生产时间为目标,制订订单生产调度计划。在服装厂生产调度计划制订过程中,该调度问题可以被描述为有n个订单(D1,D2,…,Dn),由一组拥有m名员工(s1,s2,…,sm)的加工小组进行加工,任一订单Di由加工顺序已知的工序Pi={Pij,j∈(1,2,…,ni)}组成,订单Di的第j道工序可选员工序号集合为Sij⊆{1,2,…,m},(1≤i≤n,1≤j≤ni),员工sk加工订单Di的第j道工序的熟练度为Eij={Eijk,k∈(1,2,…,m)}。调度目标是将所有订单中不同的工序分配给员工,以实现所有订单实际总工序时间最小化。

2.2 符号定义

订单Di的第j道工序为Pij;工序Pij的标准加工时间为Tij;工序Pij的实际加工时间为Tijk,其公式如下:

(1)

员工sk的实际加工总时间为Tsk,其公式如下:

(2)

生产计划的平均工序时间为t,其公式如下:

(3)

平均工序时间t由所有员工的工作时间决定。生产调度过程中希望每名员工的总工作时间都接近平均工序时间以平衡各自的生产进度;平衡率α是平均工序时间t与员工最大实际加工总时间之间的比值,用来评估整个加工过程工序堵塞堆积的情况,其公式如下:

(4)

2.3 调度模型

2.3.1 优化目标

本研究以实际总工序时间T最小化为优化目标,其公式如下:

(5)

2.3.2 约束条件

由于在服装厂的实际生产过程中,个别员工对整个生产过程中的大多数工序都具有较高的熟练度,如果将这些工序全部分配给这名员工,会导致多个不同部件的工序无法进行并行生产的情况,进而影响整个生产过程的效率,因此服装厂需要尽可能地平衡每名员工被分配到的工序总时长Tsk。

公式(6)表示为了提高平衡率α,需要约束员工被分配到的最大工序总时长max(Tsk)。公式(7)表示一道工序只能由一名员工进行加工,其中Xijk为工序Pij是否由员工sk进行加工的判别条件,当将工序Pij分配给员工sk进行加工时,Xijk=1,反之为0。公式(8)表示工序加工顺序的约束条件,TBijk、TWijk分别为工序Pij由员工sk进行加工的实际开始时间和加工完成后的实际总工序时间。

max(Tsk)≤t(1+β),k∈Sij,β≥0

(6)

(7)

TWijk≤TBi(j+1)k,k∈Sij

(8)

β是设定的抖动率参数,用于约束每名员工的总工作时间。

3 基于熟练度的人员调度策略(Proficiency-based personnel scheduling strategy)

3.1 基于熟练度的人员调度策略构建

传统的服装生产调度方式是按前片、后片、袖子、袖口等部件顺序生产,所有部件加工完成后,再进行组合工序生产,具体工艺流程如图1所示。基于熟练度的人员调度策略,首先搜索工艺流程图中从部件生产开始到结束的所有路径,比较所有路径的工序生产标准加工总时间,其次将标准加工总时间最多的路径作为最佳路径,并将其他的生产路径与最佳路径并行生产,最后根据员工对工序的熟练度进行分配。当在某一时刻,最佳路径的工序与并行路径的工序需要同一名员工生产时,则适当调整并行路径的工序开始时间,保证生产流水线畅通,并减少服装生产时间。

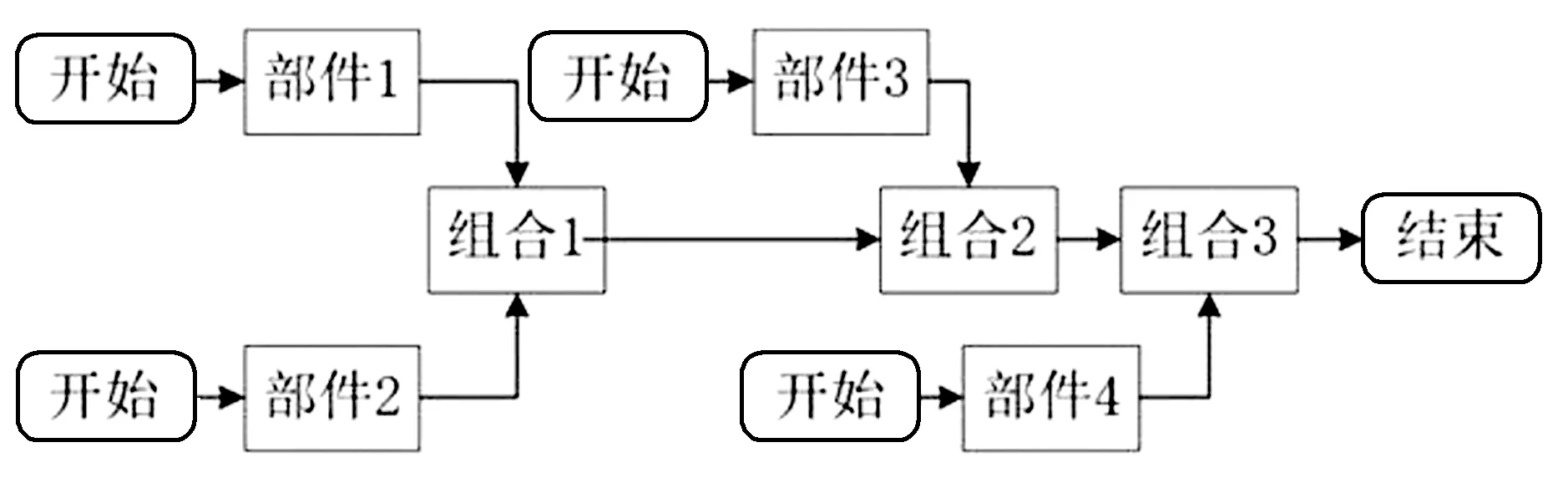
图1 工艺流程图Fig.1 Process flow chart

3.2 基于遗传算法的人员调度方法

遗传算法是一种非确定性的拟自然算法,为复杂系统的优化提供了一种新思路,在诸多领域均有很好的应用效果,如函数优化、组合优化、生产调度等[10]。与其他经典优化算法相比,遗传算法并不是直接对问题本身进行优化,而是通过对问题进行编码,并且以适应度函数评价解的优劣,避免无法得到问题的解。遗传算法专注于搜索范围,以初始种群为搜索对象,能够同时搜索多个点,并最终提高算法的求解效率。服装厂人员调度过程中需要同时考虑多个约束条件对调度目标的影响,本文借助遗传算法良好的全局搜索能力和求解效率,对生产线人员进行调度优化。

3.2.1 染色体编码

本文构建了一个一维数组,采用基于数组的实数编码方法,染色体中的基因代表对应工序所安排的员工序号。

3.2.2 遗传算法设计

基于遗传算法对生产线人员进行调度优化,算法设计实现过程如下。

(1)生成初始种群:按照上述染色体表示方法,每道工序不选择熟练度为0的员工,排除不可行解后,随机生成数组码,然后构成相应的染色体,形成初始种群。

(2)适应度函数:以实际总工序时间T为目标函数,将其倒数作为适应度函数。

(9)

(3)选择:选择优秀的个体传给下一代。本文采用轮盘赌选择方法,每个个体被选择的概率与其适应度值有关,适应度值越大,被选择的概率越大。

(4)交叉:遍历一对父系染色体的基因,随机产生一个概率Pc,如果这个概率大于Pc,则交换对应位置两个父系的基因。

(5)变异:使用随机变异的方法。取一个随机概率,如果随机概率小于设定的变异概率,随机选择一个位于区间[1,n]的基因aj进行变异,从而形成一个新的子代个体。

(6)重复“步骤(2)”至“步骤(5)”,直到满足算法终止条件,输出最优结果。

3.3 基于粒子群算法的人员调度方法

粒子群算法初始化为一群随机粒子(随机解),然后通过迭代找到最优解。在每一次迭代中,粒子通过跟踪两个“极值”更新自己:第一个极值是粒子本身找到的最优解,即个体极值pbest,另一个极值是整个种群找到的最优解,即全局极值gbest。

3.3.1 粒子群算法设计

(1)生成初始种群:每道工序不选择熟练度为0的员工,排除不可行解后,初始化所有粒子及其速度和位置,并将粒子的历史最优解pbest设为当前位置,而群体中最优解的粒子作为当前的gbest。

(2)适应度函数:以实际总工序时间为目标函数,将其倒数作为适应度函数。

若粒子当前的适应值比之前记录的该粒子历史最优解pbest更好,则更新pbest。

若粒子当前的适应值比之前记录的全局最优解gbest更好,则更新gbest。

(3)粒子根据如下公式更新自己的速度和新的位置:

v(k+1)=ωv(k)+c1r1(pbest(k)-present(k))+c2r2(gbest(k)-present(k))

(10)

present(k+1)=present(k)+v(k+1)

(11)

其中:v(k)是k时刻的速度,present(k)是k时刻的位置,r1和r2是取值范围(0,1)的随机数,ω是惯性权重因子,c1和c2称为加速因子或学习因子。

3.4 基于贪心算法的人员调度方法

贪心算法是一种只考虑当前对自己最有利的选择,通过逐步获得最优解解决最优化问题的一种算法。

3.4.1 贪心算法设计

(1)根据工艺流程对每道工序选择其熟练度最高的员工,当有多个熟练度相同的员工可以选择时,随机选择其中一名员工,生成初始解。

(2)计算初始解,即每名员工的实际加工总时间,对每道工序根据最大工序时间进行迭代优化。

(3)重新遍历所有工序,如果当前工序所安排员工的实际加工总时间超出最大工序时间,并且当前工序有其他熟练度较高且实际加工总时间小于最大工序时间的员工可以选择时,将当前工序分配给实际加工总时间短的员工。

(4)重复以上步骤,直至所有员工的总加工时间满足最大工序时间,或者达到设定的循环次数时,结束循环,输出当前的最优结果。

4 实例仿真及性能评估(Example simulation and performance evaluation)

4.1 工厂数据集性能评估

4.1.1 服装企业背景

本文以杭州某服装厂为例。为了满足市场需求,服装厂的生产模式由原来的大批量生产转变为多订单、个性化小批量生产。由于订单之间存在差异,所以服装厂每接一个订单就需要制订对应的生产计划。

4.1.2 工艺数据

本文以生产连衣裙为例,需要生产的裙子分为前片、后片、袖子、袖口、襟贴、耳仔、腰带、配件等部件,每一个部件都需要经过多个工序加工后组合成成衣,生产工艺如图2所示。一个生产小组的员工人数为19人,所做的服装有8种部件,其中前片部件有21道工序,后片部件有11道工序,袖子部件有15道工序,袖口部件有5道工序,襟贴部件有10道工序,耳仔部件有5道工序,腰带部件有7道工序,配件有6道工序,最后将所有部件组合环节又有40道工序,即生产一条连衣裙总共需要120道工序。每名员工对每道工序的熟练度由员工熟练度表(表1)计算得出,表1中熟练度由服装厂管理人员考虑员工对各种工序的熟练程度、身体状况等因素按百分制进行量化,在实际计算过程中,将数值转化为小数带入模型中计算。每道工序的标准时间由款式工序表(表2)得出。

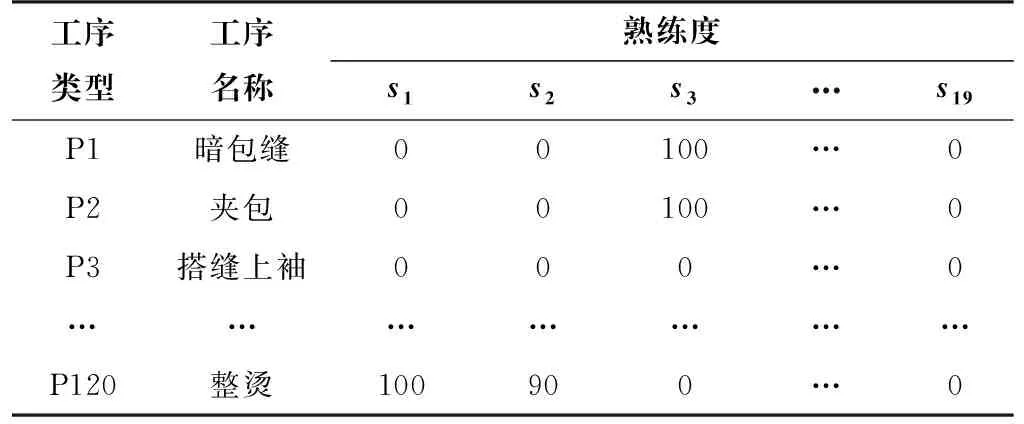
表1 员工熟练度表

表2 款式工序表

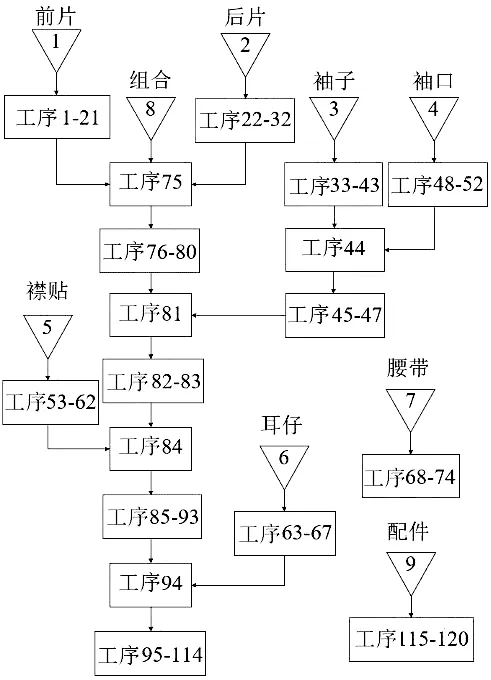
图2 连衣裙生产工艺流程图Fig.2 Process flow chart of skirt production

4.1.3 算法参数设置

为兼顾算法收敛速度和解集质量,算法设置种群规模为30,最大迭代次数为500次。遗传算法变异概率Pm和交叉概率Pc在经验范围内选择,本文设置Pm=0.02、Pc=0.5。

4.2 仿真结果分析

对比遗传算法、粒子群算法、贪心算法的实验结果,开展50次实验,生产一件成衣的实际总工序时间、最大工序时间、算法的运行时间的平均结果如表3所示。此时,完成生产的平均时间为2 909.5 s,与服装工厂原先的4 814.4 s相比,生产效率提升约39.6%,且遗传算法明显优于贪心算法和粒子群算法。

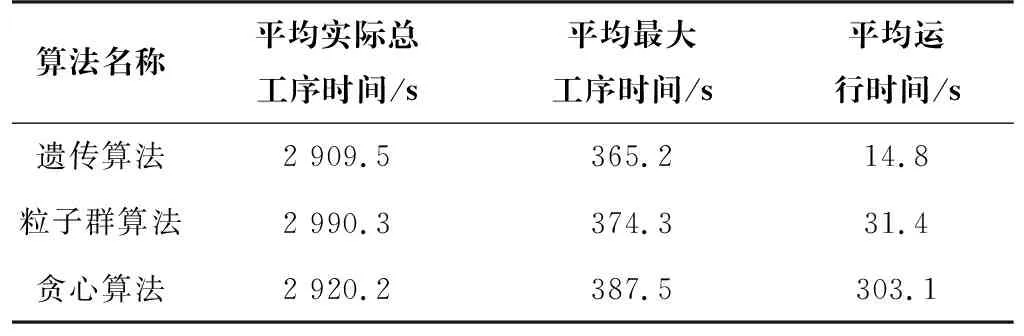
表3 引入抖动率和基于熟练度的人员调度策略的实验结果

为了得到合适的抖动率,本文分别在抖动率为0～100%的情况下,对实际总工序时间和最大工序时间进行了对比分析,结果如图3、图4所示。当设定的抖动率在60%～100%时,抖动率越小,实际总工序时间越长,对应的最大工序时间越短;反之,抖动率越大,实际总工序时间越短,对应的最大工序时间越长。但是,当抖动率小于60%时,在设定的最大迭代次数内,算法可能无法求解出小于设定的抖动率的解,此时输出优化后的当前最优解,如图3、图4中抖动率为0～50%时所示。因此,服装厂可根据实际情况选择合适的抖动率,当服装厂需要生产线的生产时间更短,可以设置较高的抖动率,以获得更短的实际总工序时间。经过多次实验得出结论,如图5所示,当设定抖动率为60%时,实验结果标准差相对最小,稳定性最高。

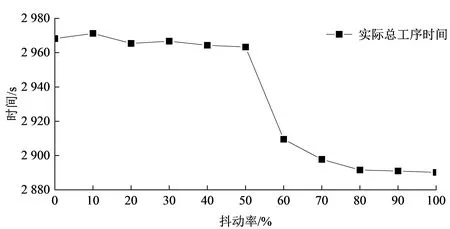
图3 遗传算法在不同抖动率下的实际总工序时间Fig.3 Actual total process time of GA under different jitter rates

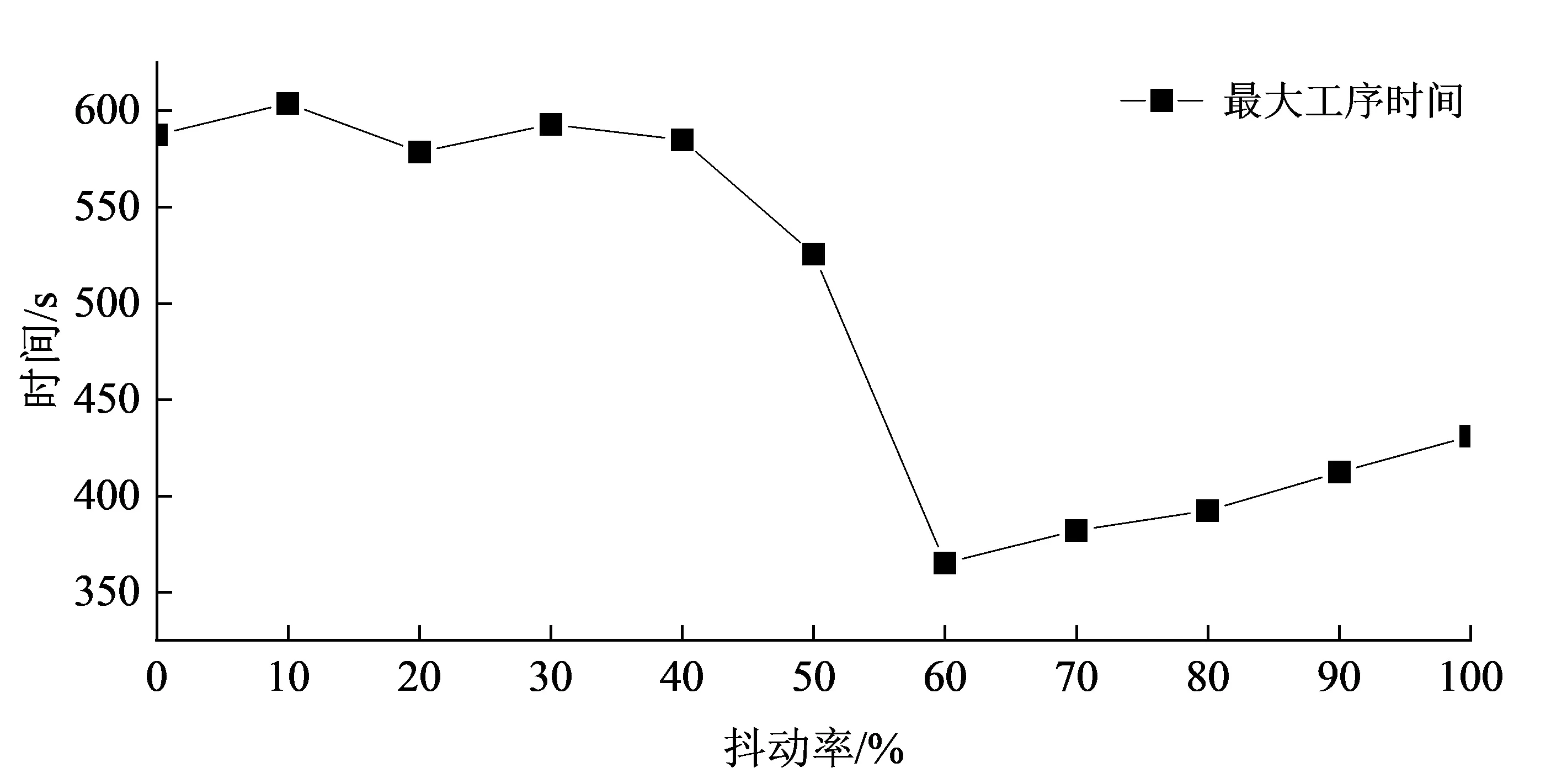
图4 遗传算法在不同抖动率下的最大工序时间Fig.4 Maximum process time of GA with different jitter rates

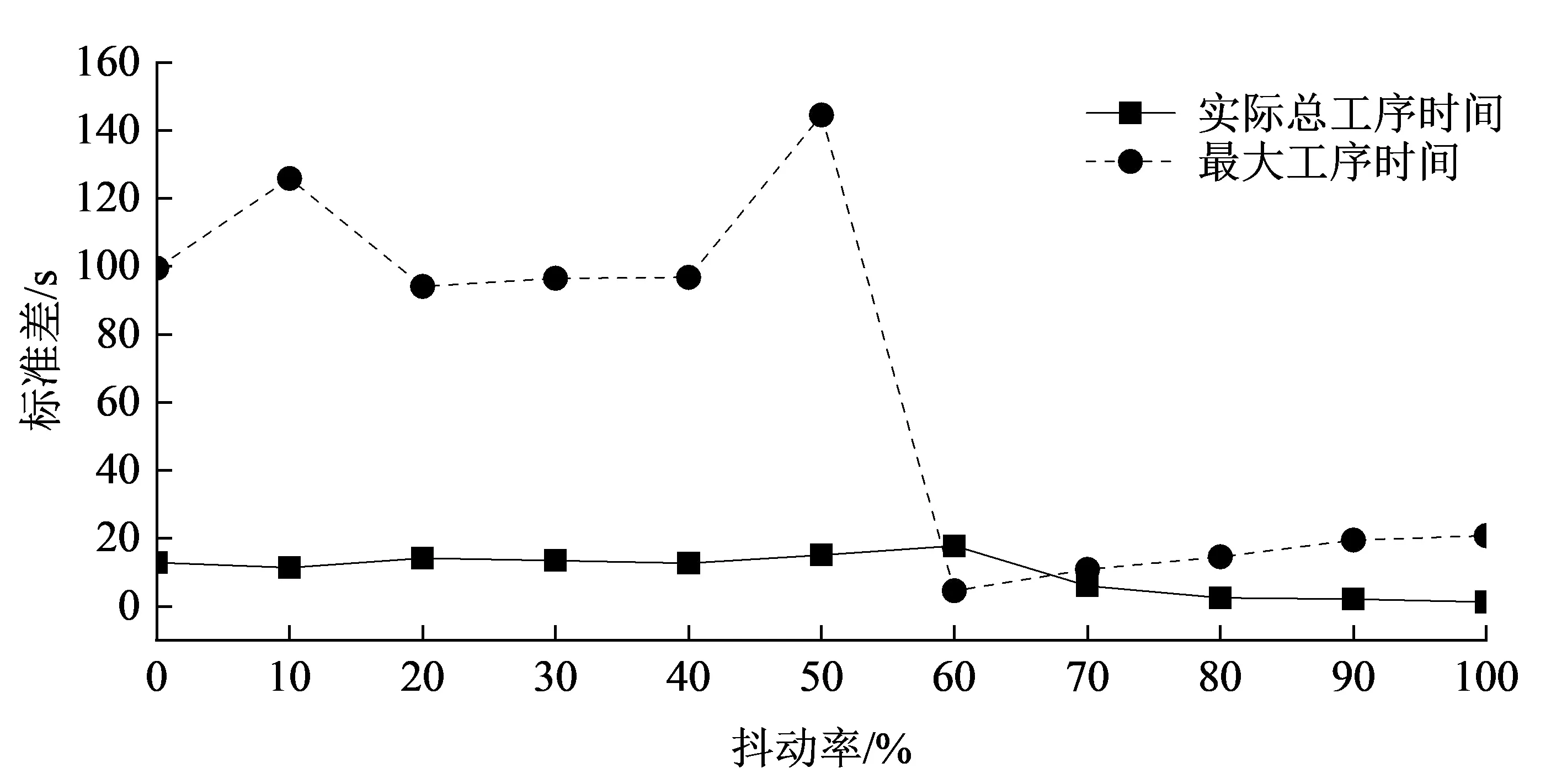
图5 实际总工序时间与最大工序时间的标准差Fig.5 Standard deviation of actual total process time and maximum process time

研究得出基于熟练度的人员调度策略优化后的调度结果甘特图(图6)。从图6中可以看出,前片和组合工序为生产工艺流程图中的最佳路径工序组合,可以将其余的工序与之进行并行生产。当最佳路径工序组合与并行的工序需要同一员工进行生产时,可以延后并行工序的开始时间,确保生产过程平稳有序。

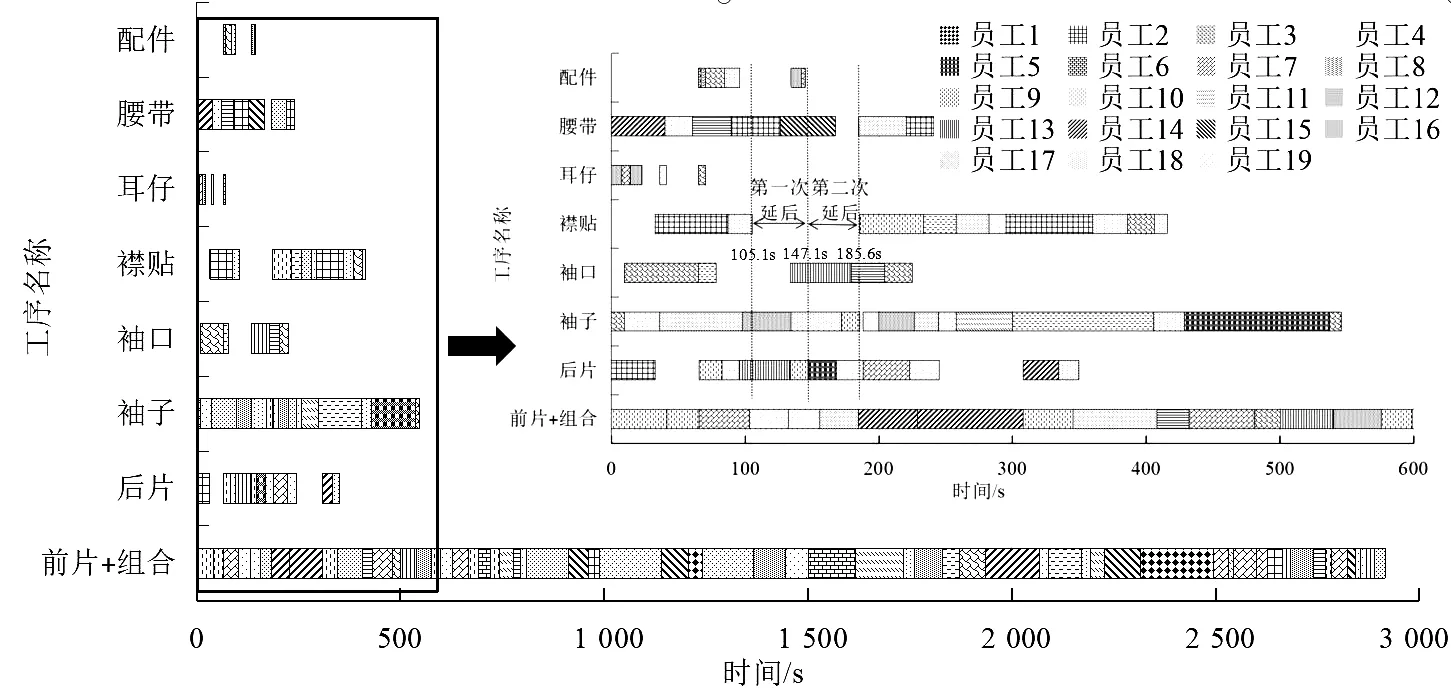
图6 基于熟练度的人员调度策略优化后的调度结果甘特图Fig.6 Gantt chart of scheduling results after optimization of personnel scheduling strategy based on proficiency

4.3 不同规模场景性能评估

4.3.1 工厂调度问题的规模定义

中小规模调度问题规模一般不超过20台机器、50个工件[11]。在文献[12]中将大规模生产调度问题分为以下几种情况:设机器数为M,工件数为J:(1)M>20,J>50;(2)M>20,J≤50时,M×J>1 000;(3)M≤20,J>50时,M×J>1 000。

4.3.2 不同规模场景实验结果

本文分别对不同规模的数据场景进行验证和算法对比。为兼顾算法收敛速度和解集质量,算法均设置最大迭代次数为500次,设员工数为S,工序数为P。在相同的抖动率下,50次实验实际总工序时间、实施策略优化后的实际总工序时间、最大工序时间、运行时间的平均结果如表4所示。实验结果表明,在部分规模场景下,遗传算法在实际总工序时间上稍差于粒子群算法,但最大工序时间和运行时间明显优于其他算法。

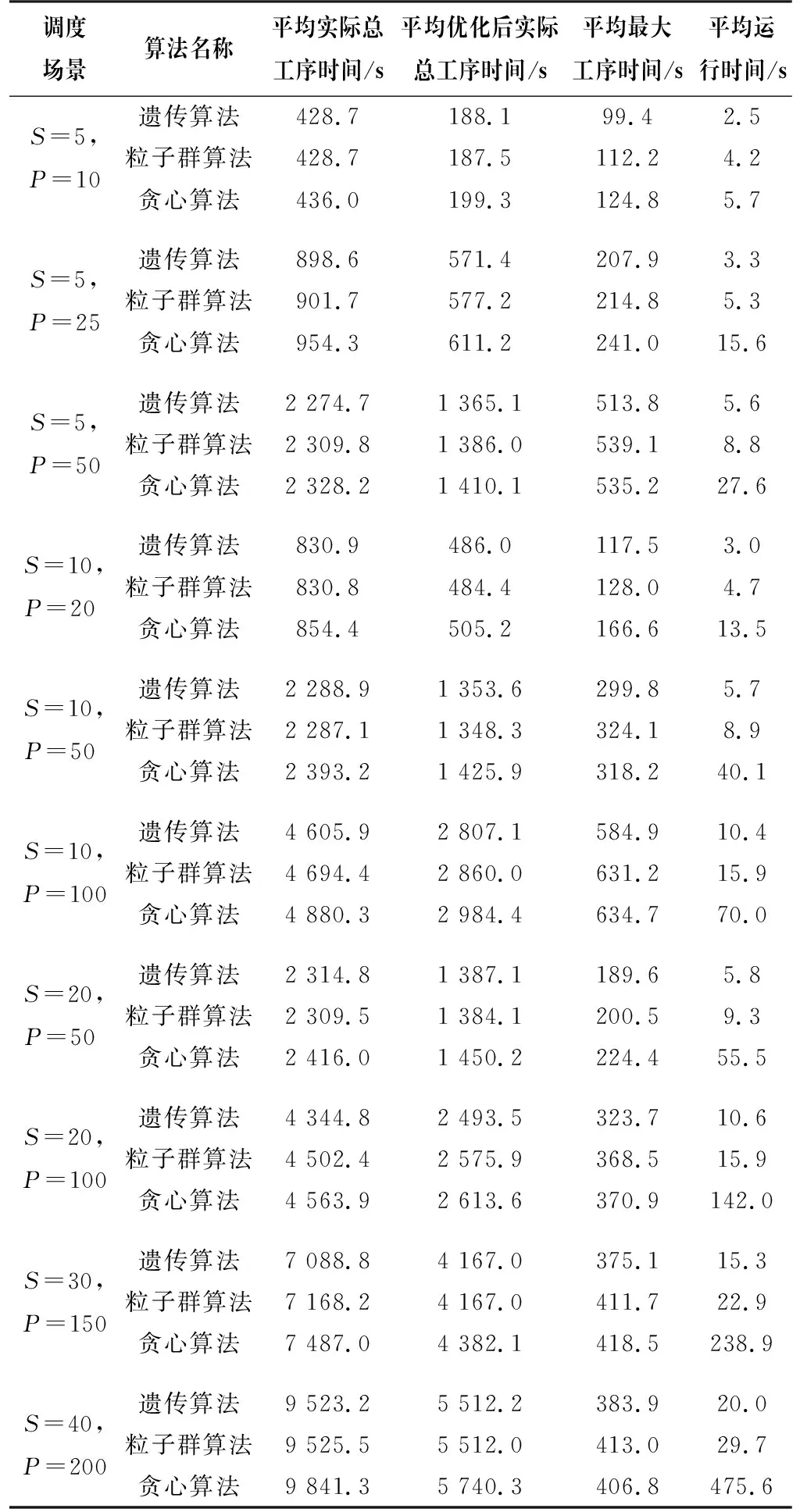
表4 不同规模场景下算法对比结果

5 结论(Conclusion)

本文首先针对服装生产线中现有的人员调度问题进行建模,其次提出了基于熟练度的人员调度策略和基于遗传算法的人员调度方法对该问题进行求解,最后采用服装厂实际生产数据对策略方法进行验证。实验证明,本文提出的策略与方法能够有效地解决服装生产线中的人员调度问题,提高生产线生产效率。此外,为了验证本文所提出的策略与方法在不同规模场景下的有效性,开展了实验进行策略的性能评估,实验结果表明,在部分规模场景下,遗传算法在实际总工序时间上稍差于粒子群算法,但最大工序时间和运行时间明显优于其他算法。