考虑次品处理的液压缸制造车间动态调度研究
2023-12-06唐红涛杨基源张雁翔
唐红涛,杨基源,张雁翔,张 伟
(1.武汉理工大学 机电工程学院,湖北 武汉 430070;2.韶关液压件厂有限公司,广东 韶关 512000;3.机器人与智能制造湖北省工程研究中心,湖北 武汉 430070)
液压缸制造车间调度问题属于典型的柔性作业车间调度问题(flexible job-shop scheduling problem, FJSP)。不良品检验以及次品处理是液压缸零部件生产中不可或缺的环节,而由于液压缸“多品种,小批量”的生产模式以及其零部件毛坯价值较大等因素,导致次品处理在液压缸生产过程中难以避免。次品处理程序使得原有加工需求发生变化导致初始调度方案不再最优,同时由于员工熟练度、机床老化等因素导致实际生产中次品处理常发,因此急需研究考虑次品处理的液压缸制造车间调度问题。
FJSP是经典JSP(job-shop scheduling problem)的扩展,它允许给定集合的机器完成加工[1]。近年来有很多FJSP的扩展研究,如带模糊加工时间的生产调度[2]、多目标车间调度[3]、分布式车间调度等[4]。而在应用中动态柔性作业车间调度问题(dynamic flexible job-shop scheduling problem, DFJSP)与实际环境更相似,能够满足不断变化的车间环境[5]。如机器发生故障,使可用机器数量减少,从而导致原调度过程需要调整[6]。Nouiri[7]通过改进PSO(particle swarm optimization)算法解决了考虑能耗的动态柔性作业车间调度问题。高开周等[8]提出中断和释放的已调度任务来解决紧急订单问题。吴正佳等[9]针对故障机器剩余工件构建了约束模型,提出了重调度方法。汪俊亮等[10]针对加工时间不确定的FJSP,采用冗余处理方法构建模型。
帝国竞争算法(imperialist competitive algorithm, ICA)是一种受社会和历史的进化而启发的群智能优化算法[11]。针对ICA收敛过快易陷入局部最优等问题,Lin等[12]提出摄动同化运动和边界反弹改进了帝国同化方式。
1 柔性作业车间动态调度模型
FJSP可以描述为n个工件安排在m个机器上加工,每个工件有若干工序,确定加工方案来保证整体加工目标值最优。DFJSP可以视为在FJSP的基础上考虑扰动因子。笔者将次品处理扰动分为4类,具体如表1所示。相关变量符号及定义如表2所示。

表1 次品处理动态扰动因素

表2 变量描述
决策变量如下:
δijk:若工序Oij在机器k上加工为1,否则为0;
Fij:若工序Oij发生返工为1,发生返修为2,发生重投为3。
目标函数为:
minCmax=min[max(Cj)]
(1)
(2)
(3)
约束条件如下:
(4)
Ci(j+1)k-Pi(j+1)k+M(1-δi(j+1)k)≥Cijk∀i,j,k
(5)
Cijk≤Sghk+M(1-γijghk) ∀i,j,g,h,k
(6)
Cijk=Sijk+Pijk∀i,j,k
(7)
当Fij=1或Fij=2时:
Ci(j+1)k-Pi(j+1)k+M(1-δi(j+1)k)≥Ci′j′kδijk=1
(8)
当Fij=3时:
(9)
式(1)为最大完工时间Cmax最小;式(2)为在制品库存γ最小;式(3)为动态调度扰动量ω最小,体现了动态调度给生产系统带来的额外任务量;式(4)为一道工序只能被一台机器加工;式(5)为工序加工顺序约束;式(6)为一台机器同时只能加工一道工序;式(7)为加工不可中断;式(8)为次品处理工序的加工顺序约束;式(9)为重投后所有工序重新加工。
2 改进帝国竞争算法
2.1 编码和解码
FJSP采用双层编码即工序排序(operation sequence,OS)和机器选择(machines selection,MS)两部分,如图1所示。OS部分中工件i第j次出现代表工序Oij,对应的MS部分为其加工的机器次序。
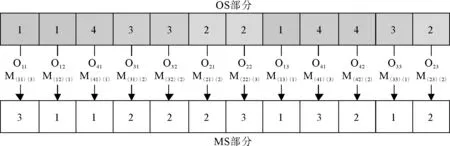
图1 3×3规模问题编码举例
2.2 改进ICA算法
2.2.1 初始化国家
设置国家数量Npop、帝国数量Nimp等参数。引入Logistic 混沌映射迭代方程来完成初始化,映射迭代方程为:
y(k+1)=μy(k)(1-y(k)),k=1,2,…,n
(10)
式中:y(k)、y(k+1)分别为第k次、第k+1次混沌映射迭代中该编码处的随机数;μ为方向参数。
定义个体维度为m,种群规模为N,随机生成m维初始序列z1=(z11,z12,…,z1m),通过式(10)迭代从而得到初始混沌序列矩阵zlo。将zlo通过式(11)变换到目标问题的变量区间上,从而完成初始混沌映射。
xij=uj+zij(vj-uj)
(11)
式中,vj和ui分别为第j维变量取值的上界和下界。
2.2.2 构建初始帝国
针对多目标优化问题,给出了一种简化的帝国初始化机制,步骤如下:
步骤1对种群Npop进行Pareto非支配排序,得到大小为n的第一前沿解集Π;
步骤2如果第一前沿解的数量n<算法所定的帝国数量imp,则对Π进行局部搜索生成外部种群Nn,将Nn放入种群Npop中,执行步骤1;否则执行步骤3;
步骤3随机选择Π中的imp个个体为殖民国家,由式(12)可计算帝国分配的殖民地数。
(12)
式中:NCi为第i个帝国中的殖民地数量;pop为所有国家数量;a为随机参数。
步骤4:将Npop中剩余的col个个体按Rank等级排序,并交替分配给殖民国家。
2.2.3 帝国同化
引入文化入侵概念,即殖民地在向殖民国家同化时,有一定概率向其他殖民国家学习。步骤如下:
步骤1殖民地kcol,与其殖民国家同化得到子代k1,若k1是的kcol非支配解,则保留k1;
步骤2随机选择殖民国家,使kcol与之同化得到子代k2,若k2支配kcol,则保留;
步骤3在k1和k2均存在的情况下,取随机数χ和文化入侵概率ε,若χ<ε,则k2取代kcol;反之,则k1替代kcol作为新的殖民地。
同化采用POX(precedence operation crossover)交叉,引入同化因子δ,通过影响转移长度β来控制同化程度。ρ为(0,1)之间的随机数。
(13)
(14)
式中,It和MaxIt分别是当前迭代数和总迭代次数。
2.2.4 帝国革命
针对帝国革命,设计了一种多层级反馈的邻域搜索算子,按照复杂度把算子分为SNS(simple neighborhod search)、HNS(hard neighborhod search):
SNS计算简单,能够快速突变。
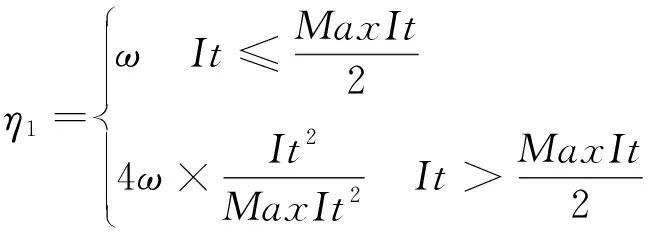
(15)
SNS2:随机选择两道工序a和b,将工序b插到工序a之前,MS部分随之变化。
SNS3:随机选择两个工序,并反转两个位置的OS部分和MS部分。
HNS比SNS更为复杂,它在当前方案关键路径的基础上做变换。
设计两种HNS结构,具体如下:
HNS1:针对关键路径工序,使关键工序的加工机器突变,直到得到非支配解。
HNS2:选择一道关键工序,将其与其他工序做工序交换,若得到非支配解,则替换;否则继续搜索,直到到达搜索上限g1,退出。
帝国革命详细步骤如下:对于殖民地个体kcol,引入革命概率η2,革命若发生,针对kcol做SNS 3种搜索,若产生非支配解k1,则k1替换kcol并终止革命;若无,则革命失败。
对于殖民国家个体kimp,首先对kimp依次做SNS搜索若产生非支配解k1,则k1替换kcol并终止革命;若无且达到搜索上限g2,则对kimp做HNS搜索,若没有非支配解的产生,则革命失败;且之后该殖民地跳过SNS,直到kimp发生变化才恢复对kimp做SNS搜索。
2.2.5 帝国竞争
1.2.5 A 在进行工作过程中,管理人员应当根据实际情况对护理工作的开展进行分析,认真分析门诊感染控制中存在的问题,总结护理结果,并根据标本的控制状况对标本管理计划进行完善。通过持续改进的方式,能够有效的对管理期间的标本管理状况进行分析,从而对管理方案进行改善。通过周而复始的实施,达到循环的目的。
笔者设计了一种保护最弱帝国策略。个体k的成本值ck可用式(16)进行计算:
(16)
(17)

TCP为帝国p的总成本,ξ为系数,一般取0.1。NTCP为归一化成本,EPP为帝国P的势力。
(18)
NTCp=2×max(TC)-TCp
(19)
(20)
式中:cimp为帝国p中殖民国家的势力值;cj为帝国p中殖民地的势力值。
具体步骤如下:
步骤1对所有帝国按势力值排序,势力值最大的帝国不参与竞争。
步骤2取最差帝国的最差个体kwor。
步骤3生成一组随机向量[EP2-r2,EP3-r3,EP4-r4,…,EPimp-rimp],其中r为随机数,取向量最大值对应的帝国l。
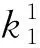
3 仿真结果分析
为测试改进ICA算法求解性能,进行实验验证,经正交实验得到算法参数设置为:种群规模population=50,最大迭代次数MaxIter=100。初始帝国数量Nimp=10,HNS搜索最大迭代次数g1=10,入侵概率ε=0.3。
采用 Brandimarte数据集中的8个标准经典算例(MK01~MK08)扩展算例进行策略对比分析[13]以及某液压件厂实际案例进行算法分析。
3.1 改进策略有效性分析
笔者设计了8个策略组合算法来分析改进策略的有效性,如表3所示,每个算法采用相同参数,独立运行MK01-MK08各10次。运算结果如表4所示,分别带有改进策略的IICA-1~IICA-3在两个目标上的平均值Avg和最优值Best均小于初始ICA算法值;能够证明策略的有效性。

表3 策略分配

表4 算法结果对比
3.2 算法对比分析
分别与现有文献中的灰狼算法[14]、改进遗传算法[15]、粒子群算法[16]、人工蜂群算法[17]进行算法对比,记录每个算法运行10次的结果。某液压件厂实际案例的初始调度甘特图如图2所示,模拟其发生动态扰动,扰动情况如表5所示。算法实验数据如表6所示。

表5 动态扰动详情
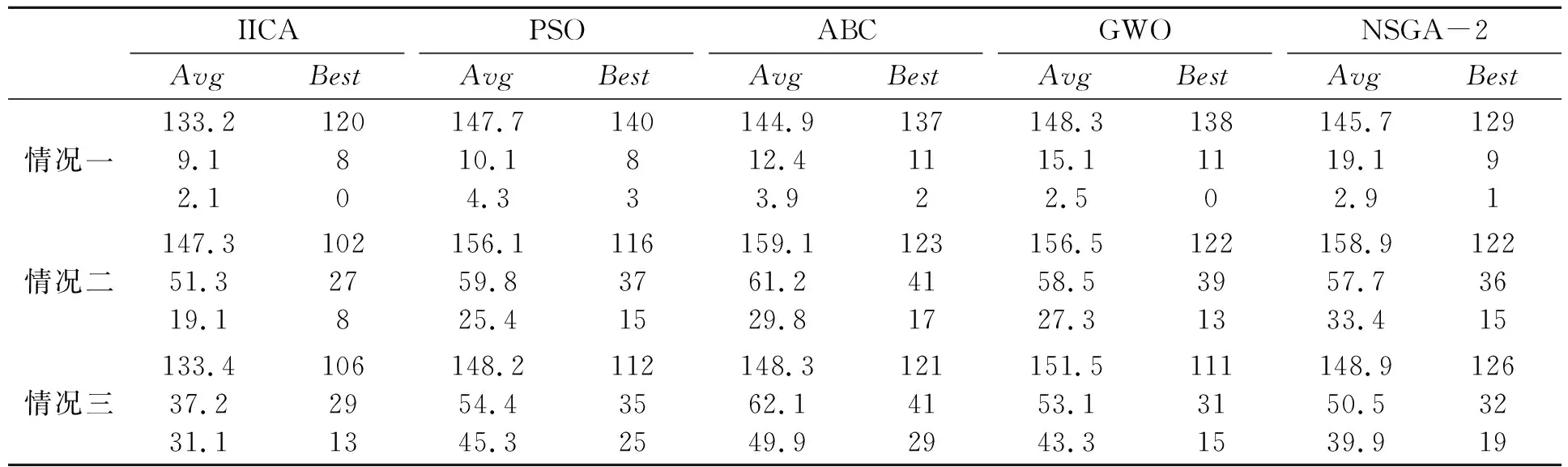
表6 算法实验数据
从表6可知,IICA算法在3种情况下均取得了最优解,证明了改进算法的有效性。以情况三为例,算法最优解情况如图3所示,动态调度后的最优甘特图如图4所示。
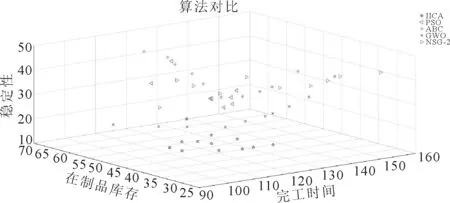
图3 算法最优解对比图

图4 动态调度甘特图
4 结论
研究考虑次品处置的液压缸零部件车间多目标动态调度问题。在模型上,考虑了液压缸装配车间零部件繁多,提出了在制品库存最小为调度目标。在算法上,以ICA算法核心框架为内核,通过引入文化入侵操作、保护最弱帝国的帝国竞争行为,保护了种群多样性避免算法陷入局部最优解。最后通过基准测试算例进行策略对比实验,结果验证了改进算法的有效性。
