基于模糊神经网络控制方法的光伏发电系统并网设计

陈宇能，陈景贤，廖钧濠，陈秀雯

摘 要：针对光伏发电系统运行过程中极易受到环境温度、太阳辐照度等外部条件干扰，从而导致其输出功率存在间歇性、随机性问题的情况，提出一种基于模糊控制算法及前馈（BP）神经网络的智能控制方法（下文简称为“模糊神经网络控制方法”）来进行光伏发电系统并网设计，并搭建并网电路模型进行仿真分析。分析结果显示：相较于扰动观察法、模糊控制算法，采用模糊神经网络控制方法的并网光伏发电系统的泛化能力和鲁棒性更强，能更好地提高系统的稳态性和可靠性，可有效解决光伏发电输出功率存在的间歇性和随机性问题。

关键词：光伏发电系统；最大功率点追踪；神经网络；模糊控制算法；并网

中图分类号：TM615 文献标志码：A

0  引言

随着化石能源过度消耗，环境污染问题日趋严重，开发利用清洁、高效的可再生能源已成为世界各国能源发展的必然趋势[1]。太阳能是一种无噪声、无污染、资源分布不受地域限制的可再生能源，而光伏发电被认为是最有发展前景的太阳能利用方式之一。虽然利用微电网将光伏电力接入配电网能提高配电网的输配电容量[2-3]，但却无法完全解决光伏发电系统输出功率存在波动性、不稳定的问题[4] 。此外，当光伏发电系统受到外部环境干扰而导致其输出电压产生波动时，其并网后电网也会受到相应的扰动，进入“孤岛”运行模式[5]。

目前，国内外关于优化光伏发电系统输出功率分配的研究主要是采用逆变器结合相应的控制手段来提高光伏发电系统并网时的电能质量。比如：文献[6]提出使用动态恒定电压法实时跟踪光伏发电系统的最大功率点（MPP）电压，但该方法需要具备高精度的环境温度、太阳辐照度传感器，增大了硬件成本；文献[7]通过采用扰动观察法对光伏发电系统进行扰动，以改变占空比，从而实现最大功率点追踪，但在最大功率点处仍存在波动；文献[8]提出以粒子群优化（PSO）模糊控制算法追踪光伏发电系统的最大功率点，虽然该方法全局搜索能力强、准确性较高，但易陷入局部最优。

上述文献均是通过光伏发电系统输出特性曲线来追踪最大功率点，并通过算法提高追踪精度，但仍难以解决光伏发电输出的间歇性和随机性问题。本文提出一种基于模糊控制算法及前馈（BP）神经网络的智能控制方法（下文简称为“模糊神经网络控制方法”）来进行光伏发电系统并网设计，该方法利用多层BP神经网络强大的推理能力，直接预测出光伏发电系统最大功率点电压；再通过模糊控制算法，利用专家经验，实时调整占空比，推算出光伏发电系统最大功率点，从而提高系统的泛化能力和鲁棒性，进而有效抑制光伏发电系统输出的间歇性和随机性，为并网光伏发电系统的安全运行提供保障。

1  模型的搭建

1.1  光伏组件的等效电路模型

光伏组件是利用光生伏特效应将太阳能转变为电能的装置。典型的光伏组件等效电路模型可看作是一个受控电流源[9]，具体如图1所示。图中：Rs和Rp分别为光伏组件的等效串联电阻和等效并联电阻；Is和Ip分别为流经光伏组件等效串联电阻和等效并联电阻的电流；Ipc为光生电流；Id为流经二极管的电流；Ipo为光伏组件的输出电流；Vpo为光伏组件的输出电压；D为二极管。

根据基尔霍夫电压定律（KVL）可知，流经光伏组件等效并联电阻的电流可表示为：

（1）

流经二极管的电流可表示为：

（2）

式中：Io为光伏组件的反向饱和电流；q为电荷量常数；Vpv为二极管两端的电压；nc为二极管理想因子；k为玻尔兹曼常数；Tc为光伏组件工作温度。

根据基尔霍夫电流定律（KCL）可知，光伏组件的输出电流可表示为：

Ipo=Is=Ipc–Id–Ip                                                 （3）

将式（1）和式（2）代入式（3），则可得到光伏发电的输出特性方程，即：

（4）

1.2  光伏阵列输出特性

由于单块光伏组件的输出电流过小、输出功率过低，难以实现与市电并网。因此由多块光伏组件按拓扑结构相互连接构成光伏阵列，并将其作为光伏发电的研究对象。单块光伏组件的工作参数如表1所示。

太阳辐照度和环境温度的变化都会对光伏阵列的输出特性造成影响。针对同一个光伏阵列，通过改变这两个因素，研究不同环境温度和不同太阳辐照度下光伏阵列的输出特性。

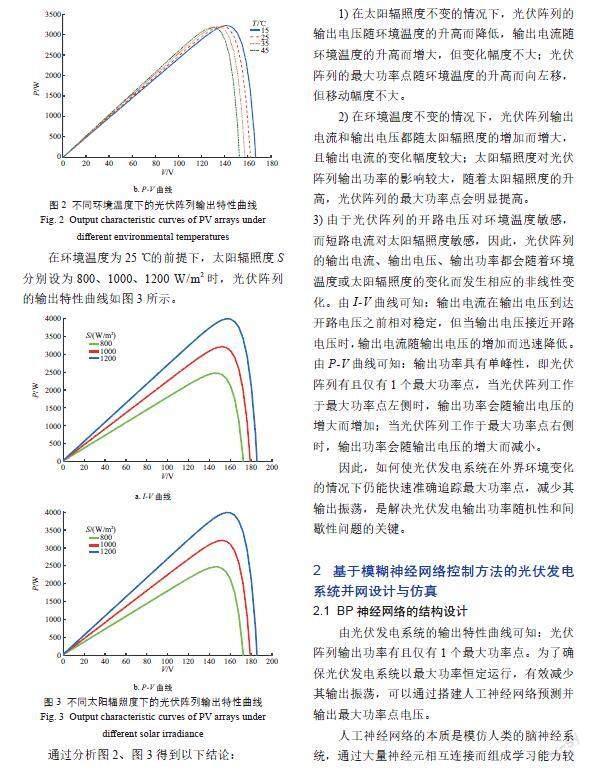
在太阳辐照度为1000 W/m2的前提下，环境温度T分别设为15、25、35、45 ℃时，光伏阵列的输出特性曲线如图2所示。图中：I为光伏阵列的输出电流；V为光伏阵列的输出电压；P为光伏阵列的输出功率。

在环境温度为25 ℃的前提下，太阳辐照度S分别设为800、1000、1200 W/m2时，光伏阵列的输出特性曲线如图3所示。

通过分析图2、图3得到以下結论：

1）在太阳辐照度不变的情况下，光伏阵列的输出电压随环境温度的升高而降低，输出电流随环境温度的升高而增大，但变化幅度不大；光伏阵列的最大功率点随环境温度的升高而向左移，但移动幅度不大。

2）在环境温度不变的情况下，光伏阵列输出电流和输出电压都随太阳辐照度的增加而增大，且输出电流的变化幅度较大；太阳辐照度对光伏阵列输出功率的影响较大，随着太阳辐照度的升高，光伏阵列的最大功率点会明显提高。

3）由于光伏阵列的开路电压对环境温度敏感，而短路电流对太阳辐照度敏感，因此，光伏阵列的输出电流、输出电压、输出功率都会随着环境温度或太阳辐照度的变化而发生相应的非线性变化。由I-V曲线可知：输出电流在输出电压到达开路电压之前相对稳定，但当输出电压接近开路电压时，输出电流随输出电压的增加而迅速降低。由P-V曲线可知：输出功率具有单峰性，即光伏阵列有且仅有1个最大功率点，当光伏阵列工作于最大功率点左侧时，输出功率会随输出电压的增大而增加；当光伏阵列工作于最大功率点右侧时，输出功率会随输出电压的增大而减小。

因此，如何使光伏发电系统在外界环境变化的情况下仍能快速准确追踪最大功率点，减少其输出振荡，是解决光伏发电输出功率随机性和间歇性问题的关键。

2  基于模糊神经网络控制方法的光伏发电系统并网设计与仿真

2.1  BP神经网络的结构设计

由光伏发电系统的输出特性曲线可知：光伏阵列输出功率有且仅有1个最大功率点。为了确保光伏发电系统以最大功率恒定运行，有效减少其输出振荡，可以通过搭建人工神经网络预测并输出最大功率点电压。

人工神经网络的本质是模仿人类的脑神经系统，通过大量神经元相互连接而组成学习能力较强的运算模型。由这些神经元所搭建的网络理论上可以向任意的已知函数学习[10]。本文采用BP神经网络，其利用误差反向传播训练算法，基本原理是梯度下降法，即通过调整权值使神经网络的实际输出值与期望输出值之间误差的均方根值最小[11]。BP神经网络结构图如图4所示。图中：太阳辐照度和环境温度均为输入信号；参考输出电压Vref为输出信号；wij为连接输入层与隐含层之间的权值；wki为连接隐含层与输出层之间的权值。

将输入的环境温度、太阳辐照度数据进行归一化处理，归一化区间为[0，1]。以归一化后的数据作为BP神经网络的二维输入向量，将隐含层神经元个数设置为7，输出层神经元个数设置为1，数据采样的间隔为0.01，设定目标误差为0.0001，学习速率设定为0.01；并用S型正切函数tansig作为隐含层神经元的传递函数，以S型对数函数logsig作为输出层神经元的传递函数，以trainlm函数进行BP神经网络训练。

以某个光伏阵列为例，将其最大功率点下的实际输出电压与BP神经网络预测的参考输出电压进行对比，对比结果如图5所示。

由图5可知：所采用的BP神经网络可在未知光伏阵列相关电气参数的条件下，通过搭建相关模型，将输入的环境温度、太阳辐照度数据归一化、训练、测试，可以较准确地预测最大功率点下的参考输出电压，且神经网络的逼近效果较高，训练误差较小，泛化能力较好，适用于非线性系统。

由此可见，利用BP神经网络来追踪光伏发电系统最大功率点具有很大优势，能够抑制光伏发电系统输出电压的不稳定性，有效解决输出功率的间歇性和随机性问题。

2.2  模糊控制算法跟踪光伏阵列最大功率点

以BP神经网络预测的参考输出电压与光伏阵列实际输出电压的偏差E和偏差的变化量EC作为模糊控制算法的输入信号，判断光伏阵列输出功率点与最大功率点之间的位置关系，通过调节作为输出信号的占空比，使输出电压值趋向峰值电压。将BP神经网络预测的参考输出电压与实际输出电压偏差及偏差变化量的模糊子集设为{NB， NM， NS， ZO， PS， PM， PB}，论域为{-1， 1}。其中：NB、NM、NS、ZO、PS、PM、PB分别为论域中的负大、负中、负小、零、正小、正中、正大。同时均选用含有中等模糊状态定义的三角形作为隶属函数。

第K次采样下BP神经网络预测的参考输出电压Vref（K）和光伏阵列实际输出电压V（K）的偏差E（K）及偏差变化量EC（K）可分别表示为：

E（K）=V（K）–Vref（K）                                        （5）

EC（K）=E（K）–E（K–1）                                      （6）

根據光伏阵列的P-V特性曲线制定4条模糊控制规则，分别为：

1）当EC（K）>0、E（K）>0时，输出功率点在最大功率点左侧，且逐渐远离最大功率点；

2）当EC（K）>0、E（K）<0时，输出功率点在最大功率点右侧，且逐渐靠近最大功率点；

3）当EC（K）<0、E（K）>0时，输出功率点在最大功率点左侧，且逐渐靠近最大功率点；

4）当EC（K）<0、E（K）<0时，输出功率点在最大功率点右侧，且逐渐远离最大功率点。

确定模糊控制规则后，可得到输出功率变化时的占空比，并可制定出相应的模糊控制规则表，具体如表2所示。

在不影响跟踪速度的前提下，将清晰化的最大功率点电压与三角波进行调制，采用MAX-MIN推理方法调控步长。步长大小随输出功率点与最大功率点的距离自动调整，方向与输出功率增加的方向相同。通过调节开关管的占空比进而改变光伏阵列的输出电压，跟踪最大功率点，实现最大功率输出。

2.3  光伏输出的仿真与分析

神经网络通过学习、训练得到的自适应样本数据，可直接预测出最大功率点电压，其具有非线性适应性信息处理能力，但需大量数据才能提高神经网络的泛化能力；而且通常情况下，神经网络欠缺规则表达能力且会出现过拟合现象。而模糊控制算法易于利用专家经验，能够表达和处理难以求取的信息，但模糊规则的提取缺乏学习能力[12]。由此可见，神经网络和模糊控制算法具有互补特性。因此，可采用神经网络和模糊控制算法相结合的方式跟踪光伏发电系统的最大功率点电压。

采用模糊神经网络控制方法的并网光伏发电系统示意图如图6所示，图中：L为Boost升压电路的电感；De为Boost升压电路的二极管；Co为输出的滤波电容；Cpv为输入的滤波电容；O为功率开关管。

该控制方法的工作原理为：首先将环境温度和太阳辐照度的相关数据输入到BP 神经网络中，归一化后訓练测试数据，通过调整BP神经网络权值使光伏阵列的输出电压不断逼近期望的最大功率点电压；将BP神经网络预测的参考输出电压与光伏阵列实际输出电压的偏差输入到模糊控制器中，再通过模糊逻辑算法实时调节占空比，追踪最大功率点，并通过并网模型将光伏发电系统的电力输送到电网中，供电网调度。

假设光伏发电系统处于标准测试条件（太阳辐照度为1000 W/m2、环境温度为25℃、AM1.5）下，不考虑光伏组件阴影遮挡问题，且光伏发电系统的最大功率为3200 W，为了验证最大功率点追踪（MPPT）算法的正确性，在光伏发电系统运行时间t为0.3 s时将太阳辐照度由1000 W/m2突变为800 W/m2，环境温度保持不变，仿真时采用变步长ode23tb算法，对比扰动观察法、模糊控制算法、模糊神经网络控制方法的跟踪效果，具体如图7所示。

由图7可以看出：3种方法均可跟踪最大功率点。扰动观察法的跟踪效果一般，在0.08 s后才趋于稳定，且其对于太阳辐照度的突变，重新跟踪的速度较慢，响应时间较长，振幅较大，存在最大功率点振荡和误判等缺点。相较于扰动观察法，模糊控制算法的波形更加平滑，稳态时的振荡更轻微，且输出功率在0.05 s后基本稳定；同时，该方法跟踪到的光伏发电系统最大功率约为2943 W，跟踪性能参数Km=2943 W/3200 W=0.919，跟踪性能较好。在t=0.3 s后，模糊控制算法能够快速进行重新跟踪，动态过渡时间和响应时间都较短。由此可见，模糊控制算法能使光伏发电系统输出功率波形得到明显改善，有效降低输出的不稳定性。

相比于扰动观察法和模糊控制算法，采用模糊神经网络控制方法的光伏发电系统的输出功率在0.03 s基本稳定，达到最大功率点后基本无振荡，最大功率约为3038 W，跟踪性能参数为0.949，跟踪性能最好，稳态性能也更好；且在t=0.3 s时的扰动作用下能快速准确判定最大功率点走向，抗干扰能力强，无误判现象。由此可知，BP神经网络与模糊控制相结合，能更好学习与推理，快速预测和追踪最大功率，更好解决光伏发电输出的间歇性和随机性，提高光伏发电系统稳定性。

3  光伏发电系统并网分析

为了将光伏发电系统的输出功率安全送到电网，供电网调度，需通过逆变器进行控制，以便于与市电同步，满足并网条件。逆变器根据直流侧电源性质可以分为两大类：电流型逆变器和电压型逆变器。由于电流型逆变器需在输出侧串联大电感，以稳定输入电流，考虑到实际装置的体积和电路动态过程，最后采用电压型逆变器，搭建全桥逆变型电路，并采用LCL型滤波器和电流滞环比较器。

LCL型滤波器虽然可以抑制高频段信号，但高频谐波分量被放大，若谐波直接流入电网，不利于电网的安全运行。为了改变LCL型滤波器的幅频特性，减少输出畸变，抑制谐振，故在LCL型滤波器电容中串联阻尼电阻[13]。本文搭建的并网电路模型如图8所示。图中：i、iref分别为光伏发电系统的输出电流和参考输出电流；L1、L2均为电感；C为电容；R为电阻。

为了减少谐波分量，提高逆变器的电流输出精度，电流滞环比较器1和电流滞环比较器2的滞环宽度分别为-0.65～0.70 A和-0.70～0.65 A，且留有“死区时间”，避免逆变桥直通。本文搭建的并网电路模型的相关参数如表3所示。

考虑到光伏发电系统的实际并网情况，逆变器与电网之间应接入变比为1：2的工频隔离变压器，以保护直流回路，避免谐波流入电网[14]。为测试电流滞环比较器的跟踪效果，在工作频率为50 Hz的情况下，对并网光伏发电系统进行运行仿真，得到给定电流和跟踪电流的波形图，如图9所示。

从图9可看出：给定电流的幅值为20 A，跟踪电流从0. 02 s后与给定电流的幅值和相位基本保持一致。

从0.05～0.35 s时间段内的跟踪电流中选取15个周波进行傅里叶变换，得到电流滞环比较器跟踪电流的谐波分量和不含基波的谐波分量，结果如图10所示。

从图10可看出：电流滞环比较器跟踪电流的谐波分量幅值为19.91 A，十分接近20 A，可近似看成其占给定电流的比例接近100%；不含基波的

谐波分量占比基本为零；总谐波失真为3.26%，符合电气与电子工程师协会（IEEE）对并网光伏发电系统输出电流总谐波失真不超过5%的要求。除去基波的谐波分量后，偶次谐波分量占跟踪电流谐波的比例较小，可忽略不计；电流谐波含量最高的是三次谐波，所占比例不到0.1%，五次谐波分量所占的比例不到0.03%，且高次谐波总占比不到0.05%。由此可看出：并网光伏发电系统的运行效果较好，采用模糊神经网络控制方法能有效改善谐波输出，提高电能质量，避免谐波直接入网，从而提高电网运行效率。

4  结论

本文提出了一种基于模糊神经网络控制方法来进行光伏发电系统并网设计的方法，并利用该方法对并网光伏发电系统进行了仿真分析。分析结果显示：相较于扰动观察法、模糊控制算法，采用模糊神经网络控制方法的并网光伏发电系统的泛化能力和鲁棒性更强，能更好地提高系统稳态性和可靠性，有效解决了光伏发电输出功率存在的间歇性和随机性问题。此外，采用双电流滞环比较器后，并网光伏发电系统输出电流的高次谐波分量小，电流滞环比较器的跟踪精度较高，更有效提高了电能质量和保障了电网的安全运行。

[参考文献]

[1] 李凡双，王展旭. 基于Cuk电路的光伏MPPT模糊控制系统仿真研究[J]. 自动化与仪器仪表，2019（4）：103-105，109.

[2] 张耀月.并网模式下的风光混合微电网中可再生分布式电源的建模与仿真[J].科技经济导刊，2018，26（35）：34-42.

[3] MISHRA S，BORDIN C，TOMASGARD A，et al. A multi-agent system approach for optimal microgrid expansion planning under uncertainty[J]. International journal of electrical power & energy systems，2019，109：696-709.

[4] MAGDY G，SHABIB G，ELBASET A A，et al. Renewable power systems dynamic security using a new coordination of frequency control strategy based on virtual synchronous generator and digital frequency protection[J]. International journal of electrical power & energy systems，2019，109：351-368.

[5] 朱然，孙冀. 国外智能电网技术发展实践综述[J]. 电子质量，2016（9）：24-29.

[6] 倪雨. 基于阻增量光伏动态模型的高精度恒压法设计[J]. 成都信息工程大学学报，2016，31（3）：297-300.

[7] 艾永乐，刘群峰，韩朝阳，等. 基于改进扰动观察法的光伏MPPT策略[J]. 武汉大学学报（工学版），2020，53（4）：339-344.

[8] 徐偲吉吉，查晓锐.基于改进粒子群优化模糊控制的MPPT算法研究[J].电机与控制应用，2019，46（10）：35-39.

[9] BAI W L，LEE K. Distributed generation system control strategies in microgrid operation[J]. IFAC proceedings volumes，2014，47（3）：11938-11943.

[10] 郦丁浩. 基于人工神经网络的MPPT算法研究[D]. 杭州： 浙江工业大学，2018.

[11] 苏海滨，卞晶晶，刘强，等. 基于神经网络的光伏发电最大功率点跟踪算法[J]. 华北水利水电学院学报，2010，31（6）：80-83.

[12] 焦科名，徐凱. 基于神经网络和模糊控制的光伏发电MPPT研究[J]. 计算机仿真，2020，37（5）：71-76.

[13] GOMES C C，CUPERTINO A F，PEREIRA H A. Damping techniques for grid-connected voltage source converters based on LCL filter：an overview[J]. Renewable and sustainable energy reviews，2018，81：116-135.

[14] 李建华. 光伏发电系统并网控制策略研究[D]. 兰州：兰州理工大学，2018.

Grid connection design of PV power generation system based on fuzzy neural network control method

Chen Yuneng1，Chen Jingxian1，Liao junhao1，Chen xiuwen2

（1. College of electronics and information engineering，Guangdong Ocean University，Zhanjiang 524088，China；

2. School of management，Guangdong Nanfang Institute of Technology，Jiangmen 529000，China）

Abstract：In response to the fact that PV power generation systems are highly susceptible to external conditions such as environmental temperature and solar irradiance during operation，resulting in intermittent and random issues with its output power，this paper proposes an intelligent control method based on fuzzy control algorithm and BP neural network （hereinafter referred to as“fuzzy neural network control method”） for grid connection design of PV power generation systems，and builds a grid connection circuit model for simulation analysis. The analysis results show that compared to the disturbance observation method and fuzzy control algorithm，the fuzzy neural network control method used in the grid connected PV power generation system has stronger generalization ability and robustness，which can better improve the steady-state and reliability of the system，and effectively solve the intermittent and random problems in the output power of PV power generation.

Keywords：PV power generation system；MPPT；neural network；fuzzy control algorithm；grid connection