底轴驱动翻板闸门底轴计算方法探讨

张 辉，杨春娟

（中水北方勘测设计研究有限责任公司，天津 300222）

底轴作为底轴驱动翻板闸门荷载传递和门叶支撑的关键构件，直接影响到闸门的安全，并对工程造价具有较大影响，底轴的设计是该类型闸门设计的关键。由于底轴驱动翻板闸门应用时间尚短，底轴受力复杂，目前无该型闸门计算的行业规范。本文以新乡某工程底轴驱动翻板闸门为例，对其底轴进行理论计算，并通过有限元仿真进行验证，为底轴驱动翻板闸门的设计提供参考。

1 闸门基本参数

闸门设计参数为32.8 m×4.5 m-4.8 m（宽×高-挡水水头），挡水工况下门顶溢流0.3 m。闸门门叶厚度600 mm。闸门为主纵梁结构，共设主纵梁20 根，其间距约1640 mm。闸门在高度方向上设横向次梁6 根，其间距约750 mm。底轴直径1200 mm，最大壁厚60 mm，每扇闸门在闸室内设置5 个支铰。闸门常闭，维持上游侧常水位。闸门动水启闭、非汛期启闭时，水位预降至闸上3.5 m 水头；汛期操作时，水位预降至闸上2 m 水头。闸门启闭机容量2×2500 kN。闸门总图，如图1 所示。

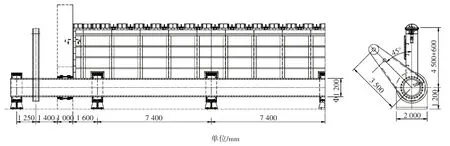
图1 闸门总图

2 底轴理论计算

底轴驱动翻板闸门动水启闭，作用在闸门上的动水压力包括时均压力和脉动压力两部分[1]。闸门的运行方式和泄流过程与舌瓣闸门类似，运行时闸门绕底轴旋转，闸门面板上部过流。根据舌瓣门水力学经验公式，闸门最大动水压力发生在门叶与底板呈0～40°范围内，闸门荷载呈梯形分布，作用在门叶上的水压力荷载分布如图2所示。

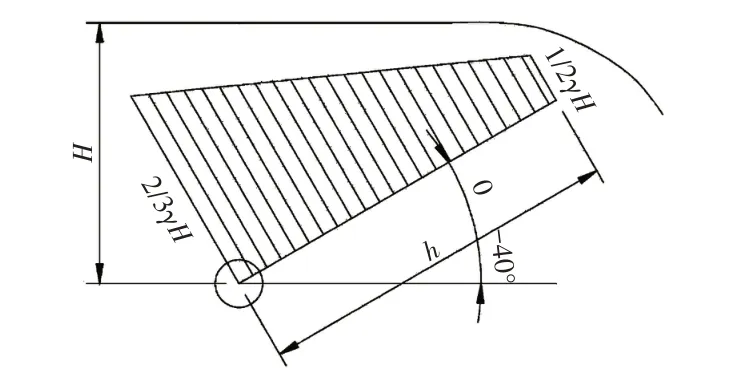
图2 门叶宽度方向的动水压力分布

作用在闸门底轴上的主要荷载有启闭力、水压力、闸门自重和支铰反力。底轴受弯矩、扭矩和剪力的综合作用，受力情况复杂。

在上述荷载中，支铰摩擦力较小，计算时未计入。因此，底轴计算模型可等效为启闭力、水压力和自重作用下的弯扭组合模型。根据剪切胡克定律，圆轴扭转变形前原为平面的横截面变形后仍保持为平面，形状和大小不变，相邻两截面间的距离不变[2]。根据底轴扭转平面假设理论，扭转变形中底轴横截面如刚性平面，绕轴线旋转一定角度。由于底轴同时承受沿轴方向的弯矩，弯曲变形与扭转变形垂直，不会影响底轴的扭转。

进行弯矩计算时，底轴可视为支承在支铰上的多跨连续梁，由水压力和闸门自重作用在底轴的弯矩和抗弯截面模量对比，能够发现底轴弯矩对底轴强度和刚度影响较小。

根据上述分析，得出以下结论：闸门底轴的计算主要为均布扭转力矩作用下轴的扭转计算。本文重点探讨底轴扭转变形的理论计算方法。在现实情况中，门叶结构对底轴的抗扭具有有利影响，但难以采用理论方法准确计算。由于门叶的抗扭截面模量与底轴的抗扭截面模量相比，对计算结果的准确性影响较小，从计算的简便性和使用的安全性出发，本计算中未考虑门叶刚度对底轴的影响。闸门门叶结构对底轴抗扭的具体影响通过有限元分析进行验证。

2.1 闸门运行工况下水压力产生的底轴扭转角度计算

根据前述结论，参照轴的扭转计算模型，闸门运行工况下由水压力产生的底轴扭转角度计算公式如下：

式中：φs为水压力产生的底轴扭转角度（rad）；ms为水压力作用在底轴单位长度上的扭转力矩（kN·m/m）；ps为闸门单位长度上的荷载（kN/m）；γ为水容重（kN/m3），取10 kN/m3；z为作用在闸门底轴上的水压力力臂长度（m），取2.85 m；H为设计水头（m），取4.8 m；h为门叶高度（m），取4.5 m；d为底轴外径（m），取1.2 m；G为材料的切变模量（kPa），取7.9×106kPa；Ip为底轴的极惯性矩（m4），取7×10-2m4；x为水压力沿底轴的积分长度（m）。

经计算，得闸门运行工况下水压力产生的底轴扭转角度φs= 0.01128 rad。

2.2 闸门运行工况下门叶重量产生的底轴扭转角度计算

闸门重量对底轴的影响与水压力相似，为均布扭转力矩作用下轴的扭转计算，其计算公式如下：

式中：φg为闸门自重产生的底轴扭转角度（rad）；mg为门叶重力作用在底轴单位长度上的扭转力矩（kN·m/m），取0.0126 kN·m/m；其余变量含义同上。

经计算，得闸门运行工况下门叶重量产生的底轴扭转角度φg= 3.43×10-4rad。

2.3 闸门挡水工况下底轴扭转角度计算

在闸门关闭挡水工况下，闸门重心基本与底轴轴线重合，此时不考虑闸门自重产生的扭转力矩影响。由水压力产生的底轴扭转角度计算公式如下：

式中：φd为挡水工况时水压力产生的底轴扭转角度（rad）；md为水压力作用在底轴单位长度上的扭转力矩（kN·m/m），取0.241kN·m/m;pd为作用在闸门单位长度上的水压力（kN/m），取114.75 kN/m；其余变量含义同上。

经计算，得闸门挡水工况下底轴扭转角度φd=0.0079 rad。

根据计算结果，闸门底轴在闸门对称中心处变形最大，最大扭转变形量为φ=φs+φg=0.01162 rad。由底轴扭转造成的闸门门叶变形为f=(φd+φg)(d/2 +h)= 59.3 mm。闸门挡水时闸门底轴扭转变形量为φ=φd= 0.0079 rad，由底轴扭转造成的闸门门叶变形为fd=φd(d/2 +h) = 40.3 mm。

3 有限元验证

3.1 有限元模型构建

为验证理论计算结果，利用ANSYS 构建有限元模型。ANSYS 单元中SHELL181单元既具有弯曲能力又具有膜力，可以承受平面内荷载和法向荷载，非常适用于线性分析及大转动、大变形的非线性分析[3,4]，因此闸门主要构件采用SHELL181单元。

本工程底轴驱动翻板闸门为两侧驱动，模型为沿孔口中心线的对称结构，为提高模型计算速度，有限元模型构建1/2结构，如图3所示。

图3 底轴驱动翻板闸门有限元模型

3.2 有限元模型约束施加

在模型上施加梯形单元荷载，根据图2水力学模型，门顶水压强为2.4 kPa，门叶底部水压强为3.2 kPa，门叶荷载分布如图4 所示。闸门运行时，启闭机驱动底轴转动，支铰对底轴的约束为除底轴沿轴线方向的转动外其余5个方向的位移。启闭机对拐臂的荷载通过对拐臂轴孔施加大小、方向与启闭力相同的集中荷载来模拟。在闸门挡水工况下，锁定装置将拐臂锁定。为模拟这一约束状态，对拐臂轴孔施加全部约束。

图4 门叶荷载分布

3.3 应力应变云图分析

运行工况下，闸门变形云图如图5所示，闸门最大变形发生在孔口中心线位置的门叶顶端，闸门变形为63.846 mm。该工况下闸门底轴的扭转变形云图如图6 所示，闸门底轴最大扭转角度为0.011216 rad，发生在门叶中心线位置。该工况下闸门门叶变形和底轴扭转变形的理论计算结果为59.3 mm 和0.01162 rad。挡水工况下闸门变形云图如图7 所示，该工况下闸门最大变形趋势与运行工况相同，最大变形量为40.3865 mm。挡水工况下底轴扭转变形云图如图8 所示，最大扭转变形发生在孔口中心位置，最大扭转变形量为0.00708 rad。挡水工况下相应的理论计算结果分别为40.3 mm和0.0079 rad。

图5 运行工况下闸门变形云图

图6 运行工况下底轴扭转变形云图

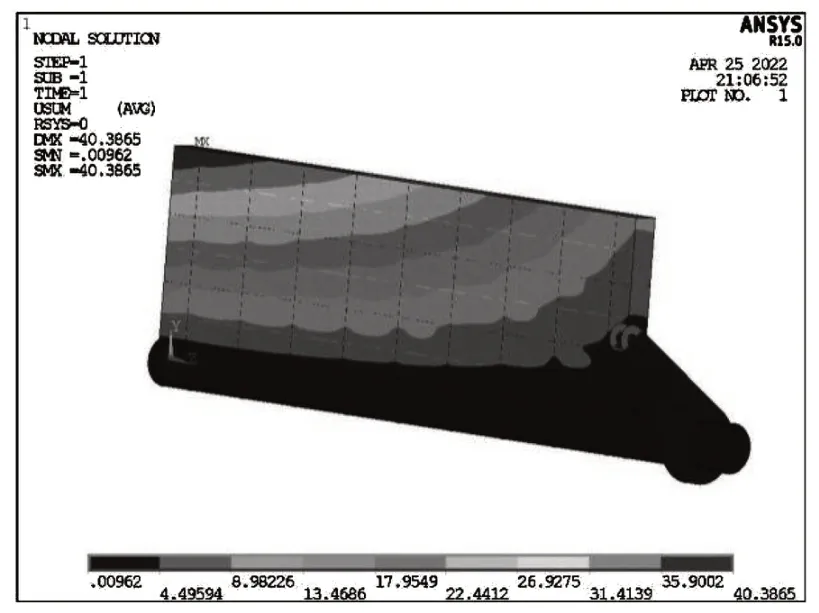
图7 挡水工况下闸门变形云图

图8 挡水工况下底轴扭转变形云图

根据应变云图反映，有限元模型应变和应力变形趋势符合实际情况。通过有限元分析结果和理论计算结果对比可以得出以下结论：①理论计算与有限元分析结果吻合，说明该理论计算方法可行；②理论计算时，底轴的扭转角度稍大，是因为理论计算忽略了闸门门叶结构的有利影响；③闸门门叶变形对比时，理论计算较有限元分析稍小，是因为理论计算时忽略了主纵梁自身在荷载作用下的变形，但两者结果差距不大。

4 结语

通过对比分析理论计算结果与有限元仿真结果，可以得出以下结论。

（1）底轴驱动翻板闸门底轴采用轴的弯扭组合计算是正确的。

（2）门叶结构对底轴抗扭影响较小，其有利影响可作为底轴的安全储备。

（3）将底轴计算简化为均布水压力下的扭转问题基本上不影响计算结果的准确性，适用于闸门可行性研究和初步设计阶段的快速简化计算，可在不影响准确性的情况下节约大量时间。