基于小波-LSTM的流溪河流域短期库水位预测模型

2023-12-06张浩森康爱卿

海河水利 2023年11期

张浩森，龙岩，康爱卿

（1.河北工程大学水利水电学院，河北邯郸 056038；2.河北工程大学河北省智慧水利重点实验室，河北邯郸 056038；3.中国水利水电科学研究院，北京 100038）

1 引言

水库水位预报是防汛抗洪和水库调度的基础，高效精准的库水位预测对水库调度决策、降低灾害风险具有重要意义[1]。然而，水库水位变化受降雨量等诸多因素影响，水库水文序列数据通常表现出显著的时序性、复杂性和波动性等特征[2]，尤其是近些年气象复杂多变，局部灾害性天气事件频发，多流域洪水存在并发重发现象，水库水位的快速变化也呈现增多趋势，这使得库水位预测面临巨大的挑战。

目前，对于库水位预测的研究方法主要分为基于物理过程的水动力模型[3]和基于大数据的数据驱动模型[4]。水动力模型的精细化建模可以实现水位过程的精确模拟，其模拟精度也是当下最高的，但是水动力模型对地形等基础数据要求较高，且存在计算资源消耗高、计算效率低等问题[5，6]。因而，研究采用基于大数据的数据驱动模型开展流溪河流域库水位的短期预测。相较于传统模型，数据驱动模型可以更有效地利用时序数据的时变特性[5]。其中，LSTM（长短时记忆神经网络）模型利用自身的门控结构和细胞单元，解决了传统ANN（人工神经网络）在处理长序列数据时面临的梯度消失或爆炸问题，对于长序列数据具备更好的预测效果，在水文长序列预测中已得到广泛应用[7-11]。然而，基于小波-LSTM 模型的库水位预测研究较少，因此，本文以流溪河流域的流溪河水库和黄龙带水库为研究对象，构建了基于小波-LSTM 的流溪河流域短期库水位预测模型，对不同预见期和不同输入特征下的库水位进行了对比分析，旨在为水库水位预测提供参考。

2 研究区及数据

2.1 研究区概况

流溪河位于广东省广州市东北、北江和东江之间，干流全长约157 km，流域（113°10′12″E～114°2′00″E，23°12′30″ N～23°57′36″ N）总面积约2296 km2，年降雨量约1823.6 mm。降雨是流溪河流域水资源的主要来源，84%的降雨集中在汛期（4—9 月），因此流溪河流域降雨具有较强的季节性，且具有降雨强度大、范围广、暴雨频繁等特点[12，13]。

流溪河流域建有完善的雨水情一体化监测体系，共有48 个主要的水库监测站点和123 个雨量监测站点。综合考虑流溪河流域内原始监测数据收集情况，选取流域内部的流溪河水库和黄龙带水库为研究对象，研究区位置及监测站点分布如图1所示。

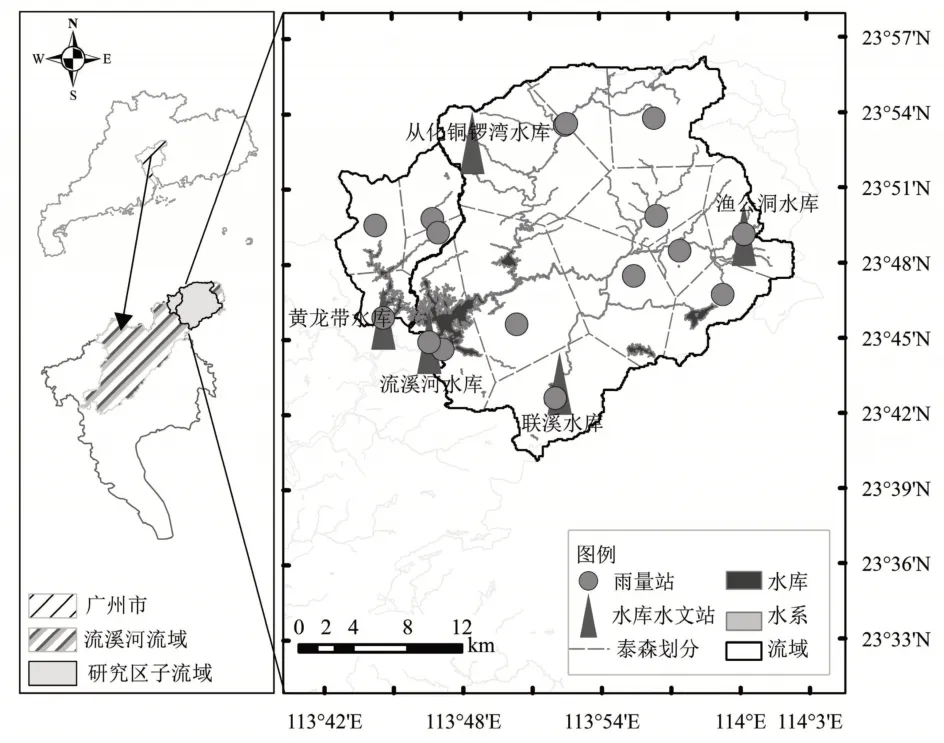
图1 研究区位置示意

2.2 研究数据

研究采用ArcGIS 软件进行子流域划分和雨量站权重确定，并基于收集到的雨量站数据计算子流域面雨量。流溪河水库和黄龙带水库雨量站权重，详见表1。研究收集到的雨量、水位时序数据长度为2015年1 月1 日—2021年1月1日，时序间隔为1 h，序列数据以2019年8 月1 日为界进行数据集划分。

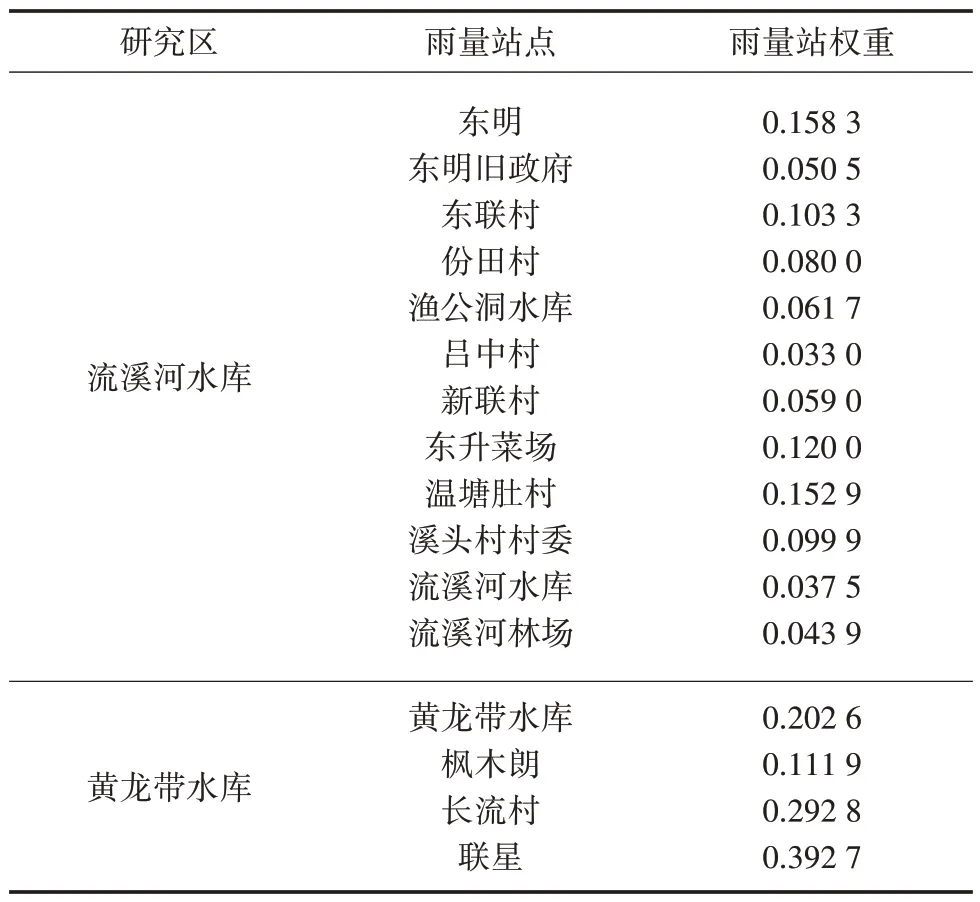
表1 研究区雨量站权重

3 研究方法

3.1 小波分解

小波分解是一种将数据转换到同时带有时域和频域特征的方法，可以实现对时序数据的多尺度细化，达到高频处时间细分、低频处频率细分。这种分解方式增强了局部信号的表现能力，提高了模型的抗噪性[9]，在一定程度上能提升模型精度。小波分解的具体实现可依据参考文献[9]。

本研究采用离散小波对时序数据进行分解处理。考虑到db5小波更适用于分解比较光滑的连续数据集[9]，而经过数据清洗后的水位时序数据总体呈现光滑状态。因而，研究采用db5 小波对流溪河水库和黄龙带水库水位时序数据进行3 阶分解，结果如图2 所示。图2 中S为原始水位时序数据，A3为db5 小波3 阶分解后的低频近似部分，D1、D2和D3为db5小波3阶分解后的高频细节部分。

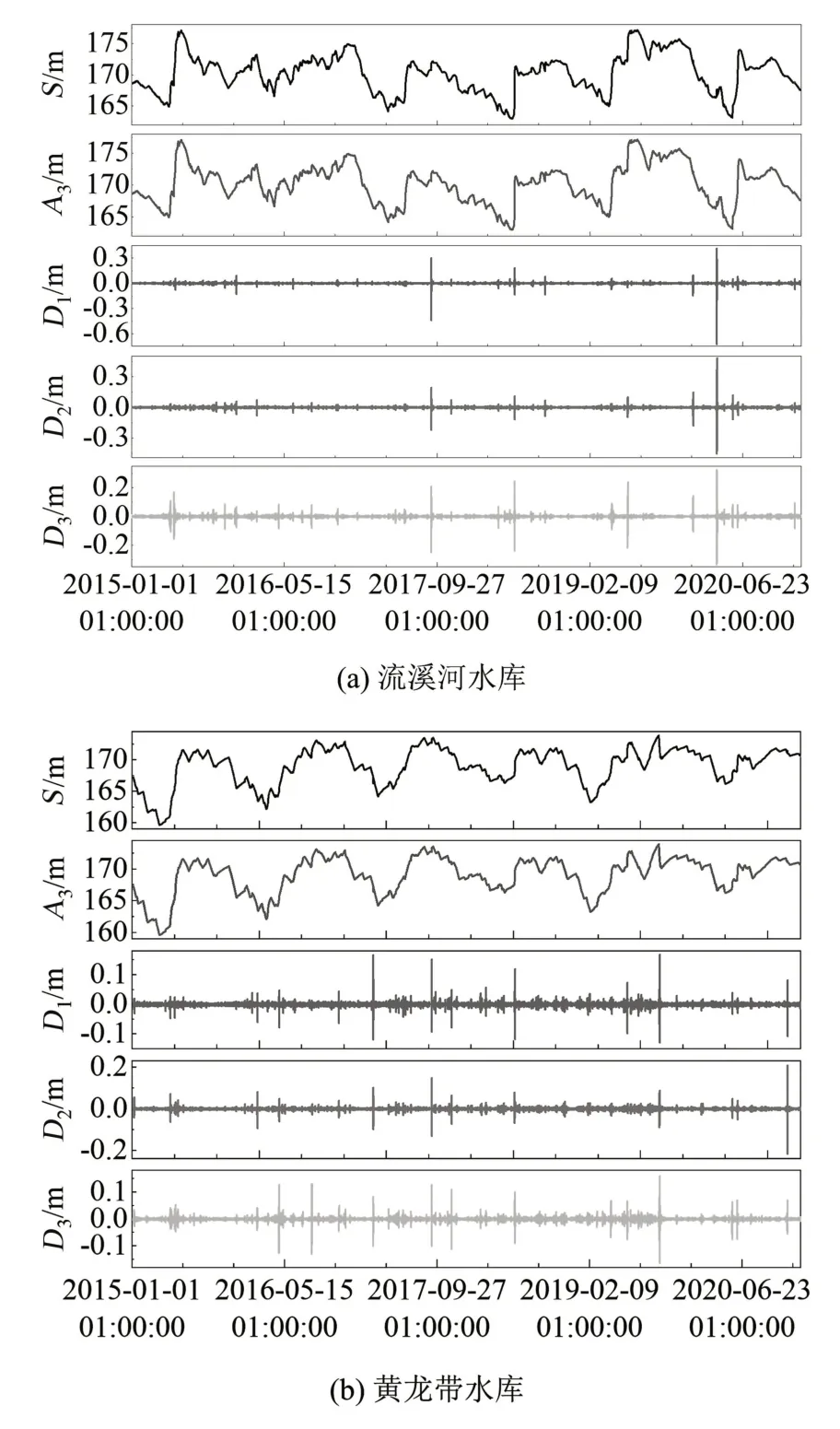
图2 流溪河和黄龙带水库db5小波3阶分解结果

3.2 LSTM模型

RNN（循环神经网络）是用于时序数据分析的特殊神经网络。然而，RNN 在时间步较长时会出现梯度消失现象，在状态权重的模小于1 且时间步较短时梯度会出现爆炸现象，即RNN 对于短期依赖远大于长期依赖，这使得RNN 难以处理长序列时间数据的预测。基于上述问题，LSTM（长短时记忆神经网络）模型应运而生。LSTM 是一种引入门控单元和记忆细胞的特殊形式的RNN，LSTM 模型结构如图3 所示。从图3 可以看出，LSTM 模型通过门控结构和细胞单元控制传输状态，即遗忘门（ft）决定了上一时刻单元状态的保留程度，输入门（it）决定了当前时刻网络的输入有多少可以保存到单元状态，输出门（Ot）则控制单元状态，决定短期记忆流的呈现程度。这种特殊的结构解决了RNN中长期依赖问题，可以更有效地利用时序数据的时变特性。LSTM 模型的具体内部实现可依据参考文献[6]。

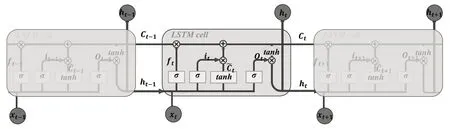
图3 LSTM 模型结构示意

4 预测模型

4.1 数据预处理

模型构建前需对输入数据进行数据清洗和数据变换[14，15]。数据清洗主要是时序数据的异常检测和缺失插补。考虑到原始数据中的异常值大多为突增和突降异常，采用Adtk 异常检测包中的LevelShift-AD突增突降检测算法进行异常检测，并对检测出的异常值采取直接剔除处理。对于经过处理后的时序数据，采用随机森林[16]的方式进行缺失插补。数据变换则是消除模型不同输入特征数据间的差异，便于模型对输入数据进行加权处理，对输出数据进行对比分析。采用z-score 算法对数据进行标准化处理[14]，计算公式为：

式中：x为标准化后的序列数据；xo为原始序列数据；为序列均值；σ为序列标准差。

4.2 模型构建

本研究基于Tensorflow2.0、Python3.8 和Pycharm软件进行水位预测模型构建。为研究小波-LSTM模型的预测精度，分别构建了基于单特征的流溪河水库和黄龙带水库小波-LSTM 模型以及LSTM 对照模型。此外，考虑到流溪河水库水位不仅受子流域面雨量影响，同时还受上游其余水库站点影响，因而，为研究不同输入特征对模型的影响，本研究以流溪河水库为例，构建了流溪河多特征小波-LSTM 模型。其中，单特征是指模型仅以面雨量为输入特征，多特征是指模型以面雨量和流溪河水库站（黄龙带水库站）上游水库水位站点的前期水位为输入特征，单特征和多特征的预测项均是流溪河水库站（黄龙带水库站）未来不同预见期下的水位。

基于上述模型框架，设置模型的输出步长分别为1、6 和12 h，输入步长分别为12、36 和72 h，以均方根误差为损失函数，优化器选取Adam，模型中的网络隐藏层单元数、学习率、每次运行样本数和迭代次数由Python中的Hyperopt库进行优化取值。

4.3 模型评价指标

纳什效率系数（NSE）通常用于量化模型的预测精度，是一个无量纲的精度评估指标；平均绝对误差（MAE）是一个存在量纲的模型精度评估指标，体现的是模型预测和实测数据之间的真实误差，能有效地反映出预测结果的准确度；均方根误差（RMSE）对模型预测数据中的异常值表现更为敏感，也是一个存在量纲的评估指标。在指标实际衡量过程中，RMSE的值越小则表征模型预测和实测数据之间的最大误差越小，模型预测相对越准确。

综上，为量化模型预测精度，使用NSE、MAE和RMSE3种量化指标，计算公式为：

式中：NSE为纳什效率系数；MAE为平均绝对误差（m）；RMSE为均方根误差（m）；ŷi为模拟数据（m）；yi为监测数据（m）；-y为监测数据均值（m）；N为样本总数。

5 结果与分析

5.1 小波-LSTM模型预测结果评估

基于上述3种量化指标，小波-LSTM模型和LSTM模型对流溪河水库和黄龙带水库测试集的预测结果详见表2，模型预测与实测水位对比如图4所示。

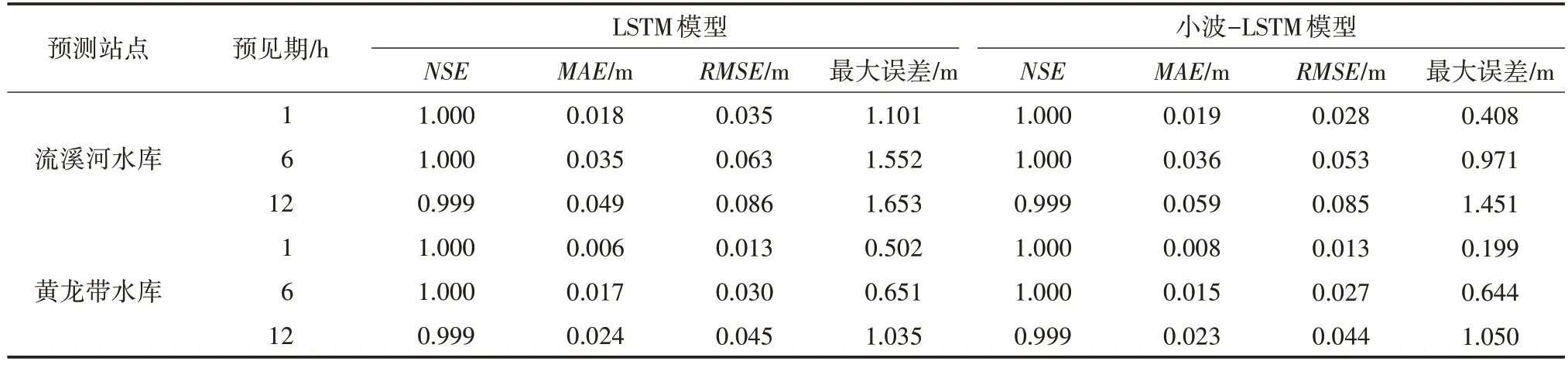
表2 模型测试集预测结果

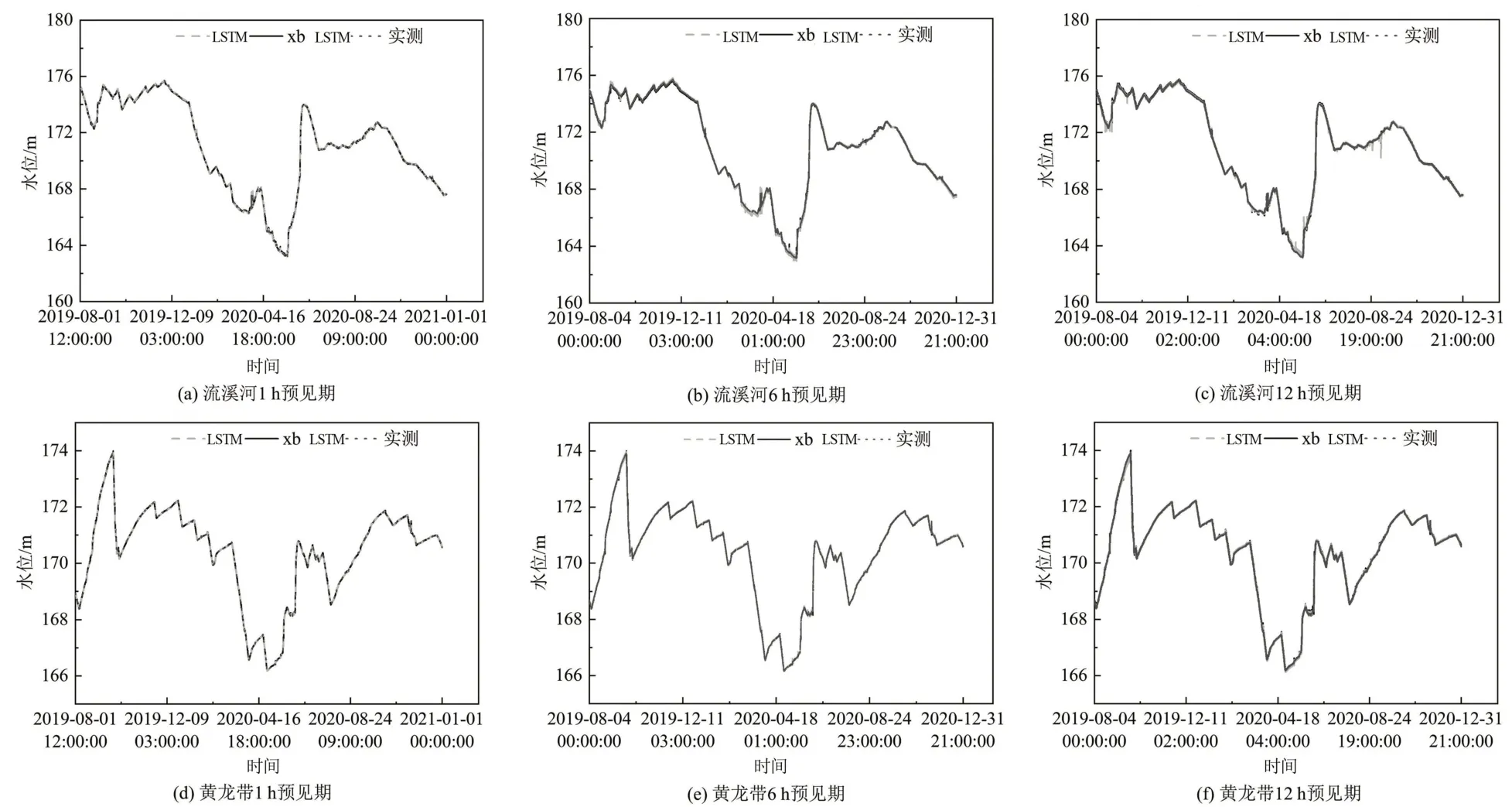
图4 模型预测与实测水位对比

由表2和图4可见：①随预见期的增加，LSTM模型和小波-LSTM 模型的NSE均呈下降趋势，MAE、RMSE和最大误差均呈上升趋势，但流溪河水库和黄龙带水库的NSE均大于0.9，MAE和RMSE均保持在0.10 m 以下。结果表明，2 种模型对于流溪河水库和黄龙带水库均具有很高的可信度，同时均取得不错的预测效果。②就相同预见期而言，小波-LSTM 模型的NSE和LSTM 相差无几，但小波-LSTM模型对应的RMSE和最大误差大多都低于LSTM 模型。以1 h 预见期为例，流溪河水库的LSTM模型的最大误差超出小波-LSTM模型0.693 m，黄龙带水库的LSTM 模型的最大误差超出小波-LSTM 模型0.303 m。结果表明，相同预见期下，小波-LSTM 模型预测的整体误差和极值误差均要优于LSTM 模型，模型的整体预测效果更优。

5.2 不同输入特征情境下模型预测结果评估

以流溪河水库为研究对象，小波-LSTM 模型在1、6 和12 h预见期下的模型预测结果详见表3，模型评价指标对比如图5所示。

表3 模型训练集预测结果

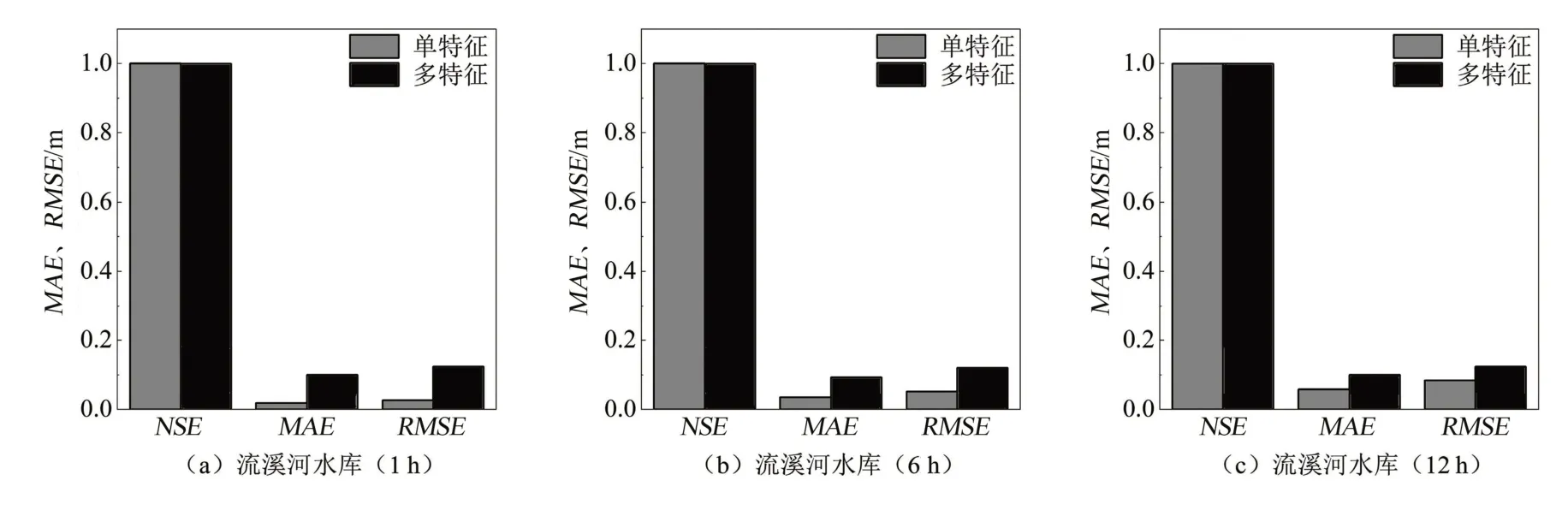
图5 不同输入特征下评价指标对比

由表3 和图5 可见，就NSE而言，单特征小波-LSTM 模型和多特征小波-LSTM 模型相差无几；就MAE和RMSE而言，单特征小波-LSTM 模型在1 h预见期下的最低值分别为0.019和0.028 m，在6 h预见期下的最低值分别为0.036 和0.053 m，在12 h 预见期下的最低值分别为0.059 和0.085 m；就最大误差而言，单特征小波-LSTM 模型的最大误差在1 h 预见期下要低于多特征模型，在6 和12 h 预见期下两者则相差无几。由此可见：①单特征小波-LSTM 模型对水位时序数据的整体预测误差要低于多特征小波-LSTM 模型，对于水位时序数据的整体预测效果更好；②单特征小波-LSTM 模型的极值误差要普遍低于多特征小波-LSTM 模型，即单特征小波-LSTM 模型对水位时序数据预测中的异常值相对少于多特征模型，单特征模型的最大预测误差范围要小于多特征模型，对水位时序数据极值的预测效果相对较优。