风光水储多能互补系统建模与仿真

何立新，陈家亮，雷晓辉，李志会

（1.河北工程大学水利水电学院，河北 邯郸 056038；2.河北省智慧水利重点实验室，河北 邯郸 056038）

1 引言

构建新型能源发展结构是缓解能源危机的重要途径。国家“十四五”规划和2035年远景目标纲要提出“推进能源革命，建设清洁低碳、安全高效的能源体系，大力提升风电、光伏发电规模”。因此，利用风能、太阳能、水能等可再生能源，探索风、光、水、储多能互补发展模式对当今社会的传统能源结构改革、国家能源安全具有重要意义。

我国是世界上水能资源最丰富的国家之一。最新水能资源普查结果显示，我国湖泊江河中水能理论蕴藏量、技术可开发量和经济可开发量分别达到6.94亿、5.42亿和4.02亿kW[1]，三者总量均为世界第一，为我国大力发展水电提供了先决条件。另外，由于光伏、风电受地理位置、季节等约束条件限制具有波动性、间歇性等缺点，单一光伏、风电或者风光互补系统在某一区域内难以保证足够的发电量，因此难以大规模普及。而水电较为灵活，将水电引入风光互补系统，形成“风、光、水、储”互补的新型能源利用模式[2]，充分发挥水电与蓄电池运行灵活、功率调节性佳的特点，既可弥补风光出力不足，又可平抑风光接入对电网稳定性的冲击[3]，因此建立风光水储多能互补系统对推动能源结构改革具有极大优势。

2 风光水储模型搭建

2.1 风电、光伏、水电、蓄电池特性

风力发电机在正常工作时由桨叶捕获风能，有效风能大小主要决定于风机特性即风能利用系数Cp

[4]，根据贝兹极限理论可知Cp＜0.593[5]，而经过计算机仿真得到的Cp为0.4～0.5。风能利用系数Cp与叶尖速比λ的关系曲线，如图1所示。

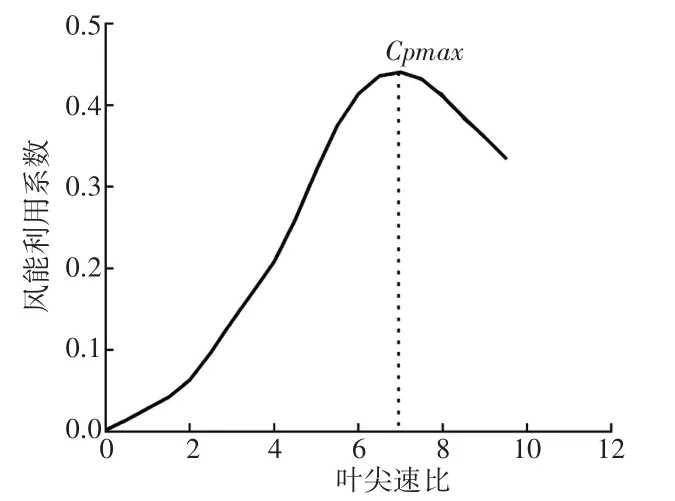
图1 风能利用系数Cp与叶尖速比λ关系曲线

光伏电池板是光伏发电的核心部件，在日常运行中受光照强度和环境温度影响较大[5]。本文对额定功率为450 W 的光伏电池板在不同环境条件下进行试验测试，光伏电池板工作特性曲线如图2所示，其中（a）和（b）分别为改变光照强度时光伏电池板的I-V、P-V工作特性曲线、（c）为改变环境温度时光伏电池板的P-V工作特性曲线。

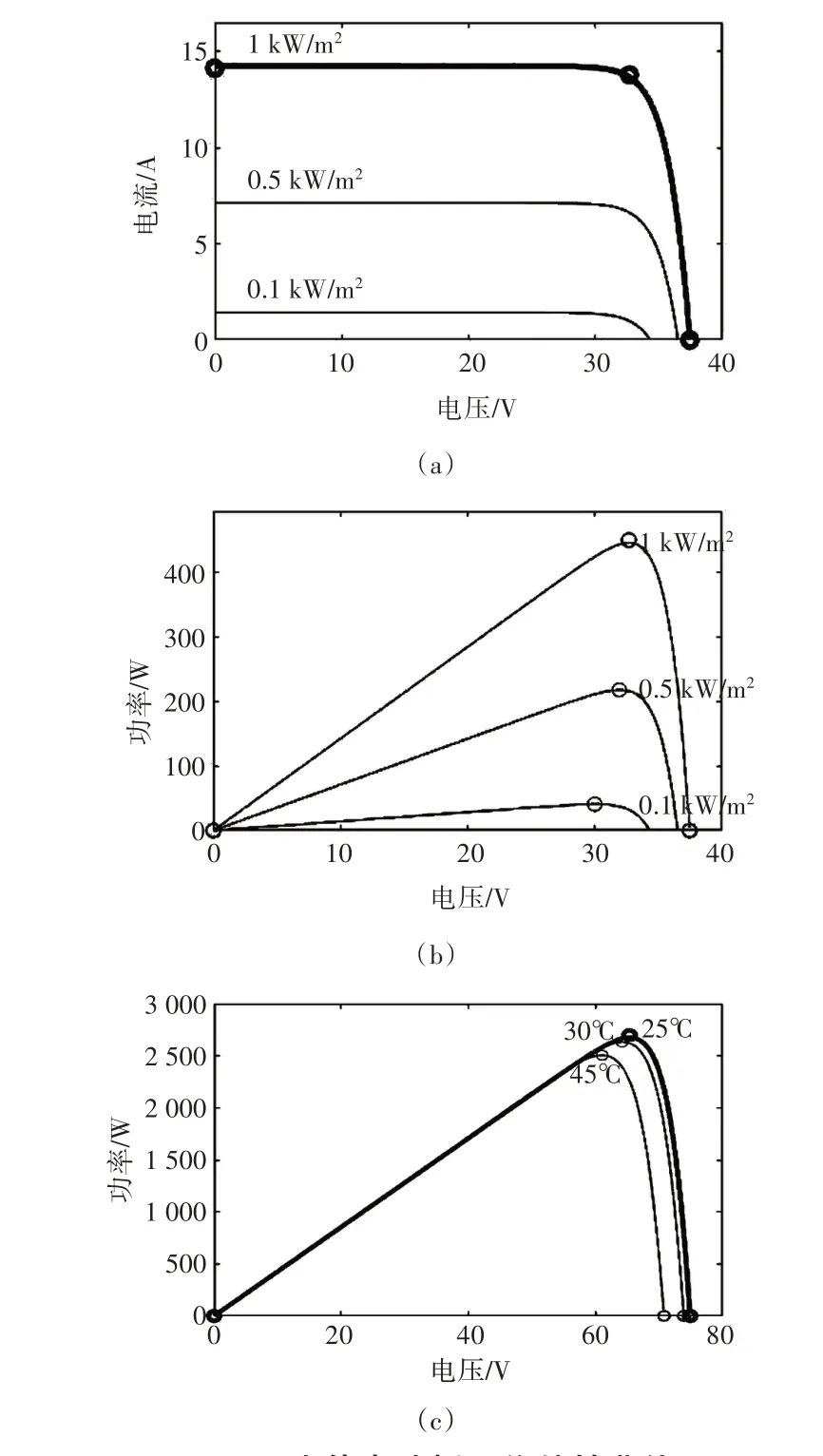
图2 光伏电池板工作特性曲线

水力发电机组具有开停机迅速、控制灵活的特点[6]，因而在多能互补系统中可以发挥调峰调频、平衡出力的作用。

蓄电池在风光水储多能互补系统中作为储能设备使用。当因天气因素使系统整体出力不足时可及时切换至蓄电池继续为负载供电[7]。由于风电、光伏多受制于地理环境因素影响，蓄电池的加入使得多能互补系统的运用更加灵活，即在蓄电池的调节下可以大大提高多能互补系统的适用性。

2.2 风光水储数学模型

2.2.1 水电数学模型

水轮机中最重要的两个参数是流量和力矩，流量代表设备的水力特性，力矩反映设备的机械特性[8]。根据水轮机的特性曲线可将力矩和流量转化为水轮机水头、转速以及导叶开度的相关函数表达式：

式中：Mt为力矩（N·m）；Q为流量（m3/s）；α为导叶开度（°）；H为水头（m）；n为转速（rpm）。

当水轮机各参数在较小幅度变动时，其传递函数为[9]：

式中：Mt（s）为经过拉氏变换后的力矩偏差相对值；Q（s）为经过拉氏变换后的流量偏差相对值；H（s）为经过拉氏变换后的水头偏差相对值；X（s）为经过拉氏变换后的转速偏差相对值；Y（s）为经过拉氏变换后的导叶开度偏差相对值；eh为水轮机力矩对水头的传函系数[10]，取1.5；ex为水轮机力矩对转速的传函系数，取-1；ey为水轮机力矩对开度的传函系数，取1；eqh为水轮机流量对水头的传函系数，取0.5；eqx为水轮机流量对转速的传函系数，取0；eqy为水轮机流量对开度的传函系数，取1。

在引水系统中，当水轮机转速发生变化时，调速器会对导叶进行相应的调整，因此会改变引水系统中流量与流速的大小。引水系统传递函数为：

式中：Gh（s）为经过拉氏变换后的引水系统传递函数；s为传递函数的频率响应；Tw为惯性时间常数[10]，取1.5。

调速器采用PID调速模型，其传递函数为[9]：

式中：G（s）为PID 模型传递函数；s为传递函数的频率响应；KP为比例系数，取0.2；KI为积分系数，取0.05；KD为微分增益系数，取0.05；Td为暂态反馈时间常数，取0.01。

2.2.2 光伏发电数学模型

对于常用光伏电池板，在光照强度S和温度Ta条件下，电池板两端产生电压为V时，其对应的电流计算公式如下：

式中：D为光伏板的修正系数；I为光伏板实际输出电流（A）；V为光伏板工作电压（V）；S为光照强度（W/m2）；Ta为环境温度（℃）；Tc为光伏板实际温度（℃）；DT为光伏板实际温度与标准温度的差值（℃）；DV为光伏电池板电动势与串联电阻电压差值（V）；DI为光伏板产生输出电压反作用于电池板的反向电流（A）；C1、C2为光伏板修正系数；tc为光伏板温度系数；Isc为标况光伏短路电流（A）；Voc为标况光伏开路电压（V）；Im为光伏电池最大功率时的电流（A）；Vm为光伏电池最大功率点处电压（V）；α为电流温度系数（A/℃）；β为电压温度修正系数（V/℃）；RS为光伏板串联电阻（Ω）；Sref为标况光照强度（W/m2），一般取定值1 kW/m2；Tref为标况温度（℃），取25℃。

2.2.3 风力发电数学模型

根据贝兹极限理论和伯努利方程以及连续性方程推导出风机输出数学模型为：

式中：Pm为风机输出功率（W）；ρ为空气密度（kg/m3），一般取1.225 kg/m3；λ为桨叶尖线速度与风速最佳比；ωr为风机转速（rpm）；π为圆周率；Cp为风能利用系数；ω为桨叶圆周线速度（m/s）；R为桨叶半径（m）；v为风速（m/s）；λi为叶尖速比系数；β为桨距角（°）；c1～c6为风机修正系数，由其特性决定，本文取值分别为0.5176，116，0.4，5，21，0.0068。

2.2.4 蓄电池数学模型

蓄电池数学模型为[7]：

式中：E为蓄电池组电动势（V）；E0为初始电动势（V）；K为极化电压常数；A为电压系数；B为容量系数；C为电池组初始容量（Ah）；Qn为电池组额定容量（Ah）；i(t)为充放电电流（A）；SOC为剩余荷电量（剩余电量比）；NES s为电池组件串联数。

为简化计算选用仿真工具箱内蓄电池组件按照DC-DC 升降压设计电路[11]，在仿真环境中搭建风光水储多能互补系统模型，其结构如图3所示。

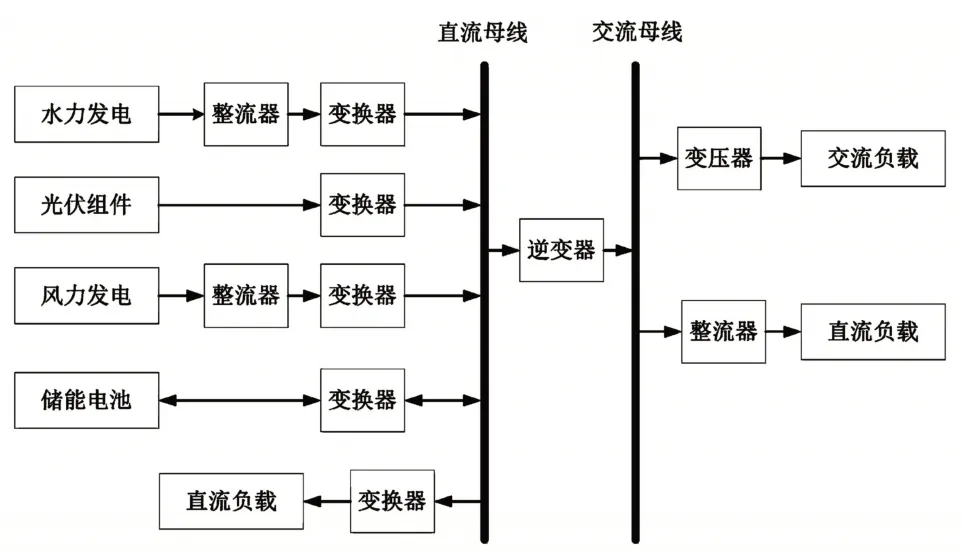
图3 风光水储多能互补系统结构示意

3 基于模糊逻辑控制的最大功率点追踪

本文采用模糊逻辑控制追踪最大功率点[12]。

3.1 模糊化计算

模糊逻辑控制方法需先将输入模糊化计算。设定模糊逻辑输入为误差E和误差变化量ΔE，当dP/dU=0 时，光伏和风电系统以最大功率运行。控制器对风光互补系统的输出电压和出力进行实时监控[13]。将此次采样数据设定为a，前次采样数据设定为a-1。本文使用双信号输入、单信号输出模糊控制规则设计控制法，即E（a）和ΔE（a）作为模糊控制器的输入量，占空比D的差值ΔD（a）为模糊控制输出量，公式为：

式中：E（a），E（a-1）为第a次，第a-1 次风电或光伏采集时的误差量（A）；P（a），P（a-1）为系统第a次，第a-1次采集时的风电或光伏输出功率（W）；U（a），U（a-1）为系统第a次，第a-1 次采集时风电或光伏的输出电压（V）；ΔE（a）为第a次，第a-1次风电或光伏采集时误差量的差值（A）；D（a），D（a-1）为第a次，第a-1 次采集时的占空比；ΔD（a）为第a次，第a-1次采集时占空比的差值。

当系统计算判定E（a）=0时，光伏电池和风力发电机的当前输出功率为最大功率，蓄电池不动作。

定义E、ΔE和ΔD皆为5个模糊子集，即：

E={NB,NS,ZO,PS,PB}，对应的论域为{-1,-0.5,0,0.5,1}；ΔE={NB,NS,ZO,PS,PB}，对应的论域为{-1,-0.5,0,0.5,1}；ΔD={NB,NS,ZO,PS,PB}，对应的论域为{0,0.2,0.4,0.6,0.8}。

定义中的NB,NS,ZO,PS,PB代表含义为负大，负小，零，正小，正大。隶属度函数采用高斯模糊三角形。

3.2 模糊控制规则

分析风、光P-D 特性曲线，当测得当前占空比D为正时，系统做出响应使输出功率增加，表明调整方向正确，保持当前调整方向；若系统做出响应使输出功率减少，则表明调整方向错误，系统将自动反向调整；当温度和日照强度发生变化致使风电和光伏的出力发生较大改变时，系统将迅速做出响应[13]。上述控制规则即输出变量ΔD与输入误差E和误差变化量ΔE的变化规则，目的是维持变量E为0。模糊控制规则，详见表1。

表1 模糊控制规则

3.3 反模糊处理

模糊控制输出是一个模糊集合，无法直接应用。需将输出模糊量进行反模糊化处理，得到清晰的控制量，直接控制被控对象。本模糊逻辑控制器输出结果已经过反模糊化计算处理，可直接输出结果。

4 仿真结果与分析

设定仿真步长最小为1 e-6 s，仿真时间为0.1 s，为了接近真实情况，进行3 次仿真计算。水轮发电机额定功率为1 kW，频率为50 Hz。风速条件设置为初始风速5 m/s，在0.1 s时间内分5步渐变至13 m/s达到额定风速。光伏条件设置3 种工况，工况1：20℃，800 W/m2；工况2：25℃，1000 W/m2；工况3：30℃，1200 W/m2。负载功率设定为3 kW。仿真模型参数设置如下：光伏电池板短路电流14.12 A，开路电压37.45 V，额定功率450 W。风机叶片半径1.3 m，额定风速13 m/s，额定功率500 W。蓄电池额定电压12 V，额定容量200 Ah。根据上述条件绘制风电、光伏、水电、蓄电池功率波形，如图4所示。

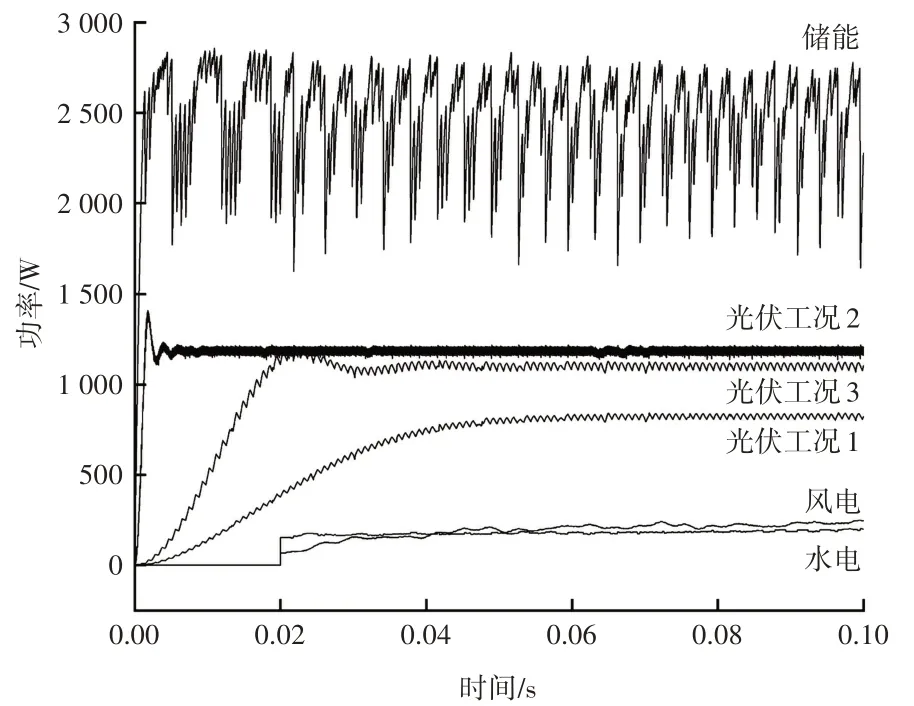
图4 风光水储功率波形

分析仿真模型输出波形可知：①由于优先消耗风光出力，水力发电在设定初始条件下随着仿真开始产生功率，与风光互补发电系统联合运行，在0.02 s 后达到相对稳定状态，此时水电提供相对稳定的0.2 kW功率。②光伏电池的3种工况模拟了1 d时间内光照强度和温度的近似变化，光伏模型在开始接收光照时直接产生功率，在较短时间内稳定在一定值，出力由开始的0.8 kW 上升至1.3 kW。③风电由于模糊逻辑控制作用稳定在0.25 kW。因仿真负载设定为3 kW，为使整体功率达到平衡，蓄电池处于放电状态，且会由于光伏出力的增大而相应减小，由1.75 kW 逐渐降至1.25 kW。风光水储整体出力与负载功率3 kW匹配，仿真结果符合实际情况。

5 结论

本文针对风力发电、光伏发电与水力发电的特性，建立风光水储多能互补系统，并利用MATLAB仿真构建了风光水储互补发电系统仿真模型。运用不断变化的PWM 信号控制开关管开断时间从而改变负载阻抗，实现光伏与风电的最大功率点追踪，从而优化风电、光伏、水电和蓄电池充放电控制模型，达到风光水储多能互补系统稳定输出效果。仿真模型设置3 种不同工况，结果与实际情况相匹配。试验表明，风光水储多能互补系统能够充分发挥风光水储的互补特性，为风光水储互补系统实际开发提供一定的参考依据。