基于博弈论-模糊综合评价法的长距离引水工程运行安全风险评价研究
2023-12-06李东可郭莹李小娟焦利民范天雨
李东可 郭莹 李小娟 焦利民,2 范天雨
(1.华北水利水电大学水利学院,河南 郑州 450045) (2.中国电建集团北京勘测设计研究院有限公司,北京 100024)
0 引言
长距离引水工程是解决水资源时空分布不均的有效途径,由于其工程规模大、地质条件、建筑物构成和运行环境复杂等特点,在运行过程中可能会出现多种风险事件,这些风险事件的发生会影响整个工程的运行安全,造成资源浪费和经济损失,严重的可能影响人民生命财产安全及社会安全稳定。因此,为了有效应对和管理风险事件,保证工程的安全持续运行,有必要对长距离引水工程运行安全风险进行综合评价研究。
引水工程是国民经济发展的主要基础设施,我国已经建成和正在建设的长距离引水工程的规模位居世界前列,众多学者对其运营的安全性问题展开了深入的研究。聂相田等[1]通过对长距离引水工程实际安全状况进行全面客观地评估,以及对影响其运行的安全风险因素进行全面地考虑,提出了一种评价集模型;杜霞等[2]对南水北调中线工程运行风险进行定性定量计算,在分析结果的基础上,提出了相关的控制措施,为其安全运行管理提供参考;李芬等[3]对冰害风险的空间分布进行研究,建立模糊评价模型,对冰害防治具有一定指导意义;王芳等[4]根据引调水工程中倒虹吸管身失稳险情的情况,建立一种以系统动力学为基础的风险分析反馈模型,为风险评估工作提供了一种新的方式。这些研究对长距离引水工程运行安全风险的认识和管控起到了重要的作用,但从系统整体出发对工程运行安全风险进行评价的研究较少。
综合评价是综合多个指标的信息对研究对象进行定量化的总体判断,目前已有的综合评价方法有粗糙集法、神经网络法和模糊综合评价法等。模糊综合评价法通过模糊数学的运算和可视化展示,可以使评价结果更加直观,方便评价者和决策者进行判断和决策。应用模糊数学方法建立数学模型的关键是建立符合实际的隶属函数。一般情况下,定性评价等级的隶属函数采用梯形分布、三角形分布或正态分布等[5-8]。正态分布函数能收集更多隶属度高的评价信息,屏蔽更多隶属度低的评价信息[8],评价结果较激进;三角形分布函数能收集更多隶属度低的评价信息,屏蔽更多隶属度高的评价信息,评价结果较保守,将两种评价结果加权平均,能够得出更为准确的评价结果。此外,指标权重是保证评价结果准确合理的关键,因此,需选择适当的方法来确定各指标的权重。将非结构性模糊赋权法和三角模糊数模糊赋权法两种方法相结合构成非结构三角模糊数赋权法,该方法的评价思路是从宏观到微观、先整体后局部,充分考虑到专家的悲观态度、中立态度和乐观态度[9];熵权法是一种通过对各个因素所能提供的信息进行全面分析,从而计算出一个综合性指标的数学方法,该方法的基本思想是通过对不同信息的差异来赋予权重[10];而基于博弈论的组合赋权法可以有效地克服主观赋权方法和客观赋权方法的缺陷,将两种方法相结合,达到了二者的平衡[11-12]。
因此,首先,运用非结构三角模糊数和熵权法分别计算指标主、客观权重;其次,利用博弈论求解各个风险指标的组合权重;最后,引入多交正态分布与三角形分布作为模糊评价等级的隶属函数分布,建立长距离引水工程运行安全风险评价模型。
1 长距离引水工程运行安全风险评价指标体系
在长距离引水工程运行过程中,突发事件诱因多且关系复杂,其性质、发展和演变过程、影响范围、影响程度和造成后果具有较大不确定性,受影响对象多,突发事件类别复杂,因此,建立科学有效的运行安全风险评价指标体系十分重要。经过收集资料、查阅相关文献分析,将可能出现的风险因素分为自然灾害风险、工程风险、社会安全风险、调度风险以及水质风险,并通过采用灰色关联度理论对风险因素进行指标优选,确定最终影响因素[13-14]。长距离引水工程运行安全风险评价指标体系见表1。

表1 长距离引水工程运行安全风险评价指标体系
2 基于博弈论的组合权重法
2.1 非结构三角模糊数确定主观权重
设D={D1,D2,D3,D4,D5}为专家集,Dk代表第k个专家;C={C1,C2,C3,C4,C5}为一级指标集,Cd代表第d个一级指标;Cd={Cd1,Cd2,Cd3,Cd4,Cd5}为一级指标Cd下的二级指标集,Cdi代表第i个二级指标,其中k=1,2,…,s;d=1,2,…,s;i=1,2,…,n。
(1)分层构建指标重要性排序。对一级指标Cb和Cd做重要性比较,用δbd表示其重要性程度。若Cb比Cd重要,则δbd=1,δdb=0;反之,则δbd=0,δdb=1;若两者同等重要,则δbd=δdb=0.5,δbb=δdd=0.5。构建指标值重要性排序矩阵公式如下
(1)
式中,b=1,2,…,m。
(2)构建三角模糊判断矩阵。根据式(1)求出的重要性排序,专家Dk给出各个指标三种态度的相对重要性判断矩阵,公式如下
(2)

(3)矩阵一致性检验。采用层次排序一致性检验方法。则期望值E(g)为
(3)
式中,0≤E(g)≤1,0≤λ≤1,λ的大小代表了专家的风险态度,通常取λ=0.5。根据式(2),求解出λ=0.5的期望矩阵
(4)
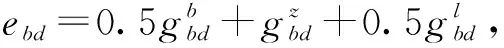
(5)
一致性比率为
(6)

(4)对k个专家评价信息进行加权平均,公式如下
(7)
(8)
(6)根据式(9)计算各指标的主观权重,得到
(9)
2.2 熵权法确定客观权重

(10)

(2)计算指标的差异系数hd。公式如下
hd=1-ed
(11)
(3)计算指标的熵权W″。公式如下
(12)
2.3 基于博弈论的组合权重计算
建立指标权重向量集βq={β1,β2,…,βP}(q=1,2,…,p),其中,p为求取权重方法的个数,本文p=2。设a={a1,a2}为线性组合系数。
(1)构造指标权重集。将两种权重向量在各个层次上进行线性组合,得到权重集
(13)
(2)求出最优权矢量。优化两个线性组合系数,获得最优矢量,建立目标函数
(14)
得到式(14)的一阶导数的最优条件
(15)
从而得到式(15)对应的线性方程组
(16)
根据式(16)求出(a1,a2)后,对其进行归一化,最后得出指标组合权重分别为
(17)
3 基于模糊理论的长距离引水工程运行安全风险评价模型
3.1 正态分布隶属函数
本文采用语言描述的定性评价等级,将长距离引水工程运行安全风险分为5级,即H={H1,H2,H3,H4,H5}={低风险,较低风险,中等风险,较高风险,高风险}。模糊评价等级集为H={Hy,y=1,2,…,Y},Hy为语言描述的定性评价等级。正态分布函数在μ±3σ范围中函数涵盖了99.73%的面积,因此常采用6σ作为函数的定义域。正态分布和三角形分布隶属函数比较如图1所示。
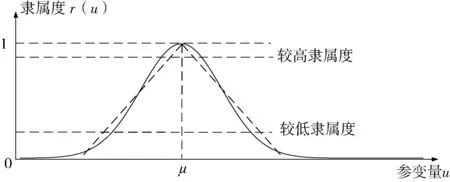
图1 模糊正态分布和三角形分布隶属函数比较
正态分布隶属函数的表达式为
(18)
(19)
(20)
(21)
(22)
上述公式中rH1(u)、rH2(u)、rH3(u)、rH4(u)、rH5(u)分别对应“低风险”“较低风险”“中等风险”“较高风险”“高风险”的正态隶属分布函数。根据以上分布函数确定正态分布隶属函数分布如图2所示。

图2 正态分布隶属函数
3.2 三角形分布隶属函数
根据正态分布隶属函数的参数及评价区间,得出三角形分布隶属函数的表达式为
(23)
(24)
(25)
(26)
(27)


图3 三角形分布隶属函数
3.3 模糊综合评价模型
专家将主观意识转移到对指标的评价中,根据自身经验对各个指标风险赋值,得到初始评价集合
Ud={ud1,ud2,…,udn}
(28)
根据待评价指标因素集和初始评价集合计算各个评价指标相对应的隶属度,对于每个单因素C单独作出评价,即为集合Cd到Ud的模糊映射f,f诱导出模糊关系Rf,Rf中的元素rnj即为隶属度。根据式(18)~式(27)得出各指标隶属风险等级的程度。即
f:Cd→Ud
(29)
式中,j为指标Cdn对评价等级j的隶属度,本文将风险等级分为5级,即j=5。
数据归一化处理
(30)
将评价指标因素的权重向量ω与归一化处理后的评价矩阵合成运算,得出每个一级指标评价等级隶属度
(31)
得出一级指标评价矩阵
(32)
进一步将一级指标权重向量ω与一级指标评价矩阵合成运算的出最终目标层评价等级隶属度
(33)
得出目标层风险等级评价结果见表2。

表2 目标层风险等级评价结果
将两种评价结果加权平均融合得到最终结果。
4 实例分析
4.1 工程概况
南水北调中线工程始于河南省淅川县的陶岔渠首枢纽,终于北京市,横穿长江、淮河、黄河和海河,总长度约为1432km。共有61个节制闸,95个分水口,1个泵站和众多类型建筑物,如倒虹吸,渡槽,无压涵洞等。南水北调中线工程的建设对解决北方地区的严重缺水问题、促进区域经济社会发展、提升人民生活水平等方面具有重要意义。本文以南水北调中线工程为例,进行安全风险因素评价。
4.2 确定指标权重
由5名相关领域的专家对各个指标进行打分,假设各层次的指标评分为100分,5名专家对该工程的一级指标打分表见表3。
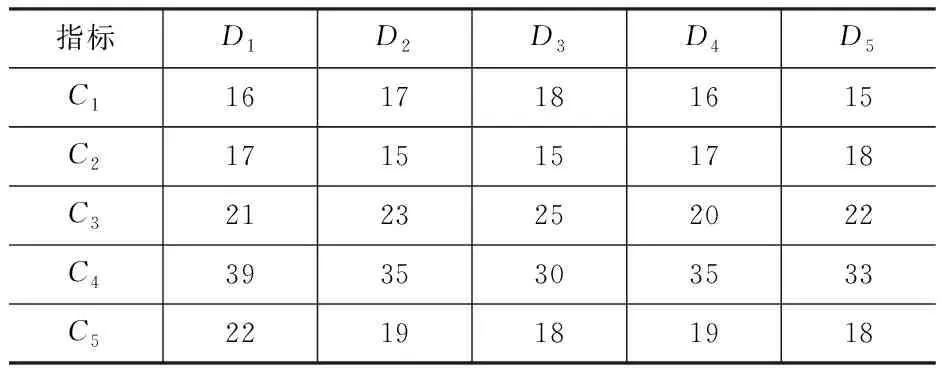
表3 专家对一级指标评分
根据2.1的内容对各指标权重进行分析。下面以一级评价指标为例进行计算分析。
专家Dk(k=1,2,3,4,5)各自对一级指标Cd(d=1,2,3,4,5)进行两两比较。根据式(1)和专家Dk的评分情况,构建指标重要性排序矩阵δ1,δ2,δ3,δ4,δ5,其中δ1指标重要性排序矩阵见表4。其他指标重要性排序矩阵同理可得。

表4 指标重要性排序矩阵
根据式(2)~式(6),对Gk进行一致性检验,均满足CR<0.1,通过一致性检验。
根据式(7)~式(9)求出一级指标的主观权重为W′=(0.160,0.121,0.240,0.280,0.199)。
结合表3专家对一级指标的评分情况,根据式(10)~式(12)求出一级指标的客观权重为W″=(0.131,0.175,0.202,0.299,0.193)。
根据式(13)~式(17)求出一级指标的组合权重为β*=(0.143,0.154,0.217,0.291,0.195)。
同理可求二级指标的权重。各指标权重见表5。

表5 各组合权重指标值
4.3 安全风险评价
4.3.1 正态分布隶属度计算
以一级指标自然灾害C1所包含的二级指标为例,说明隶属度的计算过程。根据式(18)~式(22),并结合图1,根据专家权重向量W=(0.2,0.25,0.15,0.3,0.1),五名专家对自然风险各指标的评价结果融合后见表6。
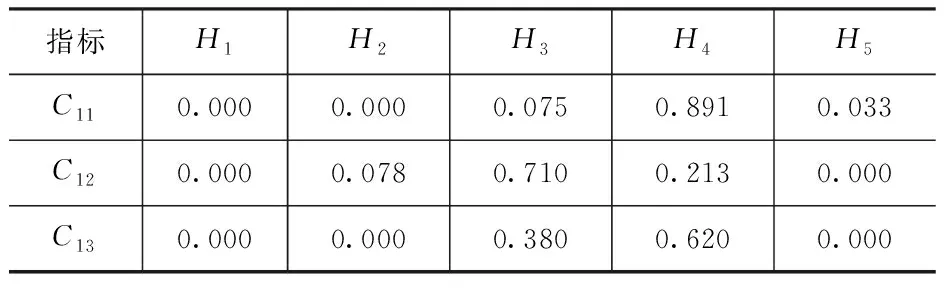
表6 融合后的自然灾害风险各等级隶属度
同理可得,五名专家对其余二级指标风险的评价结果。
根据式(33)求出五名专家对一级指标风险的评价结果融合见表7。
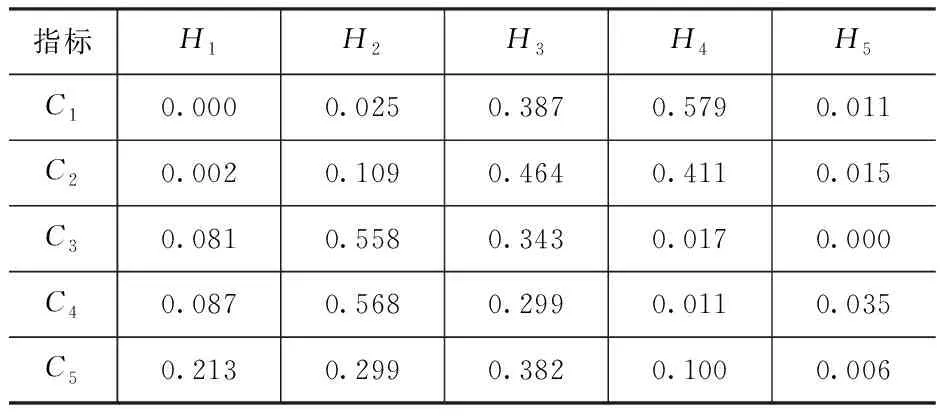
表7 融合后的一级指标各等级隶属度
根据式(35)求出长距离引水工程各等级隶属度分别为0.100,0.346,0.301,0.237,0.016。
4.3.2 三角形分布隶属度计算
同理,进行三角形分布隶属度计算。根据式(23)~式(35)求出长距离引水工程各等级隶属度分别为0.131,0.304,0.318,0.198,0.049。
将两种评价结果进行加权平均融合,求出一级指标评价结果见表8,南水北调中线工程运行安全风险评价结果见表9。

表8 一级指标评价结果

表9 南水北调中线工程运行安全风险评价结果
根据表9可知,工程运行安全风险模糊综合评价结果的隶属度为0.325,属于较低风险等级。根据表8可知,社会安全风险和调度风险模糊综合评价结果的隶属度为0.506和0.519,属于较低风险等级;工程风险和水质风险模糊综合评价结果的隶属度为0.425和0.318,属于为中等风险等级;自然灾害风险模糊综合评价结果的隶属度为0.520,属于为较高风险,应重点控制。
5 结语
运用灰色关联度法对风险因素进行指标优选,使评价更加全面、客观;运用非结构三角模糊数和熵权法并基于博弈思想确定综合权重,使指标权重更加合理;综合考虑多个因素和不确定因素,运用模糊理论,建立长距离引水工程运行安全风险评价模型,得出更为准确的评价结果;以南水北调中线工程为例进行评价分析,结果表明,工程风险总体处于较低风险,其中自然灾害风险处于较高风险等级,需要加强管控。
