斜拉桥初始检查及静载试验要点分析

陈继岳

（广东省交通运输建设工程质量检测中心 广州 510420）

0 引言

现今，无论是预应力钢筋混凝土、钢-混凝土组合、钢材料的斜拉桥，其跨径一般都大于150 m，属Ⅰ级养护检查的桥梁，初始检查非常重要，其检查结果是未来桥梁使用中各次检查的对比依据。本文依据《公路桥涵养护规范：JTG 5120—2021》［1］介绍斜拉桥初始检查及静载试验中的一些要点，并结合湛江某跨海大桥初始检查中静荷载试验的结构计算情况进行阐述。

1 工程概述

广东省湛江市某跨海大桥地处通明海域，连接东海岛和雷州市；大桥线路东起667 县道，上跨通明海域，西至黄雷东路；途经大桥线路为东海岛-雷州高速公路，项目于2021年12月建成通车。

该跨海大桥是桥跨布置为（146+338+146）m的双塔双索面半封闭钢箱组合梁斜拉桥，桥梁宽度38.5 m。主梁采用扁平流线形半封闭钢箱组合梁，所采用的组合梁主要轮廓尺寸为含风嘴全宽约38.5 m，不含风嘴顶板宽36 m，中心线处高度3.2 m（不含铺装），底板宽为（5.52+3.45+3.45+5.52）m。斜拉索采用1 770 MPa平行钢丝斜拉索，全桥共8×15=120 根斜拉索，最长约179 m，最大规格为PES7-313，单根最大重量约为126.6 t。主塔采用C50 混凝土，承台采用C40 混凝土，跨海大桥按车速100 km/h、双向6 车道高速公路标准设计，设计荷载等级为公路-Ⅰ级。

2 初始检查

单孔跨径大于150 m的斜拉桥属于Ⅰ级养护检查等级，初始检查前需收集好竣工资料、施工中的监理和监控资料。除了桥梁的总体尺寸、主要构件尺寸、截面尺寸、材料强度、外观质量等常规检查外，还需检查斜拉桥主梁和桥塔的控制截面内变形、桥面线形、全部拉索的拉力。这些检查数据是桥梁终身运营、养护维修最初始的依据。

2.1 变形观测点布置

对于一座新建的大桥，首先应在桥头两岸选择地基坚固，不易受到破坏和干扰的地方设置水准点或基准点，还应选取适当的备用点。可视新建大桥竣工时留下的这些点位，以方便今后观测桥梁变形为依据，确定是否需要移位和补充。其次是选择桥跨上的永久观测点，每孔不宜少于10 个点，沿行车道两边或靠缘石处布设，其中，桥的跨中、1/4 跨、桥墩支点等控制截面处必设。每个索塔不宜少于2个点，索塔顶面、塔梁交接处各1～2 点。最后绘制基准点、桥上永久观测点平面布置图，方便以后查找和利用。

2.2 桥面线形及成桥索力测量

这是测量新桥在成桥状态，无活载影响下，桥面上下游各永久观测点的高程、塔顶的初始水平位移，以及各拉索的拉力，这是将来判断桥面和塔顶是否变形、拉索的索力是否变化最原始的数据依据。

3 静荷载试验

通过中载（对称布载）和偏载加载对新建斜拉桥主梁、桥塔控制截面的内力和变形，以及典型拉索的拉力测量，计算各测点的校验系数，相对残余位移或应变、以及裂缝情况，判断桥梁的结构力学性能和工作状况是否满足设计要求。现行的斜拉桥主梁材料主要采用预应力钢筋混凝土、纯钢结构、钢梁-混凝土桥面板组合结构这3 种，近10 年来，后者应用越来越多，但《公路桥梁荷载试验规程：JTG/T J21-01—2015》［2］没有明确给出钢-混凝土组（混）合结构桥梁的校验系数常值范围，目前，暂按钢桥的校验系数常值范围取值，有待进一步积累资料来完善。静荷载试验涉及结构理论计算和现场加载试验测量，以下对理论计算分析和加载试验工况选择方面进行一些讨论。

3.1 结构理论计算

除了根据构件的受力性质，正确选择构件相应属性的单元，以及构件之间的约束和边界约束条件外，根据朱利明等人［3-4］的计算分析结果，根据现场实测数据对桥梁结构理论计算模型进行修正。

⑴考虑一半桥面铺装参与主梁受力，可使主梁应变和挠度校验系数分别提高4%和3%，对主梁和桥塔纵向位移影响较小。

⑵根据弹性模量实测值修正模型，可使主梁应变和挠度校验系数分别提高10%和9%，并减小了主梁和桥塔纵向位移。

⑶主梁有支座考虑支座摩阻对荷载试验计算值的影响很大。采用双折线模型考虑支座摩阻后，荷载试验应变和挠度校验系数分别提高了13%和21%，并修正了主梁梁端和桥塔塔顶纵向位移方向，使之与实桥实测一致。

3.2 计算参数及模型

采用空间有限元软件Midas/Civil 2020 建立湛江某跨海大桥的有限元空间模型，有限元建模时主要考虑结构的刚度、质量和边界条件，尽可能使有限元模型与实际桥梁结构接近。主塔、桥面板及主梁均采用梁单元，斜拉索采用只受拉桁架单元，模型共计离散760个单元和638个节点。

3.3 加载试验工况选择

加载位置取决于关注截面或控制截面的影响线范围，而关注截面或控制截面的位置取决于各包络图的最大值位置。对于斜拉桥来说，无论主跨、边跨（有辅助墩）和桥塔，先作出控制截面相应的弯矩包络图、塔顶水平位移和主梁竖向位移包络图，注意是活载的弯矩和位移包络图（现今很多试验报告未说清楚），其最大正弯矩和最大负弯矩处、最大位移处即为相应测点位置。一般对于大跨度斜拉桥来说，考虑加载试验工况时可关注以下问题［5-6］。

主梁弯矩包络图最大正弯矩位置与主梁挠度包络图最大挠度位置基本一致，相应影响线相近，两个测点的加载试验工况可以合并成一个加载工况。有些斜拉桥由于桥跨和拉索布置的情况不同，上述合并工况的试验加载位置会有一些出入，但考虑到桥梁运营中，达到设计极限状态的概率极小，对于新桥荷载效率系数取文献［2］的下限即可，这样可降低试验费用，节省试验时间，对桥梁结构也有好处。如该跨海大桥跨径布置为（146+338+146）m的双塔双索面半封闭钢箱组合梁斜拉桥，桥梁宽度38.5 m。有限元分析模型如图1 所示；汽车活载下主塔弯矩包络图如图2所示；汽车活载下主梁弯矩包络图如图3所示；汽车活载下结构最大变形图如图4所示。

图1 有限元分析模型Fig.1 Finite Element Analysis Model

图2 汽车活载下主塔弯矩包络图Fig.2 Bending Moment Envelope Diagram of Main Tower under Vehicle Live Load

图3 汽车活载下主梁弯矩包络图Fig.3 Bending Moment Envelope Diagram of Main Beam under Vehicle Live Load

图4 汽车活载下结构最大变形图Fig.4 Maximum Deformation of Structure under Live Load

由图2可知，在汽车活载作用下，桥塔的最大弯矩发生在桥塔根部，且两塔靠近岸边一侧的最大弯矩更大。从图3 的汽车活载下主梁弯矩包络图可以看出，中跨最大正弯矩位置与中点有些差异，这是由于桥塔和斜拉索的布置造成的。图5和图6分别给出了中跨主梁最大挠度：跨中挠度影响线和中跨主梁最大正弯矩：中跨弯矩影响线。

图5 中跨主梁最大挠度：跨中挠度影响线Fig.5 Maximum Deflection of Midspan Main Beam:Influence Line of Midspan Deflection

图6 中跨主梁最大正弯矩：中跨弯矩影响线Fig.6 Maximum Positive Bending Moment of Midspan Main Beam: Influence Line of Midspan Bending Moment

从图5 和图6 可看出，虽然中跨挠度和弯矩影响线的最大值位置有些错位，所以加载时可从跨中稍靠左边布载，对于新桥只要挠度和弯矩的荷载效率系数满足≥0.85 即可。图7 和图8 则分别给出了左边跨主梁最大挠度：边跨挠度影响线和左边跨主梁最大正弯矩：边跨弯矩影响线。

图7 左边跨主梁最大挠度：边跨挠度影响线Fig.7 Maximum Deflection of Left Span Main Beam:Influence Line of Side Span Deflection

图8 左边跨主梁最大正弯矩：边跨弯矩影响线Fig.8 Maximum Positive Bending Moment of left Span Main Beam: Influence Line of Side Span Bending Moment

从图7 和图8 可看出，边跨的挠度影响线和弯矩影响线的最大值位置基本一致，同一载位加载时，左边跨主梁挠度和弯矩的荷载效率系数都不低。

桥塔弯矩包络图最大弯矩位置与塔顶位移包络图最大水平位移位置基本一致，即相应影响线相近，两个测点的加载试验工况也可以合并成一个加载工况。该座斜拉桥其桥塔最大弯矩和塔顶最大水平位移位置处的影响线如图9和图10。

图9 左塔梁结合处桥塔的弯矩影响线Fig.9 Bending Moment Influence Line of Bridge Tower at the Junction of Left Tower and Beam

图10 左桥塔顶部的水平位移影响线Fig.10 Horizontal Displacement Influence Line at the Top of Left Bridge Tower

从图9 和图10 可看出，塔梁结合处桥塔弯矩影响线和塔顶水平位移影响线的最大值位置基本一致，图形也相近，同一载位加载时，左桥塔弯矩和位移的荷载效率系数也都不低。

典型拉索的索力测量，所谓典型拉索应该理解为：当拉索的钢丝截面积相同时，就是拉力包络图中拉力最大的那根（对）索；当拉索的钢丝截面积不相同时，就是拉应力包络图中拉应力最大的那根（对）索。计算出该索的影响线后即可按最不利布载，算出该索的最大拉力。该桥试算出靠左塔顶的中跨拉索拉应力最大，其索力影响线如图11所示。

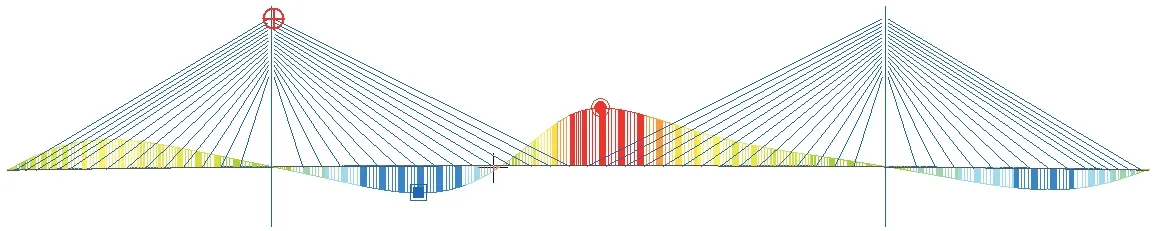
图11 塔顶的中跨拉索的索力影响线Fig.11 Cable Force Influence Line of Mid-span Cable on the Left Tower Top

从图11可看出，该索的索力测量如果中跨布载计算的荷载效率系数不足的话，还需左边跨加载。

3.4 加载试验工况分析［7］

经对比分析各控制截面影响线，可将该跨海大桥荷载试验方案进行优化：边跨主梁最大正弯矩及挠度合并为工况1，而主塔弯矩、主塔偏位、主梁最大正弯矩及挠度合并为工况2，各工况设置控制项目及荷载试验效率如表1所示，各工况的加载效率符合文献［2］相关规定，据此可以认为静载试验结果准确合理，各工况试验评价指标计算如表2所示。

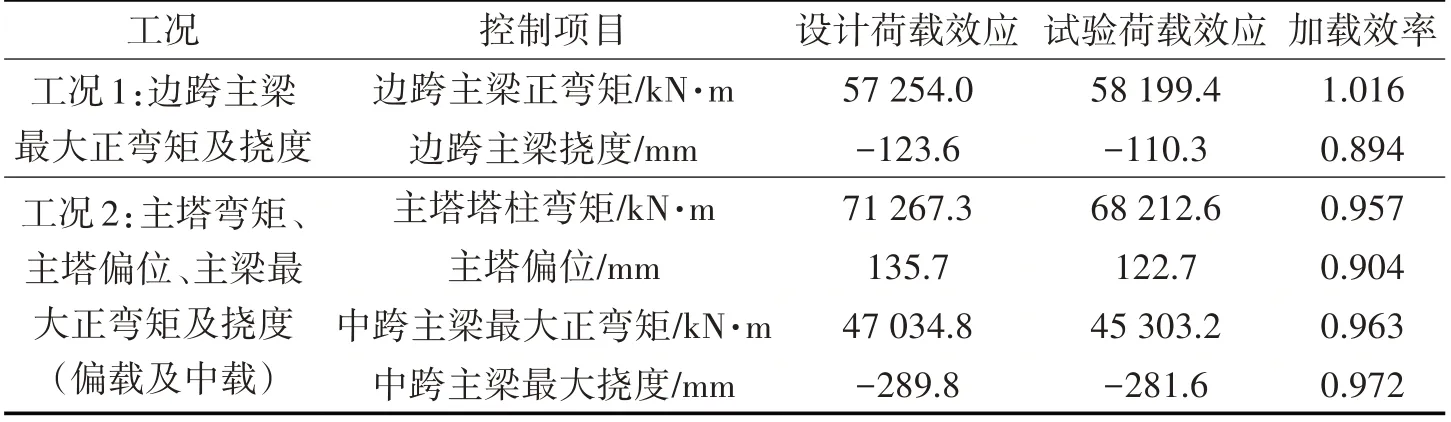
表1 各工况试验荷载效率Tab.1 Test Load Efficiency under Various Working Conditions

表2 指标计算综合表Tab.2 Comprehensive Table of Index Calculation

由表2可得［8］，各工况试验荷载作用下，所有工况评价指标的校验系数均小于1，均在文献［2］要求的常值范围内，主塔各控制指标的校验系数均位于文献［2］第5.7.8 条关于预应力混凝土要求的常值范围，结构性能满足设计要求。同时，主梁除边跨最大正弯矩截面挠度略低于文献［2］第5.7.8条关于钢桥校验系数的常值范围内，进一步表明该桥的承载能力和安全储备足够高。另外，还可以看出边跨主梁的最大正弯矩截面应变和最大竖向位移的校验系数均小于中跨的结果，这主要是和跨径布置和受力模式有关。总之，该桥的强度和刚度均满足文献［2］要求，且具有足够的储备。

另外，各试验工况控制截面的相对残余变形（或应变）介于-4.7%～12.0%之间，均满足文献［2］第5.7.8条关于主要控制测点的相对残余变形（或应变）不宜大于20%的要求。众所周知［9-10］，残余变形是衡量桥梁结构弹性恢复力的一个重要指标，当前各工况控制截面的相对残余变形远小于20%，足可表明桥梁结构具有较好的弹性工作状态，变形储备较多，抵抗外荷载作用的能力较强。

同时，在静载试验过程中，未发现明显新增裂缝。这说明在试验荷载作用下，桥梁结构的裂缝处于稳定状态，没有进一步发展的趋势，结构的刚度较好，安全性得到足够保障。

需要说明的是，文献［2］没有明确给出钢-混凝土组（混）合结构桥梁的校验系数常值范围，目前，暂按钢桥的校验系数常值范围取值，有待进一步积累资料来完善。

本文通过湛江某跨海大桥的成桥静载试验为工程背景，运用内力控制截面的概念对原荷载试验工况进行了优化。对工况优化过程中存在一些难以确定的因素和相关假设，但通过细化计算和比对计算，提出更优的静载布载方案，并大大提高了桥梁静载试验结果的准确性。［11］采用文章中的优化合并方法很好地完成了湛江某跨海大桥的静荷载试验，荷载试验表明：该跨海大桥在试验荷载作用下，结构实际受力状态与理论计算模式下的受力状态基本吻合，结构具有足够强度储备，材料处于弹性受力状态。

4 结语

对于斜拉桥的初始检查应特别注意基准点、桥上永久观测点的长期设置，并绘制平面布置图保存，方便后人查找和利用；静荷载试验的结构理论计算时，可以考虑实桥的弹性模量、支座摩阻及铺装层对计算结果的影响；确定试验加载位置时尽可能将斜拉桥的主梁最大正弯矩和最大挠度测试合成一个加载工况，工况优化合并后，各控制断面的加载效率均满足文献［2］要求，在保证了荷载试验有效的情况下，以便减少现场荷载试验时间及成本。