基于均布荷载面变化率的桥梁损伤识别

朱秀清，曹绍林，2，唐伟军，2

（1、广州市盛通建设工程质量检测有限公司 广州 510075；2、暨南大学信息技术研究所 广州 510075）

0 引言

桥梁承担景观效果及交通节点的重要功能［1］，而随着桥梁服役时间的增长、气候和环境等自然因素的长期作用以及交通量和重车数量的不断增加，桥梁结构的安全性、适用性和耐久性也必然发生退化，极端情况下将引发灾难性的突发事故［2］。因此对桥梁结构进行健康监测，及早发现桥梁损伤，选择合适的桥梁修补方案对延长桥梁使用寿命，对保护人民生命财产安全有重大意义［3］。

桥梁结构发生损伤时会导致结构的动力参数发生变化，因此可以通过结构的模态分析得到动力参数进行损伤识别，其中以模态振型［4］、固有频率［5］等动力参数的方法为例，由于其相较于挠度［6］、应变［7］等静力参数包含了更多损伤信息，所以基于模态振型与固有频率的损伤识别方法引起了国内外学者的广泛关注。KO 等人［8］提出了基于模态数据的柔度变化率损伤指标，为香港汲水门斜拉桥进行多阶段损伤检测，结果表明基于模态数据的柔度变化率能够检测到损伤位置；郭金泉等人［9］通过对模态振型进行平稳小波变换处理来检测悬臂梁的微小缺陷，研究了不同损伤程度、不同损伤位置对悬臂梁损伤识别的影响，结果表明该方法可以对损伤进行精确定位，而且随着损伤程度的增大，损伤指标值也在增大，可以定性比较损伤程度的大小；吴桐等人［10］通过公式推导得到损伤前后的曲率模态曲线所围成的面积变化作为损伤定位参数来进行损伤位置的识别，结果表明该方法在多种损伤工况中都能有良好的效果；周奎等人［11］提出基于柔度曲率矩阵的损伤指标对一人行天桥进行结构分析，结果表明该方法对于人行天桥具有良好的损伤识别性能，并且具有一定抗噪性和识别微小损伤的能力；YOON 等人［12］通过曲率模态数据与平滑数据的绝对差值来定义损伤指标，再使用不等式异常值检测方法对损伤指标进行统计处理，以建立检测损伤的置信水平来识别损伤，结果显示该方法具有良好的损伤识别效果。尽管国内外学者提出了大量损伤指标，但是每个指标都有自己的局限性，有的指标只能进行损伤位置的识别，不能定性比较损伤程度大小；有的指标抗噪声能力差，容易受环境影响；有的指标灵敏度低，只能识别较大程度的损伤。

本文提出一种均布荷载面变化率的损伤新指标，通过与曲率模态差与振型差两个传统指标对比，对简支梁模型进行多种损伤工况的识别分析，验证该损伤指标的有效性。

1 理论基础

1.1 振型差

将损伤前后的模态振型值作差，即可得到模态振型差损伤指标计算公式

1.2 曲率模态差

Pandey 和Biswas［13］提出通过中心差分法近似计算结构振型的模态曲率：

式中：φij为第i阶第j个测点的模态振型值；为损伤前第i阶第j个测点的曲率模态值；为损伤后第i阶第j个测点的曲率模态值。

1.3 均布荷载面变化率

PANDEY 等人［14］提出结构的柔度矩阵F可近似表示为：

式中：ωi为第i阶固有频率；φi为第i阶振型。

ZHANG 等人［15］基于柔度矩阵提出了均布荷载面的定义，其变形等效于各个节点施加单位载荷，均布荷载面公式表示为：

式中：m为模态阶数；φik为第k阶第i个测点的模态振型值。

为了实现对结构损伤位置更好的定位，提出均布荷载面变化率的定义，公式表示如下：

2 数值模拟

2.1 材料参数、几何参数及损伤工况

利用商业有限元软件ANSYS建立一简支梁模型。简支梁模型材料设置为钢材，材料参数：密度为7 850 kg/m3，弹性模量为210 GPa，泊松比为0.3；几何参数：简支梁截面形状为矩形，简支梁全长L=20 m。将简支梁模型沿长度方向划分为200个单元。将一质量块作为激励源，质量块移动速度为1 m/s。采样频率设置为200 Hz。简支梁模型简化图如图1所示。

图1 简支梁模型Fig.1 Simple Bridge Model

损伤位置设置在梁的0.4l和0.7l位置处，通过删除模型的单元来设置不同程度的损伤，分别为10%，20%，30%的损伤程度，工况如表1所示。其中相对位置为无量纲单位。

表1 工况设置Tab.1 Scenarios Setting

简支梁模型前2 阶固有频率分别为1.14 Hz 和4.56 Hz。

2.2 数值模拟结果

提取简支梁模态振型，计算工况2 和工况3 的一阶振型差，红色标记点表示损伤位置，损伤识别结果如图2⒜和图2⒝所示。可以看到，当发生单一损伤的时候，在梁的0.4l或0.7l位置处，振型差损伤指标存在突起，成功识别到损伤位置。

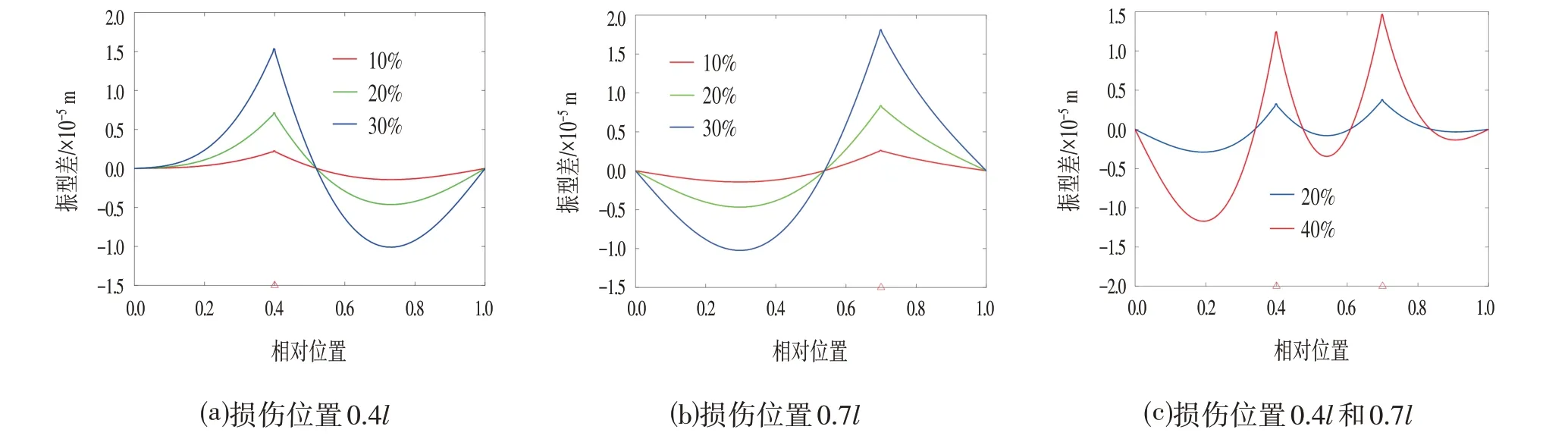
图2 计算工况的一阶振型差的损伤识别结果Fig.2 Damage Identification Results of First-order Pattern Difference in Calculation Conditions

计算工况4的一阶振型差，损伤识别结果如图2⒞所示。可以看到，当发生两处损伤时候，在梁的0.4l和0.7l位置处，振型差损伤指标存在突起，成功识别到损伤位置。

如图2所示，虽然损伤指标一阶振型差无论在单损还是双损的工况下都能精确地识别出损伤位置，但是损伤指标值的量级过小，在实际情况中损伤信息容易被其它因素掩盖，造成损伤识别结果的误判或者漏判。

通过结构的模态分析，提取简支梁的模态振型，分别计算工况2 和工况3 的一阶曲率模态差，损伤识别结果如图3⒜和图3⒝所示。可以看到，当发生单一损伤的时候，在梁的0.4l或0.7l位置处，一阶曲率模态差损伤指标存在突起，成功识别到损伤位置。

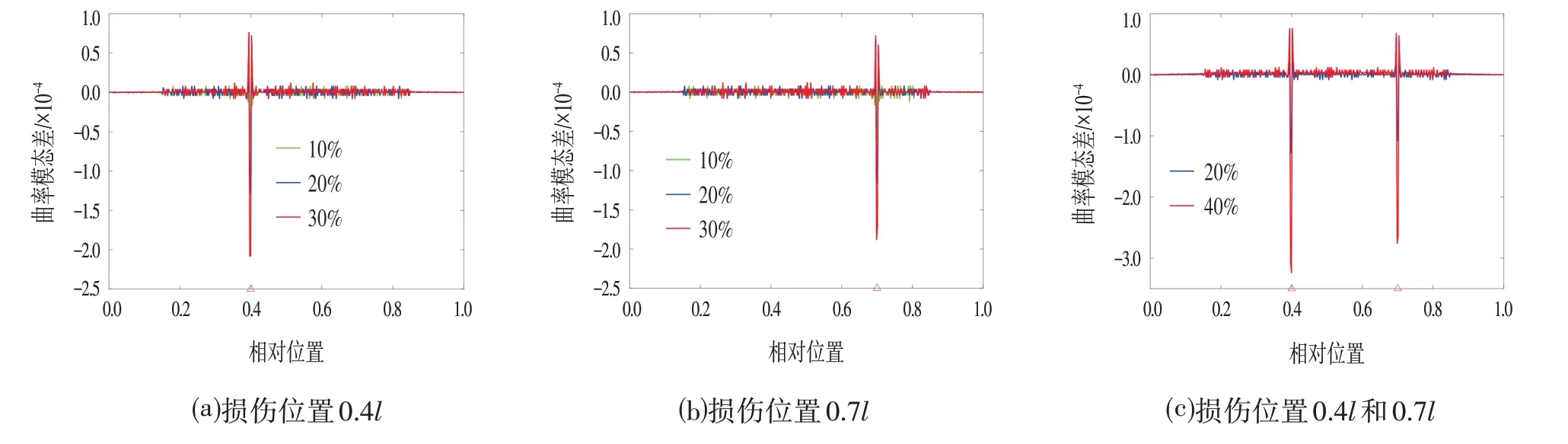
图3 计算工况的一阶曲率模态差的识别结果Fig.3 Damage Identification Results of the First-order Curvature Mode Difference in the Calculation Condition

计算工况4 的一阶曲率模态差，损伤识别结果如图3⒞所示。可以看到，当发生两处损伤时候，在梁的0.4l和0.7l位置处，振型差损伤指标存在突起，成功识别到损伤位置。

如图3所示，虽然损伤指标一阶曲率模态差无论在单损还是双损的工况下都能精确地识别出损伤位置，但是损伤指标值的量级过小，在实际情况中损伤信息容易被其它因素掩盖，造成损伤识别结果的误判或者漏判，而且用二阶中心差分求曲率的方法会放大振型中原有噪声，这也会造成损伤识别结果的误判或者漏判。

为了克服以上缺点，提出均布荷载面变化率新损伤指标来识别损伤位置。提取前2 阶模态参数，计算工况2 和工况3 的均布荷载面变化率，损伤识别结果如图4⒜和图4⒝所示。可以看到，当发生单一损伤时候，在梁的0.4l或0.7l位置处，均布荷载面变化率损伤指标存在突起，成功识别到损伤位置。

图4 均布荷载面变化率损伤识别结果Fig.4 Damage Identification Results of Uniform Load Surface Change Rate

计算工况4 的均布荷载面变化率，损伤识别结果如图4⒞所示。可以看到，当发生两处损伤时候，在梁的0.4l和0.7l位置处，均布荷载面变化率损伤指标存在突起，成功识别到损伤位置。而且随着损伤程度增大，损伤指标值也在增大，可以以此判断桥梁损伤的严重程度。损伤指标值量级相较于两个传统指标较大，不易受环境因素影响，更加适用于实际工程。

2.3 噪声鲁棒性

由于在实际情况中会有各种噪声的影响，而数值模拟是在完全理想化的情况下进行的，所以为了进一步验证该损伤指标的噪声鲁棒性，将模态分析中的模态振型值添加70 dB的高斯白噪声。信噪比可以衡量噪声大小水平，信噪比公式表示为：

式中：m(n)为原始信号；d(n)为噪声信号；Am为信号m(n)的均方根；Ad为信号d( )n 的均方根，信噪比的单位为分贝（dB）。

添加70 dB的噪声后均布荷载面变化率损伤识别结果如图5 所示。可以看到，无论是单损还是双损的工况，均布荷载面变化率均能在损伤位置存在突起，可以对损伤进行精确定位，表明该指标具有一定的抗噪性，符合实际工程的应用。

图5 添加噪声后均布荷载面变化率损伤识别结果Fig.5 Damage Identification Results of Uniform Load Surface Change Rate after Adding Noise

3 结论

本文利用模态分析得到简支梁模态振型，基于模态振型计算均布荷载面变化率，将其作为损伤指标进行损伤定位。本文主要结论如下：

⑴本方法利用均布荷载面变化率新损伤指标，能够精准识别损伤位置。

⑵均布荷载面变化率具有一定的抗噪能力，可以应用到实际工程中。