锚桩法静载试验群桩相互作用解析分析

魏仕锋，吕 军，石汉生

（广东省建筑设计研究院有限公司 广州 510010）

0 引言

桩基静载试验是检验单桩承载力最直接可靠的试验方法，按照反力系统不同可分为堆载试验法和锚桩试验法。堆载试验法需运送大量配重块，吊装运输成本高，开展大吨位试验存在较大的安全风险。相比前者，锚桩试验法无需吊运试块，也不用对场地地基进行加固处理，其安全性显著提高。锚桩试验装置平面布置示意图如图1 所示。试桩和锚桩通过主梁、副梁组成完整的加载体系，通过千斤顶对试桩施加垂直向下的竖向荷载，其上拔反力荷载则通过主梁和副梁传递至各锚桩，试桩承受的竖向荷载等于各锚桩所受垂直向上荷载之和。锚桩法试验过程中，试桩和锚桩桩周土体变形相互叠加。如图2 所示，随着荷载不断增大，试桩和锚桩的相互作用越来越明显，锚桩周边土体向上位移场将影响试桩竖向刚度和变形，同时试桩周边土体向下位移也会影响锚桩位移，现场记录的试桩沉降和锚桩上拔位移就是二者相互作用的结果。

图1 锚桩法试验装置平面示意图Fig.1 Diagram of Anchor Pile Method Test Device

图2 试桩和锚桩相互作用示意图Fig.2 Diagram of Interaction between Test Pile and Anchor Pile

目前，已有不少学者围绕锚桩静载试验开展研究。曹文昭等人［1］采用数值分析和现场试验分析锚桩-堆载联合法中支墩和锚桩承、卸荷过程对试桩的影响；卢铖昀［2］基于某铁路项目桥梁桩基锚桩静载试验，对比分析中国与欧洲标准中锚桩法静载试验的差异；李浩年等人［3］利用H 型钢桩作为锚桩进行单桩抗压静载试验，解决了受场地条件限制的难题；张铁柱等人［4］运用有限元软件分析锚桩不同布置方式和设计形式下试桩的受力情况；周洪波等人［5］介绍一种采用新型快捷连接装置的锚桩横梁反力装置及其在管桩抗压静载试验中的实施方法；李超华［6］运用有限元法分析不同锚桩方案对试验结果的影响，认为锚桩与承压桩距离足够大时锚桩对结果的影响可忽略。

现有研究主要采用数值建模和现场试验进行锚桩和试桩相互作用分析，适用于锚桩法静载试验的解析计算模型尚未建立。本文提出基于弹性理论法的抗拔单桩解析计算模型及考虑试桩-锚桩相互作用的群桩计算模型，讨论不同地层中抗拔桩桩身变形和内力分布规律，以及地层条件、桩间距等对试桩竖向抗压刚度和变形的影响，以期为锚桩静载试验方法的实际应用提供理论指导。

1 本文计算方法

本文基于弹性半无限空间Mindlin 位移解答，引入土体分层和非线性特性，建立考虑土体弹塑性变形的抗拔单桩理论计算模型，分析抗拔锚桩的桩土界面应力与位移分布特性。抗拔单桩主要计算步骤如下：

⑴假定桩侧和桩端扩底单元界面的剪应力和压应力为均匀分布，通过对桩侧和桩端扩径面积进行数值积分，求得各单元土体位移与应力的关系，进而得到桩周土反力与土体位移的关系式，即：

式中：{s1} 为土体位移列向量；{Rs} 为桩周土反力（包括桩侧和桩端阻力）列向量；[Gs]为土体柔度矩阵。

⑵根据杆系有限元理论，将桩简化为采用结点连接的杆单元，通过联立各单元刚度矩阵得到桩身整体刚度矩阵[]Kp，以及桩身位移与荷载的关系式：

式中：{s2} 为桩身结点位移列向量；{Q} 为桩顶上拔荷载列向量。

⑶将式⑴对[]Gs求逆后代入式⑵，假定桩-土界面无相对位移产生，即{s1} ={s2} ，得到桩-土体系的总体控制方程：

求解式⑶得到桩身各计算结点的上拔位移量，进而求得桩周土反力和桩身向上轴力。

⑷对于由受压试桩和n根抗拔锚桩构成的锚桩静载试验系统，将上述单桩模型与位移叠加原理结合，建立如下抗拔锚桩-受压桩耦合分析的位移方程：

式中：[Kpg]为由试桩竖向刚度矩阵[Ks]和锚桩竖向刚度矩阵[Kmi]组成的群桩体系总体刚度矩阵，其展开式为：

式中：{wp} 、{Qp} 和{Rs} 分别为各桩桩身结点位移列向量、外荷载列向量和土反力列向量，其展开式为：

式中：Qmi为静载试验第i根锚桩受到的上拔荷载，假定各锚桩承受完全相同的荷载，则有Qmi=Q1/m（i=1，2，…，i，…，n）。

⑸抗拔锚桩和试桩周边土体位移方程表示为：

式中：{ws} 和{Rs} 分别为与试桩和锚桩桩身结点对应的土体结点位移列向量和反力列向量；[Gss]为所有桩周土结点组成的土体柔度矩阵，即：

式中：[Gmi,mj]为锚桩mj各桩-土结点相互作用力引起的相邻锚桩mi的桩身变形；[G1,mj]为锚桩mj各桩-土结点相互作用力引起的试桩桩身变形；[Gmi,1]为试桩各桩-土结点相互作用力引起的锚桩mj的桩身变形，可根据单位荷载作用点与被影响点的位置按Mindlin位移解公式计算。

⑹根据桩土界面位移协调条件，建立试桩-锚桩-土体整体控制方程，即：

通过给定试桩和锚桩顶部荷载可直接求解式⑼，得到各桩土结点的位移和反力。当给定锚桩、试桩桩土界面应力极限值后，按荷载增量法进行求解。通过上述步骤，得到抗拔单桩非线性荷载-沉降关系及各级荷载下桩-土相互作用力。

2 参数分析工况

为评价场地条件对抗拔锚桩承载性能的影响，首先建立不同地层条件下抗拔单桩计算模型，然后建立静载试验抗拔锚桩-试桩相互作用计算模型，分析静载试验过程中锚桩上拔对试验桩承载性能的影响规律。分析工况如下：

⑴工况A：均质地基。假定桩基和土体模型均为线弹性，桩径D=1 m，Ep=30 GPa，长径比lp/D=25，桩土模量比Ep/Es分别取100、500、1 000、5 000。土体泊松比ns取0.3。

⑵工况B：分层地基。如图3 所示，桩径D=1 m，Ep=30 GPa，长径比lp/D=25。地基土共3层，土体泊松比ns取0.3，深度h以下为基岩。桩土模量比Ep/Es为1 000。

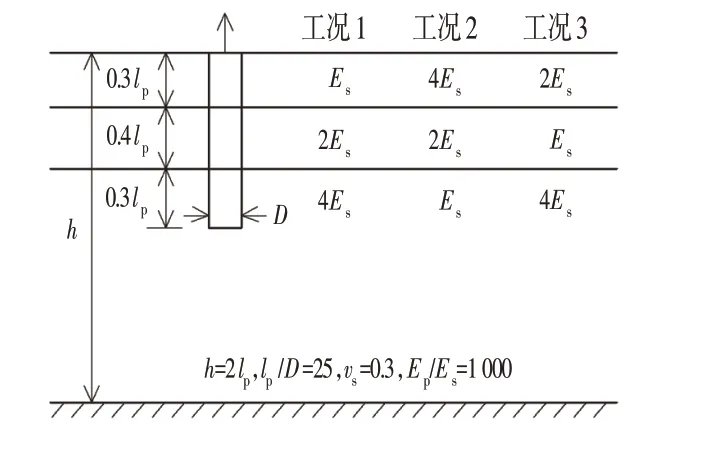
图3 单桩分层地基计算工况示意图Fig.3 Diagram of Calculation Conditions for Single Pile Layered Foundation

⑶工况C：场地类型包括半无限地基、有限深度地基和分层地基，如图4所示。桩间距比s/D为2～10，长径比lp/D=5～50，桩土刚度比Ep/Es=100～10 000。对于有限深度土层中的桩基础，土层深度比h/L为1～5，其中Ep为桩弹性模量，s为桩间距。土体泊松比为0.3。

图4 计算工况示意图Fig.4 Diagram of Calculation Conditions

3 计算结果分析

3.1 工况A结果

长径比lp/D=25 时均质土层中抗拔单桩的内力和变形与深度的关系曲线如图5 所示。图5 中纵坐标深度（z/lp），横坐标桩侧阻力（fs·π Dlp/Qtop）、桩身轴力（N/Qtop）和上拔位移（w/D）均采用无量纲方法处理。可以看出，在桩身弹性模量给定的前提下，桩土刚度比Ep/Es越大（土体弹性模量越小），桩-土界面摩阻力和桩身轴力曲线沿深度变化幅度越小，相应桩身上拔位移量越大。当位于软弱土层中时，桩基的竖向抗拔能力最低。

图5 均质地基计算结果Fig.5 Calculation Results of Homogeneous Foundation

3.2 工况B结果

分层地基中抗拔单桩的内力和变形与深度的关系曲线如图6所示。当桩段位于土体模量大的地层中时，其桩侧抗拔单位摩阻力发挥水平最大，桩身轴力衰减最快。在不考虑土体极限承载力前提下，得到的桩侧阻力和桩身轴力曲线在任意大小上拔力作用下均满足该规律。相同上拔荷载作用下工况2的桩顶上拔位移量最小，工况3次之，工况1最大。但是，工况2桩身下部位移大于其他两种工况，这主要与下层土竖向刚度较上层土偏低有关。当桩基用于承担上拔荷载时，浅部土层性质对承载力发挥起到重要作用。

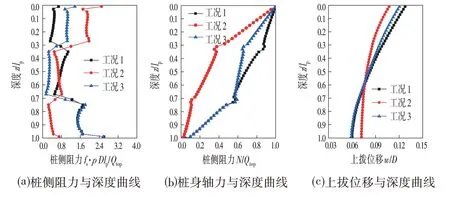
图6 分层地基计算结果Fig.6 Calculation Results of Layered Foundation

3.3 工况C结果

将考虑锚桩影响和不考虑锚桩影响的试桩竖向抗压刚度比值定义为Fc。由图7可以看出，即便按《建筑基桩检测技术规范：JGJ 106—2014》［7］要求的桩间距比取4 进行锚桩法静载试验，Fc值也可能超过2，即实测试桩沉降量不足真实沉降量的一半，试验结果可能高估试桩的初始抗压刚度。随着桩间距比增加或桩土刚度比降低，Fc计算值减小，并且数值分布区间变窄。对于较小的桩土刚度比，Fc值随桩长径比降低而增加。对于较大的桩土刚度比，Fc值随桩长径比增加而增大。

图7 半无限均质地基摩擦桩竖向抗压刚度比FcFig.7 Vertical Compressive Stiffness Ratio Fc of Friction Piles on Semi Infinite Homogeneous Foundation

对有限深度均质地基中的摩擦桩和端承桩竖向刚度比Fc进行计算。如图8 所示，当桩长径比设置为25时，位于半无限土体中摩擦桩的Fc值都大于有限均质土层中的Fc计算值。两类地层中Fc值的发展趋势基本一致。随着桩间距比增大或桩土刚度比减小，Fc的计算值减小并且该值的分布区间变窄。随着土层深度比h/L的减小，有限深度土层中摩擦桩的Fc计算值将减小。

图8 有限深度地基摩擦桩竖向抗压刚度比FcFig.8 Vertical Compressive Stiffness Ratio Fc of Friction Piles in Finite Depth Foundation

图9 为土层深度比h/L=1 情况下的Fc值，即桩底位于刚性基岩顶面的情况。与半无限土体或有限均质土层中摩擦桩Fc值相比，计算的端承桩Fc值较小。桩端为坚硬岩层中时Fc值随桩间距比增加而减小，这与在半无限土或有限均质土层中摩擦桩的趋势相同。但是，端承桩的Fc值随桩土刚度比减小而增加，与摩擦桩计算结果相反。此外，Fc值随着桩长径比增加而增加。

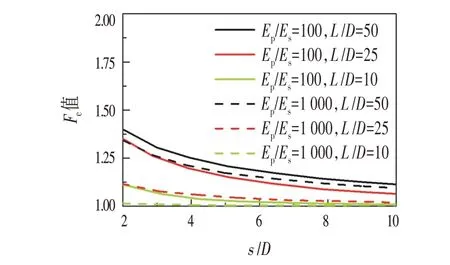
图9 底部嵌岩端承桩竖向抗压刚度比FcFig.9 Vertical Compressive Stiffness Ratio Fc of Bottom Rock Socketed End Bearing Pile

4 结论

本文建立了基于弹性理论法的抗拔单桩计算模型，以及考虑试桩与锚桩相互作用的群桩计算模型，讨论不同地层抗拔桩桩身变形和内力分布规律，以及锚桩静载试验中地层条件、桩间距等因素对试桩抗压刚度的影响。主要结论包括：

⑴ 桩土刚度比越大，桩-土界面摩阻力和桩身轴力曲线沿深度变化越小，相应桩身上拔位移量越大。当桩基位于软弱土层中时，其竖向抗拔能力相对最低。

⑵ 土体模量大的地层中桩侧抗拔摩阻力发挥水平最大，桩身轴力衰减最快。当桩基主要用于承担上拔荷载时，浅部土层性质对抗拔承载力起重要作用。

⑶ 当采用锚桩法进行单桩抗压静载试验时，试桩、锚桩与地基相互作用，导致单桩抗压刚度比真实情况偏大，考虑上述原因对静载试验结果修正，能得到与实际情况更为接近的试桩曲线。