基于扩展卡尔曼滤波算法的磷酸铁锂电池荷电状态估计*
2023-12-05韦仲爽侯巍赵彦郑寿森付青
韦仲爽, 侯巍, 赵彦, 郑寿森, 付青
1.中山大学物理学院,广东 广州 510275
2.安徽南瑞继远电网技术有限公司,安徽 合肥 230088
3.珠海银河耐吉科技有限公司,广东 珠海 519085
2020 年9 月,我国明确提出了2030 年“碳达峰”以及2060 年“碳中和”的目标。其中,重要举措就是实现燃油汽车向电动汽车的转变。电动汽车的电池体系历经了铅酸电池、镍镉电池、镍氢电池、锂离子电池四代。其中,锂离子电池是比能量密度与能量效率最高的二次电池体系(贺林等,2021),具有开路电压高、自放电率小、循环寿命长、无记忆效应、环境友好等特点。
电池管理系统(BMS,battery management system)的作用是对电池状态、能量控制管理、电池信息等进行监控(谭晓军,2021)。其中,荷电状态是最基本的参数。SoC不是直接测量量,只能通过开路电压法、安时积分法、神经网络法和卡尔曼滤波法等估算得到。刘海东等(2022)提出了一种离线式锂离子电池开路电压快速估计方法;高进等(2022)使用开路电压法估计初始荷电状态,在恒流放电末期利用负载电压法在线实时修正安时积分法SoC 的累计误差;刘昊天(2020)提出一种CNN-GRU 神经网络估算方法,对电池的SoC 进行了估算;张连德(2018)通过电池的电化学阻抗谱分析,对三元锂电池的SoC 进行了估算;王浩(2022)提出考虑电池迟滞特性的自适应遗忘因子递推最小二乘联合EKF 算法,实现了磷酸铁锂电池SoC在线实时联合估算。
开路电压法不适于对SoC 进行实时估计;安时积分法容易产生累积误差;神经网络法精度高,但依赖于样本数据,计算复杂;而卡尔曼滤波的估计结果只受到上一时刻的系统状态和当前时刻的观测值影响,即使初值误差很大,卡尔曼滤波也能在几次迭代之内迅速收敛到真实值附近,具有收敛快、精度高、不受初值误差影响的优点(王海龙等,2021;黄小平等,2022)。经典的卡尔曼滤波适用于线性系统,当用于非线性系统时,需要围绕滤波值将非线性函数展开成Taylor级数并略去二阶及以上项,得到一个近似的线性化模型,即扩展卡尔曼滤波方法。赵佳美(2018)对比了一阶、二阶扩展卡尔曼滤波算法对电池SoC 估计的影响;晏晓锋(2022)将自适应渐消扩展卡尔曼(AFEKF)算法应用于电池SoC 估算,提高了估算精度。本文从电池的外部电路特性出发,基于等效电路模型对电池进行建模分析,并结合扩展卡尔曼滤波算法对电池SoC进行估算。
1 电池模型的选择
电池的原理性模型主要分为电化学模型和等效电路模型两大类。电化学模型注重电池内部电化学机理,依据电池反应的本征特性建立模型,以对电池状态进行估计(张照娓等,2021),常见的电池电化学模型有 Unnewehr Universal 模型、Nerst 模型等(Chun et al., 2019)。电化学模型可以充分反映电池内部的电极特性、电解液浓度变化等特征,但参数辨识十分复杂,计算量极大,且不便于进行电池外部特性的电路分析(马骁,2020)。等效电路模型注重描述电池的外部电学特性,利用电容、电阻等元件搭建其电路网络,通过分析电路来分析电池在不同条件下的响应。比较常用的电路模型有Rint模型(Nemes et al.,2019),Thevenin 模型,PNGV 模型(Zhang et al.,2017)。等效电路模型的特点如表1所示。

表1 不同等效电路模型的特点Table 1 Characteristics of different equivalent circuit models
Rint模型使用一个欧姆内阻来模拟电压的瞬态响应。Thevenin 模型在Rint模型的基础上,增加了RC 并联网络,用以描述电池内部的电化学极化和浓差极化,使电池的动静态特性得到体现,模型精度显著提高(凤良,2021)。PNGV 模型在Thevenin 模型的基础上新串联一个电容,用以表征开路电压与负载电流的时间积分关系(贾玉健等,2011)。因此,PNGV 模型对电池动态响应的描述更精确,但在恒流工况下容易产生误差。本实验基于二阶Thevenin 模型对电池系统进行建模分析。二阶Thevenin模型如图1所示。

图1 二阶Thevenin等效电路模型Fig.1 The second-order Thevenin equivalent circuit model
2 模型参数识别
2.1 电池特性测试
实验使用的是48173125-100Ah 型可充电磷酸铁锂电池,电池额定容量为100 Ah。测试设备是新威CT4001 高性能电池检测系统(5V1000A)。电池的标准充电流程为恒流恒压充电,先以0.5 C 倍率恒流充电至截止电压为3.65 V,再以3.65 V 恒压充电至截止电流0.05 C。
以电池的放电过程为研究目标,对本批次的锂离子电池进行分组。三个电池为一组,每组电池单体的编号为1 号、2 号、3 号,以标准充电流程充满电,再以20、40、60 A 做恒流放电测试,测试锂离子电池容量,结果如表2所示。
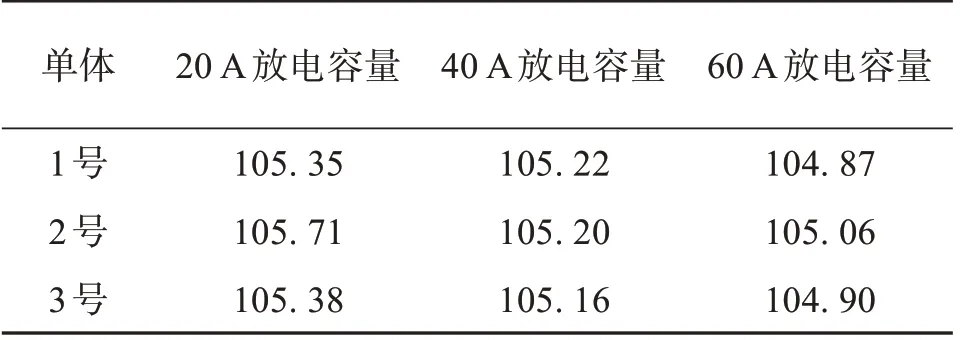
表2 不同放电倍率下的锂离子电池放电容量Table 2 Capacity of lithium-ion batteries at different discharge rates Ah
从表2可知,三支锂离子电池的平均容量均在105 Ah 左右。为使后面的实验与锂离子电池的实际情况更贴合,将电池的额定容量更正为105 Ah。图2是三支锂离子电池单体在40 A恒流放电工况下的放电曲线。图2中,三支锂离子电池单体的放电时间均在160 min 左右,放电平台在3.0~3.3 V,且具有很强的一致性。在放电初始时刻,电池的端电压均向下突降;放电末期,电池的端电压再次急剧下降,直至截止电压2.5 V。

图2 40 A恒流放电工况下的放电曲线Fig.2 Discharge curve under constant discharge condition of 40 A
2.2 模型参数识别
根据基尔霍夫定律,图1 所示的二阶Thevenin等效电路模型可表述为
其中Ut表示t时刻锂离子电池的端电压;OCV表示当前SoC 处锂离子电池的开路电压;R0表示锂离子电池的欧姆内阻;U1和U2分别表示两个RC回路的电压,用以描述锂离子电池内部的极化反应。
为了提高不同SoC 点处的模型参数的准确性,本文将采用变参数的二阶Thevenin 模型,即模型参数随着电池SoC而变化。因此,需要对不同SoC处的OCV,R0,R1,R2,C1,C2进行如下识别:
(1)对电池放电,使SoC 发生固定变化,通过静置测量OCV;
(2)分析电池电压的瞬态响应,识别等效内阻R0;
(3)分析电池电压的回弹特性, 识别R1,R2,C1,C2。
基于以上分析,利用《FreedomCar 功率辅助型电池测试手册》中的混合脉冲功率特性测试方法对电池进行测试。HPPC 测试通过在特殊的SoC点对电池进行10 s 的放电脉冲、充电脉冲实验和40 s 的静置,以获得电压的瞬态响应及回弹特性。放电脉冲电流选用产品规格书中所允许的最大电流;充电脉冲电流设置为放电脉冲电流的0.75 倍作为能量补偿。即在SoC >20%时,允许最大放电脉冲电流为200 A,对应的充电脉冲电流为150 A;在SoC ≤20%,允许最大放电脉冲电流为100 A,对应的充电脉冲电流为75 A。
为了使HPPC 脉冲测试与特定的SoC 点相对应,实验中先按标准充电流程对电池充满电,此时电池的SoC 为100%。之后以1 C 放电6 min,使SoC 下降10%。每次SoC 发生改变后,立刻进行2 h 静置,读取此时的开路电压。本实验对SoC 为90%, 80%, 70%, 60%, 50%, 40%, 30%,20%,10%的点进行HPPC 实验,其步骤为:(1)标准充电流程充满,静置2 h;(2)1 C 放电6 min,静置2 h;(3)单个HPPC 脉冲测试;(4)重复步骤2~3,重复次数为9 次;(5)0.5 C 放电至截止电压2.5 V。每次工步(2)结束后,可以测得电池的开路电压,如图3所示。

图3 OCV-SoC关系图Fig.3 OCV-SoC curve
得到OCV 和SoC 之间的关系后,利用MATLAB的cftool工具箱,对其进行七阶多项式拟合得
据公式(2)可近似表达任意SoC 点处锂离子电池的开路电压OCV。为了识别其他的参数,对SoC=90%处的HPPC 测试数据进行分析。该HPPC测试过程如图4所示。
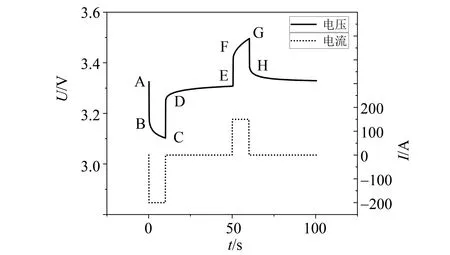
图4 SoC=90%处的HPPC测试Fig.4 The HPPC test at SoC=90%
在图4 中,电池的端电压分别出现了四次突变,分别是AB 段、CD 段、EF 段和GH 段,这四处突变都与电池的欧姆内阻相关。《FreedomCar 功率辅助型电池测试手册》中,欧姆内阻为
其中UC,UD,UG,UH分别为该点处的端电压,Idis为放电脉冲电流,Icha为充电脉冲电流,因为内阻不可能为负,所以公式中Idis和Icha都取绝对值。
观察图4 中的DE 段,此时没有电流,端电压的变化是电池内部极化反应的外部表现。将DE 段看作是系统的零输入响应,用二阶Thevenin 等效电路模型的两个RC 回路来模拟其内部的极化反应。结合公式(1),DE 段的端电压可表示为
利用MATLAB 的cftool 工具箱,对DE 段的响应进行自定义函数拟合得
通过对比公式(4)和(5),可得
电流I取放电脉冲电流的绝对值。通过分析,可得不同SoC点处的R0,R1,R2,C1,C2的值,如表3 所示。令τ1=R1C1,τ2=R2C2分别为两个RC回路的时间常数,其结果如表4所示。
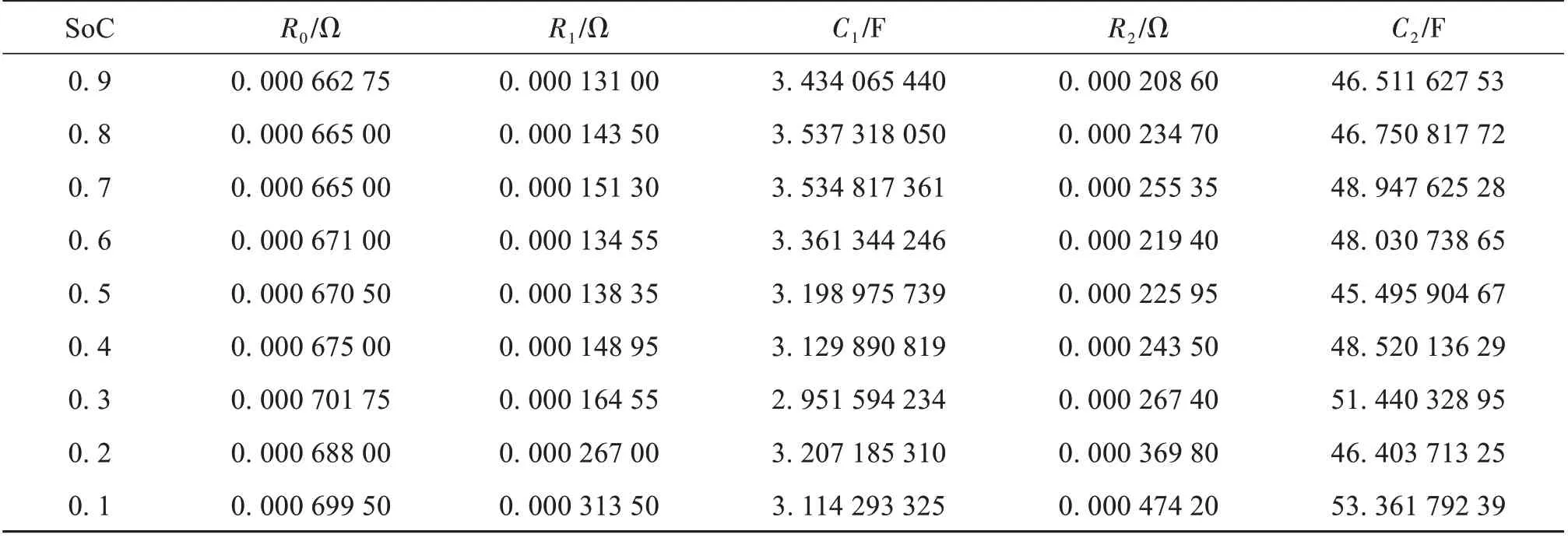
表3 参数辨识结果Table 3 Results of parameter identification
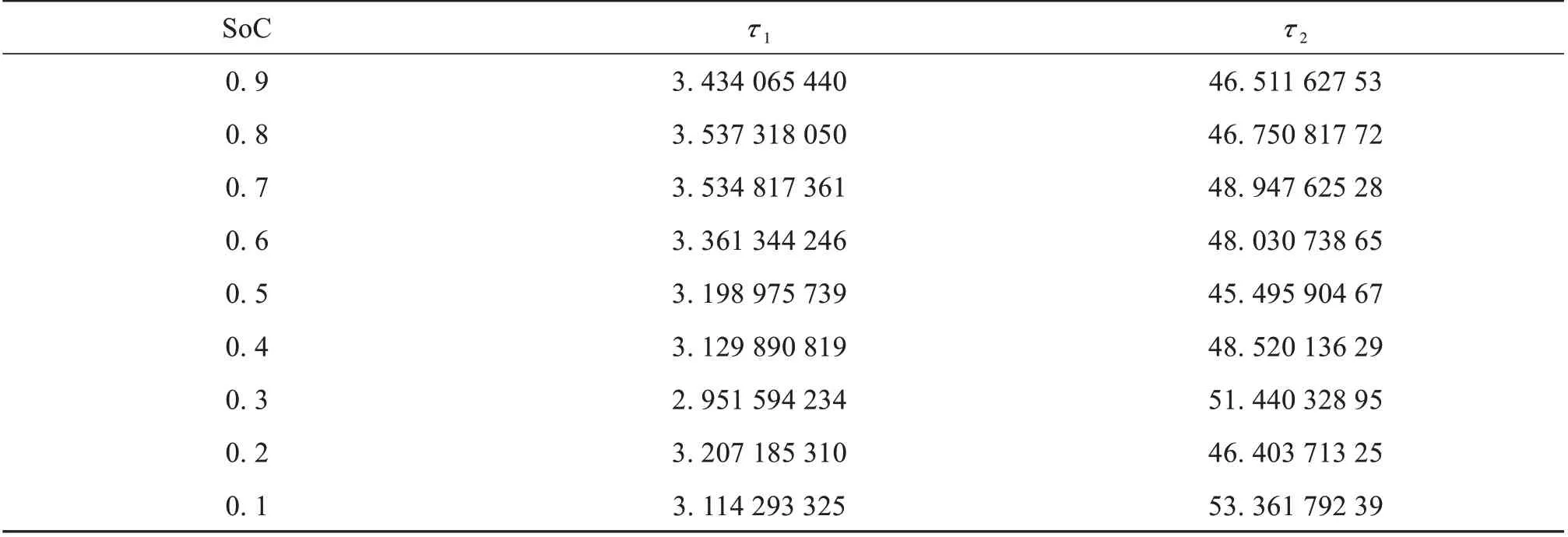
表4 τ1和τ2辨识结果Table 4 Identification results of τ1, τ2
3 扩展卡尔曼滤波
3.1 卡尔曼滤波步骤
根据建立的二阶Thevenin 等效电路和公式(1),可以列出模型的状态空间方程:
其中x为系统的状态变量,A为状态矩阵,B为输入矩阵,u表示系统的输入,w为系统的过程噪声,且有P(w)~(0,Q);z为系统的测量结果,H为观测矩阵,v为测量噪声,且P(v)~(0,R)。根据状态空间方程,使用卡尔曼滤波可对系统的状态(k时刻的状态变量)进行估计。具体步骤如下:
卡尔曼滤波先是忽略了系统的过程噪声,通过前一时刻的状态xk-1和输入uk-1计算得到一个先验估计值;然后通过分析过程噪声的协方差矩阵Q和观测噪声的协方差矩阵R,判断先验估计值和观测值zk哪一个值更值得信任。因此卡尔曼增益Kk的范围应该在[0,1]之内,当Kk=0时,则完全信任先验估计值;当Kk=1 时,则完全信任观测值zk.卡尔曼滤波的流程如图5 所示。
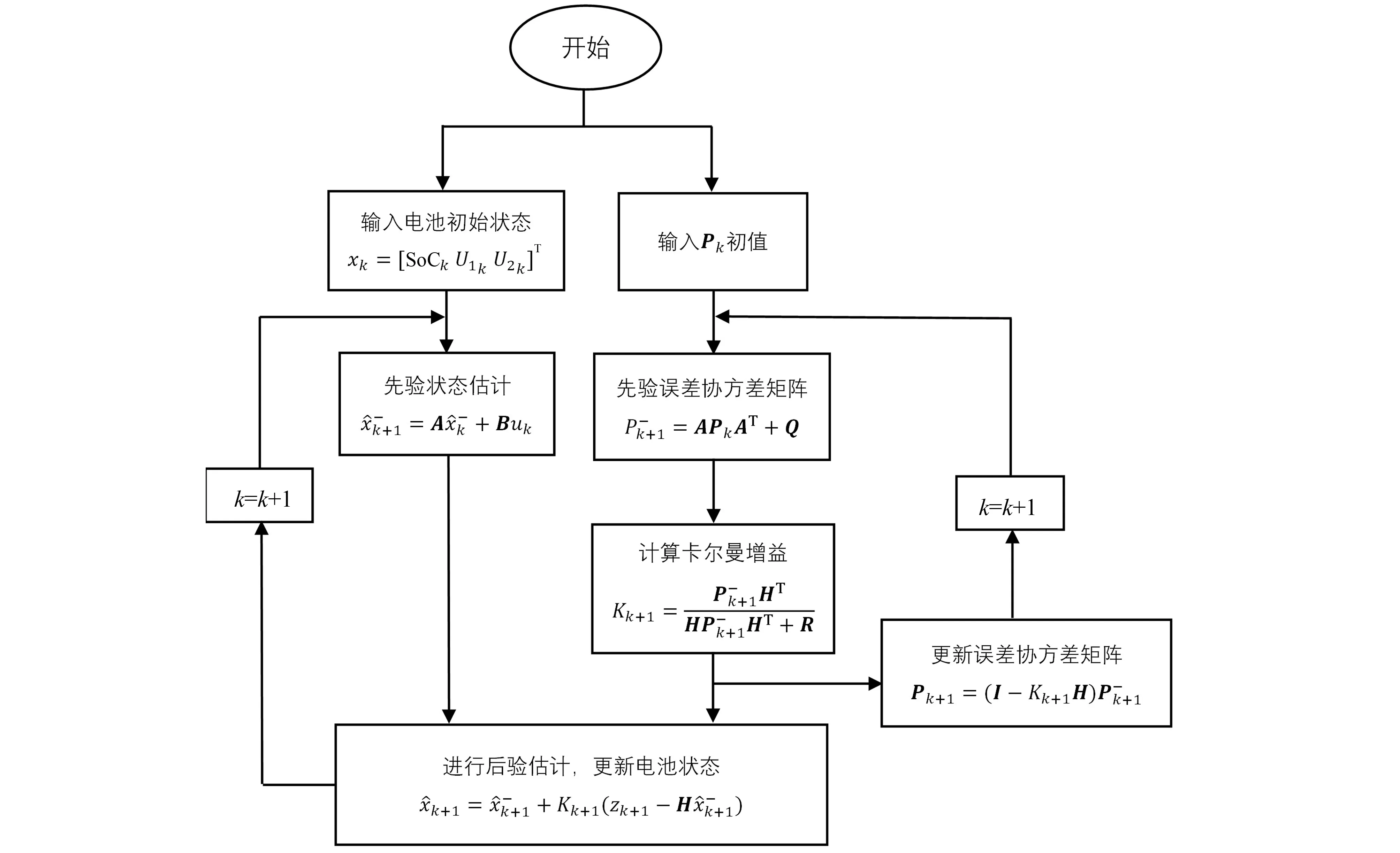
图5 卡尔曼滤波流程Fig.5 Flow chart of Kalman filter
3.2 系统状态空间方程
公式(1)给出了二阶Thevenin 模型的电路方程。将电流I定为输入,将端电压Ut定为观测量,并选取x=[SoCU1U2]T为系统的状态变量,其中SoC 为待估算的量,列出状态方程和输出方程:
SoC的变化可以表示为
其中SoC(t)表示t时刻的SoC 值;SoC(to)表示初始时刻的SoC 值,通常由初始条件给出;η表示库伦效率,I(t)表示瞬时充放电电流,以充电为正电流,放电为负电流;Cn表示电池的额定容量。
公式(2)表明OCV与SoC为非线性关系,因此需要将状态空间方程进行泰勒展开处理后再运用经典卡尔曼方法进行估算。对方程进行离散化处理,得到离散后的状态方程为
为系统的状态矩阵;
为系统的控制矩阵;ik为k时刻的电流,是系统的输入,规定放电为负,充电为正;wk为系统的过程噪声,且P(wk)~(0,Q),即wk的期望为0,协方差矩阵为Q。将前面参数识别得到的参数值代入就可以确定具体时刻的A,B矩阵的值。
同理,可以得到离散化后的系统的观测方程:
公式(11)和(12)即为二阶Thevenin 等效电路分析模型离散化后的状态空间方程。将不同SoC 处的参数OCV,R0,R1,R2,C1,C2代入,便可以确定各个矩阵的值。变参数二阶Thevenin 模型与扩展卡尔曼滤波相结合的SoC 估算系统,如图6所示。
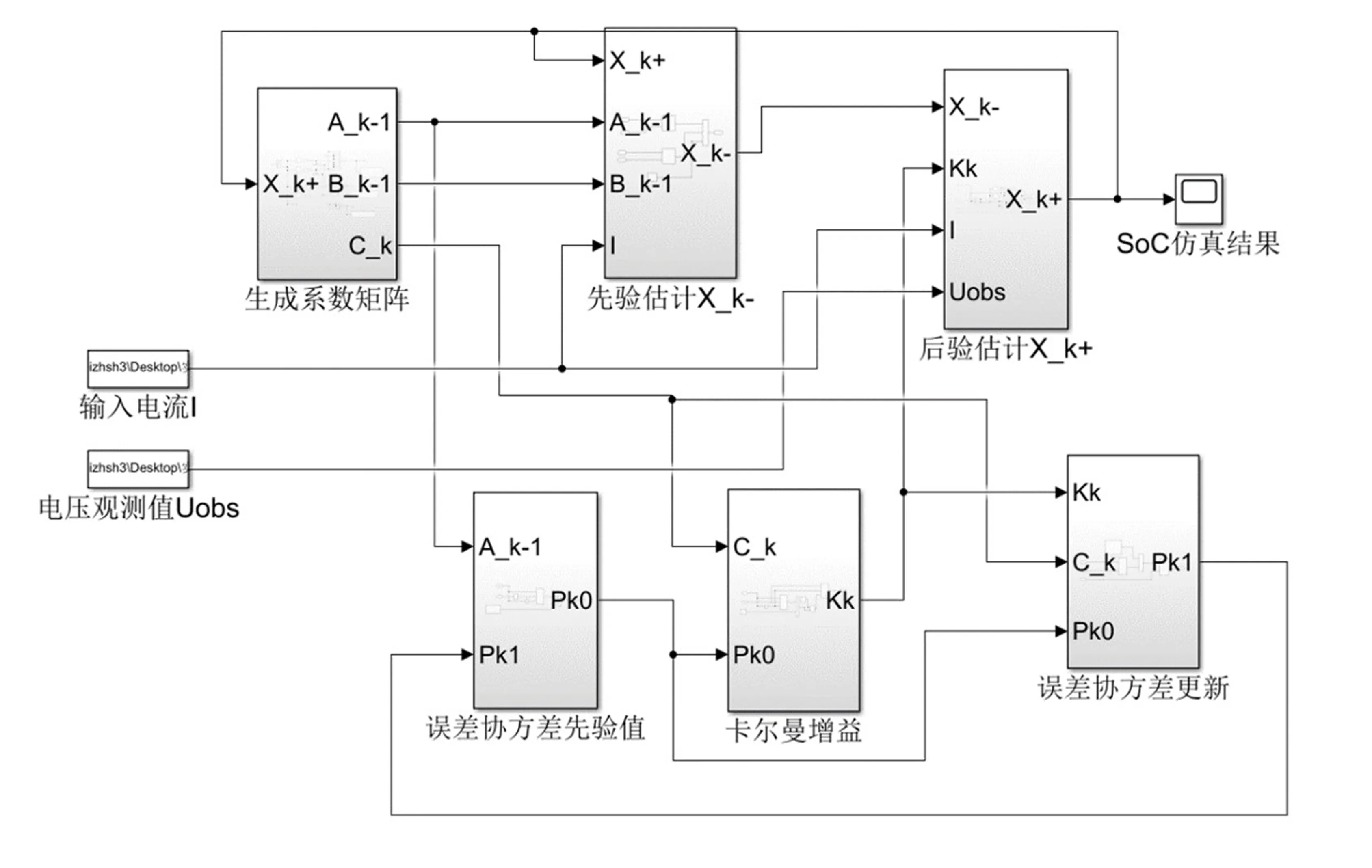
图6 变参数二阶Thevenin模型的EKF估算系统Fig.6 Variable parameter second-order Thevenin model EKF estimation system
4 仿真结果分析
通过对SoC 初值及输入电流进行设定,可以使安时积分法具有极高的准确性。因此,以安时积分法计算得到的电池SoC 值为标准值,验证仿真结果的准确性。结果如图7所示。

图7 安时积分法仿真Fig.7 Simulation of Ampere-hour integration method
4.1 恒流放电工况的仿真结果
取20、60 、100 A 的放电数据为模型的输入,得到的EKF 估计值如图8 所示。定义误差=SoCEKF值- SoC标准值,则20、60、100 A 恒流放电工况的仿真误差如图9所示。

图8 20、60和100 A放电仿真结果Fig.8 Simulation results of discharge at 20 , 60 and 100 A
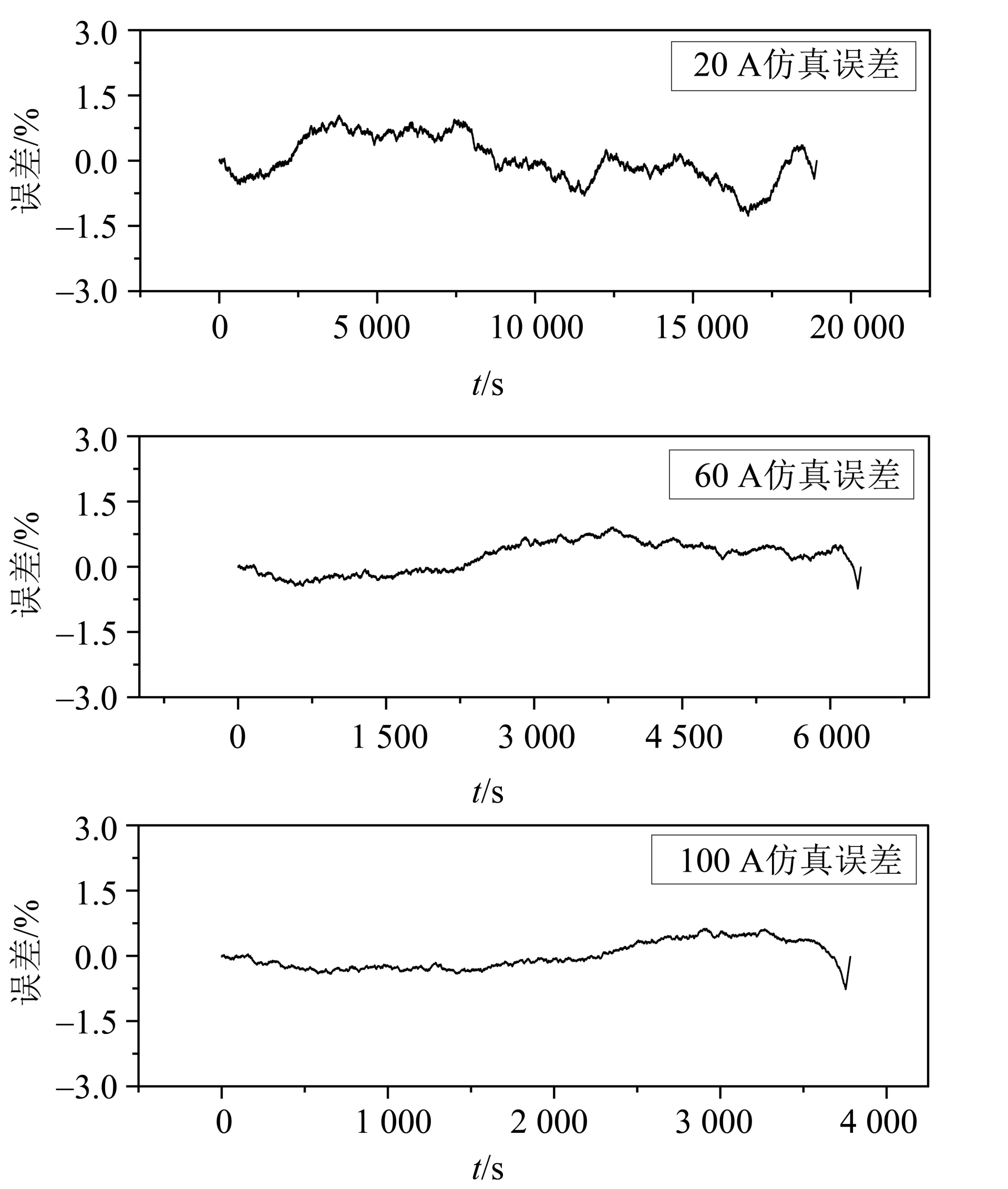
图9 恒流放电工况的仿真误差Fig.9 Simulation error under constant current discharge condition
通过仿真对比结果图和误差图可以看出,EKF得到的SoC 估算值与标准值相比,最大误差不超过1.5%SoC,是一个高精度的估算结果。在SoC≤20%时,误差有稍微变大。但对于恒流放电工况而言,EKF 估算值在整个放电过程都能与标准值高度一致,验证了模型的准确性。
4.2 循环放电工况的仿真结果
为了进一步验证模型的准确性,根据GB/T 31484-2015 中的电动商用车用能量型蓄电池循环放电工况试验对模型进行测试。实验步骤和电流示意图如表5和图10所示。

图10 循环放电工况电流示意图Fig.10 The current in the cycle discharge condition

表5 蓄电池循环放电工况Table 5 Cycle discharge condition of energy storage battery
实验过程中让锂离子电池循环进行主放电工况测试,每一个循环SoC 的变化为-0.572%,故而循环次数为= 174.8 次。同样,将放电工况的电流数据输入到EKF 估算系统和安时积分法估算系统中,仿真结果和误差如图11-12所示。

图11 循环放电工况的仿真结果Fig.11 Simulation results of cyclic discharge condition

图12 循环放电工况的估算误差Fig.12 Estimation error of cyclic discharge condition
从图11-12 可知,SoC >20%时,EKF 估算得到的仿真值与标准值是非常接近的,误差基本保持在1%以内。但当SoC≤20%时,仿真值开始偏离标准值,在放电末期的误差超过了2%且
(1)通过HPPC 实验进行参数识别时,每隔10%SoC 会进行一次脉冲实验。在SoC >20%时,电池采用的放电脉冲是200 A;在SoC≤20%时,由于电池规格书的说明,最大放电脉冲电流只能取100 A,脉冲电流小,模型参数的识别误差变大,导致模型精度有所下降。
(2)通过电池的放电曲线可以看出,在SoC≤20%时,电池的端电压的变化非常剧烈,从放电平台的3.2 V 左右迅速下降到截止电压2.5 V。相应地,脉冲实验的间隔应该缩小,以捕获更多的模型特征参数。
为了再进一步分析误差,将仿真过程中计算得到的电池端电压与实际测量得到的端电压进行对比,二者的误差如图13所示。
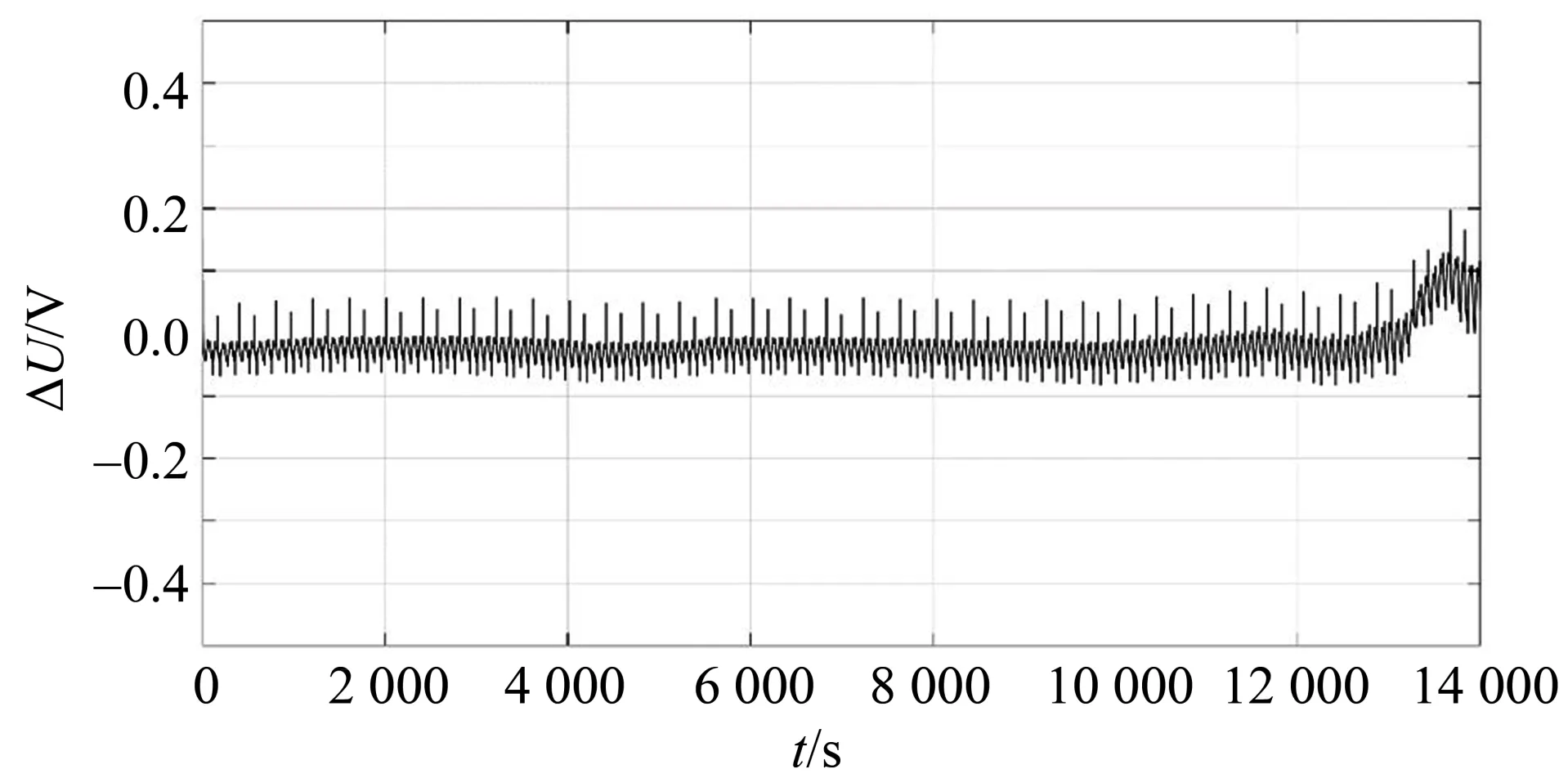
图13 循环放电工况的端电压误差Fig.13 Simulation error of terminal voltage in cyclic discharge condition
可以发现,在SoC >20%的阶段,端电压的仿真误差非常小(在±0.1 V 之间),说明模型极准确地模拟了端电压的变化。当SoC≤20%时,电压误差开始增大,达到了0.2 V。对卡尔曼滤波而言,仿真电压是一个先验估计值,卡尔曼增益需要在仿真值与实测值之间进行权衡,由于模型在SoC≤20 时精度不够,影响了仿真值的精度,从而影响了SoC的计算。
5 结 论
本文基于二阶Thevenin 电路模型,建立了锂离子电池的分析模型,并通过HPPC 测试对不同SoC 处的模型参数OCV,R0,R1,R2,C1,C2进行了识别。基于MATLAB/Simulink 平台,搭建了变参数二阶Thevenin 模型与扩展卡尔曼滤波相结合的SoC 估算系统,并对锂离子电池恒流放电工况及电动商用车用能量型蓄电池主放电工况进行了仿真。仿真结果表明,变参数SoC 估算系统的估算误差与理想状态下的安时积分法计算的标准值相比,误差不超过2.5%,说明模型能够较好地模拟锂离子电池的动静态特性,为电池管理系统传递准确的状态信息。
