20Cr2Ni4A钢的高温热变形行为及热加工图

周少荣 ,吴晓东 ,黄寅舜 ,张肖佩佩 ,王忠英

(1.江苏大学材料科学与工程学院,镇江 212013;2.钢铁研究总院华东分院,淮安 223000)

0 引言

齿轮在机械设备的传动过程中起着十分重要的作用,经常在高速重载的复杂工况下工作,因此其材料应具备硬度高、断裂韧性优异、疲劳强度高等特点。20Cr2Ni4A钢是一种具有良好淬透性和高强韧性的合金渗碳钢,被广泛用于制作重载车辆的传动齿轮[1-2]。在齿轮的制造过程中,热塑性成形是基础工序,其工艺参数选择得当可细化齿轮钢的奥氏体晶粒,从而提高齿轮的强韧性和使用寿命,反之则可能形成局部变形、绝热剪切带、楔裂等成形缺陷,缩短齿轮使用寿命。探究20Cr2Ni4A 钢在热变形过程中的组织和性能变化规律,可以为其热塑性成形工艺的制定提供依据[3]。目前,国内外对20Cr2Ni4A 钢的研究集中在钢种成分设计及后续的表面硬化处理工艺上,对其热变形行为和热加工图的研究较少。因此,作者采用热模拟试验机对20Cr2Ni4A钢进行热压缩变形试验,对压缩真应力-真应变曲线进行摩擦修正,消除热压缩过程中的端面摩擦效应,在此基础上构建了Arrhenius本构方程;采用建立的Arrhenius本构方程表征了该钢流变应力与变形参数的关系,建立了基于动态材料模型(DMM)的热加工图,并获得了合理的热加工工艺参数。

1 试样制备与试验方法

试验材料为20Cr2Ni4A热轧钢棒,由西宁特殊钢股份有限公司提供,化学成分见表1。

表1 20Cr2Ni4A钢的化学成分Table 1 Chemical composition of 20Cr2Ni4A steel

在热轧钢棒上取尺寸为ϕ8 mm×12 mm 的试样,在其两端用钽片涂上石墨润滑剂,以减少压缩过程中端面与压头的摩擦。采用Gleeble-3500型热模拟试验机进行单道次压缩试验:在真空环境下以10 ℃·s-1的升温速率将试样加热到1 200 ℃,保温3 min使其组织完全奥氏体化,再以10 ℃·s-1的冷却速率降温到不同变形温度(800,850,900,950,1 000,1 050 ℃),保温30 s以消除温度梯度,然后在应变速率分别为0.01,0.1,1,5 s-1下进行压缩变形,试样高度方向的压缩变形量为55%,真应变达0.8,压缩试验结束后立即水淬。

将试样沿压缩方向线切割成类半圆柱体,将截面打磨、抛光,使用由4 g苦味酸和100 g蒸馏水配制成的溶液在55 ℃下腐蚀2～3 min,采用Zeiss Observer.Z1m 型光学显微镜观察显微组织。

2 结果与讨论

2.1 真应力-真应变曲线

在热压缩试验中,试样因与压头之间存在摩擦作用,在压缩变形过程中会产生不均匀变形,导致流变应力实测值大于真实值。因此,需要对实测流变应力进行摩擦修正[4-6],计算公式如下:

式中:σf为修正后的流变应力;σ为实测流变应力;ε为实测应变;f为摩擦修正因子;Δr为压缩后试样最大半径和最小半径之差;Δh为压缩前后试样的高度差;r0,h0分别为试样初始半径和初始高度;r,h分别为压缩后试样平均半径和平均高度;b为鼓肚参数;rm,rt为压缩后试样的最大半径和最小半径。

由图1可见:经摩擦修正后的真应力-真应变曲线与实测曲线的整体变化趋势基本相同,但修正后的真应力均小于实测真应力,并且随着应变的增大,二者差值增大。这是因为在热压缩过程中,随着变形程度的增大,试样与压头的接触面积不断增大,摩擦效应逐渐显著,产生的误差增大。由此可见,采用上述摩擦修正方法可以降低试验中摩擦效应造成的误差,经摩擦修正后的真应力-真应变曲线更能真实地反映20Cr2Ni4A钢的热变形流变行为。

图1 不同条件压缩时试验钢实测和摩擦修正后的真应变-真应力曲线Fig.1 True strain-true stress curves of test steel measured and after frictional modification during compression under different conditions

在较低温度变形时试验钢的动态软化作用明显小于加工硬化作用,其真应力-真应变曲线呈现明显的加工硬化特征;在较高温度下,原子热振动加剧,位错易于滑移,加工硬化程度降低,同时动态软化作用明显加强,因此试验钢的流变应力降低,峰值应变减小。在低应变速率(0.01,0.1 s-1)下试验钢变形较缓,为再结晶晶粒的形核长大提供了充足的时间,有利于动态再结晶的进行,曲线表现为动态再结晶型,且曲线的动态再结晶特征随着变形温度的升高愈发明显;而在高应变速率(1,5 s-1)下试验钢变形较快,其内部位错的大量增殖会导致加工硬化作用增强,晶粒无法充分形核长大,不利于动态再结晶过程的进行,流变应力虽增加,但增长速率随着变形温度的升高逐渐放缓,逐渐稳定在一个范围内,曲线表现为动态回复型。综上可知,试验钢在850～1 050 ℃动态软化作用明显,尤其是在低应变速率下。

2.2 本构模型

Arrhenius方程可用于描述流变应力与应变速率和变形温度之间的关系,其表达式[7-10]为

当温度一定时,式(6)和式(7)两边取自然对数,将不同应变速率及对应的摩擦修正后的峰值应力代入方程,并进行线性拟合,拟合曲线如图2所示,其斜率分别为n1和β的值,即:

图2 应变速率与峰值应力拟合曲线Fig.2 Fitting curves of strain rate vs peak stress

由此得到n1=9.131,β=0.067 8 MPa-1,平均相关系数分别为0.983和0.998。由β和n1得到α=0.007 425 MPa-1。

分别在温度一定和应变速率一定的条件下对式(8)两边取自然对数,代入应变速率或温度以及摩擦修正后的峰值应力并进行线性拟合,拟合曲线如图3所示,其斜率分别为n值和Q/(nR)值,即:

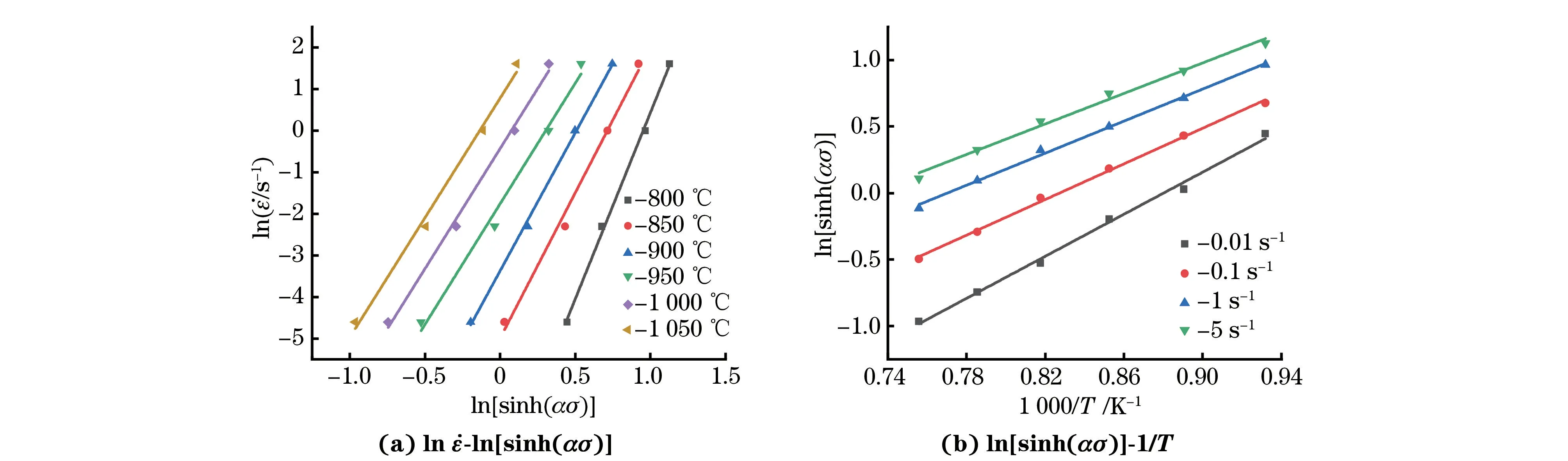
图3 ln-ln[sinh(ασ)]和ln[sinh(ασ)]-1/T 拟合曲线Fig.3 Fitting curves of ln -ln[sinh(ασ)]and ln[sinh(ασ)]-1/T

由拟合结果可得到n=6.657,拟合度为0.992;由于Q/(nR)=6.591 19,那么代入n就可以得到Q=364.770 566 kJ·mol-1,相关系数为0.995。Z参数(Zener-Hollomon参数)是用以表征变形温度和应变速率的函数,其定义式如下:

通过Z参数可以建立精度较高的流变应力本构模型,对金属材料的高温流变行为进行有效预测[11]。

将式(13)取自然对数,可得

采用修正后的数据对lnZ和ln[sinh(ασ)]进行线性拟合,结果如图4所示。由截距得到lnA值为34.188 91,相关系数为0.987 61,则A=7.05×1014,n值修正为6.517 79。试验钢的Z参数表达式如下:

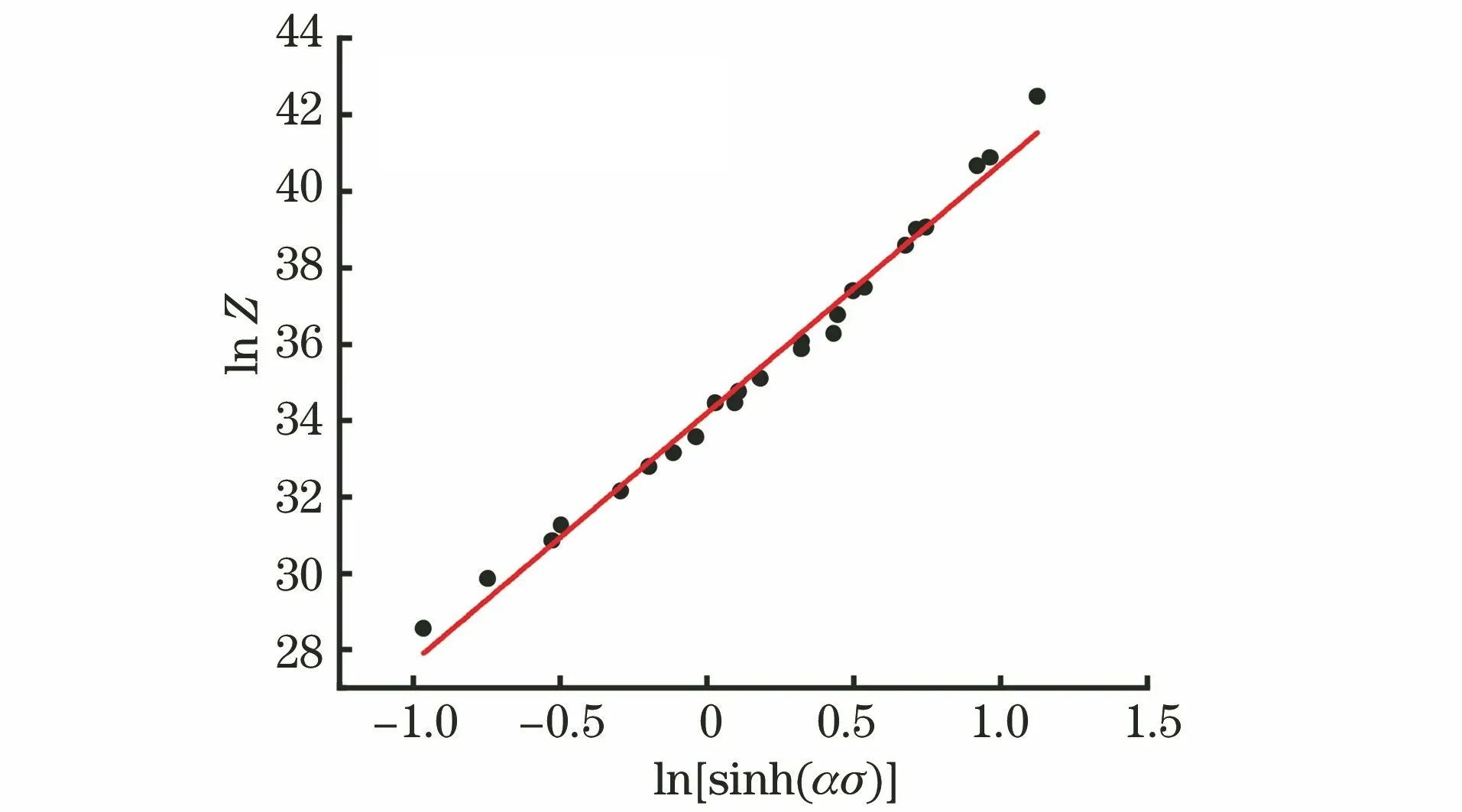
图4 ln[sinh(ασ)]-ln Z 线性拟合曲线Fig.4 Linear fitting curve of ln[sinh(ασ)]-ln Z

将各项参数代入式(8),得到20Cr2Ni4A 钢的热变形本构方程为

将Z参数代入式(15),变形得到:

将不同的应变速率、变形温度代入式(17),即可得到不同热变形参数下峰值应力的预测值。由图5可见,峰值应力预测值与摩擦修正后的峰值应力(真实峰值应力)较吻合,相关系数达0.986 02,平均相对误差绝对值为3.44%,多数试验条件下的相对误差低于5%。综上可知,构建的20Cr2Ni4A 钢的本构模型能够较为准确地计算流变应力,表征其热变形行为,为其热加工过程提供理论指导。

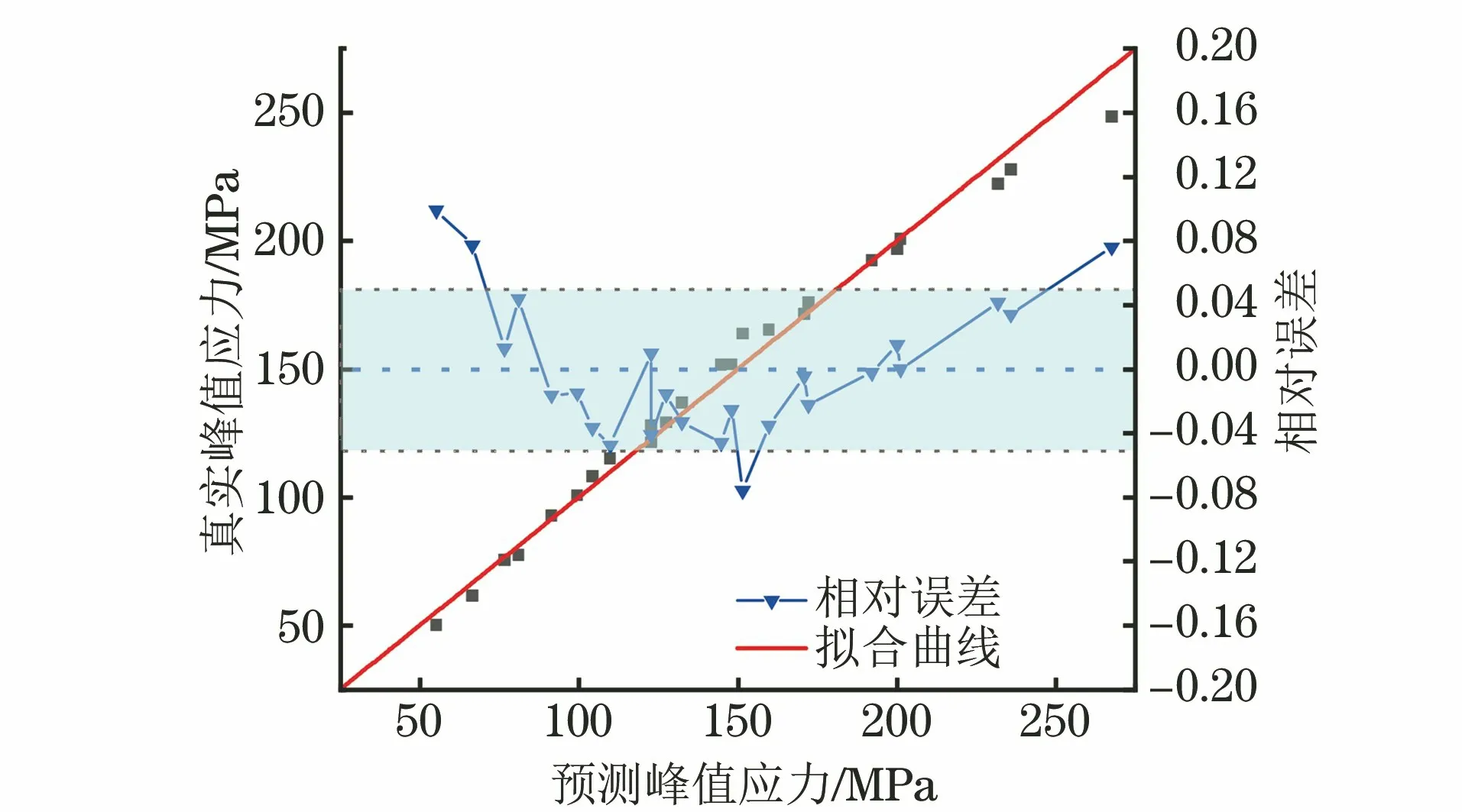
图5 峰值应力预测值与真实值的关系及相对误差Fig.5 Relationship and relative error between predicted and ture values of peak stresses

2.3 热加工图

根据动态材料模型(DMM)理论,材料在热加工过程中所获得的能量P以2种方式进行耗散:一是通过材料发生塑性变形而耗散,这部分能量以功率耗散量G来表示;二是通过材料变形时内部组织发生演变而耗散,这部分能量以耗散协量J来表示[12-14]。

在一定应变条件下,引入应变速率敏感指数m来描述上述2种能量耗散方式的比例:

在一定变形温度和应变下,J的表达式为

金属材料发生热变形时进行显微组织演变的功率耗散效率可用功率耗散因子η表示,表达式如下:

PRASAD等[15]引入流变失稳参数ξ,推导出材料的流变失稳判断依据,如下:

热加工图是根据动态材料模型将功率耗散图和流变失稳图共同叠加构成的,反映了材料热变形参数与显微组织演变之间的关系[16-17]。图6是根据修正后的流变曲线所建立的热加工图,图中阴影部分为失稳区,等高线数值为功率耗散因子。由图6可知:随着应变增加,功率耗散效率峰值虽维持在低应变速率区域,但逐渐向低温区移动;当应变达到0.6时,峰值趋于稳定,稳定区域在变形温度850～950 ℃、应变速率0.01 s-1处,且峰值均大于0.4。通常在材料热加工时,功率耗散因子较高区域的热加工性能更好;但并不是功率耗散因子越高材料的热加工性就一定越好,因为热变形过程中的各类缺陷如内部开裂或者楔形开裂都会耗散能量,导致较高的功率耗散因子。因此,还需要对相应的失稳图进行分析。

图6 不同应变下试验钢的热加工图Fig.6 Hot processing map of test steel at different strains

在热加工初期(应变为0.2),失稳区分散为3个区域,随着应变增加,失稳区逐渐扩大,最终形成一个连续失稳区。失稳区域主要存在于低温区(800～850 ℃、应变速率0.5～5 s-1)处,中温区(850～925 ℃、应变速率0.02～1 s-1)处,高温区(925～1 050 ℃、应变速率1～5 s-1)处。在失稳区进行热加工可能会形成楔形开裂、局部流变失稳、绝热剪切带等缺陷,工艺参数的选择应尽量避开该区域。因此,综合功率耗散图和流变失稳图分析,合理的热加工参数分别为变形温度875～925 ℃、应变速率0.01～0.02 s-1和变形温度925～1 050 ℃、应变速率0.01～1 s-1。

2.4 显微组织

由图7 可见:在变形温度800 ℃、应变速率1 s-1条件下变形后,试验钢晶粒垂直于压缩方向被拉长,晶界被拉长形成流线,在该条件下变形时试验钢处在低温流变失稳区,出现局部塑性流动特征;在变形温度900 ℃、应变速率1 s-1条件下变形后,试验钢中出现了再结晶组织,晶粒在高应变速率下被拉长,晶界呈锯齿状,在该条件下变形时试验钢处在中温流变失稳区,再结晶晶粒在晶界处形核且数量不断增多;在变形温度1 000 ℃、应变速率1 s-1条件下变形时,试验钢动态软化加剧,变形后组织中的变形晶粒减少,再结晶晶粒增多且尺寸明显增大,但是晶粒大小不均匀,出现混晶;在变形温度800 ℃、应变速率0.01 s-1条件下变形后,试验钢的晶粒明显拉长,但与应变速率1 s-1下相比,因变形时间较长,位错间的滑移湮灭使试验钢发生动态回复,在变形晶粒晶界处形成大量等轴亚晶进而诱发动态再结晶;在变形温度900 ℃、应变速率0.01 s-1变形条件下,功率耗散因子达到峰值,试验钢的动态软化演变过程最强,变形后的动态再结晶晶粒尺寸小且均匀;在变形温度1 000 ℃、应变速率0.01 s-1变形条件下,试验钢的动态再结晶晶粒相比于变形温度900 ℃下长大显著,但晶粒仍较均匀。由此可见,在变形温度不低于900 ℃、应变速率在0.01～1 s-1条件下变形后,试验钢可以得到均匀细小的等轴再结晶晶粒。这与热加工图确定的20Cr2Ni4A 钢合理的热加工参数范围基本吻合。

3 结论

(1) 在热压缩过程中压头与20Cr2Ni4A钢试样之间产生的摩擦效应对流变应力有显著影响,经摩擦修正后的流变应力明显低于实测值,且随着应变的增加,摩擦修正前后的应力差值逐渐变大;摩擦修正后的流变曲线分为加工硬化型(变形温度800 ℃、应变速率0.01～0.1 s-1和变形温度800～850 ℃、应变速率1～5 s-1)、动态回复型(变形温度900～1 050 ℃,应变速率1～5 s-1)、动态再结晶型(变形温度850～1 050 ℃、变形速率0.01～0.1 s-1),试验钢在低应变速率0.01～0.1s-1、变形温度850～1 050 ℃下变形时均发生较明显的动态再结晶。

(2) 采用摩擦修正后的流变应力数据,基于Arrhenius方程建立试验钢的热变形本构模型,预测得到的峰值应力与修正后的真实值的平均相对误差绝对值在3.44%,说明该模型可以准确地对20Cr2Ni4A钢的热变形行为进行预测。

(3) 根据摩擦修正的流变曲线建立20Cr2Ni4A钢的热加工图,并结合显微组织得出最适宜的热变形工艺参数为变形温度875～925 ℃、应变速率0.01～0.02 s-1和变形温度925～1 050 ℃、应变速率0.01～1 s-1。