基于粒子群-蒙特卡罗的PDF形状控制策略

梁思敏,王玲芝,张 坤,李晨阳

(西安邮电大学 自动化学院,陕西 西安 710121)

在实际应用中,大多数控制系统会受到各种形式的随机干扰,例如由于环境变化或不确定性导致的参数变化、控制对象运动过程中的随机干扰以及测量和传感器误差等[1-3]。这些随机干扰因素使得系统极其复杂,导致使用传统的确定性控制方法难以取得良好的控制效果。为了提高控制性能,随机控制理论提供了一种通过建立数学模型描述随机干扰因素对系统产生影响的方式。因此,研究随机控制方法对实现复杂动态系统的高效控制、提高系统性能和稳定性尤为重要。

常见的随机控制方法主要是以均值和方差为控制目标,但其只能控制随机变量的一阶矩和二阶矩,不能控制更高阶矩,因此不能更准确全面地实现随机控制[4-5]。尽管风险敏感控制可以控制各阶矩的加权和,但仅通过一个风险敏感系数将性能指标的各阶矩控制到期望的形式,具有一定的难度[6]。以上均值控制、方差控制和风险敏感控制均存在控制不全面或者控制困难的问题,而解决这一问题的途径就是控制概率密度函数(Probability Density function,PDF)的形状。PDF包含了随机变量的各阶矩,可以更全面地描述随机变量的统计特征,因此控制PDF的形状就意味着随机变量的各阶矩均得到了控制[7]。

PDF形状控制的本质是设计一个控制器使得随机变量的PDF形状尽可能地与期望的PDF形状逼近。而控制器增益的求解是获得最优控制器的一个关键问题,通常采用非线性最小二乘法、共轭梯度法、遗传算法和粒子群算法等[8-11]。粒子群算法作为一种常用的优化算法,可以用于搜索函数的最小值或最大值。与遗传算法、模拟退火算法等优化算法相比,粒子群算法具有收敛速度快、参数少、算法简单等特点,被广泛应用于机器学习、数据挖掘和信号处理等领域[12-14]。蒙特卡罗方法也称统计模拟方法,是将求解问题转化为一个随机过程,并通过大量的随机抽样估算随机变量的期望值,从而得到问题的近似解。蒙特卡罗方法可以处理其他方法不能解决的复杂问题,目前已被广泛应用于物理、化学、生物和经济等领域[15-20]。

针对传统的随机控制方法不能控制随机变量的高阶矩问题,拟提出一种基于粒子群-蒙特卡罗的PDF形状控制策略。通过设计多项式形式控制器和误差平方积分目标函数,求解PDF形状控制器增益的最优值。即用粒子群算法优化控制器增益的同时,用蒙特卡罗方法计算目标函数,以期使得非线性随机系统状态变量的PDF形状与期望的PDF形状一致。

1 问题描述

假设在时刻t的一维非线性随机动态系统的状态方程为

dx(t)=[φ(x)+u(x)]dt+dε(t)

(1)

式中:x∈Rn为状态变量,x(0)为初值;φ(x)为非线性项函数;u(x)为控制器;ε(t)∈Rn为系统的随机干扰;ε(t)为单位维纳过程。

非线性随机系统的状态变量的概率密度函数[11]表示为

(2)

式中,D为归一化常数。

为了使非线性随机系统的概率密度函数pa(x)尽可能地接近期望的概率密度函数pd(x),设计优化目标函数为

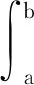
(3)

式中,a和b分别代表随机变量x的最小值和最大值。

当目标函数J取极小值时,可以实现实际的概率密度函数无限接近期望的概率密度函数。式(2)中含有控制器u(x),那么存在一个最优的u(x)可使得目标函数J最小。设计控制器u(x)为多项式,其表达形式为

u(x)=c0+c1x+c2x2+…+cnxn

(4)

式中,c0,c1,c2,…,cn分别为控制器增益,n为控制器的阶数。

2 粒子群算法

粒子群算法通过模拟鸟群捕食行为中的寻食过程,将待求解问题转化为一个多粒子系统的协同寻优过程。在迭代过程中,每个粒子沿着当前已知最优解和自己历史上的最优解进行移动,直到找到全局最优解或达到迭代次数的上限。

假定S维的目标搜索空间中,有N个微粒组成一个粒子群,则第j个微粒的空间位置表示为

Xj={Xj1,Xj2,…,XjS}

式中,Xmin≤Xj≤Xmax。

微粒的空间位置Xj就是求解优化问题式(3)中的一个解。根据空间位置向量可以计算出相应的适应度值,从而判断每个微粒的优劣。每个微粒的飞行速度记为

Vj={Vj1,Vj2,…,VjS}

式中,Vmin≤Vj≤Vmax。

在第j个微粒飞行过程中,计算出具有最好适应值的位置被称为个体历史最优位置,表示为

bj={bj1,bj2,…,bjS}

在整个微粒群飞行过程中,经历过的最好位置被称为全局历史最优位置,表示为

q={q1,q2,…,qS}

粒子群中第k代微粒的速度方程和位置方程分别表示为

Vj(k+1)=Vj(k)+C1R1[bj(k)-Xj(k)]+C2R2[q(k)-Xj(k)

(5)

Xj(k+1)=Xj(k)+Vj(k+1)

(6)

式中:R1～U(0,1)和R2～U(0,1)均为随机函数,相互独立;C1和C2分别为速度更新时的加速常量,通常取值为(0,2)。调节C1可以使微粒朝着自身最优位置方向前进,调节C2可以使微粒朝着全局最优位置前进。

3 蒙特卡罗方法

蒙特卡罗方法可以实现定积分的求解或者估算。当被积函数形式比较复杂时,采用传统积分方法往往难以求解或者计算精度明显降低,可以考虑蒙特卡罗方法求出复杂定积分的值。基于蒙特卡罗方法求解定积分,是使用随机抽样模拟函数在积分区间上的取值,从而估算出定积分的值[21-23]。蒙特卡罗法求解定积分的方法包括随机投点法和期望法,期望法求解原理如图1所示。

图1 期望法求解原理

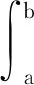
f(x)是随机变量x的函数,其数学期望的表达式为

(7)

如果x服从[a,b]区间内的均匀分布,即p(x)=1/(b-a)。取N个随机样本x1,x2,…,xN,可得到

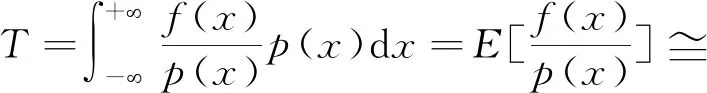
(8)

随着采样数n的增大,估计值会越接近准确值。然而大多数情况下,x并不服从[a,b]上的均匀分布,从而导致上述方法存在较大的误差。

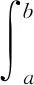
(9)

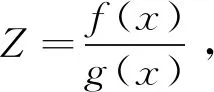
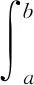
(10)

根据式(7)和式(10)可进一步推导得到

(11)

式(11)就是蒙特卡罗期望法计算定积分的一般形式。

4 PDF形状控制策略

基于粒子群-蒙特卡罗的PDF形状控制策略采用粒子群算法进行参数优化,并引入蒙特卡罗积分方法对目标函数J进行求解,从而获得最优的控制器。该策略的具体流程如图2所示。

①在立模上用墨线弹出标高线。以人工均匀摊铺，虚铺厚度一般为实际厚度的1.05～1.20倍。摊铺时应找准平整度与排水坡度，施工时对边角处特别注意有无缺料现象，要及时补料进行人工压实。

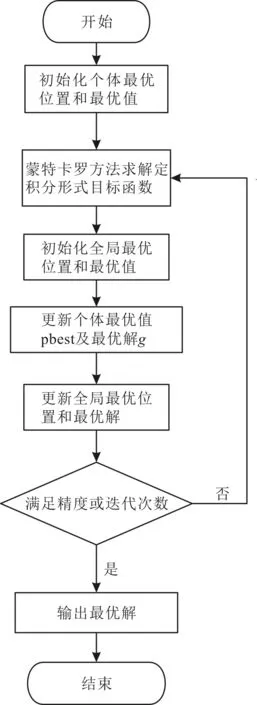
图2 PDF形状控制策略流程

基于粒子群-蒙特卡罗的PDF形状控制策略求解控制器增益的具体步骤如下。

步骤1设定粒子数N和最大迭代次数k,初始化每个粒子的初始位置Xj和速度Vj。将优化问题(3)的目标函数J作为适应度函数,初始化全局最优位置q,即参数最优值。

步骤2采用蒙特卡罗方法计算适应度函数J,即目标函数的值,根据当前粒子群中所有粒子Xj的适应度值,更新全局最优解q和局部最优bj。其中,全局最优是全部粒子历代适应度最好的粒子对应的位置,而每个粒子记忆的历代最佳位置则为其所在邻近范围内的最好位置。

步骤3根据式(5)和式(6)更新粒子位置Xj和速度Vj。根据当前粒子的位置、速度、全局最优和局部最优更新下一代粒子的运动状态。

步骤4判断Vj和Xj是否达到速度边界[Vmin,Vmax]和位置边界[Xmin,Xmax]:若Vj≤Vmin,则Vj=Vmin;若Vj≥Vmax,则Vj=Vmax;若Xj≤Xmin,则Xj=Xmin;若Xj≥Xmax,则Xj=Xmax。当达到最大迭代次数k,则输出当前全局的最优解q。

采用优化算法得到控制器增益的最优解后,将最优解q代入式(4)中的u(x),再将u(x)代入式(2),从而得到非线性随机系统状态变量最优的概率密度函数pa(x)。

5 仿真实验及结果分析

考虑某一维非线性随机系统的非线性项函数为

φ(x)=1-0.5x-x2

(12)

假设期望的概率密度函数pd(x)是标准的正态分布,即均值μ=0,方差σ=1,则其数学表达式为

(13)

u(x)=c0+c1x+c2x2

(14)

将式(12)、式(13)和式(14)代入目标函数式(3)中,得到关于控制器增益的函数的表达式为

J=

(15)

在Matlab环境下进行仿真实验。实验中设置粒子群的参数分别为:群体粒子个数j=2 000;粒子维数S=3;最大迭代次数k=30;加速常量C1=C1=1.5;速度边界Vmin=[-1,-1,-1],Vmax=[1,1,1];位置边界Xmin=[-100,-100,-100],Xmax=[100,100,100]。

通过粒子群-蒙特卡罗的PDF形状控制策略获得式(14)中控制器增益的最优值分别为c0=-7.072 7,c1=0.500 2,c2=0.499 6。在群体粒子个数和最大迭代次数相同的情况下,分别使用传统的数值积分方法和蒙特卡罗方法计算定积分形式的目标函数(适应度函数),其适应度进化分别如图3和图4所示。

图3 数值积分方法的适应度进化

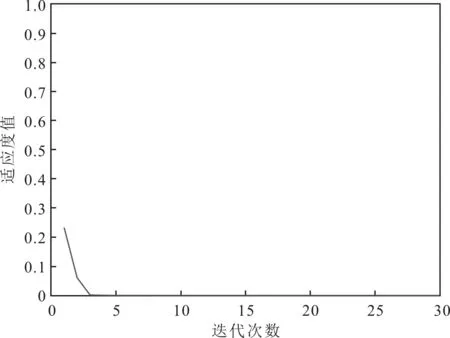
图4 蒙特卡罗方法的适应度进化

分别对比粒子群算法和引入蒙特卡罗方法后粒子群算法的计算时间,结果如表1所示。

表1 两种算法计算时间对比

同时观察图3、图4和表1可以发现,在不影响适应度函数曲线的情况下,粒子群-蒙特卡罗算法计算时间由56 s降低到3 s,计算速度明显变快。这是因为将蒙特卡罗方法引入粒子群算法求解定积分后,避免了传统数值积分方法存在的误差累积问题,从而提升了粒子群算法在非线性随机系统PDF形状控制器增益求解中的性能。

当算法结束时,目标函数J=7.256 5×10-9是一个极小的一个值,说明状态变量的PDF和期望的PDF近乎相同。基于粒子群-蒙特卡罗的PDF形状控制策略的PDF形状控制结果如图5所示,可以看出,状态变量的PDF可以很好地跟踪期望的PDF。因此,该控制策略达到了非线性随机系统PDF形状控制的目的。

图5 PDF形状控制结果

6 结语

针对非线性随机系统PDF形状控制问题,提出了一种基于粒子群-蒙特卡罗的PDF形状控制策略。设计了多项式形式控制器和误差平方积分性能指标,利用粒子群算法优化控制器增益的同时,采用蒙特卡罗方法计算目标函数,从而获得了PDF形状控制器增益的最优解。实验结果表明,该控制策略不但解决了PDF形状控制问题,而且计算时间明显减少,提升了粒子群算法在PDF形状控制器增益中的优化性能。