基于两级特征压缩BP神经网络的网络性能预测
2023-12-04赵紫汝畅志贤许艳红
赵紫汝,畅志贤,李 钊,许艳红
(1.西安电子科技大学 网络与信息安全学院,陕西 西安 710126; 2.西安邮电大学 通信与信息工程学院,陕西 西安 710121)
随着5G技术和应用的迅猛发展,无线网络规模急剧扩大,用户对网络性能的要求不断提高。方便、准确地分析和研究网络性能,不仅能够指导网络的建设和运维,也对网络资源的动态配置具有重要意义[1]。一方面,由于网络的性能指标直接反映了网络提供服务的能力,根据时延、丢包率、吞吐量等网络性能指标可以对网络服务质量(Quality of Service,QoS)以及网络存在的问题进行分析和预测,确定瓶颈节点或链路,指导网络资源的配置。另一方面,为了适应不同类型的业务,需要对网络性能进行准确分析和认识,进而合理分配网络资源,使网络性能能够满足不同业务的需求[2]。
网络态势感知方法通过研究整个网络的当前状态和变化趋势,为用户提供关于网络的宏观理解[3]。然而,网络态势感知只能预测某个时间点的网络整体状态,无法对具体的网络性能指标进行分析,其预测结果难以用于指导网络资源配置。基于模拟仿真的网络分析方法可以利用网络仿真软件如OPNET(Optimized Network Engineering Tool)、NS-3(Network Simulator-3)和OMNeT++(Objective Modular Network Testbed in C++)等获得网络性能并进行分析[4]。然而,该方法无法对历史仿真数据进行利用,使其在每次网络结构、协议或参数发生改变时,都需要在网络仿真软件上重新搭建网络模型或重新配置网络协议和参数,导致工作量增加和效率降低。
实际上,历史数据是宝贵的资源,若是能够对网络仿真历史数据进行收集,并利用机器学习方法从历史数据中获得网络运行的规律,便可以在不重复进行网络搭建、参数配置和仿真的条件下高效地预测网络性能。
目前应用于网络性能预测的机器学习模型主要包括统计模型和神经网络模型两种[5-6]。统计模型通常针对单一网络参数进行基于时间序列的预测[5],无法同时分析多个网络参数对网络性能的影响。与之相对应,神经网络模型则可以同时进行多个网络参量的数据拟合。特别是误差反传多层前馈(Back Propagation,BP)神经网络模型,由于其能够以任意精度逼近任何非线性函数[6],并且具有高度的自学习和自适应能力,得到了广泛的应用。
利用BP神经网络可以对不同网络参数下的网络性能指标进行预测,进而分析不同网络参数对网络性能的影响。然而,影响网络性能的网络参数的种类众多,这些网络参数中,有的参数与网络性能指标并非高度相关,或者不同的网络参数可能对同一网络性能指标具有相似的影响,即存在冗余,若不做处理地将这些参数作为BP神经网络预测模型的输入对其进行训练,不仅会增加模型的复杂度,导致训练收敛速度慢,还会使模型的泛化能力下降,出现过拟合情况[7]。为此,有必要通过特征选择[8-11]来降低输入BP神经网络的特征参数的数量。
特征选择的关键是目标函数的选取。目标函数通过评价特征子集的质量指导特征的筛选。根据目标函数的不同,特征选择方法主要包括过滤法和包裹法两种方法[7]。过滤法利用数据的内在联系,例如,输入特征与输出标签之间的互信息或相关度作为特征的评分依据[8-10],通过过滤掉评分低的特征以减少特征数量。过滤法计算复杂度较低,其对特征的选择独立于预测模型,有可能导致对于具体的预测模型,其选择结果不一定最优。包裹法以预测模型的性能作为目标函数,对所选特征进行评估[11],即在使用特征对预测模型进行训练时,根据模型的输出对所选特征进行评分,从而得到与预测模型适配的特征子集。但是,包裹法需要遍历所有可能的特征子集,将各个特征子集输入至模型中训练并计算预测误差,其计算复杂度较高,训练效率较低[8]。
为了更简便、准确地根据无线网络的多个特征预测其性能,本文拟提出一种基于两级特征压缩BP神经网络(Two-Stage Feature Compression based BP Neural Network,2SFC-BPNN)的网络性能预测方法,分析不同网络参数对网络性能的影响。首先,在网络仿真软件中搭建无线网络模型并进行仿真,对多次仿真的网络参数数据(特征)和网络性能指标数据(标签)进行收集,以建立数据集。其次,建立多输入、多输出的BP神经网络预测模型,一方面,利用网络参数之间的数学关系,通过初等函数运算得到衍生网络参数,然后,利用衍生网络参数替换原始网络参数,以此实现第一次特征压缩,称为特征简并;另一方面,根据网络参数数据与网络性能指标数据的相关度和网络参数数据之间的冗余度计算特征的优选权重,然后,基于该权重逐一搜索、添加特征并训练BP神经网络,同时,对训练得到的网络模型的预测质量进行评价,以确定优选特征子集以及该特征子集对应的预测模型,至此完成第二次特征压缩,称为特征优选。最后,利用两级特征压缩后得到的BP神经网络即可对无线网络性能进行预测,以改善经典BP神经网络模型泛化能力差的问题,并且降低特征冗余。
1 系统模型
图1给出了利用2SFC-BPNN进行网络性能预测模型的设计框架。如图所示,设计的2SFC-BPNN预测模型主要包括数据采集、预测模型建立以及模型评价等3个部分。首先,利用OMNeT++搭建无线网络并进行仿真,采集多次仿真中的网络参数(特征)和网络性能指标(标签),完成数据集构建。其次,简并、优选特征数据集并训练得到可用的BP神经网络模型。最后,以平均绝对百分比误差(Mean Absolute Percentage Error,MAPE)作为评价函数,利用特征优选后的测试集数据对输出的预测模型质量进行评价,当预测结果的MAPE大于预设的阈值时,调整预测模型的超参数,重新执行特征优选操作,并在优选过程中重新训练BP神经网络;反之,当预测结果的MAPE小于预设阈值时,则得到可以用于网络性能预测的预测模型。

图1 2SFC-BPNN网络性能预测模型设计框架
在利用OMNeT++搭建网络并进行仿真时,涉及r个原始网络参数和k个网络性能指标。如图1所示,原始网络参数包括信号调制阶数、网络节点间距、平均包长、节点个数、链路速率、节点发射功率、节点包的到达率、时隙长度以及子时隙数等9个参数,即r=9。其中,子时隙数由OMNeT++仿真过程中,数据包的传输时长和节点分配的时隙长度共同决定,即一个时隙被划分为多个子时隙用于数据包发送,一个子时隙用于传输一个数据包。网络性能指标包括分组平均时延和网络吞吐量两个指标,即k=2。设置N组不同的原始网络参数数据对搭建的网络模型进行N次仿真,可以得到N组网络性能指标数据,据此构建原始网络参数数据集和网络性能指标数据集,将其写作矩阵形式,分别记为M和K,K∈N×k,M∈N×r,表示实数空间。将M和K合并为网络数据集C∈N×(r+k),即C=[MK]。
在图1中,为了体现特征维数的压缩,将C、特征简并后的网络数据集C(Ⅰ)和特征优选后的网络数据集C(Ⅱ)以转置的形式进行表示。将C的N行(组)数据划分为训练(Training)数据集、验证(Validation)数据集和测试(Testing)数据集,划分的比例系数设置分别为αtr、αv和αte,αtr,αv,αte∈(0,1),满足αtr+αv+αte=1。训练数据集用于训练BP神经网络,验证数据集用于在特征优选阶段对特征子集的质量进行评价,测试数据集则用于评价BP神经网络的超参数设置。具体地,原始网络参数训练数据集Mtr∈αtrN×r,原始网络参数验证数据集Mv∈αvN×r,原始网络参数测试数据集Mte∈αteN×r。类似地,将网络性能指标训练数据集、网络性能指标验证数据集和网络性能指标测试数据集分别表示为Ktr∈αtrN×k,Kv∈αvN×k和Kte∈αteN×k。于是,C可以被重新表示为
特征简并后的网络数据集可以被表示为
特征优选后的网络数据集可以被表示为
在实际应用过程中,参数N、αtr、αv和αte的选择需要保证αtrN、αvN和αteN均为整数。
2 两级特征压缩方法设计
利用网络仿真软件OMNeT++搭建网络并进行仿真,可以获得多组的网络参数输入和网络性能指标输出数据,若将全部的网络参数作为BP神经网络的输入,会造成网络模型的规模过大和复杂度过高等问题。并且,由于仿真数据的采集会带来较高的成本,数据集的样本数量通常是有限的。过多的特征输入和过少的样本数据量会导致模型因学习大量的无关信息而产生泛化能力变差等问题。针对上述问题,本节将给出2SFC-BPNN的无线网络性能预测方法设计,通过对网络参数进行简并和优选,以在获得较好的预测性能的同时,降低BP神经网络的复杂度。
2.1 特征简并
在得到网络数据集C并对其进行划分后,接下来,对原始网络参数数据集M进行特征简并操作,得到简并后的网络参数数据集M(Ι)。具体采用如下操作。
根据M中的不同原始网络参数之间的数学关系,对原始网络参数进行初等函数运算以获得一个衍生参数。使用衍生参数替代产生该衍生参数的原始网络参数。令
式中,m1,m2,…,mN表示M中的原始网络参数向量,每个原始网络参数向量包含r个不同的原始网络参数。
对于任意mn∈M,其中n∈{1,2,…,N},若存在βn,则使用βn替换mn中的元素mnx,…,mny,即删除mn中的元素mnx,…,mny,并在mnx的位置添加βn,得到简并后的网络参数数据向量m′n。βn的数学表示式为
βn=f(mnx,…,mny)
式中:f(·)表示初等函数;mnx,…,mny为mn中的原始网络参数元素(这些网络参数元素可以不连续),其中x,y∈{1,2,…,r},且y>x。
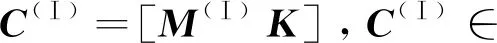
根据无线通信网络参数之间的物理联系,可以对原始网络参数进行特征简并。以无人机集群网络项目搭建的OMNeT++仿真网络的常用参数为例,原始网络参数包括信号调制阶数、网络节点间距、平均包长、节点个数、链路速率、节点发射功率、节点包的到达率、时隙长度以及子时隙数等9个参数。在信号带宽一定的情况下,调制阶数越高,则信息传输速率越大,说明调制阶数会影响链路速率。并且,节点间距离决定链路长度,而链路长度与节点发射功率又共同影响节点的接收功率,进而影响链路速率。因此,根据特征简并的设计思想,由调制阶数、节点间距和节点发射功率可以衍生出链路速率,更进一步,可以使用链路速率替代调制阶数、节点间距和节点发射功率等3个参数,最终得到包含平均包长、链路速率、节点包到达率、时隙长度、子时隙数以及节点个数的简并后的网络参数。
2.2 特征优选
为了进一步减少输入BP神经网络的特征数,即网络参数的数量,使用标签与特征的相关系数表征相关度,应用特征和特征之间的相关系数表示冗余度,并基于相关度和冗余度计算特征优选权重,进行网络参数的优选。
首先,选择一个与标签相关度最大的特征作为初始特征加入优选特征子集。由于预测模型有多个标签输出,因此,需要分别计算特征与所有标签的相关系数之和,选择相关系数之和最大的特征,以确保所选特征对标签数据具有较强的表达能力。接下来,在候选特征集合(包含未添加至优选特征子集的特征)中搜索合适的特征并添加至优选特征子集中。为了防止由于所选特征之间冗余度过高而出现的多重共线性问题,同时保证特征与标签具有较高的相关度,根据候选特征与已选特征之间的冗余度、候选特征连同已选特征与标签之间的相关度,计算每个候选特征的优选权重,并将优选权重最小的特征添加至优选特征子集中。
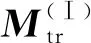
为了便于叙述,将简并后的M(Ⅰ)包含的r′个网络参数组成的集合称为特征集合D={d1,d2,…,dr′},满足r′=|D|,其中|·|表示集合包含的元素个数。类似地,将K包含的k个网络性能指标组成的集合称为标签集合U={u1,u2,…,uk},有k=|U|。特征优选的具体步骤如下。
步骤1初始化特征添加次数。令λ=1,初始化优选特征子集,令B=Θ,Θ表示空集。将D中未添加至B的特征组成的集合称为候选特征集合,记为D′,有D′=D-B,初始化候选特征集合,令D′=D,进行第一次特征优选,即从D中选择与U中所有标签的相关系数之和最大的特征。具体地,计算D′中的第i个特征与U中的第j个标签的Pearson相关系数[12]。Pearson相关系数的定义式为
(1)
式中:xi为第i个网络参数di∈D′(i∈{1,2,…,r′})对应的M(Ⅰ)中的数据向量;yj为第j个网络性能指标uj∈U(j∈{1,2,…,k})对应的K中的数据向量;cov(xi,yj)表示xi和yj的协方差;σxi和σyj分别表示xi和yj的方差。
由于预测模型为多输出BP神经网络,D′中的第i个特征与U中所有标签的相关系数之和的计算表示式为
(2)
选择D′中最大的si(i∈{1,2,…,r′})对应的特征,记为dg,将dg加入B,即B←B+{dg},并将dg从D′中删除,即D′←D′-{dg}。
步骤2更新λ。若λ=r′,说明D′中的所有特征都已经添加完毕,特征优选结束,将D′作为B;否则,当λ (3) 式中:ρxpxq表示B中的特征dp与D′中的特征dq的Pearson相关系数,dp∈B,p∈{1,2,…,r′},dq∈D′,q∈{1,2,…,r′},且p≠q;sp和sq分别为dp和dq与U中所有标签的相关系数之和。 将式(3)中的ρxpxq/(sp+sq)称为优选系数,其表示候选特征dq与已选特征dp之间的冗余度与相关度的比值,该数值越小,说明dq与dp的相关度越高且冗余度越低。由于B中包含多个已选特征,因此,hq为D′中的第q个特征与B的所有已选特征的优选系数之和。在D′中选择优选权重最小的特征dv添加至B,即B←B+{dv},并更新D′←D′-{dv}。 (4) 同样地,根据式(4),可以得到第λ次特征添加后训练好的神经网络netλ以及由式(4)得到的该网络预测结果的MAPE,记为γλ。 为了便于理解,下面给出了特征优选算法的伪代码。 算法:特征优选算法输入:M(Ⅰ)tr,M(Ⅰ)v,Ktr,Kv,标签集合U,特征集合D,简并后的网络参数个数r'输出:优选特征子集B,训练好的网络n^et1: 初始化:λ=1,B=Θ,候选特征集合D'=D2: 根据式(1)计算D'中的第i个特征与U中第j个标签的相关系数ρxiyj;根据式(2)计算D'中第i个特征与U中所有标签之间的相关系数之和si3: while λ 为了验证所提方法的有效性,使用MATLAB提供的神经网络工具箱搭建BP神经网络模型,并对其进行训练和测试。使用的计算机设备处理器为Intel Core i5-1240,内存为16 GB。 利用OMNeT++搭建无线网络、进行仿真并采集数据。在预测网络性能指标时,训练模型所用的数据集涉及多种网络参数和网络性能指标,而实际的网络形式多样,适用于各种网络,能根据不同网络参数预测任意网络性能指标的公开数据集难以获得,已有的一些相关研究通常利用网络仿真建立符合要求的数据集[13-14]。因此,仿真利用OMNeT++建立实现、验证2SFC-BPNN所需的数据集。 由于无线网络在不同的网络参数设置下存在传输能力的上限,单位时间内网络中任意节点的包到达数与其单位时间内能够传输的包数的比值称为业务强度因子。当业务强度因子小于1时,网络未达到其传输能力上限;当至少存在一个节点的业务强度因子大于1时,网络达到其传输能力上限。当网络的业务负荷达到其能力上限后,网络性能将趋于饱和甚至恶化;当业务负荷未达到网络能力上限时,网络性能指标则会随机波动。因此,不同的网络业务负荷会使网络性能指标表现出明显的差距,进而影响BP神经网络的预测性能。 基于上述考虑,分别在网络是达到和未达到其能力上限两种情况下构建数据集,并进行网络性能预测。除此之外,由于特征简并利用网络参数之间的数学关系对网络参数数量进行压缩,而网络参数之间的数学关系复杂,造成了第一级特征简并操作的特征压缩得到的参数组合不唯一,因此,选择不同的参数组合进行差异化实验。 表1给出了在不同业务负荷下构建的网络数据集Data1、Data2和Data3。可以看出,不同数据集包含不同的网络特征参数,预测的网络性能指标(标签)均包括网络吞吐量和分组平均时延。每个数据集包含N=103组原始网络参数数据和网络性能指标数据,对应于103次网络仿真。将上述原始网络参数数据集和网络性能指标数据集组成的网络数据集按照比例αtr∶αv∶αte=8∶1∶1划分为训练数据集、验证数据集和测试数据集。 表1 网络数据集 接下来,使用MATLAB提供的神经网络工具箱搭建BP神经网络模型,并利用上述数据集Data1、Data2和Data3对其进行训练和测试,训练采用的算法为贝叶斯正则化算法。当训练得到的模型预测误差MAPE小于预设的阈值20%时,则获得可用的预测模型。表2给出了BP神经网络的参数设置。仿真结果表明,利用表2中的参数建立的BP神经网络的预测MAPE均小于20%。 表2 BP神经网络的参数设置 OMNeT++网络仿真模型根据某基于Link16数据链的无人机集群网络项目搭建,网络节点采用时分多址(Time Division Multiple Access,TDMA)接入方式,网络参数包括调制阶数、节点间距、节点发射功率、平均包长、链路传输速率、分组到达率、时隙长度、节点个数以及子时隙数等9种网络参数。表3给出上述9种网络参数的取值情况。 表3 网络参数及其取值范围 图2 网络吞吐量的预测性能 图3 分组平均时延的预测性能 接下来,对两级特征压缩中的特征优选进行复杂度分析。分别使用数据集Data1、Data2和Data3进行103次神经网络训练,每次训练的网络初始权值均由随机方式产生。根据实验设置,Data1、Data2和Data3等3个网络数据集均包含4个特征,由于此时的特征维数较低,特征优选有可能选择全部4个特征构成优选特征子集。 为了验证特征优选对模型结构复杂度,即模型的输入特征数量的降低,在使用2SFC-BPNN方法对吞吐量或时延进行预测时,分别在Data1、Data2和Data3等3个数据集中对特征优选得到的特征子集包含的不同数量特征的概率进行统计。预测模型为多输入——二输出的BP神经网络,输入的维数取决于优选特征子集的元素数。进行103次实验,当特征子集的元素数分别为1、2、3、4时,特征优选得到的特征子集包含不同数量特征的概率分布情况实验结果如图4所示。 图4 特征子集包含不同数量特征的概率 如图4所示,在103次实验中,对网络数据集Data1有7%、38%、29%和26%的概率选择1个、2个、3个和4个特征;对Data2分别以5.8%、4.4%、63.4%和26.4%的概率选择1个、2个、3个和4个特征;对Data3有7.2%、3.6%、57.8%和31.4%的概率优选1个、2个、3个和4个特征。根据图4可以计算得到数据集Data1、Data2和Data3的概率加权平均优选特征个数分别为2.780、3.104和3.134,即平均优选特征数量均相比于特征优选前的4个特征减小约24.9%,证明了特征优选算法能够对特征进行优化选择,即能够筛选掉对预测性能没有贡献的特征。说明通过特征优选,可以降低BP神经网络的结构复杂度。 此外,进行103次实验,分别统计2FSC-BPNN与不进行特征优选的BP神经网络的平均训练时间。实验结果如表4所示,可以看出,对于数据集Data1、Data2和Data3,相比于不进行特征优选的模型平均训练时间,所提方法可以将模型训练时间分别缩短8.48%、1.43%和13.46%,平均改善量约为7.79%,说明所提2FSC-BPNN方法能够降低BP神经网络训练的时间复杂度。 表4 模型平均训练时间 最后,对所提方法对预测精度的改善进行验证。将所提方法与利用最大相关度最小冗余度准(minimal-Redundancy-Maximal-Relevance Criterion,mRMR)方法[9]、ReliefF算法[10]、前向搜索(Sequential Forward Selection,SFS)方法[10]选择特征并进行BP神经网络训练,进而用训练好的模型进行时延和吞吐量预测的平均MAPE进行对比。 mRMR方法和ReliefF方法均属于过滤方法。mRMR方法利用特征与特征、特征与标签的互信息对特征进行评分,从而选择与标签相关度最大、与其它特征冗余度最小的特征子集;ReliefF方法利用特征与标签样本的数值邻近程度赋予特征不同的权重,权重越大表明特征的贡献程度越高。SFS算法属于特征选择适配于模型的包裹方法,该方法根据模型的预测性能逐一搜索添加特征,直至得到优选的特征集合。利用Data1、Data2和Data3等3个数据集分别进行103次实验,并相应地统计所提2SFC-BPNN方法对吞吐量和时延预测的平均MAPE,即对103次实验得到的103个MAPE样本取平均。需要指出的是,mRMR方法、ReliefF方法以及SFS算法需要预先指定降维后的特征数。为了形成对照实验,在每次实验中将特征优选算法中选择的特征个数作为其它特征选择方法的预设特征数。使用不同特征选择方法对Data1、Data2和Data3等3个数据集网络吞吐量和分组平均时延的预测平均MAPE实验结果如表5所示。其中,使用全部特征记为方法All。表5中加粗的数值表示使用不同特征选择方法对特定网络性能指标进行预测时的平均MAPE的最小值。 表5 不同特征选择方法的预测平均MAPE 表5显示,对于网络吞吐量,基于所提特征优选算法得到的模型在数据集Data1、Data2下的预测精度最高,在Data3下的表现略差于其它方法。对于分组平均时延,所提方法的平均MAPE最小。并且,所提2FSC-BPNN方法在Data1、Data2和Data3这3个数据集下的预测精度均优于不进行特征选择的方法。具体地,对于数据集Data1、Data2和Data3,相对于不进行特征优选,2FSC-BPNN方法对网络吞吐量的预测精度分别提高了24.0%、12.4%和9.8%,即平均预测精度提高了约15.4%;对于分组平均时延的预测,2FSC-BPNN方法的预测精度分别提高了9.8%、3.7%和4.4%,即平均提高了约6.0%。这是因为,在训练神经网络模型时,并非所有特征都适合于对网络性能指标的预测,筛选掉这些冗余特征可以避免模型学习到无关的信息,从而提升模型的泛化能力,改善其预测性能。该实验证明了所提特征优选方法能够有效提高网络性能指标的预测精度。 提出了一种基于两级特征压缩的BP神经网络无线网络性能预测的2SFC-BPNN方法。该方法首先对使用OMNeT++搭建的无线网络进行仿真,以建立网络参数数据集和网络性能指标数据集,然后,使用数据集对BP神经网络进行训练以获得预测网络模型,并且在训练过程中对输入神经网络的网络参数进行两级特征压缩。特征压缩过程包括特征简并和特征优选。在获得训练好的BP神经网络后,对网络性能指标进行预测。2SFC-BPNN方法的特征简并操作能够有效减少特征数量,特征优选操作能够兼顾特征与机器学习模型的适配和特征选择复杂度的降低。实验结果表明,所提2SFC-BPNN方法能够在降低预测模型复杂度的同时,获得较好的预测性能。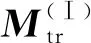
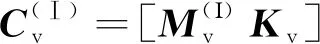

3 仿真及分析




4 结语
