基于逆距离徙动校正的前视SAR 成像算法

刘金升，张朝晖，韩 松

（1.中国科学院空天信息创新研究院，北京 100190；2.中国科学院大学 电子电气与通信工程学院，北京 100049）

0 引言

合成孔径雷达(Synthetic Aperture Radar，SAR)是一种高分辨率成像雷达。在资源调查、海洋监视、灾害监测等遥感领域获得了广泛应用[1]。前视SAR 成像雷达可以对平台前下方进行成像，在飞机辅助着陆、地面搜寻有着广泛应用，随着近年来自动驾驶的发展，前视成像雷达在汽车领域也有着广泛的应用场景和商业价值。

当雷达处于前视状态时，平台的运动与天线主波束指向基本一致，由平台运动产生的多普勒频率变化近乎消失，无法利用SAR 成像方法进行成像[2]。德国宇航局（DLR）最先提出了视景增强区域成像雷达(Sector Imag‐ing Radar for Enhanced Vision，SIREV)的前视SAR 成像方法[3-4]，其工作原理是通过在平台飞行方向的垂直方向线性排列一组天线阵元，通过切换接收回波的天线阵元，等效为传统侧视SAR 中“走停”模式。SIREV 系统中有“收发同置”和“收发分置”两种工作模式[5]，“收发分置”工作模式的设计成本相对较低，随着多输入多输出（Multiple Input Multiple Output，MIMO）雷达的发展，尤其基于线性调频连续波（Frequency Modulated Con‐tinuous Wave，FMCW）的MIMO 雷达技术越来越成熟，可以利用MIMO 雷达等效出线性分布的“收发同置”的天线阵列[6-7]。本文以FMCW 的前视阵列雷达作为研究对象。

相较于传统的侧（斜）视SAR 成像，前视SAR 成像的合成孔径由延切航迹分布的实孔径天线阵张成，由于实孔径长度受限，因此其只能利用方位向部分孔径，这点和扫描SAR(ScanSAR)中的单一Bust 成像类似，所以可以借鉴ScanSAR 的相关算法[8]。由于方位天线为实天线，近些年来不少学者从阵列天线的角度，采用超分辨算法作为前视成像方案[9-11]，该类算法可以实现前视雷达方位向的超分辨，但该类算法通常需要多次迭代，运算量较大，不适用于实时成像。

在前视SAR 成像过程中，由于其方位向调频率随距离空变，方位压缩后会造成图像的扇形畸变[12]。此外，随着天线波束角的增加，波束照射范围内的大部分目标无法被景中心穿过，采用对方位向补零的方式将天线孔径扩展到全孔径又会增加处理的数据量。

针对采用SAR 成像算法方位压缩后图像扇形畸变的问题，提出了基于方位频域逆距离徙动校正（IRCMC）的前视成像方法。对距离压缩后的回波信号，通过傅里叶变换到距离多普勒域进行距离徙动校正，通过SPECAN 的方法，将信号转换到时域进行去斜压缩后再变换到距离多普勒域，然后通过逆距离徙动校正，将目标校正回瞬时斜距的位置，最后通过坐标映射完成成像。

本文首先介绍了前视SAR 的工作原理，给出了FMCW 体制下的回波方程，分析了前视SAR 的回波特性。给出该文提出的成像方法和算法流程图，最后通过仿真实验验证了方法的可行性。

1 前视SAR 工作原理及回波方程

前视SAR 的成像几何模型如图1 所示，平台沿x轴飞行，飞行高度为h，天线阵元在y轴方向线性分布。与传统SAR 成像不同，这里定义平台飞行方向为距离向，天线阵元张成的方向为方位向。天线阵元间隔为n倍波长，即d=n·λ，脉冲发射重复频率为PRF，则天线的切换速度vs=d·PRF。经过简单推导即可证明，在不考虑平台向前运动和低PRF 造成的运动误差的情况下，PRF对成像系统没有影响，为了简化处理和后续公式推导，这里取PRF=1，此时天线切换速度vs=d。

图1 前视SAR 几何模型

由于前视SAR 的天线为实天线，天线阵元的位置已经确定，设某一时刻工作的阵元位置为yi，且天线的空间位置和方位时间η有以下对应关系：

设目标P(x0,y0)到天线的最近斜距为R0，目标和天线中心的夹角为θt，目标到天线中心的距离为Rt，目标到天线的瞬时斜距为R(yi;y0,R0)。

设发射阵元发射的线性调频信号为：

式中：τ为距离向的快时间；Tr为脉冲时宽；fc为载频，Kr为LFM 信号的调频斜率。在不考虑天线方向图的情况下，雷达回波数据为：

式（5）中，σ为目标的后向散射稀疏；c 为光速。

在FMCW 雷达中，回波信号一般由硬件单元进行混频，输出信号为去斜后的中频信号，输出的中频信号为：

式（6）中第一个相位因子表示方位向相位历程，第二项为目标距离向信息，第三个相位为残余视频相位(RVP)，可以通过相位补偿的方式进行处理。令fτ=Krτ，经过IFFT 即可求解目标的距离信息，完成距离压缩。对式（6）进行傅里叶逆变换并补偿RVP 相得到距离压缩后的信号：

2 回波特性分析

2.1 方位回波特性

在正侧视SAR 成像算法中，瞬时斜距一般采用式（3）的形式，通过泰勒展开将双曲线近似为抛物线。但前视SAR 的合成孔径较短，波束角较大，这种近似误差较大。

由于前视SAR 的方位向由实天线阵张成，因此可以从阵列雷达的角度对回波进行分析。采用Rt和θt表示瞬时斜距，并在y=0 处展开:

将式（8）带入式（7），由于最后一项和目标的方位角耦合在一起，不容易求解，所以忽略该二次相位项，目标的方位信号为：

将式（1）中的时域和空域的对应关系式带入式（9）得到回波信号的方位向相位历程为：

第一项为包含距离信息的常数项，第二项包含目标方位角度信息，第三项包含目标方位向多普勒展宽的信息。对式（10）中的变量η求导，可求得方位多普勒频率：

由式(11)可知，在相同距离处的目标具有相同的多普勒带宽，但不同方位角上的目标的多普勒历程不同。因此可以对同一距离向的目标进行“去斜”处理，从而方位向频谱只剩下和目标方位角度相关联的相位项。

2.2 目标的距离徙动分析

由式（8）可知，目标的瞬时斜距R(yi)随方位时间变化，照射时间内目标的轨迹可能会经过不同的距离单元。此外，不同方位的目标距离徙动量不同，距离徙动量随着目标方位角度的增大而增大，目标点处的最大距离徙动量为：

其中La为天线长度。这和景中心斜距为Rt，斜视角为θr,c=θt的斜视SAR 的距离徙动表达式相同，不同的是这里的θt为地面目标的方位角度。这相当于多个不同斜视角的SAR 回波线性叠加的结果，无法通过斜视SAR的距离徙动校正方法对每个目标的徙动量进行校正。

根据式（3），可以从正侧视SAR 成像的角度进行距离徙动校正，将同一距离门的目标信号校正到R0的位置。后续会在算法实现中给出具体的距离徙动校正量。

图2 为经过方位FFT 后，多个目标的距离多普勒域图像。从图中可以更直观地体现式（11）目标方位频谱的特点。同时还可以观察到不同位置点目标的距离徙动。图3 为距离徙动校正后的图像，目标处的信号被校正到同一距离门，同时同一距离向的信号也被校正到同一距离门。

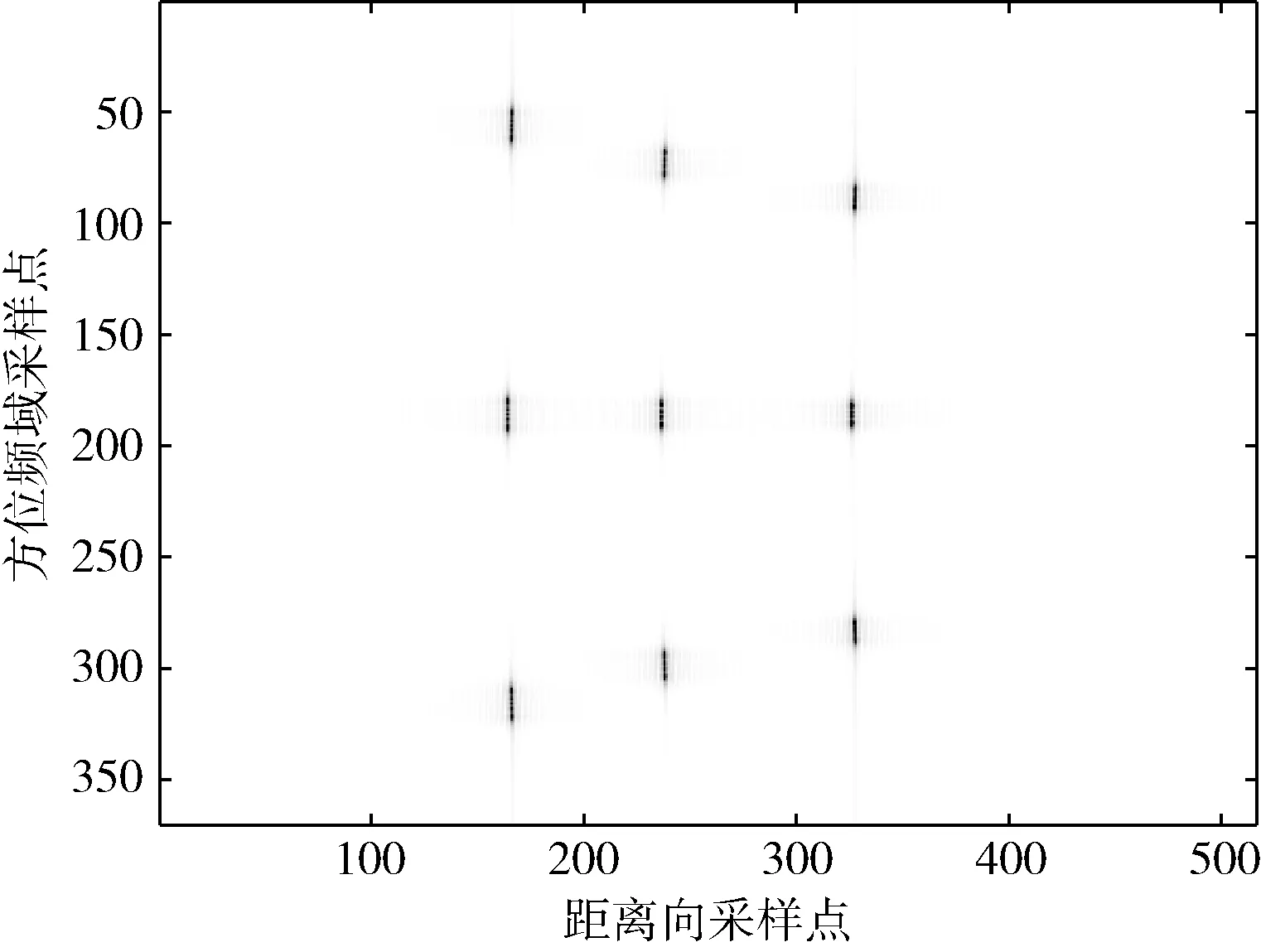
图2 距离多普勒域数据

图3 距离徙动校正后的数据

3 基于逆距离徙动校正的前视阵列SAR 成像算法

通过对目标回波特征的分析，本文提出基于逆距离徙动校正的前视阵列SAR 成像算法。FMCW 回波信号经过硬件去斜得到包含目标距离相位的中频信号，经过距离IFFT 完成距离向压缩。然后通过方位向FFT 在距离多普勒域进行距离徙动矫正，通过去斜的方式在R0处对目标进行方位压缩。采用IRCMC 的方法，将目标从R0位置处校正到Rt处，最后通过坐标系变换和地面投影变换完成成像。图4 为该算法的具体流程图。

图4 成像算法流程图

3.1 距离徙动校正

前视SAR 成像可以看作部分孔径的正侧视SAR 成像，所以可以利用侧视SAR 的模型分析前视SAR 的回波特性。在侧视SAR 中，目标到阵元的距离为：

距离多普勒域中的距离徙动量为：

在FMCW 雷达成像过程中，由于距离信号已被硬件解调，失去了Chirp 信号的特性，无法适用Chirp Scaling的方法进行距离徙动校正，可以采用插值的方法进行距离徙动校正，文献[13]给出了一种基于频率Scaling 的距离徙动校正方法，可以完成FMCW 回波信号的距离徙动校正。

假设目标通过距离徙动矫正到正确的位置，此时目标到天线中心的距离Rt变为R0，目标距离时域的表达式变为：

3.2 方位向压缩

通过对式(16)进行相位补偿，完成目标的方位向去斜，其表现形式和SPECAN 算法中的去斜操作一致。由于此时目标已经通过距离徙动校正从距离Rt处校正到参考距离R0处，相位补偿因子为：

经过相位补偿，目标的回波信号的横坐标是关于空间方位角的函数。忽略由于距离徙动校正后方位向调频失配造成的二次相位误差，补偿后的目标信号为：

对式（18）做方位向FFT 即可求解目标处的方位角度，目标照射时间Ta=La/vs。

3.3 逆距离徙动校正

由于目标是被校正到R0进行的方位向压缩，因此压缩后的目标仍然处于R0位置，而方位压缩后的方位向坐标系为2dsinθ/λ，在SPECAN 算法中，方位压缩后的信号出现扇形畸变是由于将该坐标看作方位向进行处理所引起的。SPECAN 的解决办法是对方位向根据采样间隔进行插值，或者通过变标傅里叶变换实现方位向的重采样。而本文方法则是通过逆距离徙动将目标位置校正回Rt位置，然后通过坐标转换的方式完成成像。

方位向压缩后的目标仍处在距离多普勒域，所以可以直接进行逆距离徙动校正，校正量为：

经过逆距离徙动校正后的信号为：

3.4 地面坐标系转换

经过逆距离徙动校正，目标信号从(R0,2sinθt/λ)位置校正到(Rt,2sinθt/λ)位置，通过式（22）坐标变换得到目标在地面二维平面的图像：

此步骤同时完成了坐标系映射和斜地变换。至此，已通过逆距离徙动的前视SAR 成像算法完成成像。

3.5 算法复杂度分析

本文算法的主要贡献是从逆距离徙动校正的角度，解决了频域算法中方位向调频率不一致产生扇形畸变的问题。实际上存在一种时域后向投影算法(Back Pro‐jection，BP)可以从根源上解决该问题。该算法目前在车载毫米波成像领域有所应用[14-15]。但BP 成像算法的时间复杂度为O(N3)。本文算法作为频域算法，其时间复杂度为O(N2log (N))，在实际应用中，成像速度要优于BP 成像算法。

相较于传统前视SAR 成像算法，本文算法通过逆距离徙动校正实现了扇形畸变的校正，避免了方位插值，但该算法需要两次距离徙动校正，且坐标转换和斜地变换同样需要插值。不过在SAR 成像系统中，坐标映射和斜地变换通常由后处理系统负责，在这种情况下，该算法和传统SAR 成像算法成像效率上主要体现在距离徙动校正和方位插值上。

在传统SAR 成像算法RDA 中，其方位压缩采用脉冲压缩的方式，需要两次FFT、一次复乘和一次IFFT。在扇形畸变校正时，需要方位插值。本文算法在方位向采用去斜压缩代替脉冲压缩，方位压缩时只需要一次复乘和一次FFT。针对扇形畸变的问题，即使采用sinc 插值的方法，其运算量和扇形畸变校正中的方位插值相当。

总体而言，本文算法在运算量上具有一定优势，实际应用中，还可以根据硬件和系统设计进行进一步优化。

4 实验仿真

为了验证本文算法的有效性，进行了9 点目标成像仿真，中心点目标坐标为（167 m，0 m）,距离向点目标间隔60 m，方位向点目标间隔20 m，点目标的具体分布如图5（a）所示。仿真参数如表1 所示，根据仿真参数，生成回波数据并采用本文方法进行成像处理。

表1 仿真参数

图5 成像结果

图5 展示了未经过逆距离徙动矫正和经过逆距离徙动矫正的成像结果。对实验结果进行分析，经过去斜处理后的信号，以纵坐标为方位向的角度去分析，在方位向存在扇形畸变（图5（b））。图5（c）为对方位压缩后的图像直接进行坐标变换的结果，可以观察到其在同一距离向的目标，位置存在一定的偏差。采用本文方法的结果如图5（d）所示，目标能量被聚焦到正确位置。

表2 提取了图中三个目标成像结果的位置误差，在近距离处，未经过IRCMC 的成像结果在距离向和方位向均存在较大误差，而采用本文方法，最终成像结果误差较小，基本控制在一个距离分辨率网格大小内。

表2 成像结果位置误差

为了验证本文方法的性能，提取了图中三个目标成像结果的距离向和方位向的峰值旁瓣比（PSLR）、积分旁瓣比(ISLR)和分辨率(IRW)。点目标的相应指标（未加窗）如表3 所示，PSLR 和ISLR 符合理论值。中心点目标的实际距离分辨率和方位分辨率与理论值相符。但成像中心两侧的目标实际方位分辨率与理论值存在误差，这是由于方位压缩时补偿相位舍弃了高阶相位所导致的。理论上，方位向上的目标，其观测角度越大，该误差越大。

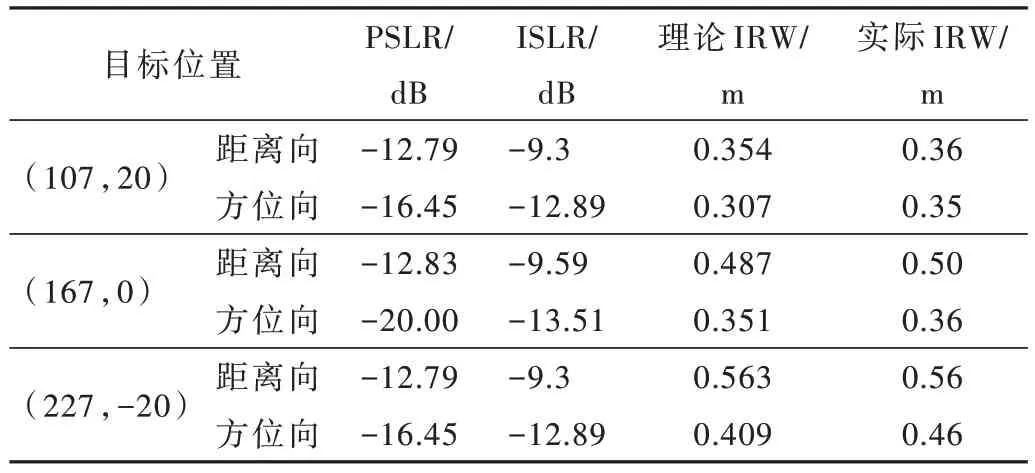
表3 点目标响应质量指标

本文通过MSTAR 雷达数据集进行成像实验，进一步验证本文方法的可行性。图6（a）为真实成像场景，图6（b）展示了经过方位去斜压缩后图像产生的扇形畸变，原本直行的道路出现弯曲。采用本文方法成像结果如图6（c）所示，道路畸变部分被校正到正确位置。

图6 MSTAR 反演数据成像结果

5 结论

本文分析了前视阵列SAR 的回波特性，根据其回波方位特性和距离徙动特性，提出了一种基于逆距离徙动校正的前视SAR 成像方法，解决了前视SAR 成像中扇形畸变的问题。研究的核心是从回波的信号的方位频谱进行分析，通过相位补偿的方法在回波信号的方位频域提取目标的方位角信息，通过逆距离徙动校正还原目标的距离信息。利用该方法进行仿真验证，证实了该方法的可行性。