基于卷积神经网络的海杂波数据分析与鉴别*

薛 冰，吴 巍

（海军工程大学，湖北 武汉 430033）

0 引言

由于海洋环境复杂多样，对海面目标的探测与识别影响显著。海杂波的成因复杂，海杂波具有不完全随机性，而且目标回波信号受多种因素影响，仅从单一方面研究其特性会有很大的偶然性与不精确性。此外，海杂波影响因素多样，所有构建的模型只能在某一段范围内符合海杂波的特性，其在较长的时间或距离单元跨度内，并不完全符合海杂波的特性。更重要的是，海杂波与目标的区分度不具一般性，规律不明显。本文通过提取海杂波与海面目标在某些方面的显著差异，再去利用卷积神经网络对其进行鉴别研究。

1 IPIX 雷达实测数据提取与统计特性分析

1.1 IPIX 雷达实测雷达数据集简介

IPIX 实测数据集是HAYKIN S 教授在1993 年利用布设在加拿大Dartmouth 海岸某海湾的固定位置上的IPIX 雷达对某一方向的固定海域照射，获得大量目标和海杂波的实测数据，从而建立了海量数据的IPIX 实测数据集[1]。本文进行的研究所使用/选择的数据是1993 年HAYKIN S 教授测得的在雷达凝视状态下的10 组数据（如表1 所示）。

表1 IPIX 实测数据算法运行时间比较

1.2 实测海杂波统计特性分析

海杂波是雷达照射到海面的回波信号。海杂波的幅度特性是海杂波的一项基本特性，基于大量理论研究和海杂波数据分析的基础之上，对特定应用背景下的杂波特性进行研究[2-4]，实现对目标与海杂波的区分与鉴别。

1.2.1 幅度均值

海杂波的幅度均值是指其幅度的算术均值，是海杂波的重要特征之一。对IPIX 实测数据而言，对其每一个距离单元中的数据幅度X={X1,X2,…，Xn}进行排序，定义每个距离单元中最大值为Xn，定义最小值为X1，其中极差det=Xn-X1。则幅度均值为：

其中x是第k个区间的均值。以第一组实验数据为例，其不同距离单元下的幅度均值如图1 所示。由图1 可以看出，主目标距离单元的幅度均值要比其他距离单元大很多，从而表征海杂波与海面目标在幅度这一统计特性上有明显的区分度。

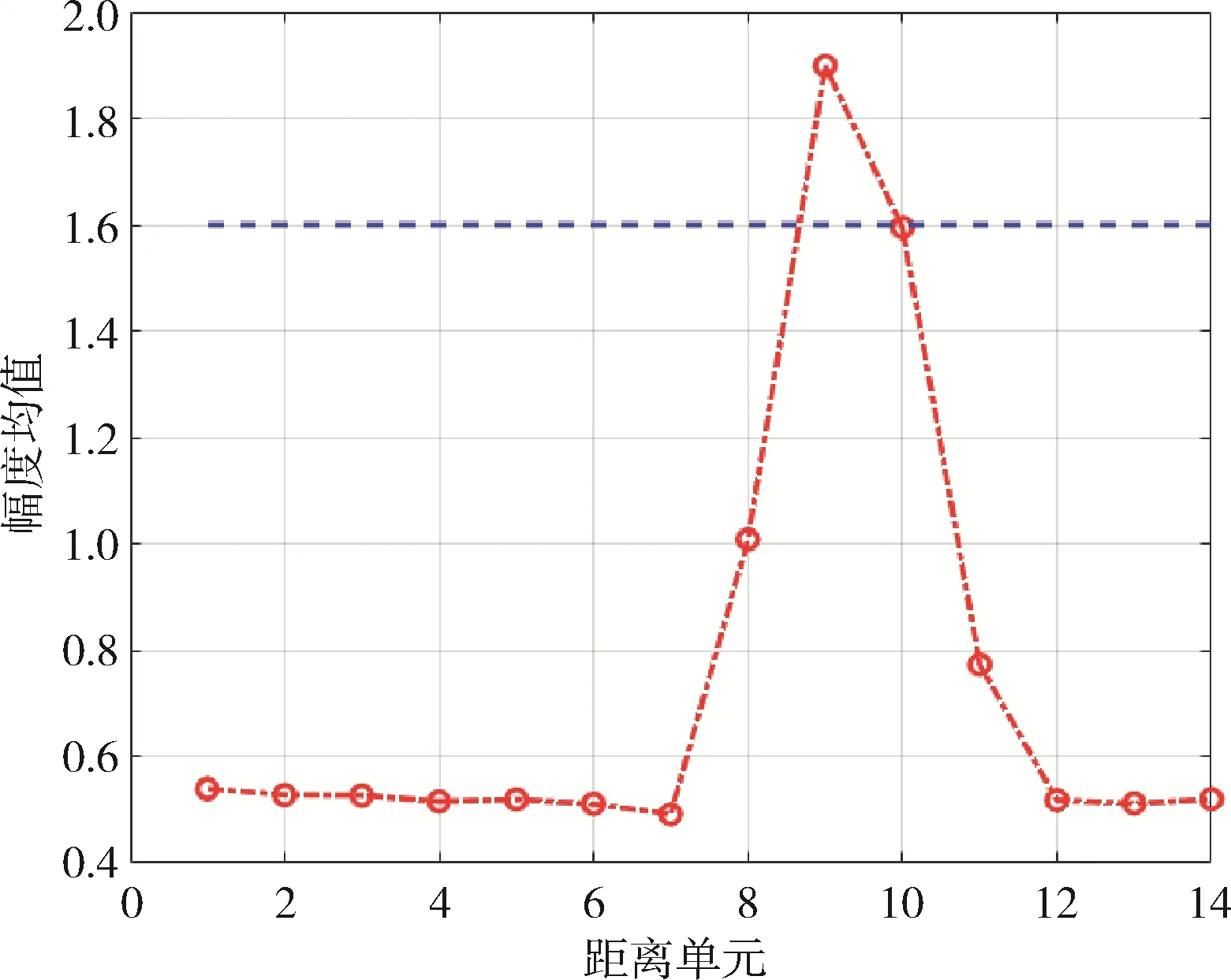
图1 幅度均值分布图

1.2.2 幅度方差

幅度方差是衡量随机变量离散程度大小的随机变量。对于IPIX 雷达实测数据而言，其幅度方差为：

其中，S2是幅度方差，det 是每个小区间的极差，λ是小区间的个数，x是每个小区间的均值。

以第一组实验数据为例，其不同距离单元下的幅度方差如图2 所示。从图2 可以看出，纯海杂波距离单元的幅度方差波动趋势较小，而主目标距离单元的幅度方差波动较大，纯海杂波距离单元的方差比目标距离单元小得多，而且接近于0。由图3 可以看出，高海况条件下由于“海尖峰”的存在，纯海杂波距离单元的波动趋势可能比目标单元更剧烈。只有在海情状况满足一定条件时，通过幅度方差这个特性才能较为显著地鉴别海杂波与海面目标。

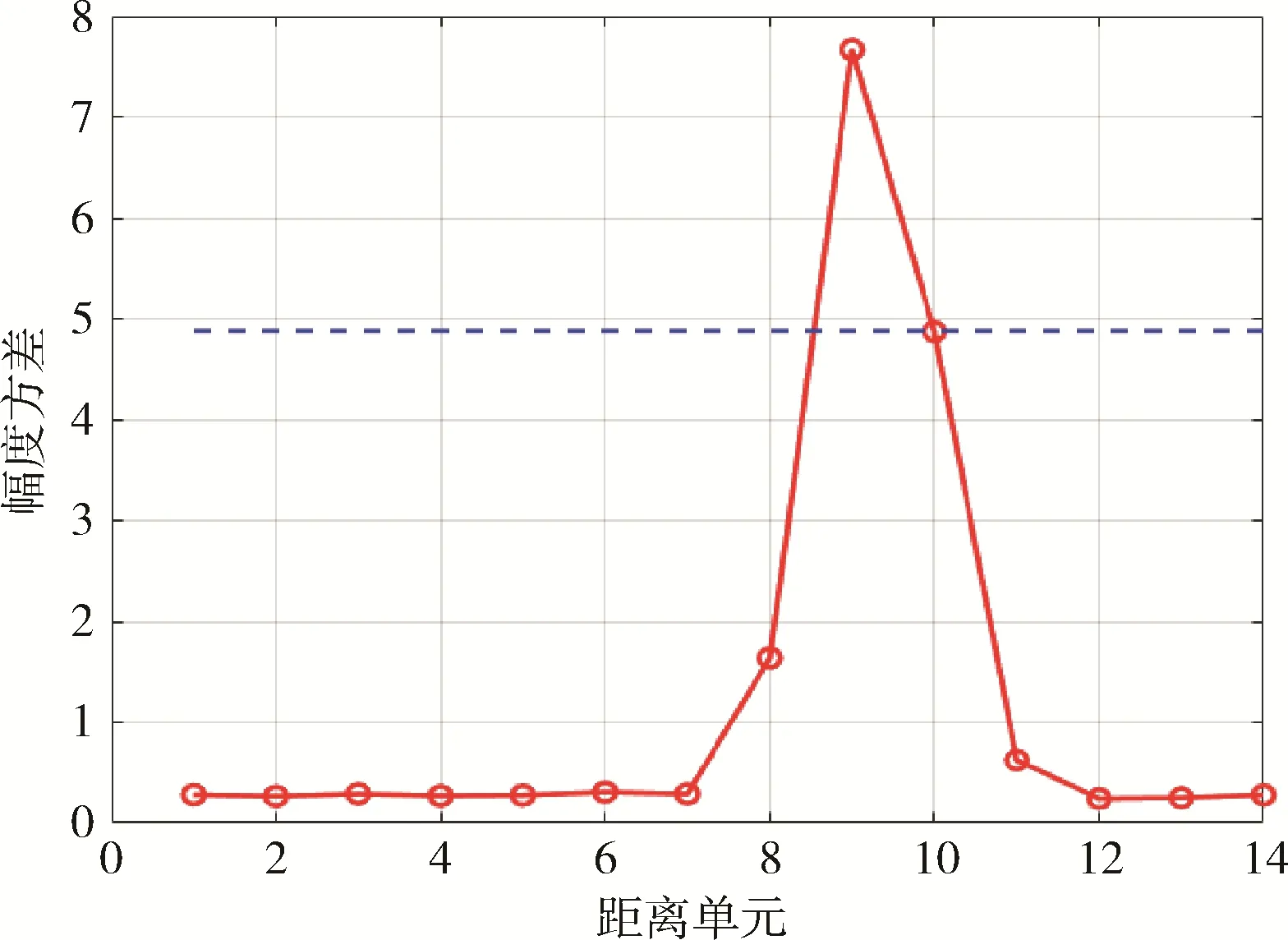
图2 幅度方差分布图

图3 高海况下的海杂波统计量分布情况

1.2.3 概率密度

概率密度是随机信号处理中的核心内容，用于描述连续型随机变量所服从的概率分布。国内外相关研究学者对IPIX 雷达的幅度分布进行了很多建模，目前主要的幅度概率密度分布模型有瑞利模型、威布尔模型和K分布模型。瑞利分布函数[5]为：

其中σ为形状参数，x为幅度。威布尔分布函数为：

其中p是形参，q是幅度参数。K 分布函数[6]为：

其中,F(v)是修正函数，a是形参，v是尺度参数。以第一组数据为例，幅度-概率密度分布模型如图4 所示。通过图4 可以看出，各类分布模型均有一个很长的“拖尾”现象。海洋环境复杂多变，对于海杂波统计特性建模，每种统计模型的拟合度都有一定的误差，而且普适性不强，但研究这些统计模型为构造海杂波特征向量提供了一些新的思路。

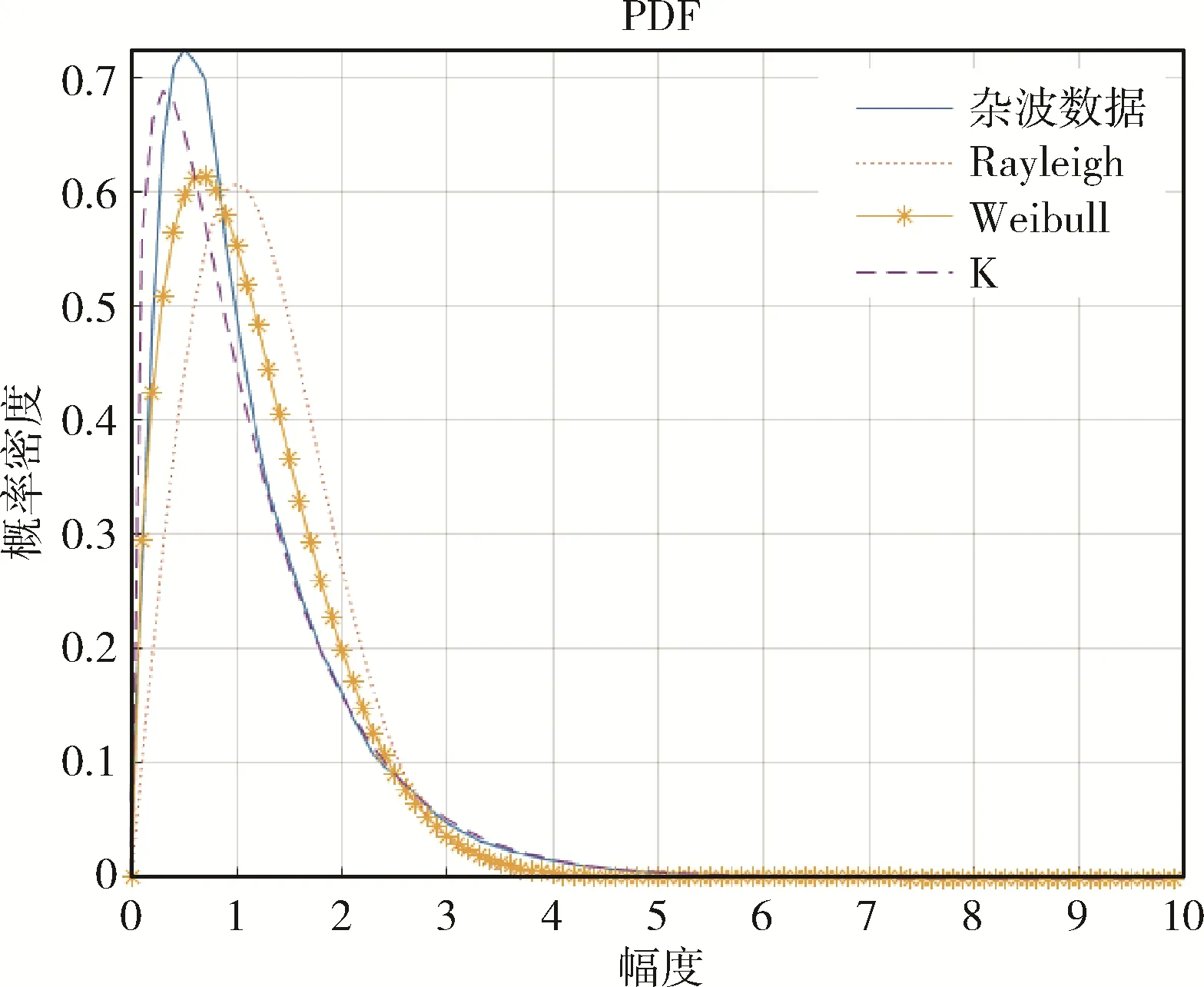
图4 海杂波幅度-概率密度分布图

综上所述，在海杂波与目标鉴别研究中，海杂波与目标的区分度受海况等环境因素影响较大。在低海况时，通过这些统计量的差异可以区分海杂波与目标。在高海况时，这些统计量并不能有效区分海杂波与目标。虽然这些常见的统计量在高海况下的区分度不理想，但是海杂波相关统计特性研究为寻找其他特征量提供了参考。

2 海杂波特征向量的构建

当今，海洋环境日益复杂，影响海杂波特性的因素复杂多样。海杂波在时域、频域、变换域等不同的维度表现出不同的特性。通过前文海杂波相关统计特性的研究，单一特征虽然对海杂波与海面目标有一定的区分度，但是仍然未达到直接鉴别的标准。在此基础之上通过构建多特征空间实现海杂波与海面目标的鉴别。海杂波分布具有随机性，信号幅度熵[7]越大所包含的幅度信息越多，目标相对于海杂波的幅度差异就越大。赫斯特指数(Hurst Exponent)[8-10]表征了海杂波序列的自相关性，在短时观测时赫斯特指数越大，目标与海杂波之间的差别越大，在一定程度上可有效区分目标与海杂波。而海杂波成因复杂，单一维度的特征无法更好地体现目标与海杂波间的差异，频域峰均比[11]表征了海杂波与目标在频域上的差异，在不同的海况下，目标与海杂波具有较为明显的区分度。因此，从时域和频域分析幅度熵、赫斯特指数、频域峰均比三种特征，构造能够有效区分海杂波与海面目标的特征向量空间。

2.1 幅度熵

幅度熵这个概念起源于信息熵，定义海杂波与海面目标在幅度上的差异为幅度熵。本节借鉴信息熵理论中的相关研究方法去描述海杂波与海面目标在幅度上的差异，构造出能区分海杂波与海面目标的一维向量。

对于IPIX 雷达实测数据，每一组实验数据容量均为131 072×14。首先，对每一个距离单元中的幅度序列X进行递增排序，每个距离单元中最大值为Xn，最小值为X1。然后将每个距离单元中的数据分成k个相互独立且长度相等的区间，统计每个距离单元中幅度落在每个区间的数量记为En并对其进行归一化处理。则幅度熵定义如下：

特别地，当第k个区间的幅值数目为零时，规定:Q(En)·log2Q(En)≡0，即IE(X)=0，避免出现某个区间幅值数目为零而导致对数运算出错。

在雷达极化方式和其他参数一定的条件下，以第一组实验数据为例，对不同距离单元下的幅度熵进行仿真实验，分别比较主目标单元、次目标单元幅度熵的差异，仿真结果如图5 所示。

图5 幅度熵分布图

由图5 可知，主目标单元和海杂波单元存在明显的断离现象，纯海杂波的幅度熵计算值集中在8.5 左右，目标的幅度熵计算值集中在9.8 左右。引入幅度熵这一概念，可将无序的海杂波信号通过随机信号处理变成有序的信号。由信息熵理论类比可知，幅度熵的计算值越大，所包含的幅度信息容量越大，复杂海洋环境下鉴别出海杂波与海面目标的概率越大。

在实际雷达凝视工作模式下，观测时间短。需要对观测时长做一定的处理，研究不同观测时长下的幅度熵，处理如下：对于海杂波幅度序列X，实验数据的观测时长为131.072 s，以2.048 s 为单位区间，单位区间与单位区间之间的重合度为m，则单位区间：

其中τ∈[1，131072]。根据区间的划分原则，提取1500个纯海杂波时间序列、1 500 个主目标单元时间序列，画出短时观测下的幅度熵散点图，如图6 所示。

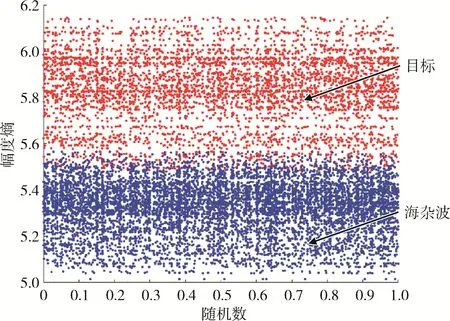
图6 幅度熵散点分布

由图6 可知，当观测时间较短时，海杂波与目标区分度也比较明显。更进一步说明海杂波与目标在幅度熵这一特性上有着十分明显的区分度，且区分效果不受观测时长的影响。因此，海杂波幅度熵可以作为区分海杂波与海面目标的一项重要特征。

2.2 赫斯特指数

目前，IPIX 雷达时间序列是学者们研究的热点，本文在海杂波时间序列方面也进行了相关研究。赫斯特指数是用来衡量时间序列是否有长期记忆的一个指标，体现了时间序列的自相关性，反映了序列中隐藏的长期趋势。

近些年来有研究学者将赫斯特指数引入到海杂波鉴别研究中，本节采用重标极差分析法来计算海杂波的赫斯特指数。对于每组海杂波实测数据，将131072 个时间序列按标定长度ψ划分为η段子序列，其中η子序列，定义为ηi，i∈[1,ψ]。对η中的数据按顺序依次定义为Xη,i，其离差为：

设Sη为Xη,i的标准差，那么子序列的标准差计算式为：

可得：

定义常数C和赫斯特指数H，使得不同距离单元下的重标极差与C、H满足：

因此，重标极差均值与赫斯特指数建立了一一对应的函数关系。以第一组实验数据为例，相关仿真结果如图7 所示。由图7 可以看出，海杂波与海面目标在赫斯特指数上具有很明显的差异。

图7 赫斯特指数分布图

对于海杂波幅度序列X，实验数据的观测时长为131.072 s，以2.048 s 为单位区间，单位区间与单位区间之间的重合度为m，单位区间如式（7）所示。根据单位区间的划分原则，提取1 500 个纯海杂波时间序列、1500个主目标单元时间序列，构建幅度熵-赫斯特指数的二维特征平面。以第一组实验数据为例，相关仿真结果如图8 所示。

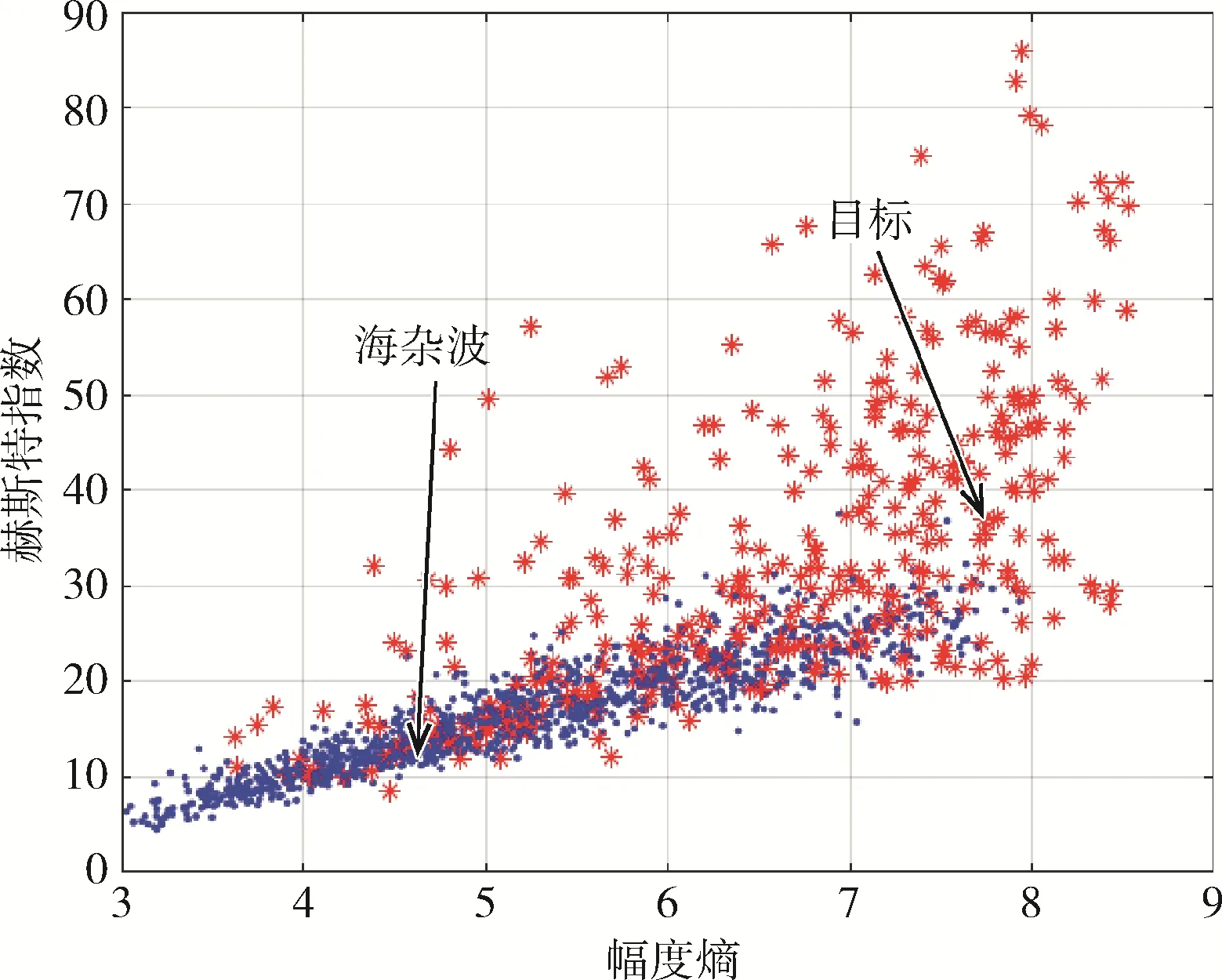
图8 赫斯特指数-幅度熵二维特征平面图

由图8 可以看出，在幅度熵-赫斯特指数平面上能在一定程度上区分海杂波与海面目标，但出现部分重合现象，因此仅仅通过幅度熵和赫斯特指数这两个维度不能精确区分两者。

2.3 频域峰均比

幅度熵与赫斯特指数都是从时域角度来提取海杂波统计特性的，海杂波与海面目标在两者构成的平面上有一定的重叠，频域分析往往能揭示时域不能描述的特征，两者形成互补，从而更全面刻画海杂波的特征。本节对海杂波实测数据的不同距离单元进行傅里叶变换，分析不同距离单元中幅度分布的相关特性，以频域中的幅度分布为基础，构建频域峰均比[15]这一特征向量。

首先对14 个距离单元进行傅里叶变换，处理方式如下：

式中，x(η)不同距离单元下的海杂波幅值，X(λ)为经过傅里叶变换后的频域中海杂波幅值，经过傅里叶变换实现了从时域到频域的转换。然后找出主目标单元中幅值的最大值max(X(λ))，求出其他纯海杂波距离单元中幅值的均值，定义频域峰均比的计算公式如下：

以第一组实验数据为例，其不同距离单元下的频域峰均比仿真图如图9 所示。通过图9 可以看出，不同距离单元下的海杂波频域峰均比中，主目标单元较纯海杂波单元区分度明显，而且主目标单元与混合单元的区分度也比较明显。

图9 频域峰均比分布图

2.4 特征向量的构建

通过仿真分析，幅度熵、赫斯特指数、频域峰均比这三个特征分量对海杂波均具有较好的区分度。然而，就单一特征分量而言，海杂波与海面目标的区分度并不是很高。特别是在高海况条件下，由于海尖峰的存在，仅仅利用单一特征分量并不能将海杂波与海面目标完全区分开。本节利用幅度熵、赫斯特指数、频域峰均比构建海杂波-目标的三维特征空间，以第一组、第二组实验数据为例，仿真结果如图10 和图11 所示。通过图10 和图11 可以看出，海杂波与海面目标在三维特征空间中的分布均比较集中，具有较为明显的区分度。

图10 海杂波三维特征空间

图11 海杂波三维特征空间

3 卷积神经网络设计与鉴别研究

3.1 海杂波训练数据库的建立

本文研究的10 组实验数据容量均为131 072×14，在建立训练数据库时，首先对10 组数据的不同距离单元进行幅度熵、赫斯特指数、频域峰均比的计算，其中目标距离单元记为1，海杂波距离单元记为0，这样每个距离单元就变成了一个131 072×4 的矩阵，将该矩阵转化为Excel 表格，这样就形成了训练数据总库，按随机抽样原理，抽取时，目标距离单元和海杂波距离单元按1:4 的比例随机抽取，对每一组实验数据随机抽取4 000 个作为训练数据，一共10 组，形成训练数据库，部分训练数据库如表2 所示。

表2 海杂波训练数据库（部分）

3.2 卷积神经网络

1995 年Yann LeCun 和Yoshua Bengio 引入了卷积神经网络[13],CNN 是一种基于数学卷积运算的多层神经网络，利用输入数据间存在的关联，提取数据特征并提高整体训练性能，被广泛应用于各类分类识别研究中。由于CNN 能同时进行特征提取和鉴别，并伴随着训练而产生无需手动选取特征，并自行进行分类鉴别，而且鉴别精度优于其他机器学习方法。因此，CNN 有着更为广泛的应用前景。

CNN 主要有训练和鉴别这两个工作过程，通过卷积层对实验数据进行特征提取，形成有规律的映射，经过池化层的向下采样，简化网络结构，减少特征参数，完成算法优化，然后运用训练出来的模型进行分类鉴别研究。

卷积神经网络一般由输入层、卷积层、池化层、全连接层和输出层组成。输入层是数据输入层，主要用于存储接收待研究的数据。CNN 接收到实验数据后，利用卷积层中卷积核的权重比对输入数据进行数学卷积运算处理，计算公式如下：

当卷积层完成实验数据的特征提取后，需通过池化层继续优化，如去除冗余的特征信息、简化CNN 模型和提高算法效率。CNN 中池化方法有均值池化（average pooling）和最大值池化(max pooling)这两种方法，本节采用最大池化法对实验数据进行池化处理，具体处理过程如下：

全连接层是将所有训练数据的特征汇总到一起，将各特征信息按一定的权重求和，然后经激活函数运算将结果传送到输出层，其相应数学原理如下：

其中，f是该全连接层t的激活函数，at为全连接层t的权值比例系数，wt是该层的偏置量，μt是特征信息按照一定的权重并通过数学偏置运算而得到的。

输出层是输出鉴别结果的功能层，本文是区分海杂波与海面目标的二分类问题，输出层采用Sigmoid 激活函数，当输出一个鉴别精度时，可通过输出的鉴别精度不断调整特征参数，保证在算法复杂度不变的条件下鉴别精度最高。

3.3 基于训练数据库的卷积神经网络设计

本节基于IPIX 雷达实测数据，根据所建立的海杂波-目标数据库，设计海杂波-目标卷积神经网络。设计总体思路和流程图如下：首先对海杂波-目标数据库进行相关处理形成变量矩阵，对变量矩阵进行拟合、数据格式转换，最后完成CNN 模型的建立。在建立CNN 模型时，首先设计单层卷积神经网络，卷积核大小为2，滑动步长是1。然后设计线性层，线性层中包含了一个隐藏层，该隐藏层里面有10 个神经元节点，并运用droput正则化[14]的方法，来增加学习速率、避免出现过拟合的问题，大大提升了CNN 模型性能。完成卷积神经网络设计后，海杂波与目标的鉴别大致分两个阶段，第一阶段是通过训练数据库训练出海杂波与海面目标分类识别模型，第二阶段是利用检测数据库检验海杂波-目标分类识别模型的鉴别精度，设计思路如图12 所示。

图12 CNN 网络设计思路流程

在进行CNN 训练模块的设计时，将80%实验数据进行计算处理，最后形成训练模型。用实验数据库中20%的数据作为检验数据库，根据输出结果来判断设计训练模型的好坏，形成闭环反馈机制，并适当调整训练模型参数，提高鉴别精度，使其满足设计要求。

CNN 设计流程:

(1) 初始化

导入Python 中numpy 和torch 等库。导入实测数据，制作仿真数据集，并将数据转换为张量格式。

(2) 定义预测函数mode1。

(3) 建立CNN 模型，每个卷积层中输入卷积核in_channels=1，out_channels=16，卷积核大小kernel_size=2，卷积步长stride=1。

(4) 通过CNN 训练鉴别模型。

(5) 计算鉴别精度，Pξ计算公式为：

(6) ifPξ＞Pλthen

(7) 输出鉴别精度Pξ

(8) else return 优化器。

(9)Tξ=Tξ-T0

(10) batch_size=batch_size-100

(11) whilePξ＞Pλ

(12) end while

printPξ

4 海杂波仿真实验分析

本节对海杂波实测数据库进行仿真分析，从鉴别精度和算法复杂度两个角度比较CNN 与传统支持向量机算法[15-16]、层次分析法[17]的优劣，对比得出最佳的海杂波与目标鉴别方法。

信噪比表征信号测量的精度，信噪比越大测量越有效，测量结果越准确。结合本实验IPIX 雷达工作模式和试验时的海情状况，从频域分析信噪比，首先对时间序列进行傅里叶变换，增加目标的特征幅值，抑制了海杂波噪声幅值，提高了信噪比。由此计算IPIX 实测数据的平均信噪比，各组平均信噪比分布如图13 所示。

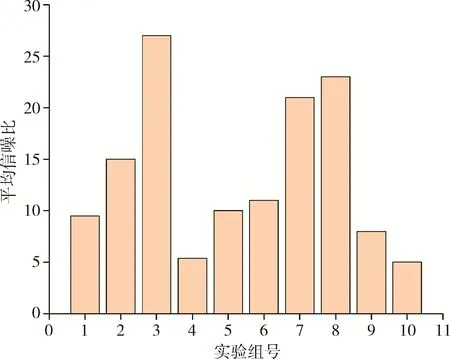
图13 平均信噪比分布图

在此基础之上，研究不同平均信噪比条件下的鉴别精度，仿真结果如图14 所示。由图14 可以看出，CNN 算法和SVM 算法鉴别精度均集中在90%左右，总体鉴别精度很高，特别是对于目标特征信号不明显、平均信噪比比较低的组别，CNN 也有较高的鉴别精度。而AHP法鉴别精度在65%左右波动，比前两种算法精度低得多，AHP 法通过求取权重系数，设置固定门限来鉴别海杂波与目标，且权重系数不随实验组数变化而改变，相比前两种算法，没有较好的自适应性。

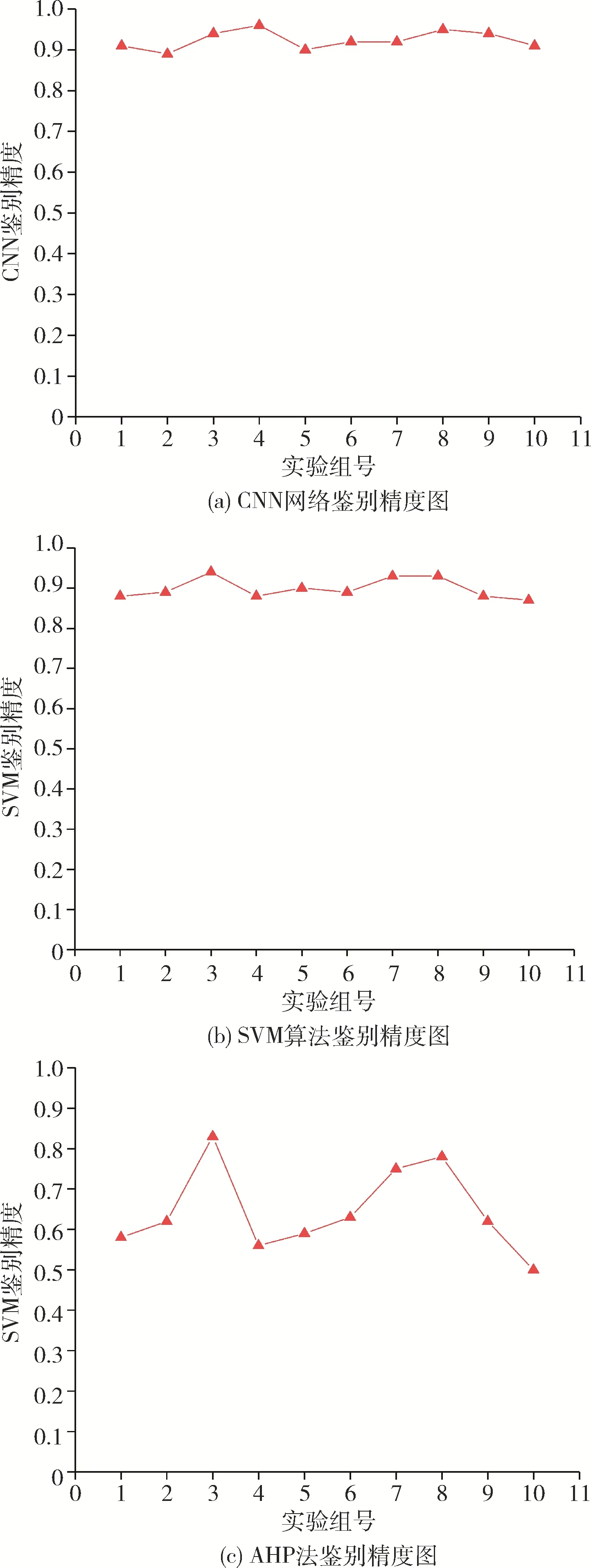
图14 不同平均信噪比条件下的鉴别精度

由图15 可以看出，三种算法的鉴别精度均随平均信噪比的增加而增加，相比SVM 算法，CNN 精度提高10%以上。而AHP 算法，总体鉴别精度比CNN 算法和SVM算法较低，这是由于AHP 算法鉴别门限设置的随机性较大的原因造成的。

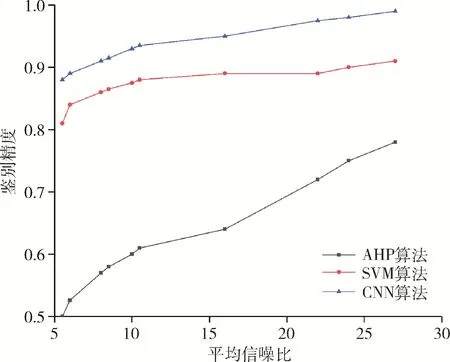
图15 三种方法综合比较图

算法复杂度包括时间复杂度和空间复杂度，时间复杂度主要体现在算法运行时间的长短，算法空间复杂度主要体现在算法运行过程中所占储存空间的大小。由表3 知，在算法平均运行时间上，CNN 用时最少，同时，CNN 所占存储空间最小。所以，在算法复杂度上CNN相比其他方法较为简单。

从数据利用的充分性上，AHP 法需要利用所有的实验数据，并且在数据处理时耗时长、计算复杂。SVM 算法和CNN 一样，都需要利用训练数据库进行特征提取、训练模型，然后再检验模型的准确性，但 SVM 算法参数多，调试复杂，运行耗时长，CNN 参数少，运算时间短。综合比较，CNN 优势明显。

5 结论

本文通过分析IPIX 实测数据，构建由幅度熵、赫斯特指数和峰均比组成的特征向量，仿真结果表明海杂波与目标在特征空间中区分度明显，并由此形成训练数据库，最后结合训练数据库特征，设计卷积神经网络进行鉴别研究，并与传统支持向量机算法和层次分析法进行比较，分析表明设计的CNN 在海杂波鉴别研究中鉴别精度高，能有效鉴别海杂波与目标。