一种改进的干涉仪-MUSIC联合测向算法

2023-12-04姚志成许佳诺王海洋

兵器装备工程学报 2023年11期

姚志成,许佳诺,杨剑,王海洋

(火箭军工程大学导弹工程学院, 西安 710025)

0 引言

目标信号角度估计也称为测向,测向技术早在20世纪60年代,人们就开始尝试研究,应用在各种领域当中,到目前为止,各种测向技术发展成熟。常用的方法有多通道比幅测向、时差测向、相位差测向及空间谱测向等,其中相位干涉仪测向法和MUSIC测向法是最常用的测向方法之一。

相位干涉仪测向应用广泛,其测向精度高、测向速度快、技术成熟、覆盖频段宽。常见的相位干涉仪按天线阵布阵形式主要分为一维、二维和三维干涉仪。一维干涉仪测向法通常包括虚拟基线法[1]、参差基线法[2]、长短基线法[3]等;二维干涉仪包括“L型”天线阵、“T型”天线阵、正交“十字型”天线阵、均匀圆阵[4]、旋转基线法[5]和双基线旋转法[6]等;三维干涉仪测向法包括立体基线法[7]等,其中,圆阵干涉仪具有较高的解模糊概率和较高的测向精度,比起均匀线阵与均匀矩形阵,在相同孔径渡越、低阵元数的条件下,均匀圆阵具有最优的尺寸、全方位的测向能力,广泛的应用于电子侦察领域[8-10]。均匀圆阵具有圆对称性,在阵元数较多时,各向分辨能力近似相等,同时,其是一种平面阵,具有二维空间角的测向能力。因此,均匀圆阵更适用于测向信号接收系统[11]。文献[11]以均匀圆阵为基础,分析论证了阵元数为奇数的均匀圆阵相比于阵元数为偶数的均匀圆阵测向精度更高、各向等效性更好、抗相位模糊能力更强,同时五阵元均匀圆阵是无模糊均匀圆阵中阵元数最少的,因此具有更好的经济实用性。与常见的干涉仪测向方法相比,相位干涉仪[12-13]测向方法存在硬件通道不一致、相位模糊等问题,降低了方位检测性能;相关干涉仪[14-15]测向方法是利用来波信号的相位差与相位差库中的相位差做相关运算处理取最优值进行测向,其算法运算较为简单,但测向精度不高、角度分辨力较差,且受相位差库的质量影响较大。在使用阵列天线进行干涉仪测向时,由于遮挡等因素会削弱某些阵元所接收的信号,从而增加相位误差,为了解决此问题,文献[16]计算了信号接收较强的阵元所估计的相位差,以此来推算并代替信号较弱的相位差。为了提高干涉仪测向速度,文献[17]提出了利用俯仰角间隔采样的方法降低了计算复杂度,得出了10°和20°为采样间隔时系统采样难度小、测向有效区域较大、计算复杂度较低的结论。在干涉仪测向中,俯仰角的大小会影响测向精准度,文献[18]提出维度分离方法,在二维样本中,随机选择俯仰角进行方位角搜索,再使用方位角搜索俯仰角,此方法能够有效减小俯仰角数值对测角精度的影响,但仅仅适用于无相位模糊的情况下。

MUSIC算法[19]是阵列信号处理领域的主要发展方向,该技术可以很大程度提高角度估计精度、角度分辨力及其他相关参数估计精度,因而在声纳、通信、雷达等领域有着广泛的应用,但其复杂的运算不能满足工程实时性需求。为了提高运算速度,文献[20]提出了利用误差补偿对空间域分量进行修正,结合MUSIC测向算法,构造四维极化敏感阵列空间谱函数的方法,通过降维谱峰搜索可实现来波信号的二维测向,该算法相比于传统MUSIC减小了运算量。文献[21]分析了美国NAVSPASUR系统交叉干涉仪测向所采用的逐次解模糊算法及其性能,提出了一种用于交叉干涉仪测向的MUSIC算法,该算法从根本上克服了错误解模糊带来的测角误差的波动,保证了测向过程的稳健性,从而提高了干涉仪测向系统的鲁棒性。文献[22]在二维谱峰搜索过程中引入遗传算法降低了均匀圆阵MUSIC算法的谱峰搜索时间。文献[23]将干涉仪测向法对来波信号的初测角分别以俯仰角和方位角为中心上下各取10°范围进行MUSIC算法的谱峰搜索,既相对于MUSIC算法减小了计算量又相对于干涉仪测向法提高了测向精度,但是当干涉仪测向法所测角度误差大于10°时,该算法则失效。文献[24]与文献[23]类似,将干涉仪测向法对来波信号的初测角分别以俯仰角和方位角为中心上下各取5°范围进行MUSIC算法的谱峰搜索,达到了减小计算量和提高测向精度的效果,但是当干涉仪测向法所测角度误差大于5°时,该算法则失效。文献[25]提出了基于加权最小二乘法和MUSIC算法相结合的被动测向技术,改进后的干涉仪测向法联合MUSIC测向法,相比于传统MUSIC测向法减小了搜索时长,相比于文献[23],具有较高的初始角测量精度,但是该方法同文献[23]和文献[24]类似,由于信噪比较低等原因使得初始角测量值误差较大且大于10°或5°时,同样导致测向失效。

针对以上问题,文章结合干涉仪测向法的测向速度较快和MUSIC测向法的测向精度较高的优点,基于误差分析,提出一种能够同时提高测向速度和精准度的干涉仪-MUSIC联合测向算法,相比于文献[25],文章所提算法的测向速度更快,并且对不同初始角测向误差具有更强的适应性和鲁棒性。

1 算法原理及天线排布

1.1 基于最小二乘法的相位干涉仪测向算法

本节首先介绍一维单基线二阵元测向原理,其基本原理是利用平面波信号在一条测向基线上路程差引起的相位差与辐射源来波方向的显式关系,通过解方程得到信号的方向。二阵元单基线阵相位干涉仪测向系统的组成及信息流向示意图如图1所示。

设入射信号波长为λ,天线A1与A2间距为d,来波角度为α,2个天线接收信号的相位差为

φ(α)=(2πd/λ)sinα

(1)

文章取d/λ<1/2,即天线阵基线长度小于半波长时无测向模糊问题,此时:

α=arcsin(φλ/2πd)

(2)

对于二维测向,需要测得方位角和俯仰角,当天线布阵一定时,在无测向模糊的情况下所测得的测角值与天线相位差产生一一对应的关系。根据天线建立理论相位差库,在实际测得相位差后,采用最小二乘法与理论相位差库作比较,寻找最为接近即差值最小的相位差,该相位差所对应的角度为所测目标角度。为了提高准确性,干涉仪测向法通常采用多基线获取不同的相位差,取其中的最优值。文章建立以半径为r的5阵元天线均匀圆阵,建立均匀圆阵测向坐标系如图2所示。

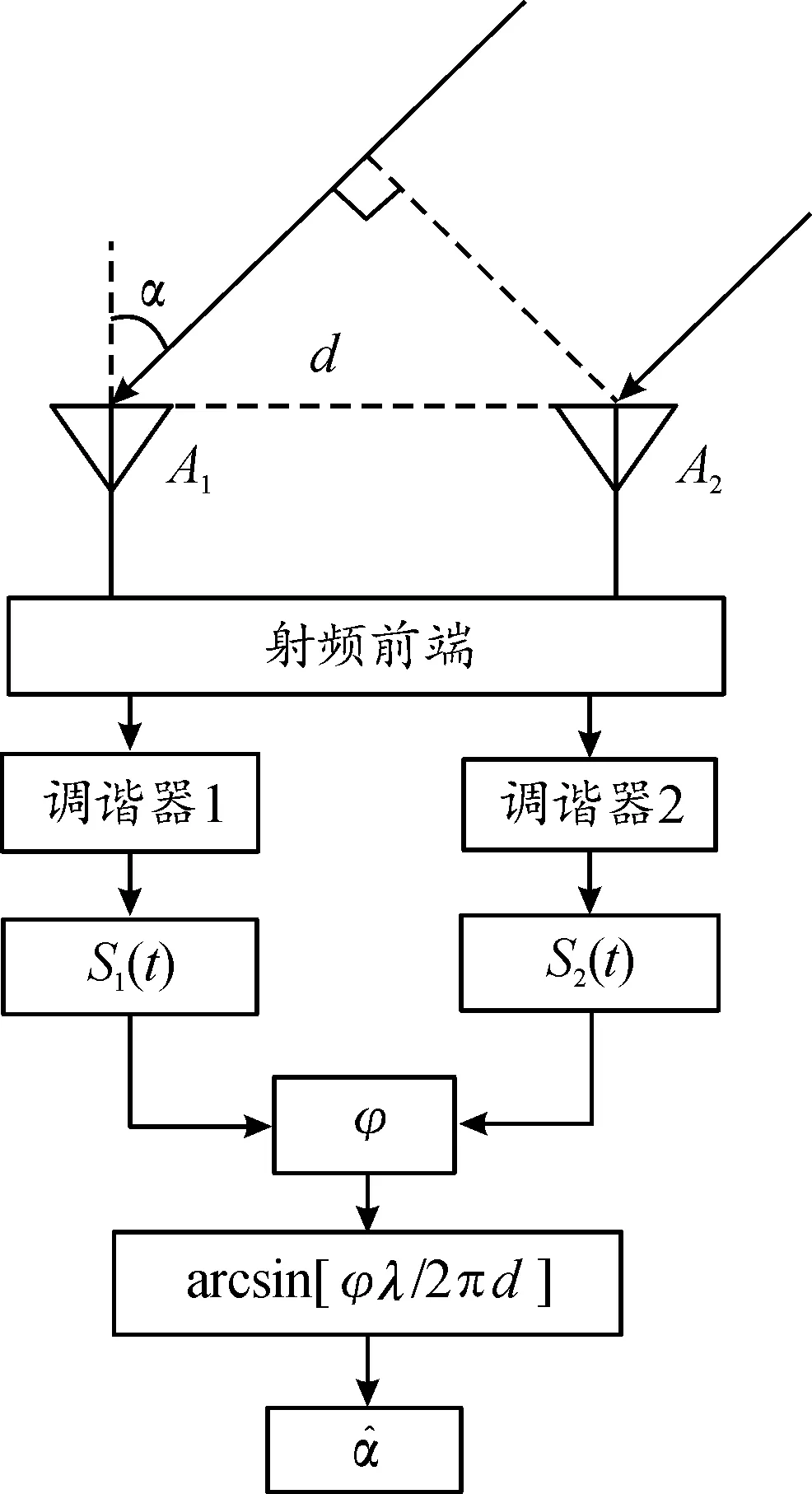
图1 二阵元单基线阵相位干涉仪测向系统的组成及信息流向Fig.1 Composition and information flow of the direction- finding system of two-element single-baseline phase interferometer

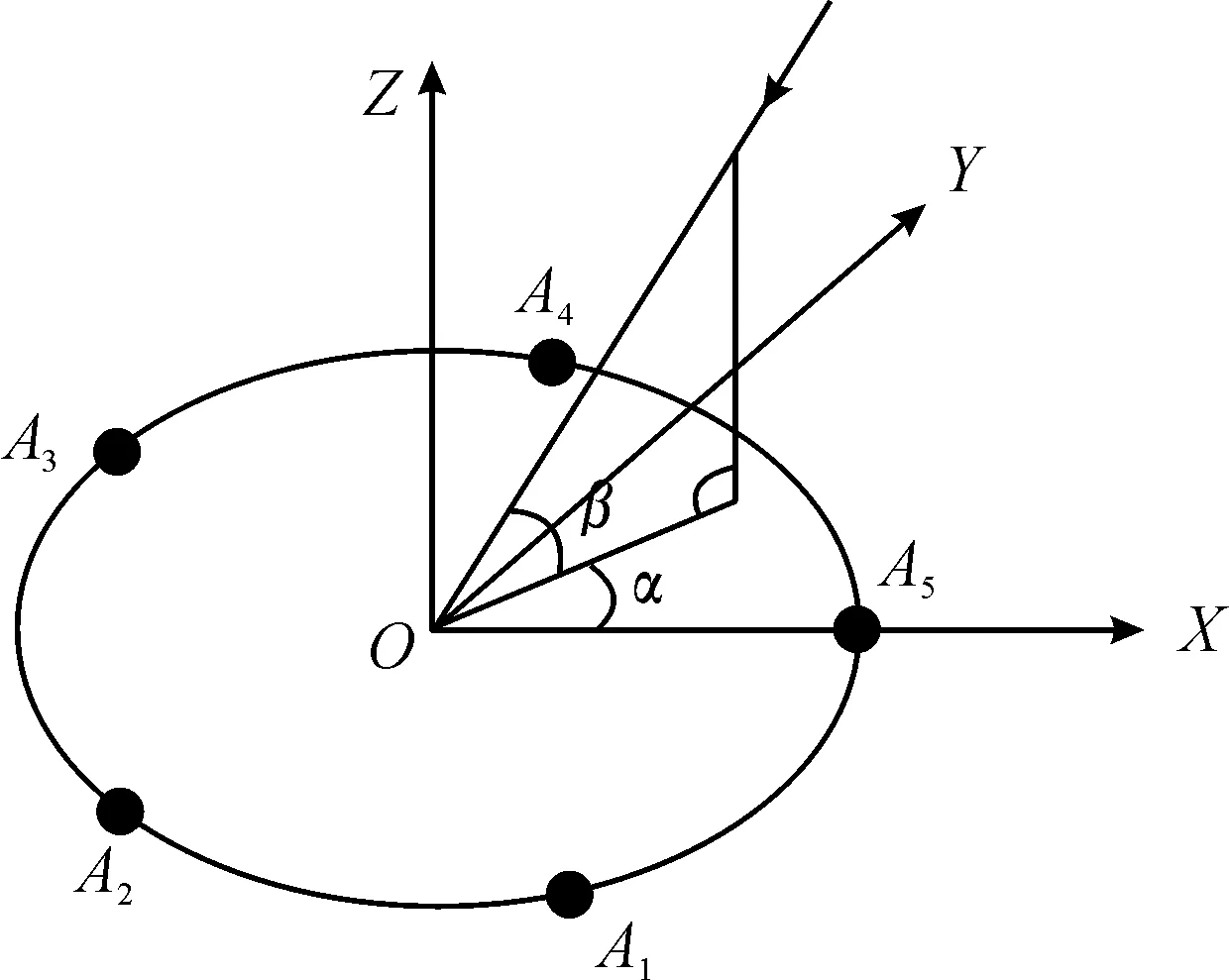
图2 均匀圆阵测向坐标系示意图Fig.2 Schematic diagram of uniform circular array direction finding coordinate system

在图2所示的均匀圆阵中,圆心O为参考点,相对于O,第n个天线阵元处接收到的信号相位为

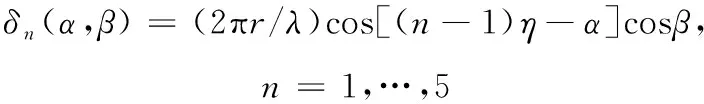
(3)

式(3)中:r为圆阵半径;λ为信号波长;η=2π/N为将圆周2π被阵元数均分后的角度,其中N=5为阵元数。用矢量可以表示为

δ(α,β)=(δ1(α,β),…,δN(α,β))T

(4)

(α,β)的广义最小二乘估计为

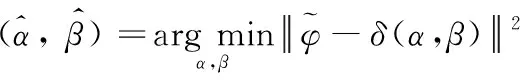
(5)

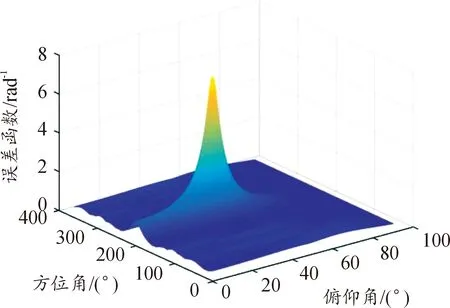
图3 误差函数的三维图Fig.3 Three-dimensional diagram of error function

1.2 MUSIC测向算法

设入射角为(α,β)时的方向矢量为a(α,β),a(α,β)可表示为

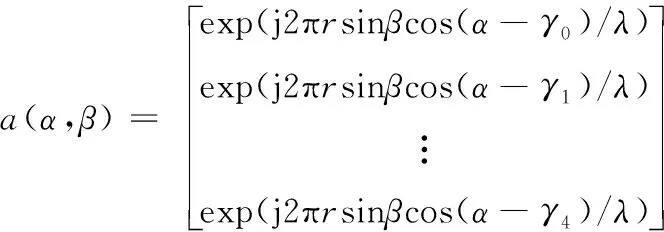
(6)

式(6)中:γm=2πm/5,m=0,1,…,4;r为圆阵半径;λ为信号波长。

设阵列输出信号为X(t),其协方差矩阵为R=E{X(t)X(t)H},对协方差矩阵R进行特征分解得:

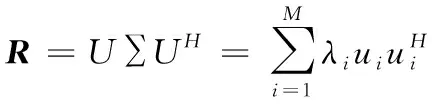
(7)

构造阵列空间谱函数:

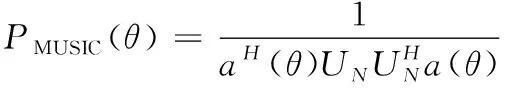
(8)

通过搜索波峰来估计波达角。由于传统的MUSIC测向算法在0～360°全域范围内搜索来波方向,计算量巨大,计算时间过长,导致测向速度缓慢,不能够满足工程需求。

2 相位干涉仪测向法误差分析

由式(3)可知,影响信号来波方向角度因素有各阵元接收信号相位误差、阵元位置误差、信号波长估计误差和来波方向的方位角和俯仰角等。在本章中认为各阵元接收信号相位误差、阵元位置误差和信号波长估计误差较小,可忽略不计,针对方位角和俯仰角对测向的影响作以如下分析。

设第n1个和第n2个阵元接收到的信号相位分别为

δn1(α,β)=(2πr/λ)cos[(n1-1)θ-α]cosβ

(9)

δn2(α,β)=(2πr/λ)cos[(n2-1)θ-α]cosβ

(10)

对δn1和δn2分别求全微分得

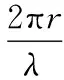
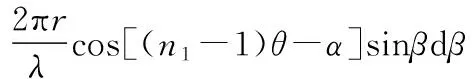
(11)

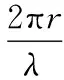
(12)

由式(12)可得

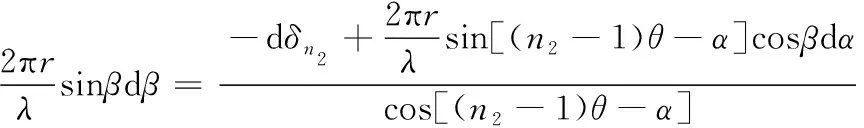
(13)

将式(13)代入式(11)得

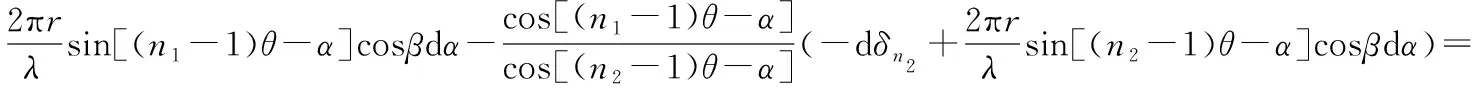
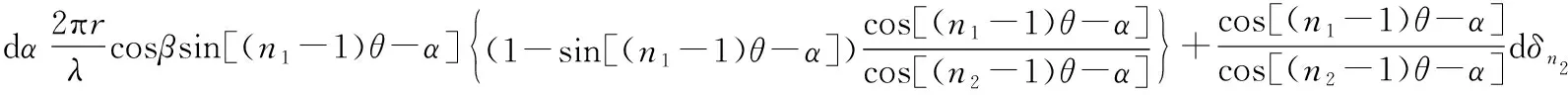
(14)

由式(14)得:

(15)

由式(15)可以看出,当其他条件不变时,dα随β由0～90°范围内增大而增大,同样方法可得,dβ随β由0～90°范围内增大而减小。α和β随俯仰角变化的均方根误差仿真结果如图4所示。对均方根误差进行最小二乘拟合,方位角α和俯仰角β拟合函数分别为:

αRMSE=3×10-9β6-7×10-7β5+6×10-5β4-

0.002 7β3+0.057 4β2-0.501 5β+1.905 2 (16)

βRMSE=-3×10-10β6+7×10-8β5-8×10-6β4+

0.000 3β3-0.003β2-0.173 4β+5.053 9

(17)

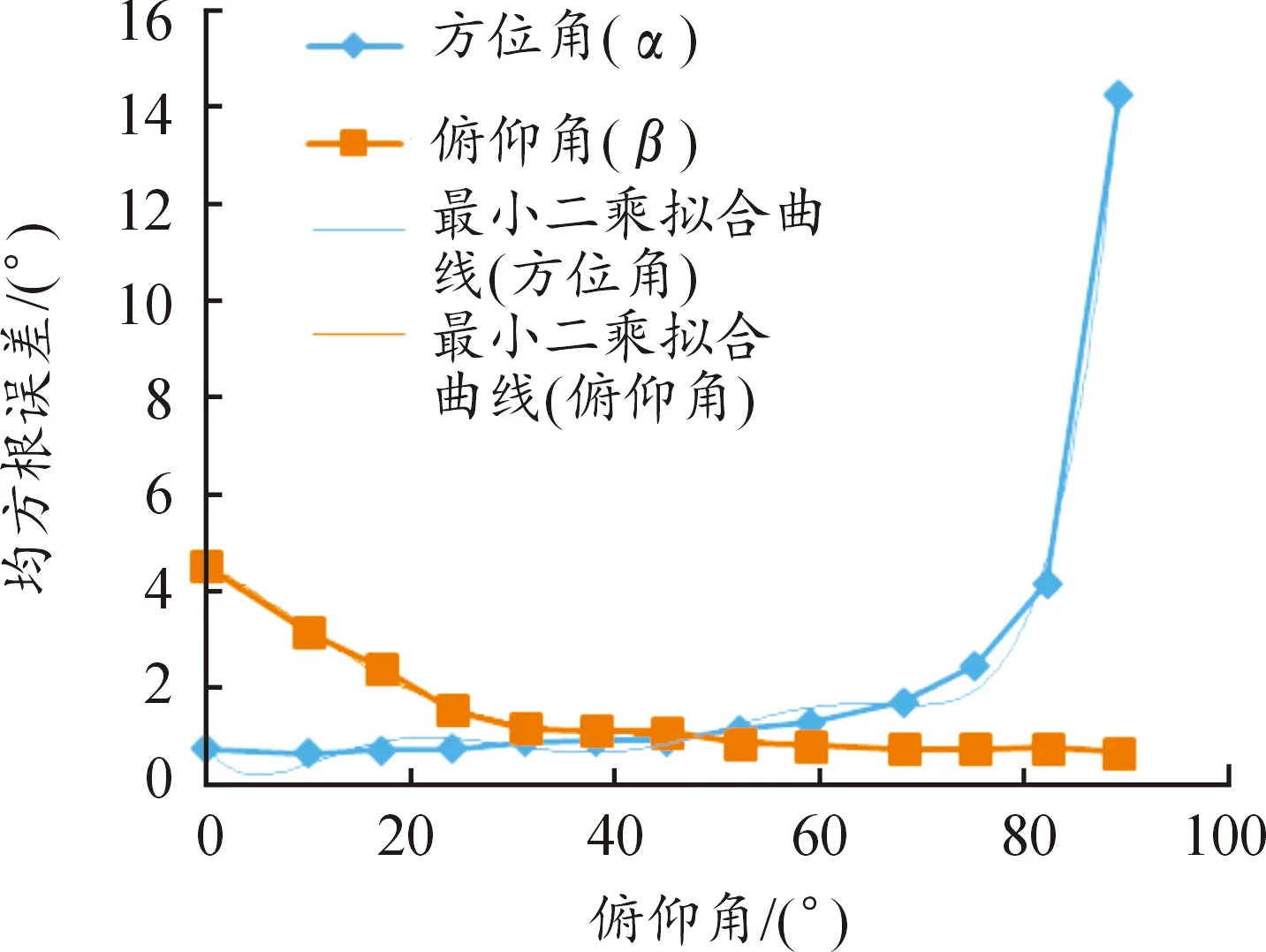
图4 来波方向角度均方根误差及拟合函数曲线Fig.4 Curve diagram of root mean square error and fitting function of incoming wave direction angle

由于阵型为五阵元均匀圆阵且水平放置,所以当来波信号的俯仰角不变,方位角在0～360°范围内任意角度变化时,入射信号真实方向角度与所测方向角度之间的均方根误差不会受方位角大小的影响,α和β随方位角变化的均方根误差仿真结果如图5所示。

图5 来波方向角度均方根误差曲线Fig.5 Root mean square error curve of incoming wave direction angle

3 算法改进

3.1 改进相位干涉仪测向法

相位干涉仪测向法是在相位差库中对方位角360°和俯仰角90°范围内遍历搜索,以其与真实方向测得的相位差误差作为代价函数,当相位差误差取最小值时,所对应的波达角可认为真实方向角。然而,遍历搜索运算量较大,因此本节提出一种简化计算量的方法。由图3可以看出,在俯仰角方向上,误差函数图的主体部分分布20°以上,所以无论方位角和俯仰角取何值,在俯仰角方向上以10°为间隔划分时,总能在误差函数图上找到明显峰值。并且,文献[17]得出了俯仰角以10°或20°划分采样间隔能够有效测向并减小运算量的结论。由于所采用的阵型为均匀圆阵,由图5可知,方位角的大小不会对计算结果产生有规律性的影响,并且在真实方位角两侧产生的相位误差几乎对称,所以当在真实俯仰角附近取固定值计算相位差误差时,其最小值对应的方位角可认为是真实方位角,即在误差函数图的峰值处对应的方位角可认为是真实方位角。

具体步骤如下:

1) 在俯仰角90°范围内以10°为间隔等角度划分,产生10个俯仰角度值分别为0°、10°、20°、30°、40°、50°、60°、70°、80°、90°。

2) 在相位差库中提取以该10个俯仰角度值对应的所有方位角的相位差。

3) 测量真实方向的相位差,并与步骤2)提取的相位差进行最小二乘运算。

4) 选取运算结果最小值,其所对应的方位角可认为真实方向的方位角。

5) 在相位差库中提取以步骤4)所得方位角为固定值对应的0～90°范围内仰角的相位差。

6) 真实方向信号的相位差与步骤5)提取的相位差进行最小二乘运算。

7) 选取步骤6)运算结果最小值,其所对应的俯仰角可认为真实方向的俯仰角。

假设以0.1°为步进搜索,遍历搜索的运算量为3 601×901次,而通过上述步骤,可以将运算量减少至10×3 601+901次,能够有效提高运算效率。图6为步骤4)结束后的误差函数图,最高点为10个固定俯仰角产生的相位差误差最小值处,其所对应的方位角可认为真实方向的方位角。图7为步骤7)结束后的误差函数图,其最高点为方位角固定后运算的相位差误差最小值处,其对应的俯仰角可认为真实的俯仰角。

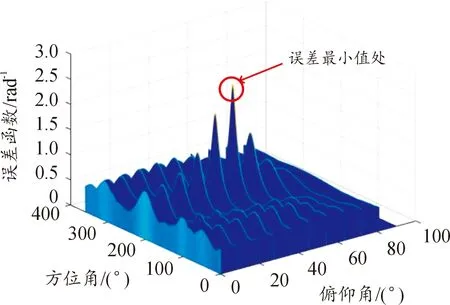
图6 步骤4)结束后的误差函数图Fig.6 Figure of error function after step 4)

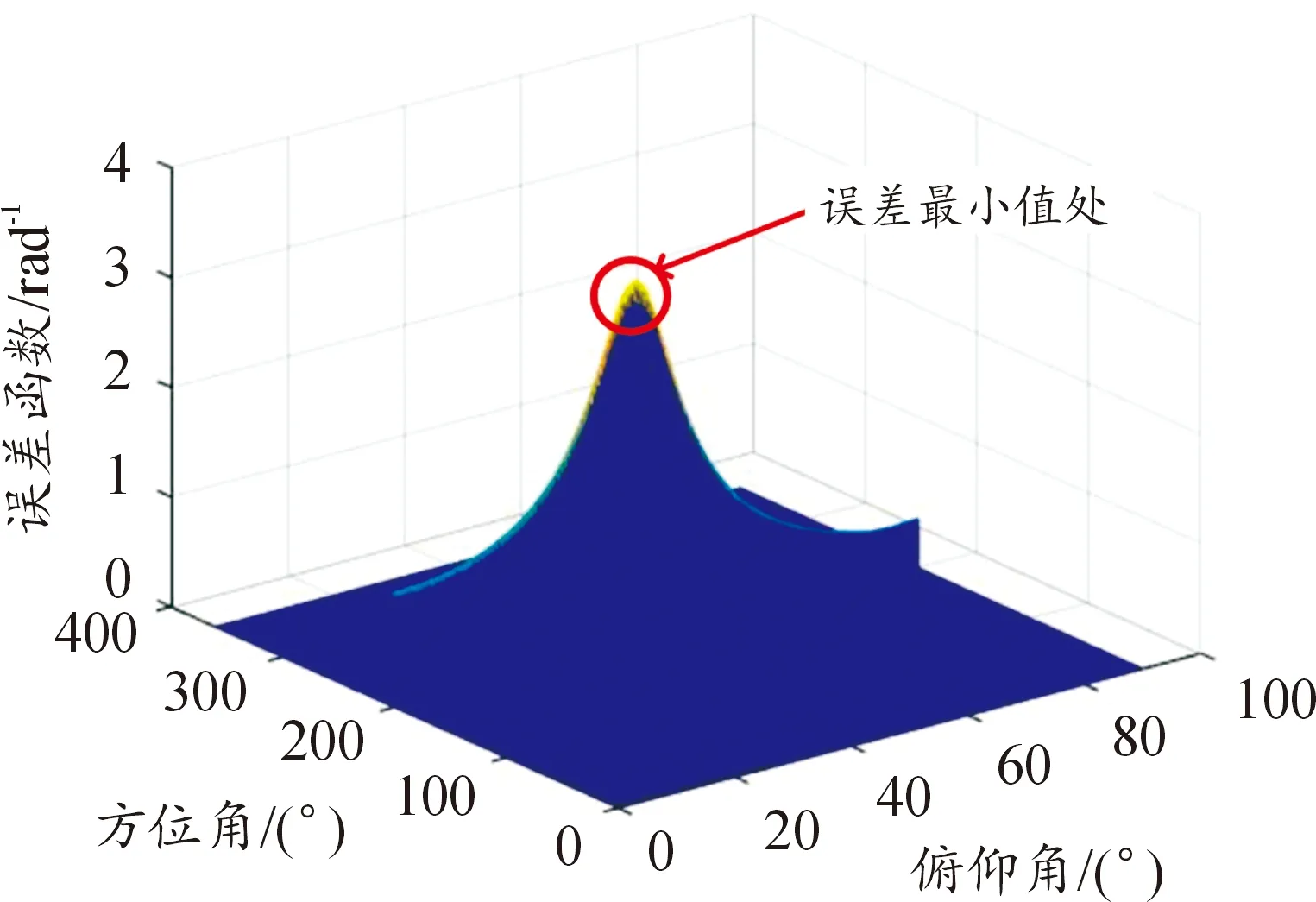
图7 步骤7)结束后的误差函数图Fig.7 Figure of error function after step 7)

3.2 改进后的干涉仪和MUSIC联合测向法

干涉仪测向法的优势在于测向速度快,而测向精度不高,MUSIC测向法优势在于测向精度高,而测向速度慢,因此本节提出将4.1节改进后的干涉仪测向法与MUSIC测向法结合,从而同时提高测向速度和精度。具体步骤如下:

1) 利用4.1节算法步骤,测得方位角和俯仰角的初始值。

2) 根据步骤1)所测初始角度分别在方位角和俯仰角2个维度上选择搜索范围。

3) 在步骤2)选取的角度范围内利用MUSIC测向法搜索,提高测向精度。

在步骤2)中,搜索范围的选择应根据第三章对相位干涉仪测向法进行误差分析的结果而定,根据最小二乘拟合结果选取搜索范围,误差大则选取范围大,误差小则选取范围小,以此来保证在俯仰角0°～90°范围内具有较高的测向精度。

整体算法流程如图8所示。

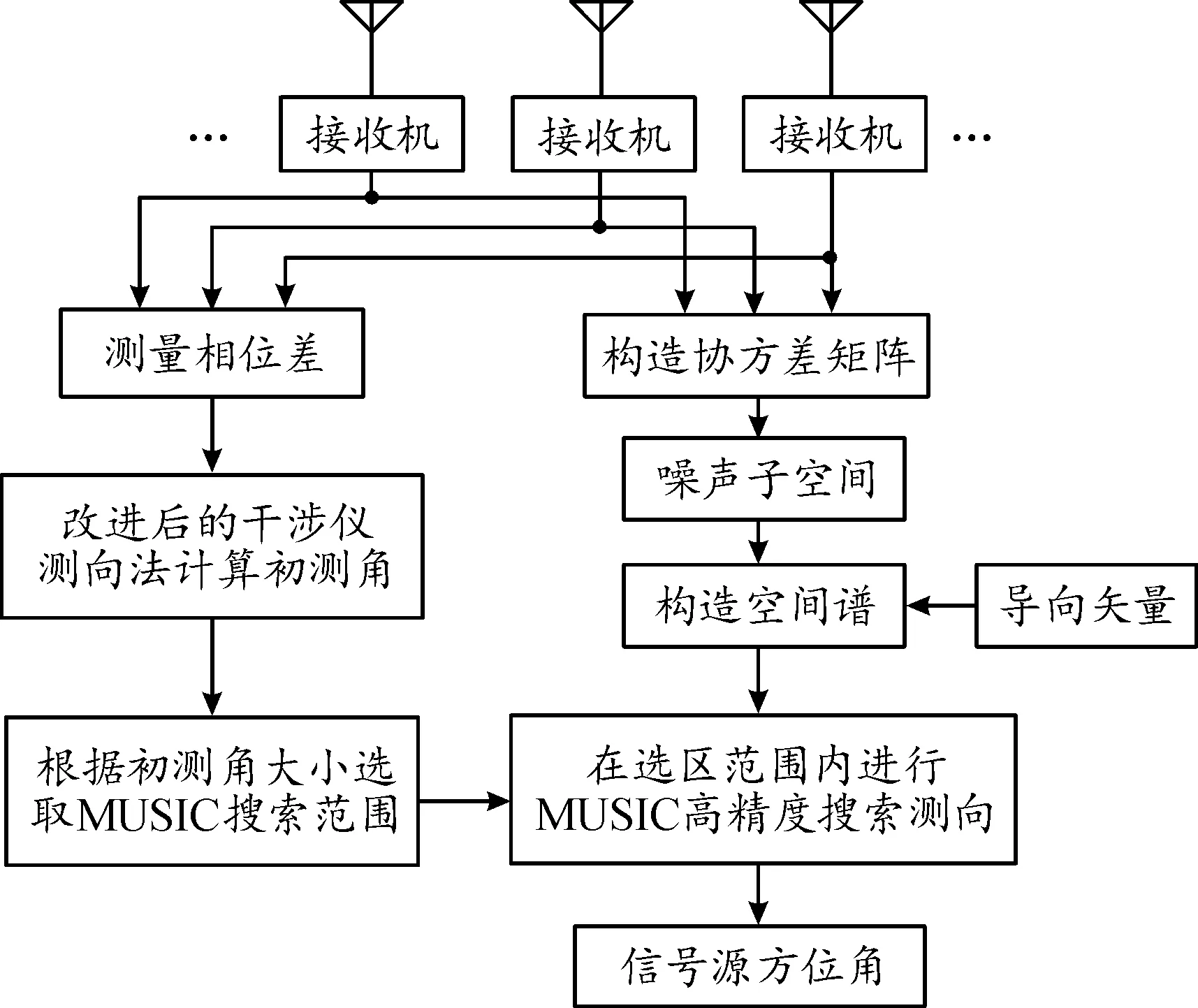
图8 算法流程图Fig.8 Algorithm flow chart

4 算法仿真

为检验文章所提算法的有效性,将本文中算法与传统干涉仪测向算法、MUSIC测向算法以及文献[25]所提算法的仿真结果进行比较。主要分为2大部分,一是测角精度比较,二是测角耗时比较。具体设计了如下仿真:① 4种算法的均方根误差与信噪比的关系;② 4种算法的均方根误差与方位角变化关系;③ 4种算法的均方根误差与俯仰角变化关系;④ 4种算法的耗时比较。仿真阵型为均匀圆阵,圆阵半径为0.1 m,阵元数为5,信号频率为2.4 GHz,入射信号方位角为200°,俯仰角为40°,仿真工具为Matlab R2016a。

4.1 测角精度比较

为了衡量不同测向算法对信号源测向估计的精度,定义入射角估计均方根误差为

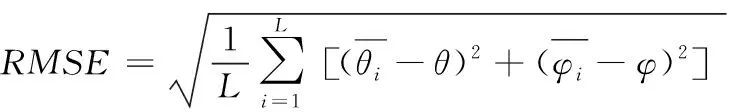
(18)

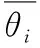
仿真1:4种算法的均方根误差与信噪比的关系

为了比较4种算法在相同仿真环境下不同信噪比对测向误差的影响,文章仿真了在信噪比从-10dB到30dB变化时,4种算法的测向均方根误差,结果如图9所示。从图9中可以看出随着信噪比的增大,4种算法的测向均方根误差相应减小,并且本文算法和MUSIC算法的精度明显优于干涉仪测向法和文献[25]的算法。

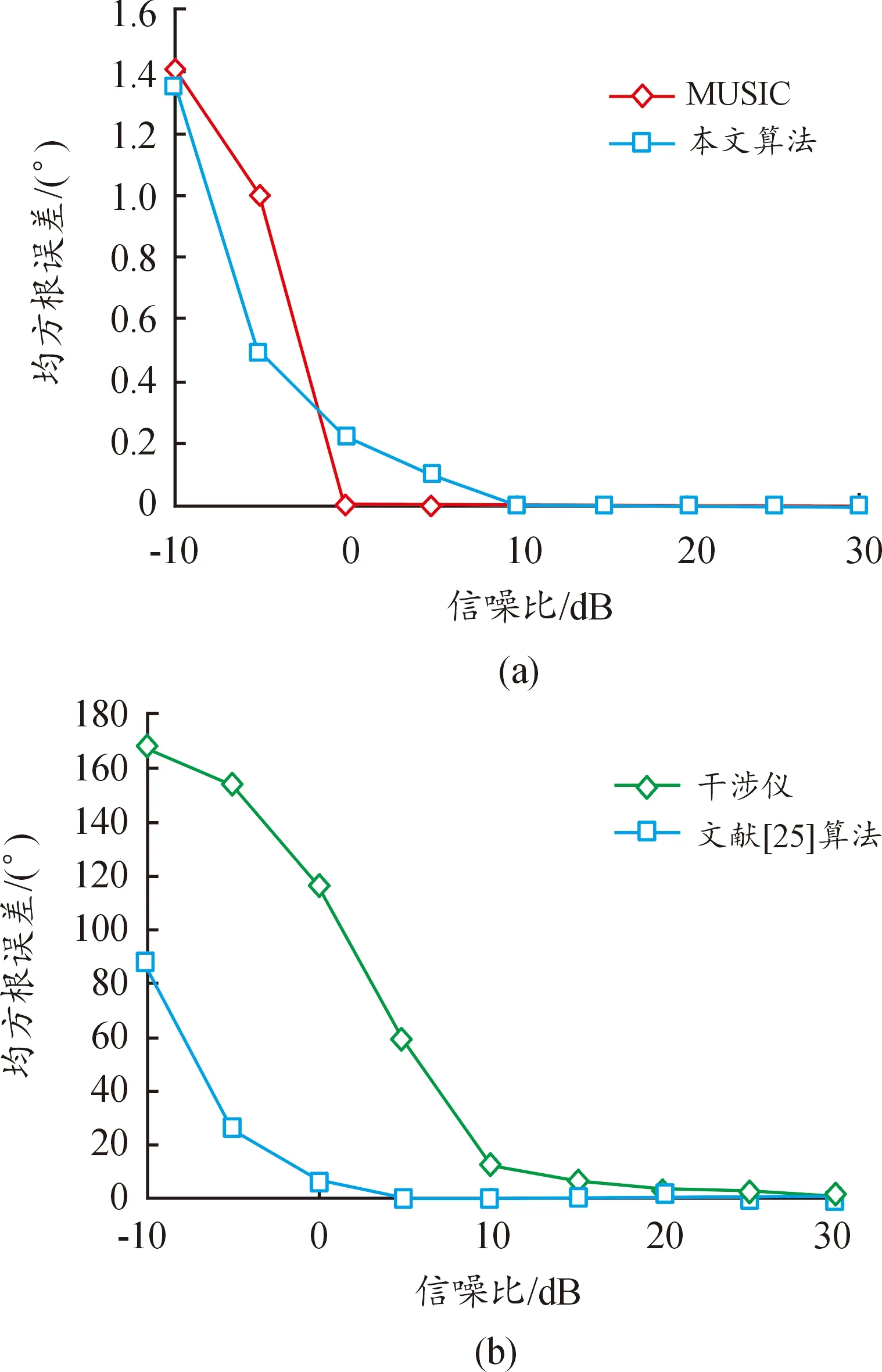
图9 均方根误差与信噪比的关系Fig.9 Relationship between RMSE and SNR

仿真2:4种算法的均方根误差与方位角变化关系

设俯仰角为40°,信噪比为5 dB,文章仿真了当方位角从0°～360°变化时,不同测向算法的均方根误差,结果如图10所示。

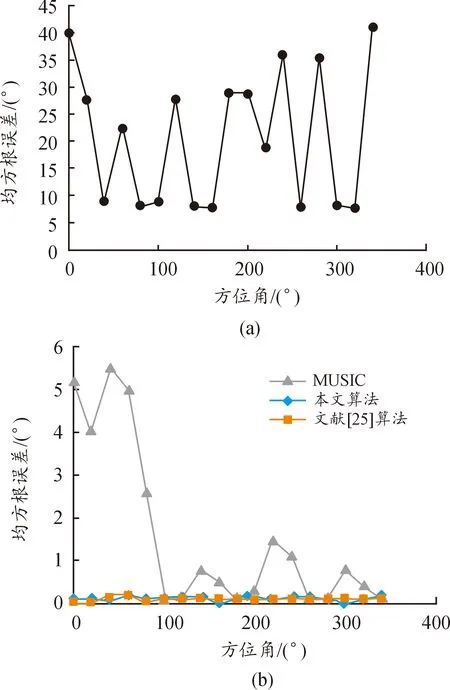
图10 均方根误差与方位角的关系Fig.10 Relationship between RMSE and azimuth

可以看出干涉仪测向法和文献[25]的均方根误差在360°范围内有明显起伏,并且数值较大,相反,本文算法和MUSIC算法的均方根误差在360°范围内变化较小,并且数值最小,说明了本文算法和MUSIC算法具有较强的鲁棒性和高精准度。

仿真3:4种算法的均方根误差与俯仰角变化关系

设方位角为40°,信噪比为5 dB,文章仿真了当俯仰角从5°～85°变化时,不同测向算法的均方根误差,结果如图11所示。

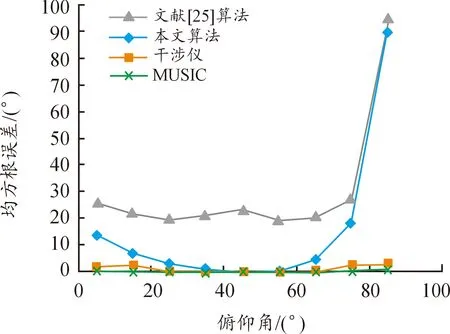
图11 均方根误差与俯仰角的关系Fig.11 Relationship between RMSE and pitch angle

可以看出当俯仰角位于45°附近时,均方根误差较小,干涉仪算法和文献[25]算法会随着俯仰角增大或减小,均方根误差都会增大。如图4所示,这是由于在干涉仪测向法中,当俯仰角取接近0°时,所测得的俯仰角误差会增大,当俯仰角取接近90°时,所测得的方位角误差会增大。并且由于整体均方根误差由俯仰角误差和方位角误差共同组成,从而导致随着俯仰角接近0°和90°极限值时,测向均方根误差都会增大。文献[25]算法并未考虑俯仰角接近极限值处时误差过大问题,所以导致产生与干涉仪算法类似的问题。MUSIC算法由于采用空间谱算法,不会有该问题产生。而文章在将干涉仪算法和MUSIC算法结合时,考虑到该问题,灵活选择搜索范围,从而避免了在极端角度值处误差过大的问题,具有更强的适应性。

4.2 测角耗时比较

仿真4:将本文算法的测向耗时与干涉仪测向算法、MUSIC测向算法及文献[25]算法进行比较。搜索步进为0.1°,信噪比为10 dB,在Matlab R2016a仿真环境中以tic-toc语句计算仿真时间,电脑配置如下:处理器为Intel(R)Core(TM)i7-9700CPU@3.00GHz;64位操作系统;16.0G内存。仿真结果如表1所示。

表1 仿真结果

从仿真结果可以看出,文章所提改进后的干涉仪联合MUSIC测向算法在同等环境中运行时间最短。文献[25]单纯将基于最小二乘法的干涉仪测向法和MUSIC测向算法简单结合,而文章首先对干涉仪测向算法进行改进,提高了干涉仪测向算法速度,而后将改进后的干涉仪测向算法与MUSIC 算法联合,使得整体运算速度更快。

由于仿真环境不同,文章对于文献[25]的实际试验所得仿真时间与文献[25]中得到的仿真时间不同,但是在同等仿真条件下,可以看出,文章所提算法运算时间相对于文献[25]明显减小。

文献[25]同样采用了干涉仪和MUSIC联合算法,该文献未考虑干涉仪测向法在不同俯仰角时测向误差的不同,而是在初步取得大致方位角后,单纯取正负10°范围做MUSIC搜索。然而当初步角度误差大于10°时,则不能保证MUSIC在正确范围内搜索,导致测向失效。文章在第三章分析了来波角度对测向的影响,在4.2节中针对误差分析结果调整MUSIC搜索范围,增强了联合算法的适用性。

综上所述,文章所提联合算法相对于干涉仪测向法提高了测向精度,相对于MUSIC测向法提高了运算速度,相对于简单的联合算法在方位角360°和俯仰角90°范围内具有更强的鲁棒性和适用性。