基于ADAMS的轴对称矢量喷管喷口精度分析

党鹏飞，王雨，杨铮鑫

(沈阳化工大学机械与动力工程学院，辽宁沈阳 110142)

0 前言

轴对称矢量喷管是飞机上的重要组成部件，通过调节尾喷偏转角度为飞机提供矢量推力，增强飞机的敏捷性、隐身性、超机动性和短距起降能力[1]。轴对称矢量喷管空间结构复杂[2]，在实际运行中，各种构件不可避免地存在误差，如杆件参数误差、运动副间隙、磨损及变形误差，约束与驱动也会产生随机误差，进而影响喷口精度[3-4]。因此在轴对称矢量喷管的设计和分析中，必须考虑构件参数误差对喷口精度的影响。王鑫、武建新[5]对轴对称矢量喷管进行动力学分析，获得动力学与运动学性能以及关键部件的受力情况；霍树林等[6]推导了A9喷口面积与作动筒位移量的函数表达式，通过ADAMS与MATLAB联合仿真，验证了公式的有效性；王贝等人[7]通过建立优化数学模型对轴对称矢量喷管构件参数进行多目标优化设计；王莉等人[8]分析了主要构件在高温高压下的变形对矢量角和喷口面积的影响；李晓明、伏宇[9]开发了轴对称矢量喷管机构参数优化选择及运动分析程序；李有德等[10]研究了误差对喷管喉道的影响；张哲等人[11]通过刚柔耦合动力学模型，分析了关键件柔性化对矢量喷管偏转效率的影响；李建榕、白伟[12]对影响偏转效率的参数进行实验，获得偏转效率、发动机工作特性变化等数据；樊开岗等[13]进行了数值模拟与实验，结果表明：偏转角在0°～ 20°之间，发动机推力损失较少。

影响喷口精度的各种因素具有随机性，在轴对称矢量喷管的生产、装配与运行过程中，这些误差客观存在，不可忽视。因此，本文作者借助ADAMS建立参数化模型，通过模拟仿真对制造误差、运动副间隙等几何误差源进行研究分析，得到各参数误差对喷口精度的影响程度。

1 轴对称矢量喷管介绍

1.1 轴对称矢量喷管结构

轴对称矢量喷管主要由A8收敛调节环、A9矢量控制环、机闸、拉杆、滚子、液压作动筒、收敛调节片、扩张调节片等零部件组成。图1(a)为作动筒周向分布：A9环上3个驱动作动筒周向间隔120°分布；A8环上6个驱动作动筒周向间隔60°分布；15组并联支链周向间隔24°分布。支链结构如图1(b)所示；约束类型见表1。

1.2 轴对称矢量喷管偏转原理

A9 喷口矢量偏转：3个作动筒输出不同的位移使 A9 环偏转，再通过拉杆带动扩张调节片在A8喉道的基础上收扩及偏转；通过控制扩张调节片不同位姿确定喷口面积与偏转角，改变气流方向，完成复杂运动[6]。

2 参数化模型

2.1 流程介绍

首先，在SolidWorks中建立轴对称矢量喷管装配体；其次，将该模型导入ADAMS中，添加约束与驱动，验证运动学模型有效性；再次，通过设计点建模在ADAMS中重新构建模型，并施加约束与驱动，验证误差模型的有效性。

2.2 建立模型

轴对称矢量喷管是复杂空间机构，虽然各支链结构相同，但无法通过复制、旋转的方式完成建模，这是因为复制的模型具有相同的参数化信息，而各支链的运动是不同的，必须对每一组支链单独建模。

首先，以机闸轴线为X轴，A1O所在的直线为Y轴，E2O所在的直线为Z轴，O为原点建立坐标系；通过运动学模型确定各零部件铰接点的位置，将其作为参数化模型设计点(即Point点)位置。其次，用连杆等建模命令将各点连接起来。最后，将部分无相对运动的零件使用布尔命令合并，如将扩张调节片中K1L1、D1L1与L1M1合并，三角拉杆简化为拉杆C1D1。

其中，机闸固定不动，视为大地。作动筒的建模以能够模拟液压缸伸缩为最低要求，没有必要创建复杂的模型，所以用圆柱来代替。A8环两端各有21个设计点，所以用21个连杆依次连接A8环两端的设计点，再通过布尔命令将21个连杆合并，使其质心位于机闸轴线上，替代原A8环。A9环两端各15个设计点，同样用连杆连接各设计点再合并，使其质心位于机闸轴线上，替代原A9环。滚子用圆柱代替，收敛调节片的轮廓用插值生成样条曲线代替。以机闸轴线为旋转轴，逆时针顺序，依次建立各组支链。各设计点命名如Ai、Bi、Ci、…、Mi(i=1，2，3，…，15)。材料的属性全部设置为钢(Steel)。建立的运动学模型如图2(a)所示，参数化模型如图2(b)所示。

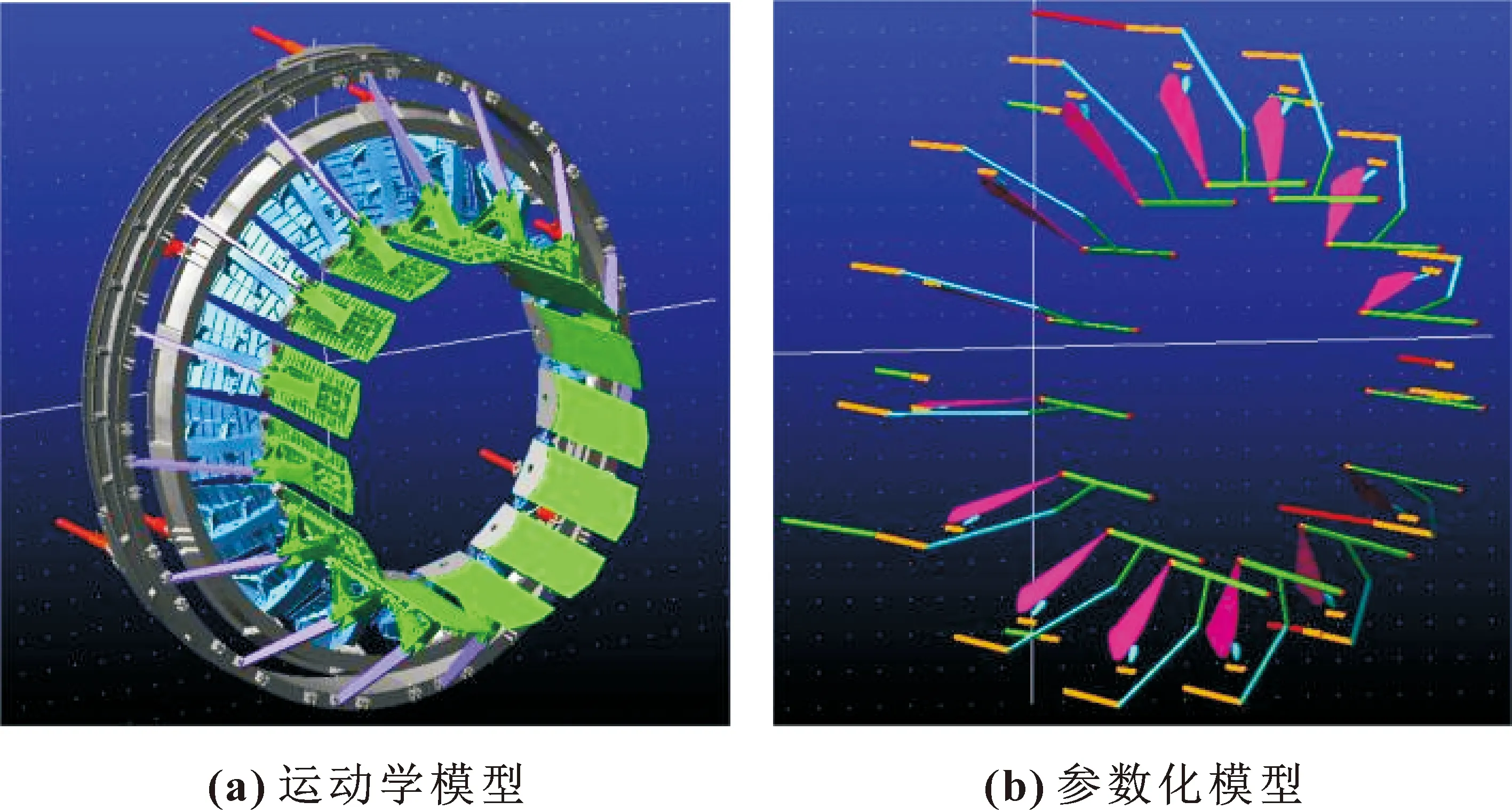
图2 轴对称矢量喷管模型Fig.2 Axial-symmetric vectoring exhaust nozzle models： (a)kinematic model；(b)parameterized model

2.3 验证模型

对轴对称矢量喷管运动学模型和参数化模型进行仿真，验证模型的有效性。测得A8环X方向的位移量如图3所示。A8环运动学模型与参数化模型在X方向上的最大偏离约为0.5 mm，误差约为3%，在可接受范围之内，参数化模型满足要求。

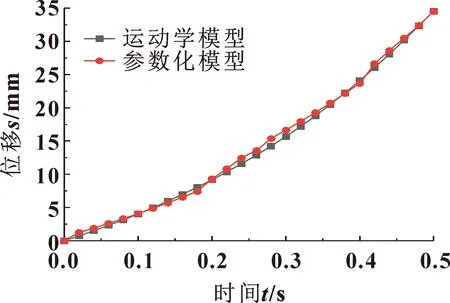
图3 仿真结果比较Fig.3 Comparison of simulation results

2.4 喷口精度参数

轴对称矢量喷管主要由偏转角、方位角、喷口面积参数来确定发动机状态，使发动机工作范围稳定。轴对称矢量喷管最大可实现偏转角20°、方位角360°的收扩-偏转运动。由于实际模型中各扩张调节片之间有密封装置约束，防止扩张调节片之间的干涉与分离，所以文中在参数化模型中取喷口圆度较大的工况为研究对象，即偏转角为8.87°、方位角为42°的工况。

如图4(a)所示，2条绿线构成的夹角就是偏转角；图4(b)中，黄色的圆为仿真初始时喷口面积，红色的圆为仿真结束时喷口扩大的面积，白色的线为各点Mi轨迹，红点为仿真终止时喷口形心。

图4 仿真终止模型Fig.4 Simulation termination model：(a)deflection angle； (b)nozzle area

A9喷口形心可以看作由15个点Mi构成的点集的中心，公式定义为

(1)

同理，可求得A8喉道形心J。

A9喷口的形心M与A8 喉道的形心J的连线与机闸轴线的夹角为偏转角α，如图5(a)所示，公式定义为式(2)；形心M在YOZ平面上的投影与Z轴负方向的夹角为方位角β，逆时针为正方向，如图5(b)所示，公式定义为式(3)。

(2)

(3)

喷口面积可看作一系列离散点Mi在YOZ平面上的投影首尾相连形成的封闭多边形的面积，由任意多边形公式(式(4))可求出喷口面积：

(4)

其中：Zn+1=Z1；Yn+1=Y1。

2.5 建立测量函数

使用Function Builder编辑器，依次建立位移测量函数DX、DY、DZ，可求出点J与点M坐标的绝对值。再通过数学函数编辑输入式(2)—(4)分别求得喷口偏转角、方位角与喷口面积。

3 单一设计变量灵敏度分析

3.1 灵敏度介绍

由于轴对称矢量喷管的复杂性，设计点众多，各设计点的不同参数变化均会对喷口精度产生影响，因此需找出对喷口精度影响较大的关键设计点的变量。灵敏度反映了喷口精度对各构件设计变量的依赖关系，求得灵敏度，可以针对性地对设计变量进行调整。

灵敏度函数表达式：

(5)

式中：F(xi)为目标值变化的差值；Δxi为设计参数变化量。

3.2 灵敏度分析

使用设计研究功能，逐一分析各设计点的X、Y、Z对喷口精度影响的灵敏度，共165个设计点，495个设计变量。由于同一零部件上有15个不同周向位置的设计点，受篇幅限制，筛选出不同零部件中对喷口精度影响最大的设计变量，按灵敏度的绝对值由高到低排列，并在μ=±0.1 mm情况下，计算各设计变量最大误差，偏转角、方位角、喷口面积结果如表2—4所示。

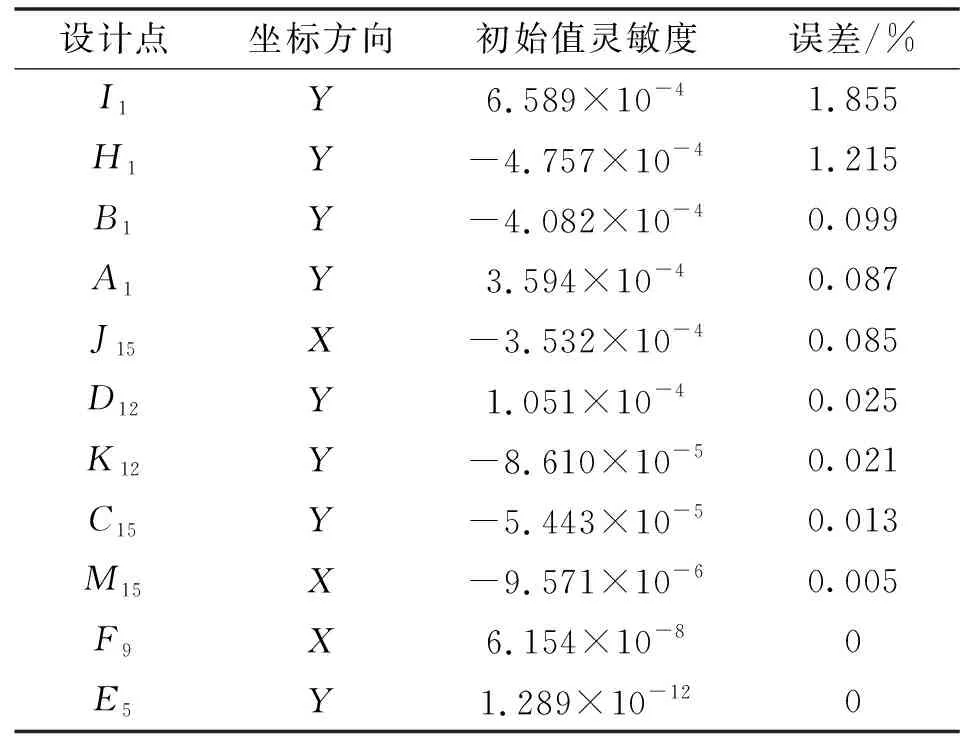
表2 偏转角分析结果Tab.2 Analysis results of deflection angle

由表2可知：灵敏度最大的是I1的Y方向，说明在仿真中，滚子I1的Y坐标改变会对偏转角产生最大的影响，误差为1.855%；其次是H1的Y方向，说明收敛调节片的点H1的Y坐标改变会对偏转角产生较大影响，误差为1.215%；同理可分析表3、4。综合所有的设计研究结果可知：滚子所在的设计点(点Ii)灵敏度最大，其次是收敛调节片设计点(点Hi)。这是因为滚子与收敛调节片为线接触高副机构，轮廓加工精度高、安装要求高且容易磨损，所以在设计、实验及实际运行中应重点关注滚子与收敛调节片的状态。

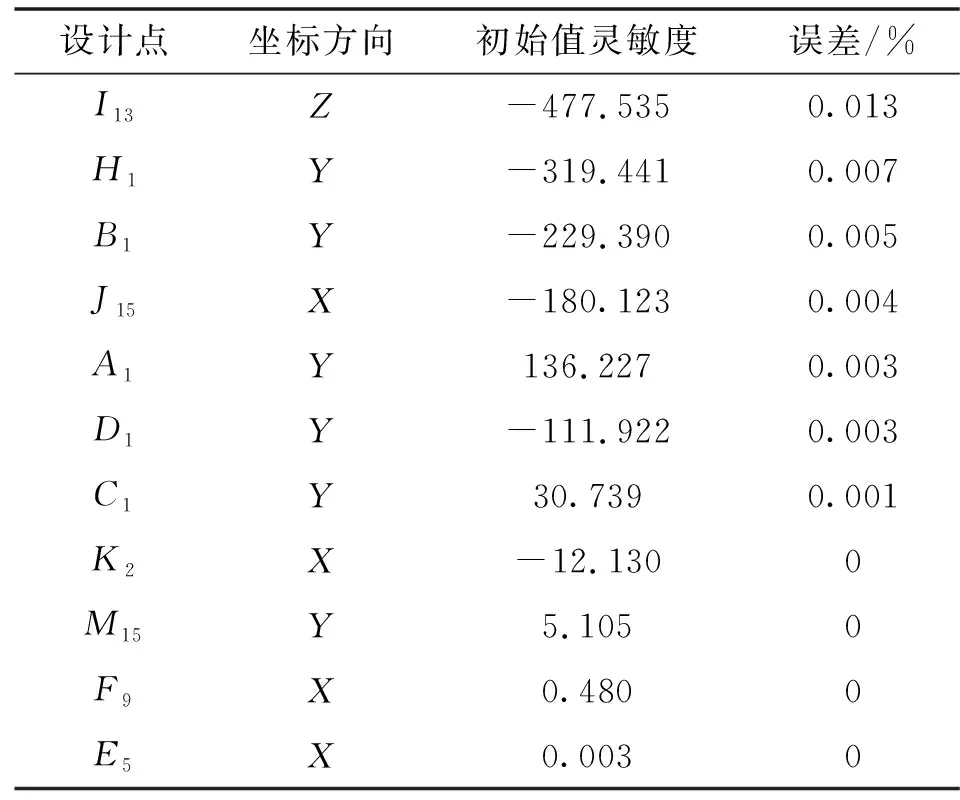
表4 喷口面积分析结果Tab.4 Analysis results of nozzle area

4 蒙特卡洛分析

实际运行中，各种误差随机存在，为模拟实际运行状态，需从概率分布的角度出发，研究各种随机误差对喷口精度的影响程度。蒙特卡洛法是一种通过建立概率分布模型，对随机实验结果进行概率统计，获取期望发生频率的方法。

首先，在ADAMS/Insight中，将偏转角、方位角、喷口面积3个测量函数设为响应值，将495个设计变量设为影响因素；其次，令495个影响因素在-0.1 mm<μ<0.1 mm内生成服从正态分布的500个样本数据，为减轻计算机工作量，采用蒙特卡洛法随机抽取500次样本数据进行仿真，得到随机误差对响应值的影响程度。

然后，分析同类零部件随机误差对响应值的影响程度；如滚子的随机误差分析，仅抽取滚子所在15个设计点的X、Y、Z方向共45个影响因素的样本数据，其他构件默认为理想构件，采用蒙特卡洛法仿真1 000次，对偏转角影响结果如表5所示。按同样步骤分析得零部件随机误差对方位角的影响(表6)以及其对喷口面积的影响(表7)。

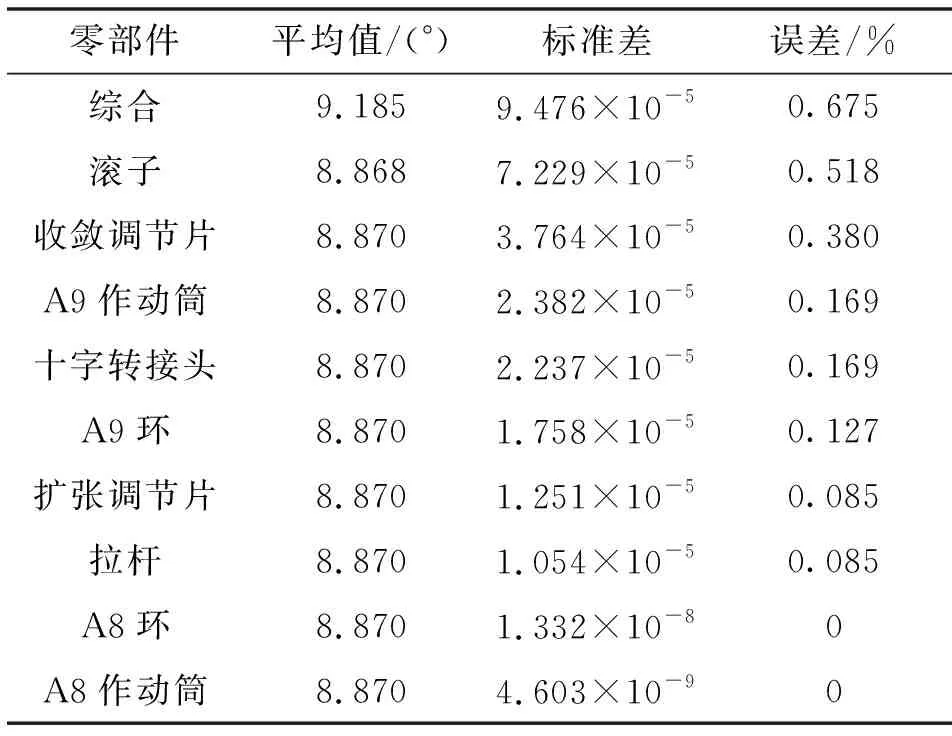
表5 偏转角影响结果Tab.5 Influence result of deflection angle result

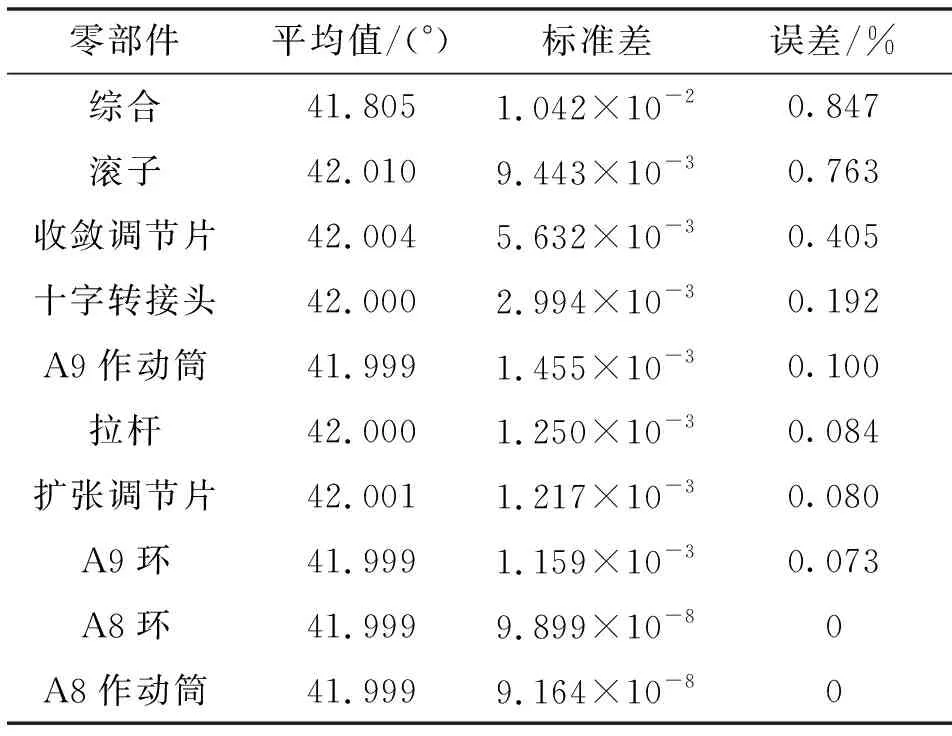
表6 方位角影响结果Tab.6 Influence result of azimuth angle

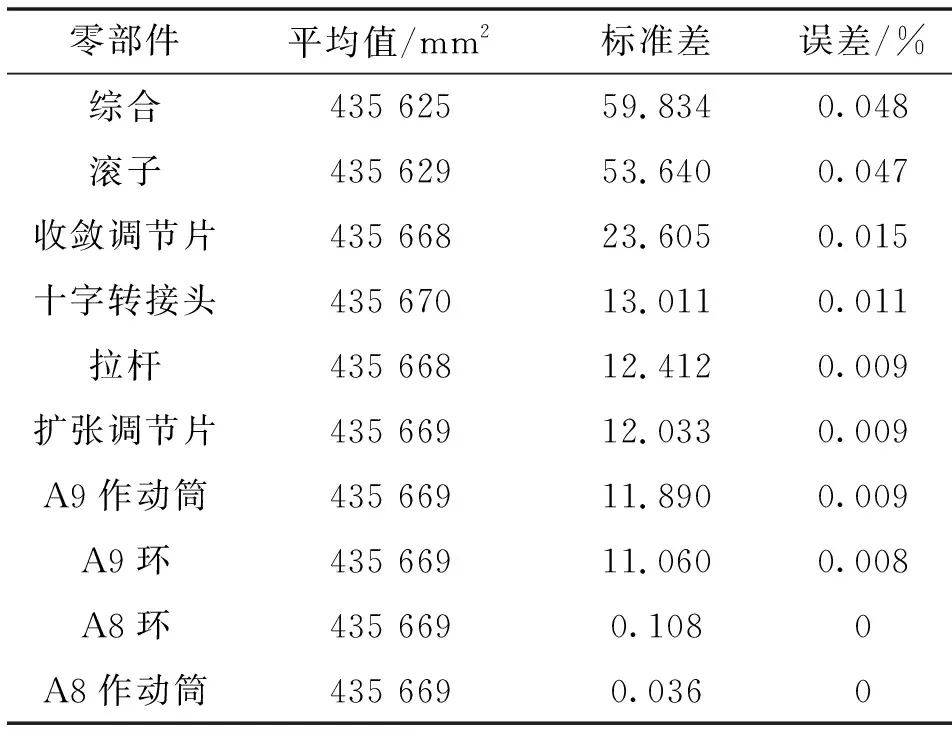
表7 喷口面积影响结果Tab.7 Influence result of nozzle area

由表5可看出：考虑所有设计变量随机误差对偏转角的影响最大，误差为0.675%。仅考虑滚子随机误差对偏转角影响较大，误差为0.518%；其次是仅考虑收敛调节片随机误差，误差为0.38%。同理，分析表6、7可知：考虑所有设计变量的随机误差对喷口精度的影响最大；其次，是仅考虑滚子随机误差；再次，是仅考虑收敛调节片随机误差。

5 结论

(1)使用ADAMS中设计研究功能对单一设计变量进行灵敏度分析，得出滚子所在点Ii对喷口精度影响最大；其次，是收敛调节片所在点Hi对喷口精度影响较大。

(2)借助ADAMS/Insight里的蒙特卡洛方法分析，结果表明：在考虑随机误差-0.1 mm<μ<0.1 mm的情况下，偏转角误差为0.675%、方位角为0.847%、喷口面积为0.048%，整体变化较小，可以保证喷口精度。并从仅考虑同类零部件随机误差的实验中得出：影响喷口精度的主要是滚子，其次是收敛调节片。因此在实验设计与实际飞行中应重点关注滚子与收敛调节片的状态。