基于期望轨迹修正的机械臂无传感器柔顺控制
2023-12-04朱敬花邵珠枫
朱敬花,邵珠枫
(1.九州职业技术学院机电与汽车工程系,江苏徐州 221000;2.中国矿业大学信息与控制工程学院,江苏徐州 221000)
0 前言
人机交互一般是指机器人/机械臂与自然人之间的交互,接触式人机交互是最普遍、最广泛的人机交互方式,在装配机器人、手术机器人、护理机器人中得到了广泛应用[1]。由于接触式交互机器人和自然人处在共同的工作空间,交互安全是首要考虑的问题,其次还要考虑交互的柔顺性、自然性和平滑性。因此,研究人机间的柔顺接触交互问题,对于保证交互安全、提高机器人服务质量具有重要意义。
机械臂接触式交互的柔顺性是指机械臂与外界环境接触时产生顺从运动的能力,根据控制方式的不同,机械臂柔顺控制包括被动柔顺控制和主动柔顺控制2类[2]。被动柔顺控制是指以弹簧、阻尼等吸能或储能元件作为辅助元件,使机械臂对环境的接触力产生被动的柔顺。被动柔顺控制这种借助外部元件的实现方式,无法满足机械臂的高精度、高柔性接触要求[3],因此主动柔顺控制应需而生。主动柔顺控制是指根据反馈的接触力信息,通过主动控制接触力大小的方式,实现机械臂与环境交互的柔顺性。主动柔顺控制包括力/位控制和阻抗控制2类[4]。力/位混合控制的核心思想是将任务空间分解为相互独立的位置控制子空间和力控制子空间,并各自进行独立控制的方式[5]。力/位混合控制在机械臂和环境参数已知的情况下可以取得较好的控制效果,但是在参数未知情况下难以取得预期效果。阻抗控制将机械臂与环境接触过程建模为质量-阻尼-弹簧系统,并针对力和位移之间的关系进行动态控制[6]。根据实现方式的不同,阻抗控制分为力阻抗控制和位置阻抗控制,在环境参数未知的前提下,位置阻抗控制表现出更强的鲁棒性和环境适应性。文献[7]针对空间机械臂加注时的插孔控制问题,设计了基于阻抗控制的柔顺控制方法,通过仿真验证了该方法的有效性。文献[8]研究了漂浮空间机器人抓捕不配合卫星过程的柔顺控制问题,设计了一种旋转型串联弹性执行器,经仿真验证了该方法在卫星抓捕过程中的有效性。文献[9]针对重载液压机械臂的柔顺控制问题,提出了基于遗传神经网络的位置/力同环控制算法,用于高功率动态机械臂的柔度控制。
柔顺控制需要已知机械臂的动力学参数并感知末端接触力,但是存在以下问题:(1)动力学参数一般通过人为设定或者试验得到,但是当前辨识方法存在损失函数鞍点多、辨识误差大等问题;(2)末端接触力需要力传感器进行测量,这种方式增加了系统复杂度,也限制了柔顺控制的推广使用。
针对上述问题,本文作者研究机械臂系统动力学参数的递归辨识方法和柔顺控制方法。首先,针对传统辨识方法损失函数鞍点多、易陷入局部最优、计算量大的问题,提出机械臂由外向内递归的参数辨识方法;其次,针对机械臂柔顺控制问题,设计基于非奇异终端滑模控制的位置阻抗控制器;最后,通过实验验证上述方法的有效性和优越性。
1 机械臂动力学模型及参数辨识
1.1 包含未知参数的动力学模型
对于具有N个关节的机械臂系统,考虑系统中的未知扰动和摩擦力矩,得到机械臂系统动力学方程[10]为
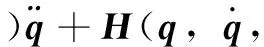
(1)
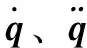
摩擦的类型包括滑动摩擦、滚动摩擦和静摩擦,人机交互运动过程中,机械臂摩擦力主要表现为滑动摩擦,则:
(2)
式中:ν=diag(ν1,ν2,…,νN)为关节的滑动摩擦因数。
将动力学方程中的未知参数全部归纳到矩阵ϑ中,为
(3)
式中:ϑi为关节i的未知参数矩阵;mi为连杆i的质量;Ii为连杆i的转动惯量;νi为关节i的滑动摩擦因数。
1.2 基于递归的参数降维辨识方法
(4)
上述参数辨识方法的目标函数为minL,但是这种辨识方法存在以下问题:(1)未知参数共有3N个,全部耦合在一起进行辨识,极大地增加了计算量和计算复杂度;(2)损失函数的损失面函数存在大量鞍点(即局部极值点),辨识过程中容易陷入局部最优而降低参数辨识精度。
为了解决上述问题,作者采用递归的方式由外而内地辨识连杆动力学参数,实现了参数降维,降低了算法复杂度,同时解决了损失面函数的鞍点问题。对连杆i进行力分析和力矩分析,如图1所示。
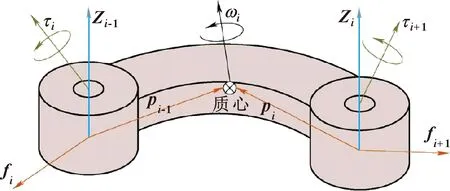
图1 连杆力/力矩分析Fig.1 Force/moment analysis of connecting rod
图1中:Zi-1和Zi分别为关节i-1和关节i的Z坐标轴;fi为连杆i受到的合力;τi为连杆i的驱动力矩;ωi为连杆i质心的转动角速度;pi为关节相较于质心的力臂。连杆i质心位置受到的力Fi和力矩Ti为
(5)
式中:vci连杆i质心的线速度矢量;Δt为采样间隔。
基于牛顿-欧拉法得到连杆i的驱动力矩τi为
(6)
使用递归的方法由外而内依次辨识机械臂的动力学参数,具体步骤为:
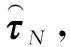
(2)由外向内递归,依次辨识出连杆N、N-1、…、1的动力学参数。
将文中基于递归的参数辨识法与传统的辨识方法相比,可以看出此辨识方法具有以下优势:
(1)式(4)给出的传统辨识法中,共有3N个参数同时辨识;此方法每次辨识3个参数,通过N次辨识完毕,实现了辨识参数的单次降维,极大地降低了计算过程的复杂程度;
(2)从损失函数的角度讲,传统辨识方法损失函数中包含3N个平方项的和;此辨识方法的损失函数中只包含3个平方项的和,这意味着传统损失面函数的鞍点(极值点)必然远远多于此辨识方法。因此,此方法的辨识精度从理论上高于传统辨识方法。
2 机械臂柔顺控制方法
此节设计了非奇异终端滑模阻抗控制器,实现对机械臂的柔顺控制。其核心思想是:将机械臂末端的接触力转化为轨迹偏差,通过对期望轨迹进行修正,实现全关节空间的柔顺控制。
2.1 基于位置阻抗控制的期望轨迹修正方法
阻抗控制将机械臂末端与环境之间的接触模型等效为质量-阻尼-弹性模型,如图2所示。其中:M为接触模型的质量矩阵;B为阻尼矩阵;K为弹性矩阵;Fe为环境接触力。
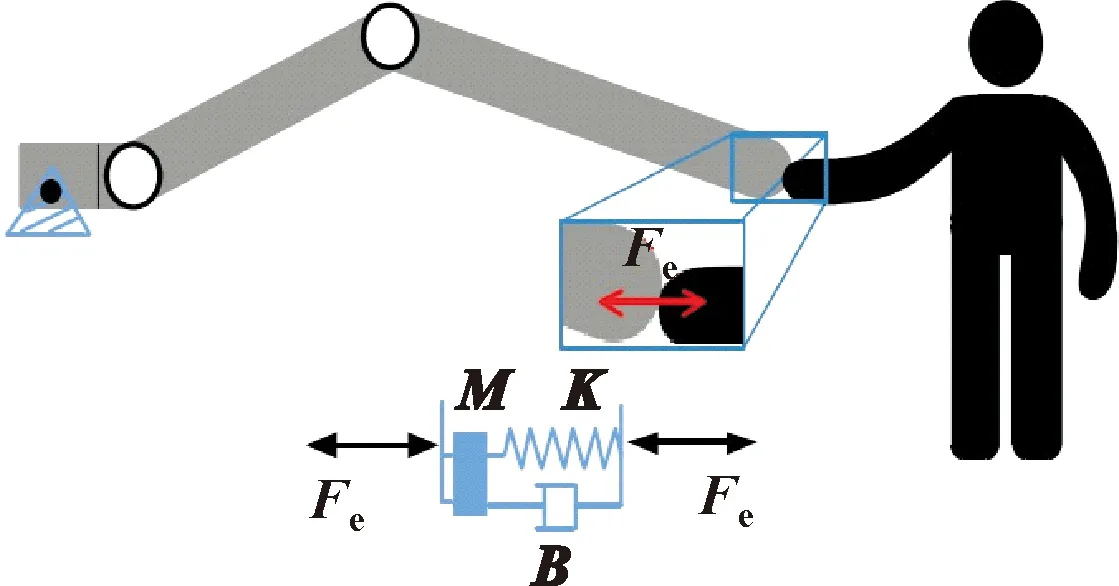
图2 阻抗模型Fig.2 Impedance model
对机械臂的关节轨迹进行跟踪控制,实现关节位置的二阶阻抗模型[11]为
(7)
式中:qex为期望的关节角位置;q为实际的关节角位置。
稳态时,机械臂的接触力为
K(qex-q)=Fe
(8)
基于雅可比矩阵,可以将机械臂接触力Fe转化为关节驱动力τe:
τe=JTFe
(9)
式中:J为雅可比矩阵。
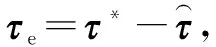
(10)
式中:qxz为修正的期望关节角轨迹。
分析式(10)可知:基于机械臂动力学模型,可以将接触力转化为关节角轨迹的修正值,通过对期望轨迹进行修正,实现机械臂末端的柔顺控制。综合上述分析,得到阻抗控制框架如图3所示。

图3 阻抗控制框架Fig.3 Framework of impedance control
图3给定的阻抗控制方法,通过将接触力转化为期望轨迹修正量,实现了机械臂的柔顺控制。但是其中的角位置控制器尚未设计,在下一小节中实现。
2.2 考虑参数不确定性的角位置控制器设计
在设计角位置控制器时,需要考虑以下2个方面:(1)必须考虑动力学参数不确定性引起的控制误差,并对这一控制误差进行补偿;(2)机械臂控制具有较高的实时性要求。针对上述2个方面,角位置控制器设计如下:(1)使用RBF神经网络对参数不确定性进行补偿;(2)考虑到非奇异终端滑模控制具有快速收敛、稳态精度高的优点,基于非奇异终端滑模控制设计机械臂控制器。
定义角位置跟踪误差为e=qxz-q,设计非奇异终端滑模面s为
(11)
式中:s=(s1,s2,…,sN)T为各关节控制器滑模面;λ=diag(λ1,λ2,…λN)为滑模面斜率矩阵;m和k为人为设定的正奇数,要求m∈(k,2k)。
将机械臂接触力转化的驱动力τe考虑到动力学方程中,则式(1)可以写为
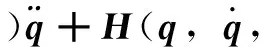
(12)
对非奇异终端滑模面函数s求导,并将式(12)代入,得:
(13)
参考文献[12]设计一种具有快速收敛能力的指数趋近律:
(14)
式中:a>0、b>0为人为设定参数。选取较大的a值,可以使系统状态的趋近速度远大于等速趋近过程,从而提高机械臂轨迹的跟踪速度。
将式(13)代入到式(14)中,并使用RBF神经网络对未知扰动τd进行估计,得到控制律τ为
(15)
式中:τ为机械臂控制律;τ1为逆动力学的解算力矩;τ2为趋近过程控制力矩;τ3为基于RBF神经网络的补偿力矩;θ为网络权值矩阵;φ(χ)为激活函数,χ为神经网络输入参数。
(16)
式中:Γθ为正定实数矩阵。
2.3 柔顺控制框架及稳定性分析
基于上述位置阻抗控制器和角位置控制器的设计原理,得到机械臂柔顺控制框架如图4所示。
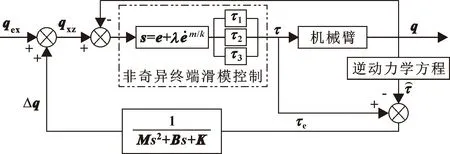
图4 机械臂柔顺控制框架Fig.4 Framework of manipulator compliance control
使用Lyapunov理论[13]对机械臂控制系统的稳定性进行分析,能量函数设计为
(17)
对能量函数求导,得:
(18)
分别代入τ1、τ2、τ3,得
(19)
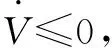
3 实验验证与分析
此节从2个方面对柔顺控制方法进行验证:(1)对动力学参数进行辨识和精度验证;(2)对柔顺控制的位置控制和接触力控制精度进行验证。
3.1 动力学参数辨识与精度验证
搭建的机械臂实验平台包括工控机、电气控制柜和机械臂本体,其中机械臂本体固定在支架上,如图5所示。

图5 机械臂实验平台Fig.5 Experimental platform of manipulator:(a)experimental system;(b)manipulator body
机械臂本体由肩关节1、肩关节2、大臂、肘关节和小臂组成。不同关节角轨迹对辨识参数的激发效果是不同的,文中使用对干扰不敏感、速度和加速度平滑性极好的Fourier级数作为关节角轨迹:
(20)

对于关节i,其激励轨迹的待定系数具有2D+1个,为了充分激发出关节动力学参数、提高参数辨识精度,最优激励轨迹的确定使用文献[14]中的确定方法。而后分别使用传统辨识方法和递归辨识方法对动力学参数进行辨识,结果如表1所示。
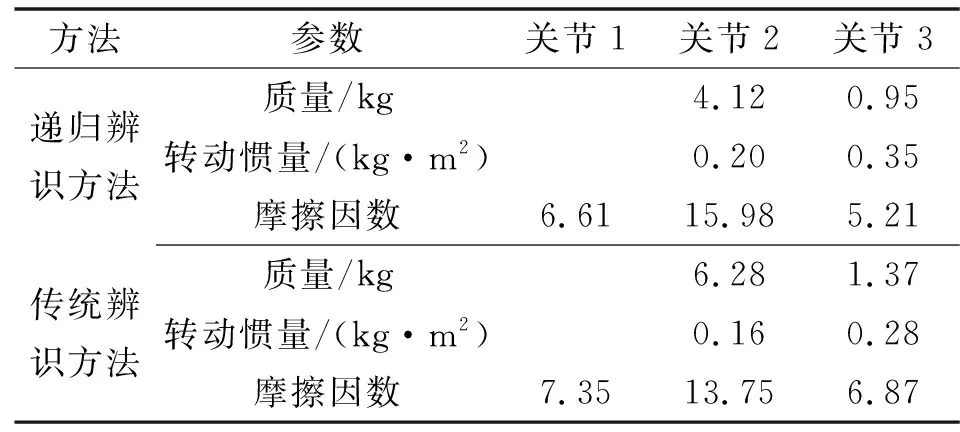
表1 动力学参数辨识结果Tab.1 Identification results of dynamic parameters
基于第1.2节的参数递归辨识方法,得到参数辨识结果如表1所示。
由表1可知:传统方法和递归方法得到的辨识结果有一定差别。由于动力学参数真值未知,无法直接比较2种辨识方法的优劣。将参数辨识结果代入式(1)中得到辨识力矩,再与真实力矩比较,以关节2的辨识结果为例,结果如图6所示。
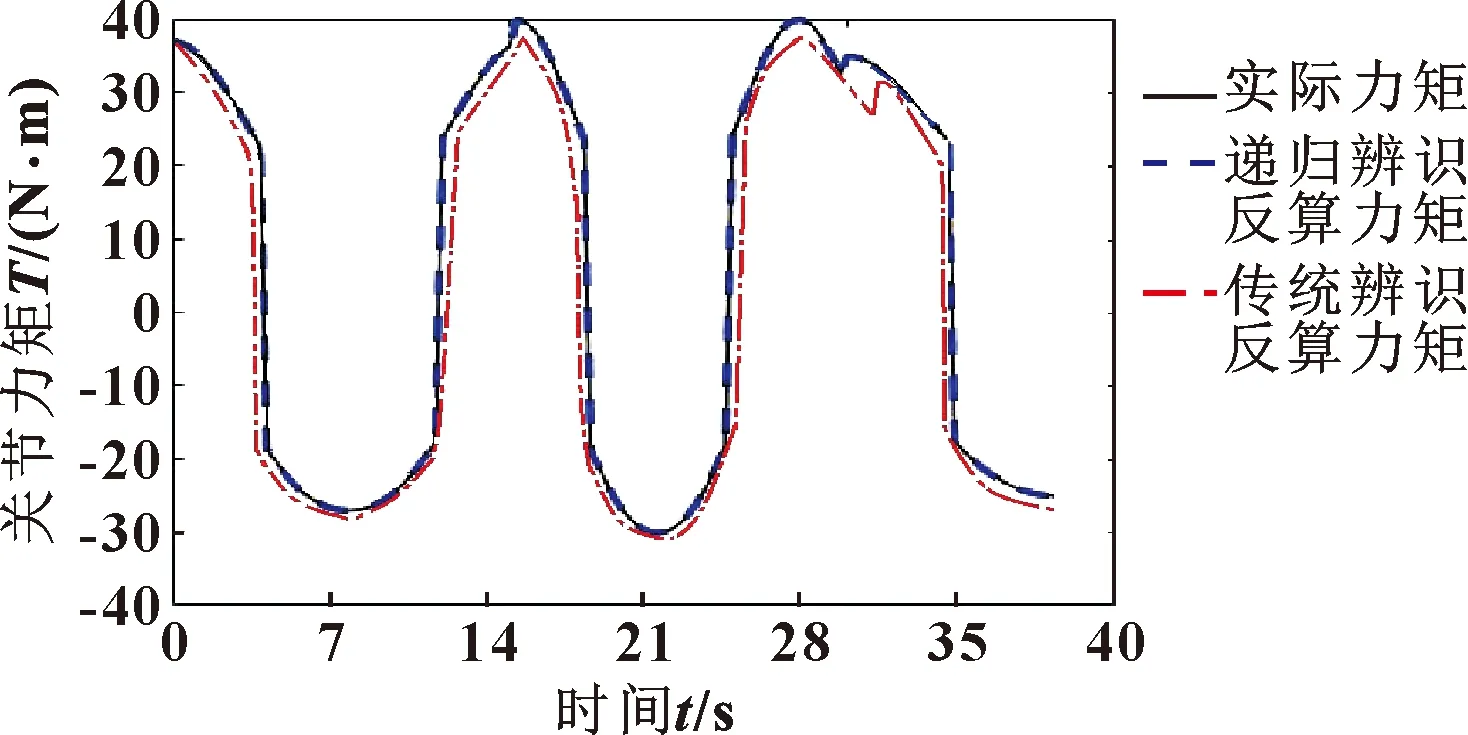
图6 关节2的力矩反算结果Fig.6 Torque inverse calculation result of joint 2
统计2种方法反算力矩的累计绝对误差,传统辨识方法反算力矩的累计绝对误差为9.35 N·m,递归辨识方法反算力矩的累计绝对误差为1.05 N·m。结合图6可知:传统辨识方法反算力矩与真实力矩的误差明显大于递归辨识方法反算力矩的误差。这是因为传统辨识方法同步辨识所有的参数,损失面函数中存在大量的鞍点位置,在辨识过程极易陷入局部最优位置;而递归辨识方法由外向内逐步递归,一步只辨识一个机械臂的未知参数,其损失面函数中鞍点极少,因此递归辨识方法的参数精度远远高于传统辨识方法。
3.2 柔顺控制效果验证
以机械臂定点打磨平面形的铝合金计算机外壳为例,铝合金计算机外壳如图7所示。
将期望接触力设置为20 N,阻抗参数设计为M=[20,20,20]T,B=[200,200,200]T,K=[150,150,150]T。根据任务需要,机械臂3个关节的期望关节角分别为0°、24°、41°。在机械臂末端加装力传感器,测量末端接触力,从而验证柔顺控制效果。
图8给出了关节1-3的期望轨迹、修正的期望轨迹和实际跟踪轨迹,可知:实际轨迹能够较为精确地跟踪修正的期望轨迹,说明非奇异终端滑模控制器能够快速、精确地跟踪期望轨迹。
为了验证基于位置阻抗控制对接触力的控制效果,同时使用文中方法与文献[15]的神经网络阻抗控制方法对铝合金计算机外壳进行打磨,2种方法的接触力控制效果如图9所示。
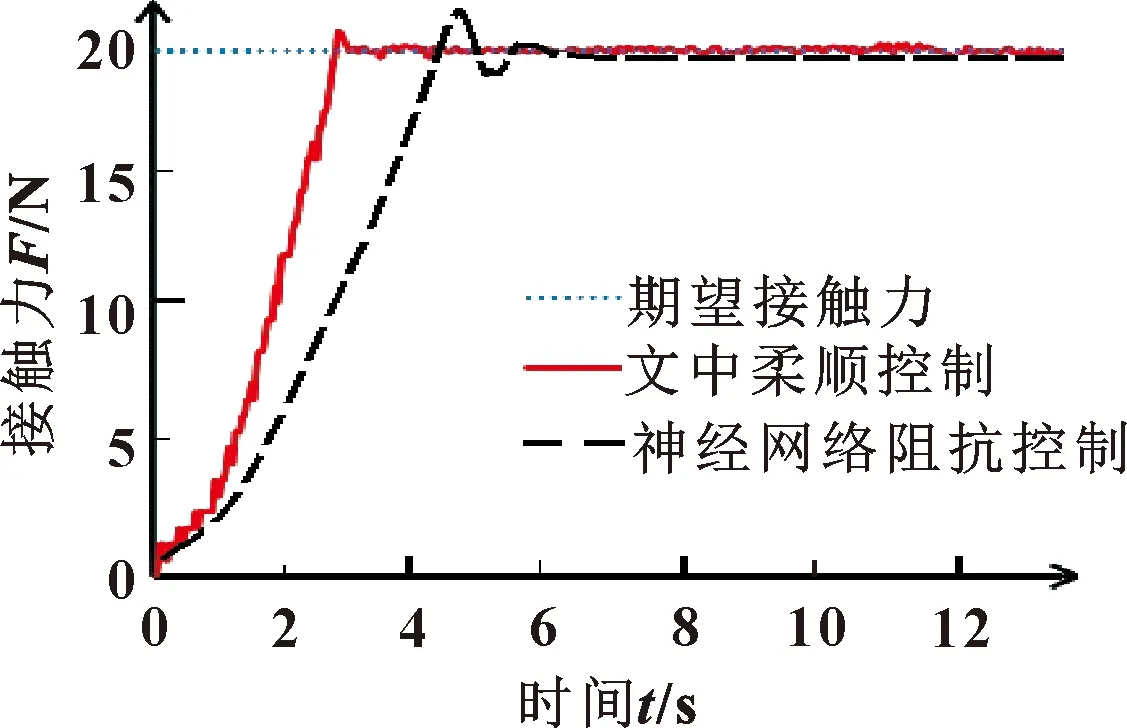
图9 接触力控制效果Fig.9 Control effect of contact force
经计算,在文中位置阻抗控制下,接触力误差最终在±0.4 N范围内波动;在神经网络阻抗控制作用下,接触力误差最终在[-1.8,-0.5]N内波动。另外,在文中位置阻抗控制作用下,接触力在2.8 s达到设定值;而在神经网络阻抗控制作用下,接触力在5.4 s达到设置值。结合图9的控制效果可知:文中位置阻抗控制方法可以快速、准确地跟踪设定接触力。这是因为:(1)使用递归参数辨识方法有效提高了参数的辨识精度,进而提高了控制精度;(2)在角位置跟踪控制中,利用快速收敛、稳态精度高的非奇异终端滑模控制器进行跟踪,实现了角位置的快速、精确控制。
实验结果表明:基于期望轨迹修正的位置阻抗控制能够实现机械臂与环境的自然、柔顺交互,能够快速、准确跟踪设定的接触力。
4 结论
文中研究了机械臂系统的动力学参数辨识与主动柔顺控制问题,首先针对传统辨识方法存在的鞍点多、易陷入局部最优、计算复杂等问题,提出了机械臂参数由外而内的递归辨识方法。然后针对机械臂与环境交互的柔顺控制问题,设计了基于非奇异终端滑模控制的位置阻抗控制器。
经实验验证得出以下结论:(1)基于传统辨识方法的反算力矩累计绝对误差为9.35 N·m,基于递归辨识方法的反算力矩累计绝对误差为1.05 N·m,说明参数递归辨识精度远高于传统辨识方法;(2)文中位置阻抗控制作用下,接触力在2.8 s达到设定值,误差波动范围为±0.4 N,与神经网络阻抗控制比具有更高的控制精度和更快的跟踪速度。
