基于拉曼光谱结合角度转换的安息香结晶热力学研究
2023-12-03马鑫刘安民姚志湘
马鑫 刘安民 姚志湘

摘 要:采用拉曼光谱结合角度转换算法,建立安息香质量浓度与角度值的曲线方程,在热力学温度为273.15~343.15 K范围内,通过静置法与直接目测法观察安息香在95%乙醇中的饱和温度,测得的光谱数据经角度转换得到一系列角度值,由关联方程直接得出饱和溶解度与过饱和溶解度,用修正的Apelblat方程对溶解度数据进行关联,绘制介稳区,并通过van't Hoff 模型以及Gibbs-Heimholtz方程计算相关溶解热力学数据。结果表明:建立的模型方程相关系数r为0.995 9,验证模型相对误差在-4.29%~3.37%。Apelblat方程拟合的溶解度曲线相关系数r分别为0.999 1及0.999 0,安息香在95%乙醇溶液中的溶解度与过饱和溶解度随着温度的升高而增大,而介稳区宽度随着温度的升高而减小。计算得到安息香晶体溶解过程中的溶解焓为47.32 kJ/mol,结晶焓为-47.32 kJ/mol,溶解熵为173.63 J/(mol·K),吉布斯自由能为-6.18 kJ/mol,其溶解过程是一个随着温度升高而自发进行的吸热过程。与目前常用的重量法求溶解度相比,该方法簡便快捷,通过采集不同温度下的安息香拉曼光谱,就能直接计算出安息香的浓度,可以用于多种体系的热力学分析研究。
关键词:安息香;结晶热力学;溶解度;过饱和溶解度;介稳区
中图分类号:TQ651.2;R284.1 DOI:10.16375/j.cnki.cn45-1395/t.2023.04.017
0 引言
在化工行业中,结晶是一种重要的晶态化学品分离纯化技术[1],而其中的结晶热力学研究,是对结晶设备和结晶工艺进行选择和设计的基础。目前国内外对于安息香的研究,主要在其药理作用及合成等方面[2],未见对安息香结晶热力学性质以及在95%乙醇溶液中的溶解度数据研究报道。
郭盛争等[3]利用激光动态法与称重法计算了莱鲍迪苷A在不同混合溶剂体系中的溶解度;张红蕾等[4]采用静态法和称重法计算得到了在298.15~318.15 K(K为热力学温度)范围内的番茄红素晶体在不同比例正己烷-丙酮混合溶剂中的溶解度;Liu等[5]在288.15~328.15 K范围内,采用重量法得到了4-硝基吡唑在不同有机溶剂中的溶解度。不难发现,现有测定溶解度的方法通常是先采用静态法[6]、动态激光法[7]、重量法[8]观察,确定饱和温度与过饱和温度,再通过称重法计算溶解度,其中称重法计算溶解度的过程操作比较繁琐,耗费时间较长,不能兼具高效性与准确性。目前较为常用的溶解度数据关联模型有Wison方程[9]、λh方程[10]、NRTL方程[11]及Apelblat方程[12-13]等,其中Apelblat方程是最常用的简化方程,计算方便,准确度高,适用体系更广泛。
基于此,本文采用拉曼光谱结合角度转换算法[14-15],通过建立安息香质量浓度与夹角值θ的关联方程,结合静置法与直接目测法,在273.15~343.15 K范围内,直接计算得到安息香在95%乙醇中的饱和溶解度与过饱和溶解度,并对其介稳区、溶解熵、溶解焓以及吉布斯自由能等溶解热力学数据进行研究计算。
1 实验仪器与药品
1.1 实验仪器
拉曼光谱仪(ExR610,西派特(北京)有限公司)、电子分析天平(CP214型,奥豪斯仪器(常州)有限公司)、低温恒温反应浴(DFY-5L/10、巩义市予华仪器有限责任公司)、程控搅拌器(MYP12-2,上海梅颖浦仪器仪表制造有限公司)。
1.2 实验药品
无水乙醇(AR,成都市科隆化学品有限公司)、安息香(AR,天津市光复精细化工研究所)。
2 实验方法
2.1 安息香-95%乙醇结晶体系拉曼光谱快速分析模型的建立
2.1.1 安息香建模样本的制备
精确称取5.002 9 g分析纯安息香样品,加入95%乙醇定容到50 mL,搅拌溶解,制成50 mL质量浓度为100.06 g/L的安息香-95%乙醇标准溶液。分别用移液管量取定量的95%乙醇并定容到10 mL,震荡摇匀,依次配制质量浓度为10.01、20.01、30.02、40.02、50.03、60.04、70.04、80.05、90.06、100.06 g/L的待测样本溶液,命名为S1—S10。
2.1.2 样品拉曼光谱采集条件
将S1—S10样本溶液分别放进测量瓶中采集拉曼光谱数据,每个样本连续采集3次。光谱的采集参数为:中心波长532 nm,平滑点数0,积分时间5 000 ms,功率等级9。
2.1.3 建模步骤
Step 1 根据10组安息香样本的拉曼光谱图,采用拉曼光谱强度直接分析安息香的质量浓度,判断该方法是否可行;
Step 2 选择角度转换方法,结合拉曼光谱将强度信号转换为角度值,建立安息香质量浓度快速分析模型;
Step 3 选取S1、S2、S3、S5、S7、S10这6组拉曼光谱数据作为建模样本,分析纯安息香光谱作为参比光谱,S4、S6、S8、S9作为验证样本;
Step 4 分析样本光谱与参比光谱,选择建模波长范围;
Step 5 对样本光谱进行求导降噪处理;
Step 6 采用自编算法计算得到样本光谱与参比光谱的系列夹角值θ;
Step 7 建立θ值与安息香质量浓度的关联方程,调整求导阶数直至相关系数r>0.990 0。
2.1.4 模型验证
将样本S4、S6、S8、S9的夹角值θ代入已经建好的模型中,算出其预测的溶液质量浓度,与样本的真实质量浓度相比较,验证模型的可行性。
2.2 安息香介稳区的测定
2.2.1 安息香在95%乙醇溶液中饱和溶解度的测定
将精密恒温反应浴的热力学温度设定为273.15 K,恒温,称取适量的安息香晶体放入圆底烧瓶中,加入一定量的95%乙醇,搅拌使安息香充分溶解,形成饱和溶液,静置,取少量上层清液于测量瓶中,采集拉曼光谱。每5 K重复以上步骤,直至温度达到343.15 K。将采集到的拉曼数据代入算法平台,用建模参数计算得到一系列夹角值,代入安息香质量浓度与夹角值θ的关联方程,计算得到的安息香质量浓度即为对应温度下的安息香饱和溶解度。
2.2.2 安息香在95%乙醇中过饱和溶解度的测定
由于安息香降温结晶时晶体生长速度较快,会出现在容器底部,肉眼可以观察到晶体的出现,因此本文采用目测法测定安息香的过饱和溶解度。
根据得到的安息香饱和溶解度,配制343.15 K下的安息香饱和溶液,当形成安息香饱和溶液后,在高于饱和温度5 K的温度点保温10 min,使晶体完全溶解,通过冷水浴降温,观察首批晶核出现时间,记录析晶点温度,用拉曼光谱采集此刻溶液光谱,在273.15~343.15 K范围内每降低5 K重复以上步骤。将光谱数据代入算法平台,计算得到各温度下的系列夹角值θ,代入关联方程中,得到不同温度下的安息香过饱和溶解度。
2.2.3 安息香在95%乙醇溶液中介稳区及模型拟合
修正后的Apelblat模型[16]如式(1)所示,
(1)
式中:x为安息香在95%乙醇溶液中的溶解度的数值,单位 g/L;A、B和C为方程的参数,可以通过实验数据关联得到;T为热力学温度的数值,单位 K。
采用修正后的Apelblat模型对饱和溶解度数据和过饱和溶解度数据进行关联,溶解度与超溶解度之间的温度差即为介稳区[17]。
2.3 安息香在95%乙醇溶液中的热力学数据计算
在工业结晶过程中,主要热力学参数有溶解热、溶解熵、吉布斯自由能与结晶热。其中溶解热是单位溶质晶体在溶剂中溶解时所吸收的热量,溶解的逆过程是结晶,生成单位质量溶质晶体所放出来的热量称为结晶热。绝大多数物质的稀释热很小,与溶解热相比可以忽略,因此可以认为结晶热等于负的溶解热[18]。在等压状态下,结晶热又叫结晶焓,溶解热也称为溶解焓,溶解焓与结晶焓存在以下关系[19]:
(2)
其中,溶解焓[ΔHdiss]的测定通常用优化后的van't Hoff 模型[20]计算,如式(3)所示,
(3)
式中:R=8.314 J/(mol·K),为通用气体状态常数;[ΔHdiss]与[ΔSdiss]分别为安息香溶解焓与溶解熵。由式(3)可知,安息香溶解度的自然对数(ln x)和温度T的倒数(1/T)存在线性关系,将ln x与1/T建立关联方程,通过方程斜率与截距可以求得安息香溶解焓[ΔHdiss]与溶解熵[ΔSdiss],进而可以得到安息香的结晶焓[ΔHcry]。
吉布斯自由能[ΔGdiss]的计算可以通过Gibbs-Heimholtz方程[21](式(4))计算得出,其中Tm为实验温度范围内的温度平均值。
(4)
3 結果与讨论
3.1 采用拉曼光谱强度直接分析安息香的质量浓度
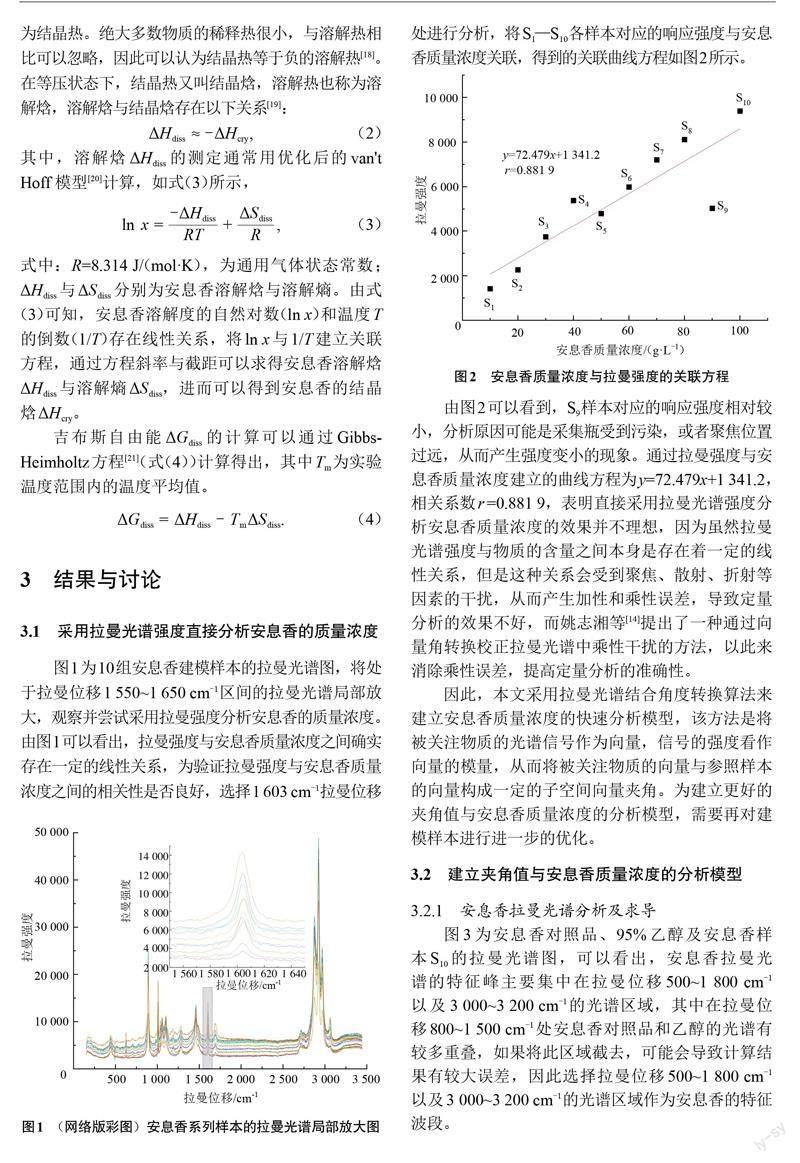
图1为10组安息香建模样本的拉曼光谱图,将处于拉曼位移1 550~1 650 cm-1区间的拉曼光谱局部放大,观察并尝试采用拉曼强度分析安息香的质量浓度。由图1可以看出,拉曼强度与安息香质量浓度之间确实存在一定的线性关系,为验证拉曼强度与安息香质量浓度之间的相关性是否良好,选择1 603 cm-1拉曼位移处进行分析,将S1—S10各样本对应的响应强度与安息香质量浓度关联,得到的关联曲线方程如图2所示。
由图2可以看到,S9样本对应的响应强度相对较小,分析原因可能是采集瓶受到污染,或者聚焦位置过远,从而产生强度变小的现象。通过拉曼强度与安息香质量浓度建立的曲线方程为y=72.479x+1 341.2,相关系数r =0.881 9,表明直接采用拉曼光谱强度分析安息香质量浓度的效果并不理想,因为虽然拉曼光谱强度与物质的含量之间本身是存在着一定的线性关系,但是这种关系会受到聚焦、散射、折射等因素的干扰,从而产生加性和乘性误差,导致定量分析的效果不好,而姚志湘等[14]提出了一种通过向量角转换校正拉曼光谱中乘性干扰的方法,以此来消除乘性误差,提高定量分析的准确性。
因此,本文采用拉曼光谱结合角度转换算法来建立安息香质量浓度的快速分析模型,该方法是将被关注物质的光谱信号作为向量,信号的强度看作向量的模量,从而将被关注物质的向量与参照样本的向量构成一定的子空间向量夹角。为建立更好的夹角值与安息香质量浓度的分析模型,需要再对建模样本进行进一步的优化。
3.2 建立夹角值与安息香质量浓度的分析模型
3.2.1 安息香拉曼光谱分析及求导
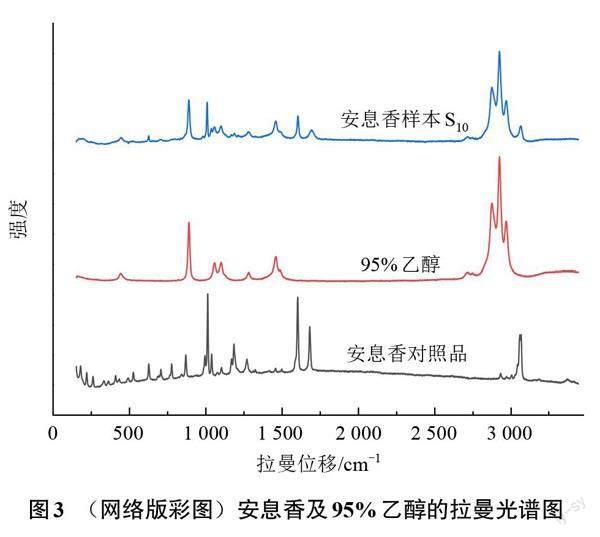
图3为安息香对照品、95%乙醇及安息香样本S10的拉曼光谱图,可以看出,安息香拉曼光谱的特征峰主要集中在拉曼位移500~1 800 cm-1以及3 000~3 200 cm-1的光谱区域,其中在拉曼位移800~1 500 cm-1处安息香对照品和乙醇的光谱有较多重叠,如果将此区域截去,可能会导致计算结果有较大误差,因此选择拉曼位移500~1 800 cm-1以及3 000~3 200 cm-1的光谱区域作为安息香的特征波段。
选取样本S10的拉曼光谱,分别进行0阶、1阶滤波求导降噪处理,处理后的拉曼光谱图如图4所示。可以看出,未进行滤波求导的拉曼光谱图特征峰较为明显且平滑,而1阶求导相对于0阶求导谱图,峰宽缩小,但分辨率较0阶求导反而降低,噪声相对增大。
3.2.2 关联方程的建立
为了建立最佳样本模型,选取S1、S2、S3、S5、S7、S10这6个样本作为模型的校正集,采用角度转换的方法,选择安息香分析纯拉曼光谱作为参比光谱,在利用MATLAB进行不同求导阶数条件下,选取全波段(152~3 443 cm-1)或特征波段(500~1 800 cm-1、3 000~3 200 cm-1)进行建模,得到系列光谱的夹角值θ,以安息香质量浓度为横坐标,夹角值为纵坐标,建立安息香的质量浓度与夹角值θ的关联方程,如表1所示。
由表1可知,全波段及特征波段未经求导的关联方程相关性分别为0.992 1与0.995 9,较其对应的1阶求导后的关联方程离散程度更小。这表明未经求导的原始光谱信号明显,1阶求导提高了噪音,降低了特征峰光谱信号,误差增大。相对于用角度转换算法全波段进行建模,截取特征波段忽略了其他光谱信号干扰,减小误差,提高了数据的准确性。
与拉曼强度与安息香质量浓度建立分析模型的方法相比,角度转换算法建模更能提高定量分析准确性,减小误差,相关性更好。综合考虑,本文选择用拉曼光谱结合角度转换算法进行建模,并选取r为0.995 9的处理条件b建立安息香的含量快速分析模型。
3.2.3 模型验证
将S4、S6、S8、S9这4组样本的拉曼数据导入MATLAB计算平台中,选取特征波段,求出对应的夹角值θ,代入关联方程y=-0.001 4x+0.236 1中,得到对应的预测质量浓度及与真实质量浓度的误差,结果如表2所示。
由表2可知,利用模型计算样本的质量浓度与样本的实际质量浓度的相对误差在-4.29%~3.37%,并且对于采用拉曼光谱强度分析安息香质量浓度时发现的异常谱图点S9,用该分析模型得到的预测质量浓度为86.62 g/L,与其真实质量浓度的相对误差较小,这表明采用拉曼光谱结合角度转换建立的安息香质量浓度快速分析模型精准度较高,对安息香质量浓度的预测能力较为准确。
3.3 安息香在95%乙醇中的介稳区宽度及溶解度数据关联
在273.15~343.15 K范围内,将不同温度下的安息香拉曼数据导入MATLAB计算平台中,截取特征波段,利用角度转化算法分别求出不同温度下,饱和溶液及过饱和溶液的拉曼光谱与分析纯安息香拉曼光谱之间的夹角值θ。将夹角值代入关联方程y=-0.001 4x+0.236 1中,可以直接求得不同温度条件下的安息香的饱和溶解度与过饱和溶解度。用Apelblat方程进行溶解度数据关联,建立曲线方程,过饱和溶解度曲线与饱和溶解度曲线之间的水平距离为介稳区宽度,结果如图5所示。
从图5可以看出,在实验温度范围内,安息香在95%乙醇中的饱和溶解度和过饱和溶解度都是伴随着温度的升高而增大,且增大的幅度不断增加,而且低温区域的介稳区宽度要比高温区域的介稳区宽度宽一些。这主要是因为温度升高,溶液黏度降低,溶质扩散系数增加,分子热效应加剧,使得分子间碰撞成核几率增大,介稳区宽度随之降低[22]。
将溶解度与温度的数据用Apelblat方程进行关联,可以得出安息香在95%乙醇中饱和溶解度曲线方程为:ln x=-62.5-1 736.6/T+12.3ln T,r =0.999 1;过饱和溶解度曲线为:ln x=-72.7-763/T+13.6ln T,r =0.999 0。
目前在热力学研究方面,常用的溶解度計算方法,是通过重量法多次测定待测物质质量,计算得到测量物质的饱和溶液摩尔分数。而本文是通过拉曼光谱结合角度转换算法建立安息香质量浓度分析模型,后续可以采集不同温度下任意安息香饱和溶液拉曼光谱,利用该模型直接计算出对应的安息香质量浓度。相比重量法而言,该方法具有操作便捷、准确性好、分析效率高等特点。
3.4 热力学数据的计算结果
将溶解度数据代入式(3),对安息香溶解度的自然对数ln x与1/T进行拟合,建立线性方程并得到图6。
由图6可知,拟合得到的线性方程为ln x=-5 691.2/T+20.884,相关系数r为0.993 2,根据式(3)计算可得,安息香在95%乙醇溶液中的溶解焓[ΔHdiss]=47.32 kJ/mol,溶解熵[ΔSdiss]=173.63 J/(mol·K),进而得到结晶焓[ΔHcry]为-47.32 kJ/mol,结晶焓为负数,说明安息香的结晶过程是放热过程。
计算得到实验温度范围内的热力学温度平均值Tm=308.15 K,再将溶解焓与溶解熵的值代入式(4),得到安息香溶解过程中吉布斯自由能[ΔGdiss]=-6.18 kJ/mol。则在测定温度范围内,安息香在95%乙醇溶液中的溶解过程是随着温度升高而吸热自发进行的反应过程。
4 结论
本文采用角度转换算法,结合拉曼光谱建立安息香结晶热力学分析方法,首先建立安息香质量浓度与夹角值的关联方程,通过采集安息香饱和溶液拉曼光谱数据,直接计算得到安息香在95%乙醇溶液中的溶解度,并用Apelblat方程关联溶解度曲线,通过van't Hoff 模型以及Gibbs-Heimholtz方程计算相关溶解热力学数据。
1)研究结果显示,建立关联方程的相关系数r为0.995 9,相对误差在-4.29%~3.37%,准确度较高,该方法具有建模样本少、检测时间短、分析效率高、操作简便、应用范围广等优点。
2)用Apelblat方程关联得到溶解度曲线,相关系数r分别为0.999 1与0.999 0,吻合良好。在实验温度范围内,温度越高,安息香的溶解度和过饱和溶解度越大。由于温度升高,使得分子间碰撞成核几率增大,安息香在95%乙醇溶液中的介稳区宽度变窄。
3)根据van't Hoff 模型以及Gibbs-Heimholtz方程,计算得到安息香在95%乙醇溶液中的溶解焓[ΔHdiss]为47.32 kJ/mol,结晶焓[ΔHcry]为-47.32 kJ/mol,溶解熵[ΔSdiss]为173.63 J/(mol·K),吉布斯自由能[ΔGdiss]为-6.18 kJ/mol,表明安息香的溶解过程是在升温状态下能够自发进行的吸热过程。
参考文献
[1] 文婷,王海蓉,黄唯,等.结晶过程晶体粒度分布控制研究进展[J].化学工业与工程,2021,38(4):44-55.
[2] NURWAHYUNI I,NABABAN B,PANGOLOI S,et al. Cinnamic acid in frankincense sap as a criterion for determining the best mother plant for vegetative propagation of Styrax benzoin (Sumatra benzoin) in Sumatra, Indonesia[J].International Journal of Forestry Research,2022,2022. Doi:10.1155/2022/4160241.
[3] 郭盛争,吴送姑,苏鑫,等.莱鲍迪苷A溶解度与介稳区宽度的测定及其结晶过程研究[J].化工学报,2021,72(8):3997-4008.
[4] 张红蕾,武耐英,乔宣宣,等.番茄红素晶体在正己烷-丙酮混合溶剂中的结晶热力学研究[J].中国食品添加剂,2021,32(12):135-140.
[5] LIU Y Z,GUO H J. Solubility determination and crystallization thermodynamics of an intermediate in different organic solvents[J].Journal of Molecular Liquids,2021,339.Doi:10.1016/j.molliq.2021.116821.
[6] 曹小雪,吉绍长,匡雯婕,等.甲醇-水溶剂中L-苯丙氨酸结晶热力学[J].化工学报,2019,70(4):1255-1262.
[7] ZHAO X H,WANG J L,CHEN L Z,et al. Crystallization thermodynamics of FOX-7 in three binary mixed solvents[J].Journal of Molecular Liquids,2019,295.Doi:10.1016/j.molliq.2019.111445.
[8] 郭恒杰,曹端林,党鑫,等. 1-甲基-3,4,5-三硝基吡唑的结晶热力学[J].含能材料,2018,26(6):511-516.
[9] ZHANG J Y,LIANG Z H,JI S C,et al. The thermal behavior of pyrazinamide in 12 solvents from 288.15 to 328.15 K[J].Journal of Molecular Liquids,2021,329. Doi:10.1016/j.molliq.2021.115572.
[10] LIU W J,GUO Y J,CHEN J X,et al. Measurement and correlation of the solubility of telmisartan (Form A) in nine different solvents from 277.85 to 338.35 K[J].Journal of Solution Chemistry,2016,45(6):932-946.
[11] AUSTGEN D M,ROCHELLE G T,PENG X,et al. Model of vapor-liquid equilibria for aqueous acid gas-alkanolamine systems using the electrolyte-NRTL equation[J].Industrial & Engineering Chemistry Research,1989,28(7):1060-1073.
[12] APELBLAT A,MANZUROLA E. Solubilities of L-aspartic, DL-aspartic, DL-glutamic, p-hydroxybenzoic, o-anisic, p-anisic, and itaconic acids in water from T=278 K to T=345 K[J].The Journal of Chemical Thermodynamics,1997,29(12):1527-1533.
[13] ZOU F X,ZHUANG W,WU J L,et al. Experimental measurement and modelling of solubility of inosine-5′- monophosphate disodium in pure and mixed solvents[J].The Journal of Chemical Thermodynamics,2014,77:14-22.
[14] 姚志湘,孙增强,粟晖,等.通过向量角转换校正拉曼光谱中乘性干扰[J].光谱学与光谱分析,2016,36(2):419-423.
[15] 粟晖,马金鸽,忻欣,等.拉曼光谱快速跟踪蔗糖水解過程组分含量及动力学研究[J].光谱学与光谱分析,2020,40(9): 2821-2825.
[16] WEI D W,PEI Y H. Solubility of diphenyl carbonate in pure alcohols from (283 to 333)K[J].Journal of Chemical and Engineering Data,2008,53(11):2710-2711.
[17] 毛娅,徐程浩,杨德建,等.乙醇-异丙醇-水体系中莱鲍迪甙A的溶解度与介稳区的测定[J].食品工业科技,2017,38(14):93-96.
[18] 周涛.化工原理[M].北京:科学出版社,2010.
[19] 刘跃文,王学魁,沙作良,等.L-丙交酯在不同有机溶剂中的溶解度测定[J].现代化工,2013,33(5):133-135.
[20] YANG G D,LI C,ZENG A G,et al. Solubility of imperatorin in ethanol plus water mixtures[J].Journal of Molecular Liquids,2012,167:86-88.
[21] ZHANG Q,HU Y H,SHI Y,et al. Thermodynamic models for determination of the solubility of dibenzothiophene in different solvents at temperatures from (278.15 to 328.15) K[J].Journal of Chemical and Engineering Data,2014,59(9): 2799-2804.
[22] 刘珏欣,郑承刚,叶世超.磷酸二氢钾结晶热力学数据的测定及应用研究[J].无机盐工业,2021,53(1):62-64.
Thermodynamics of benzoin crystallization based on the Raman
spectra combined angle conversion
MA Xin, LIU Anmin, YAO Zhixiang*
(School of Biological and Chemical Engineering, Guangxi University of Science and Technology, Liuzhou 545006, China)
Abstract: The curve equation of benzoin concentration and angle value was established by using Raman spectroscopy combined angle conversion algorithm. The saturation temperature of benzoin in 95% ethanol was observed at T=273.15~343.15 K by the static method and the direct-vision method. The measured spectral data was angle-converted to obtain a series of angular values, and the saturation solubility was directly obtained from the standard curve equation. The solubility data were correlated with the modified Apelblat equation, the metastable zone was plotted, and the relevant dissolution thermodynamic data were calculated by the van't Hoff model as well as the Gibbs-Heimholtz equation. The results show that the correlation coefficient of the established model equation was 0.995 9, and the relative error of the verified sample was between -4.29% and 3.37%. The solubility curve correlation coefficient r of the Apelblat equation fit was 0.999 1 and 0.999 0, the solubility and supersaturated solubility of benzoin in 95% ethanol increased with increasing temperature, while the width of the metastable zone decreased with increasing temperature. During the dissolution of benzoin crystals, the dissolution enthalpy was 47.32 kJ/mol, the crystals enthalpy was -47.32 kJ/mol, the dissolution entropy was 173.63 J/(mol·K), Gibbs free energy was -6.18 kJ/mol, so the dissolution process was a spontaneous endothermic reaction with increasing temperature. Compared with the commonly used weight method to obtain the solubility, this method is simple and fast. Therefore, the concentration of benzoin can be directly calculated by collecting the benzoin Raman spectra at different temperatures, which can be used for the thermodynamic analysis of various systems.
Key words: benzoin; crystallization thermodynamics; solubility; supersaturated solubility; metastable zone
(責任编辑:于艳霞)
收稿日期:2022-11-17
基金项目:广西自然科学基金项目(2015GXNSFAA139038);广西重点研发计划项目(桂科AB16380348)资助
第一作者:马鑫,在读硕士研究生
*通信作者:姚志湘,博士,教授,研究方向:化工过程分析技术,E-mail:zxyao@gxust.edu.cn
