基于多目标混合进化算法的作业车间混排可变分批节能调度方法
2023-12-02谢法吾李玲玲李丽黄洋鹏
谢法吾 李玲玲 李丽 黄洋鹏
摘要:
针对作业车间分批调度问题,集成可变子批划分和子批混排策略,考虑批量划分约束、子批混排加工约束等,建立了最小化能耗和完工时间的混排可变分批调度优化模型,并提出了一种改进多目标混合进化算法。为了协调算法的全局搜索与局部搜索性能,将Jaya算法种群更新机制引入基于分解的多目标进化算法中,同时结合混排可变分批调度问题特征,设计了一种基于子批拆分/合并与关键链相结合的局部搜索策略。基于不同规模算例,对比分析了所提出的算法与其他经典算法的求解性能。实验结果表明,所提出的算法在Pareto解集收敛性和分布性方面具有明显优势,同时所提出的混排可变分批策略可有效降低能耗、缩短完工时间。
关键词:作业车间;分批调度;可变分批;子批混排;进化算法
中图分类号:TH162
DOI:10.3969/j.issn.1004-132X.2023.13.007
Energy-efficient Job Shop Scheduling with Variable Lot Splitting and Sublots Intermingling Based on Multi-objective Hybrid Evolutionary Algorithm
XIE Fawu LI Lingling LI Li HUANG Yangpeng
College of Engineering and Technology,Southwest University,Chongqing,400715
Abstract: For solving the lot streaming job shop scheduling, a strategy was presented integrating variable sublots splitting and sublots intermingling, and a multi-objective optimization model of lot streaming scheduling was established to minimize the energy consumption and makespan. An improved multi-objective hybrid evolutionary algorithm was presented. In order to balance the global and local searching ability of the algorithm, the population updating mechanism of the Jaya algorithm was incorporated into the decomposition based multi-objective evolutionary algorithm. Considering the scheduling characteristics of variable lot splitting and sublots intermingling, a local searching strategy was designed integrating lot splitting/merging with critical path. The performance of the proposed algorithm and the state-of-the-art algorithms were compared under a set of instances of different scales. Experimental results show that the proposed algorithm has good performance on the convergence and distribution of Pareto solution sets. Moreover, the proposed variable lot splitting and sublots intermingling strategy may effectively reduce the energy consumption and makespan.
Key words: job shop; lot streaming scheduling; variable lot splitting; sublots intermingling; evolutionary algorithm
收稿日期:2022-10-12
基金项目:
国家自然科学基金(51905449,51875480);重庆市自然科学基金(cstc2020jcyj-msxmX0127);中央高校基本科研业务费专项资金(SWU-KT22023)
0 引言
在全球能源成本飙升和环境日益恶化的形势下,绿色节能的生产方式已成为制造领域的关注热点。车间调度作为制造系统生产控制的重要组成部分,是影响生产效率、成本的关键环节,同时调度方案将对车间能源消耗产生显著影响。在开展生产调度优化时,兼顾能源消耗、环境排放等绿色指标以及完工时间、延期交货时间等经济性指标,已成为绿色制造背景下的热点研究问题。
国内外学者从不同角度出发,对流水车间[1-4]、作业车间[5-9]的节能调度问题开展了深入研究。其中,一类研究主要从机器分配和工序排序這两个子问题优化入手[1,3,5,7],以达到生产节能的目的。第二类研究则在机器分配和工序排序的基础上,引入了开/关机策略[2,8]、机器加工速度调节[9]以及分时电价机制[4],以最大化地降低能耗。现有的节能调度研究中,一部分研究聚焦于降低能耗[5],另一部分研究在考虑能耗目标的同时,还兼顾了完工时间[7,9]、延期交货时间[3,6]、成本[4]等经济性指标。节能调度问题的求解算法包括遗传算法[6,9]、进化算法[1,2,4]、人工蜂群算法[7]、Jaya算法[3]等。
考虑到生产实际中存在的工件批量性以及批次可分特性,将分批策略与调度优化相结合,可进一步缩短完工时间、提高设备利用率和生产效率。目前,分批调度研究主要面向流水车间[10-13],只有少部分研究围绕作业车间分批调度问题[14-15]展开。同时,现有的分批调度研究较多着眼于完工时间[13-14]等经济性指标。近年来,节能分批调度优化问题开始受到国内外学者的关注并取得了初步成果[10-12,15]。现有的节能分批调度研究,根据车间类型分为流水车间[10-11,15]和作业车间[15];按批量划分策略分为一致子批[10,12,15]和可变子批[11]两种类型;根据子批排序类型不同,分为混排[12,15]和非混排[10-11]两种。例如,PAN等[10]以分布式流水作业车间为对象,采用一致子批和非混排策略,并考虑能耗和完工时间目标,提出了一种基于Jaya算法的多目标分批调度优化方法。LIU等[11]考虑能耗、完工时间和延期交货时间目标,基于可变子批和非混排策略,建立了混合流水作业车间分批调度模型,并采用多目标进化算法进行了求解。CHEN等[12]以能耗和完工时间最小化为目标,考虑一致子批和混排策略,提出了基于改进遗传算法的混合流水车间分批调度方法。李聪波等[15]以柔性作业车间为研究对象,考虑能耗和完工时间目标,提出了基于一致子批和混排策略的作业车间分批调度节能优化方法。
现有的作业车间分批调度优化研究未考虑可变子批划分与子批混排策略的集成影响。对于多品种、中小批量的作业车间,由于各工件批量大小差异性以及工艺路线的离散性,将可变子批划分和子批混排策略相结合可进一步增加调度的灵活性,由此缩短机器空闲时间、提高机器利用率,并降低能耗。因此,基于可变子批划分与子批混排策略研究作业车间节能分批调度优化问题具有重要意义。然而,由于同时涉及可变子批划分与子批混排问题,要求各工件在各工序上的子批划分方案各不相同,且同一工件的各子批任务之间允许其他工件子批的混排加工,因此该调度问题相比于一致分批和非混排调度问题更加复杂。鉴于此,本文以多品种、中小批量的作业车间为研究对象,基于可变子批划分和子批混排策略,考虑能耗和完工时间目标,建立作业车间混排可变分批节能调度优化模型,并提出一种改进多目标混合进化算法求解该问题。为了协调算法的全局搜索与局部搜索能力,将Jaya算法种群更新机制引入基于分解的多目标进化算法中,同时结合混排可变分批调度问题特征,设计了一种基于子批拆分/合并与关键链相结合的局部搜索策略。最后基于不同规模算例,对比分析了所提出算法与其他经典算法的求解性能,以验证所提出算法的有效性和优势。
1 调度问题描述及数学建模
1.1 问题描述
为更好地描述混排可变分批的作业车间节能调度问题,本文定义了表1所示的符号及其含义。问题描述如下:作业车间中共有K台机器M={Mk|k=1,2,…,K}和I个待加工工件J={Ji|i=1,2,…,I};每个工件Ji由一批相同零件Pi={Pi,r|r=1,2,…,Ni}组成;每个工件的所有Ni个零件均需经过ni道工序加工,且每个工件的每道工序所选择的机器是已知且确定的。每个工件Ji在第j道工序上加工时,可被拆分为ui,j个子批,且每个子批s(s=1,2,…,ui,j)所包含的零件数目为wi,j,s。采用可变子批划分策略时,同一个工件在各工序上被划分的子批数量ui,j及各子批的批量大小wi,j,s不尽相同,即同一个零件Pi,r在不同工序上将被分配到不同的子批中。采用子批混排策略时,同一台机器上的同一个工件的各子批之间允许其他工件子批的插入加工。
调度以总能耗和完工时间最小为目标,确定可变子批划分方案和子批混排调度方案。其中,可变子批划分方案是确定各工件在每道工序上划分的子批数量ui,j以及每个子批的批量大小wi,j,s(s=1,2,…,ui,j);子批混排调度方案是确定所有子批在各机器上的混排加工顺序χi,j,s,k。
该调度问题的假设条件描述如下:
(1)所有工件在零时刻到达,所有机器在零时刻处于可用状态;
(2)同一个子批中的所有零件必须连续加工,不可被其他子批的零件中断;
(3)同一台机器加工相邻两个不同工件子批时将产生辅助操作(更换模具、夹具等)时间,且辅助操作必须在子批到达机器后才可开始;
(4)当一个子批中的所有零件均结束当前工序的加工后才可被运输至下一道工序所对应的机器上;
(5)每台机器在任一时刻只能加工一个子批的一个零件;一个零件同一时刻只能被一台机器加工。
3 试验结果与分析
MOJA/D算法采用Python3.8编程,运行环境为2.20 GHz PC,8 GB RAM,Windows10,64位操作系统,Intel Core i5 CPU。
为了验证算法性能,选用La01~La15(Lawrence)共15个算例,工件种类I={10,15,20},工序总数n=5,机器总数K=5。算例中相关参数设置如表2所示。
3.1 参数设置
采用正交试验设计确定最优算法参数。
MOJA/D算法参数包括:种群数量L、邻域个数T、交叉概率Pc以及变异概率Pm。每个参数设置3个水平,如表3所示。为了验证4种算法参数对MOJA/D算法性能的影响,选用La06算例,在每种参数组合下运行10次,得到IGD(inverse generational distance)平均值,结果如表4所示。其中,IGD的数值越小,表示算法性能越优。
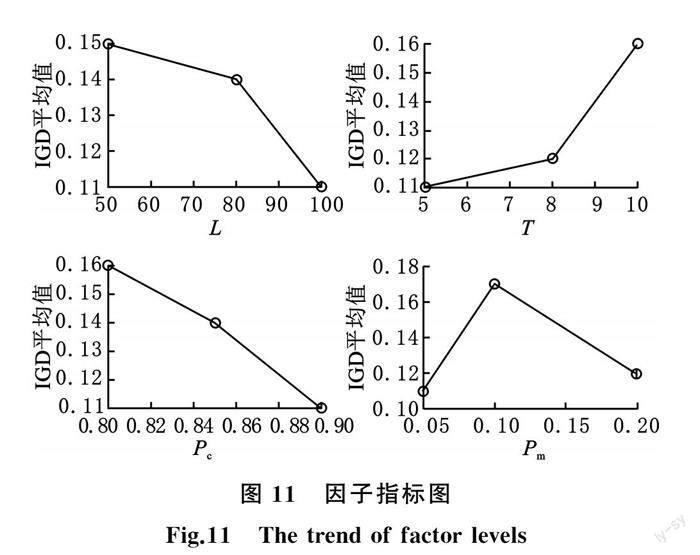
基于表4的数据,利用极差分析计算各参数L、T、Pc以及Pm在各個水平下的均值,如表5所示。根据表5绘制出各个参数的水平均值,如图11所示。由图11可知,随着种群数量的增大,IGD平均值不断减小,这是因为种群的数量越大得到的解集就更均匀、更广泛;随着邻域数量的增大,IGD平均值不断增大,主要是因为Jaya在邻域内进行更新时容易使邻域内的解都集中到其中最优个体的附近,进而影响整个种群的解集分布,而更大的交叉概率和更小的变异概率有利于提高种群解集的均匀性。由图11可以确定最优的算法参数组合为:L=100,T=5,Pc=0.9以及Pm=0.05。
3.2 局部搜索有效性验证
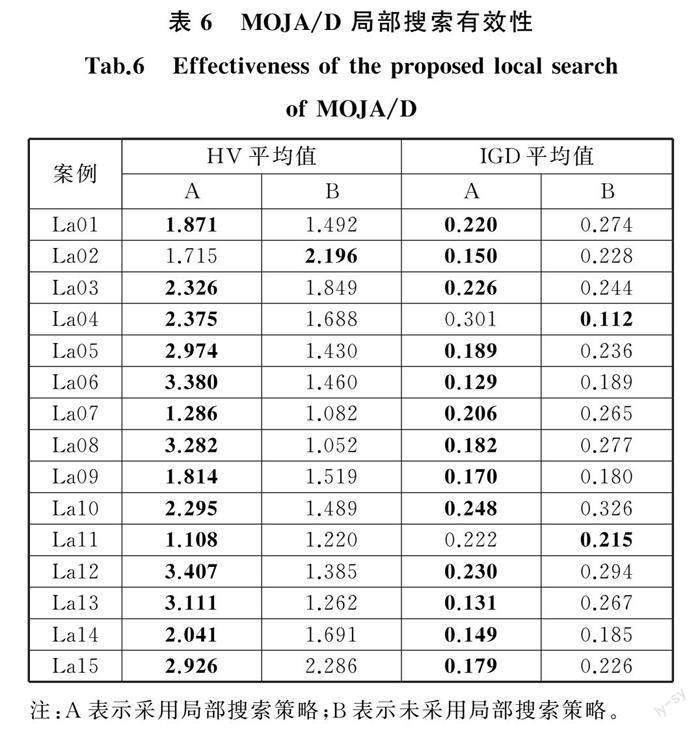
为验证所设计的局部搜索策略的有效性,选用La01~La15共15组算例,在每个算例下,分别将采用局部搜索与未采用局部搜索的MOJA/D算法运行10次,得到了HV(hyper volume)和IGD平均值,如表6所示。其中,HV平均值越大、IGD平均值越小,表示Pareto解集的分布性和收敛性越好。
由表6的HV数据可以看出,未采用局部搜索的MOJA/D仅在算例La02中的表现更好,而采用了局部搜索的MOJA/D在剩余14个算例中有更好的表现。从表6的IGD数据可以看出,在除La04和La11以外的13个案例中,采用了局部搜索的MOJA/D表现优于未采用局部搜索的MOJA/D。
图12a和图12b分别展示了HV和IGD箱线图对比情况。由图12可知,采用局部搜索策略得到的Pareto解集明显优于未采用局部搜索策略的Pareto解集,由此验证了所设计的局部搜索策略的有效性。
3.3 算法性能对比
为了进一步验证MOJA/D算法的有效性,将MOJA/D与MOEA/D、Jaya、NSGA-Ⅱ对比分析。同样选用La01~La15共15组算例,每个算例下分别运行每种算法10次,得到了4种算法的HV和IGD平均值,分别如表7和表8所示。可以看出,所提出的MOJA/D算法在大部分算例(除La01、La04、La09、La11和La14以外)中的表现均优于MOEA/D、Jaya、NSGA-Ⅱ算法。
图13a和图13b分别展示了4种算法的HV和IGD箱線图对比情况。由图13可知,相较于MOEA/D、Jaya、NSGA-Ⅱ,MOJA/D能获得较大的HV值和较小的IGD值,由此说明MOJA/D在解集收敛性和分布性方面表现更优。
图14展示了4种算法分别求解6个算例(La01、La03、La05、La9、La13和La15)所获得的Pareto前沿。由图14可以看出,MOJA/D算法所得的Pareto前沿在大多数情况下均支配了MOEA/D、Jaya和NSGA-Ⅱ的Pareto前沿。此结果说明所提出的MOJA/D算法在求解多目标优化问题上具有优越性。
3.4 混排可变分批调度方法有效性验证
为了验证所提出的混排可变分批调度方法的有效性,选用La01~La15共15组算例,将可变分批+子批混排策略与可变分批+子批非混排策略的节能效果以及完工时间数据作对比分析,具体数据如表9所示。
由表9可以看出,相比于非混排策略,采用子批混排策略时,所有算例的能耗均有显著降低;同时,在除La03和La07以外的其他13个算例中,子批混排策略相较于非混排策略可有效缩短完工时间。由此可知,可变分批+子批混排策略在降低能耗、缩短完工时间上明显优于可变分批+子批非混排策略。究其原因,将可变子批(如子批拆分、子批合并)与子批混排相结合,一方面可有效缩短机器空闲时间,由此缩短完工时间(见图15和图16);另一方面,随着机器空闲时间的缩短,机器空闲时段能耗随之降低,同时由于混排可变分批增加了调度的灵活性,通过协同优化工件分批方案与子批混排调度方案可有效减少机器辅助操作能耗、子批运输能耗。由此可知,将可变分批和子批混排策略应用到多品种批量生产的作业车间中,可有效降低能源消耗、提高生产效率。
4 结论
(1)本文针对作业车间分批调度问题,基于混排可变分批策略,以可变分批划分方案和子批混排调度方案为集成优化变量,建立了最小化能耗和完工时间目标的作业车间多目标调度优化模型。
(2)将Jaya算法种群更新机制引入基于分解的多目标进化算法中,以提高种群多样性;结合混排可变分批调度问题特征,设计了一种基于子批拆分/合并与关键链相结合的局部搜索策略,以协调算法的全局搜索与局部搜索。
(3)选取不同规模算例,验证了所设计的局部搜索策略的有效性;对比分析了所提出算法(MOJA/D)与MOEA/D、Jaya、NSGA-Ⅱ算法在不同规模算例下的求解性能,结果表明MOJA/D在解集收敛性和分布性方面具有明显优势;对比分析了不同算例下混排可变分批策略相较于非混排可变分批策略的节能效果。
(4)后续研究可将混排可变分批调度方法扩展到更为复杂的生产系统中(如动态生产环境),并添加更多约束以贴近实际生产,同时进一步提高算法的求解性能。
参考文献:
[1] WANG G C, LI X Y, GAO L, et al. Energy-efficient Distributed Heterogeneous Welding Flow Shop Scheduling Problem Using a Modified MOEA/D[J]. Swarm and Evolutionary Computation, 2021, 62:100858.
[2] XIN X, JIANG Q Q, LI C, et al. Permutation Flow Shop Energy-efficient Scheduling with a Position-based Learning Effect[J]. International Journal of Production Research, 2023, 61(2):382-409.
[3] ZHAO F Q, MA R, WANG L. A Self-learning Discrete Jaya Algorithm for Multiobjective Energy-efficient Distributed No-idle Flow-shop Scheduling Problem in Heterogeneous Factory System[J]. IEEE Transactions on Cybernetics, 2021, 52(12):12675-12686.
[4] LIU M, YANG X N, CHU F, et al. Energy-oriented Bi-objective Optimization for the Tempered Glass Scheduling[J]. Omega International Journal of Management Science, 2020, 90:101995.
[5] RAKOVITIS N, LI D, ZHANG N, et al. Novel Approach to Energy-efficient Flexible Job-shop Scheduling Problems[J]. Energy, 2021, 238:121773.
[6] HE L, CHIONG R, LI W, et al. Multiobjective Optimization of Energy-efficient Job-shop Scheduling with Dynamic Reference Point-based Fuzzy Relative Entropy[J]. IEEE Transactions on Industrial Informatics, 2022, 18(1):600-610.
[7] JIANG X Y, TIAN Z Q, LIU W J, et al. Energy-efficient Scheduling of Flexible Job Shops with Complex Processes:a Case Study for the Aerospace Industry Complex Components in China[J]. Journal of Industrial Information Integration, 2022, 27:100293.
[8] GONG G L, CHIONG R, DENG Q W, et al. Energy-efficient Production Scheduling through Machine On/Off Control during Preventive Maintenance[J]. Engineering Applications of Artificial Intelligence, 2021, 104:104359.
[9] DUAN J G, WANG J H. Energy-efficient Scheduling for a Flexible Job Shop with Machine Breakdowns Considering Machine Idle Time Arrangement and Machine Speed Level Selection[J]. Computers and Industrial Engineering, 2021, 161:107677.
[10] PAN Y X, GAO K Z, LI Z W, et al. Solving Biobjective Distributed Flow-shop Scheduling Problems with Lot-streaming Using an Improved Jaya Algorithm[J]. IEEE Transactions on Cybernetics, 2022, 32(6):3818-3828.
[11] LIU J Q, TAO X R, JIA B X, et al. Efficient Multi-objective Algorithm for the Lot-streaming Hybrid Flowshop with Variable Sub-lots[J]. Swarm and Evolutionary Computation, 2020, 52: 100600.
[12] CHEN T L, CHENG C Y, CHOU Y H. Multi-objective Genetic Algorithm for Energy-efficient Hybrid Flow Shop Scheduling with Lot Streaming[J]. Annals of Operations Research, 2020, 290:813-836.
[13] ZHANG B, PAN Q K, MENG L L, et al. An Automatic Multi-objective Evolutionary Algorithm for the Hybrid Flow Shop Scheduling Problem with Consistent Sublots[J]. Knowledge Based Systems, 2022, 238:107819.
[14] LI L L. Research on Discrete Intelligent Workshop Lot-streaming Scheduling with Variable Sublots under Engineer to Order[J]. Computers and Industrial Engineering, 2022, 165:107928.
[15] 李聰波, 沈欢, 李玲玲. 面向能耗的多工艺路线柔性作业车间分批优化调度模型[J]. 机械工程学报, 2017, 53(5):12-23.
LI Congbo, SHEN Huan, LI Lingling. A Batch Splitting Flexible Job Shop Scheduling Model for Energy Saving under Alternative Process Plans[J]. Journal of Mechanical Engineering, 2017, 53(5):12-23.
[16] ZHANG Y H, GONG, Y J, GU T L, et al. DECAL:Decomposition-based Coevolutionary Algorithm for Many-objective Optimization[J]. IEEE Transactions on Cybernetics, 2019, 49(1):27-41.
[17] CALDEIRA R H, GNANAVELBABU A. Solving the Flexible Job Shop Scheduling Problem Using an Improved Jaya Algorithm[J]. Computers & Industrial Engineering, 2019, 137:106064.
[18] FAN J X, LI Y L, XIE J, et al. A Hybrid Evolutionary Algorithm Using Two Solution Representations for Hybrid Flow-shop Scheduling Problem[J]. IEEE Transactions on Cybernetics, 2021, 53(3):1752-1764.
[19] HAN Y Y, GONG D W, JIN Y C, et al. Evolutionary Multiobjective Blocking Lot-streaming Flow Shop Scheduling with Machine Breakdowns[J]. IEEE Transactions on Cybernetics, 2017, 49(1):184-197.
(编辑 王旻玥)
作者简介:
谢法吾,男,1996年生,硕士研究生。研究方向为智能优化和调度算法。E-mail:fawuxie@email.swu.edu.cn。
李玲玲(通信作者),女,1989年生,博士、讲师。研究方向为智能优化和调度算法。E-mail:lingzithyme@swu.edu.cn。
