Structural origin for composition-dependent nearest atomic distance in Cu–Zr metallic glass

Chi Zhang(张驰), Hua-Shan Liu(刘华山), and Hai-Long Peng(彭海龙)

School of Materials Science and Engineering,Central South University,Changsha 410083,China

Keywords: metallic glass,structure,molecular dynamics

1.Introduction

Disorder nature for the structure of metallic glass endows it with outstanding mechanical and physical properties compared with the crystalline counterpart.[1–4]Understanding the atomic-level structure is not only meaningful for unveiling the mystery of atomic packing in physics, but also important for tailoring the properties of metallic glasses via tuning the structure in materials science.Structural model for the disordered material can be traced back to 1960s, which is known as the dense-random-packed model for the structure of liquids.[5,6]It is soon applied to monoatomic metallic glass,[7]since both the liquid and glass show a similar structural profile in pair correlation function.This model essentially only concerns the packing in geometry by assigning a hard-spherelike diameter to atoms.Thus,the structure of metallic glass of multicomponent can be simplified into the densely packed hard spheres with different diameters, among which the binary metallic glass can been well resolved.[8,9]

However,the hard-spherelike model neglects the fact that atoms may form some kinds of clusters or aggregates that are locally denser and energetically stable.[10,11]One of the well-known clusters is the icosahedral polyhedron.Icosahedral clusters were firstly proposed as the stable local structures,explaining the undercooling capability of metallic liquids.[12]It is commonly reported in metallic glass,and found to play an important role in forming glass.[13–15]The icosahedral clusters have been recognized as one of most important topological short-range orders(SROs).

As metallic glass is usually compounded with different elements, the distribution of different atomic species in local environment can induce the so-called chemical short-range order(CSRO),which comes on the top of the topological SRO.CSRO characterizes how the local chemical concentration deviates from the random mixing, resulting from the strong chemical interaction between different atomic species.A peculiar phenomenon dictating the nontrivial effect of the chemical interaction on SRO is the shift of the first peak positions in pair distribution functions (PDFs), or the average nearest atomic distance,with composition.For instance,the effective nearest atomic distance deviates from the one in pure elements in Zr–Cu–Al glass,[16]Ni–Zr glass,[17]and Co–Sn alloy.[18]A composition-dependent nearest atomic distance has also been reported in Au–Al and Zr–Ni–Al melts.[19,20]This finding is strongly in contrast to the hard-spherelike model, as atoms cannot be treated as hard spheres with constant diameters.

Since long-range packing is built on the basis of shortrange order, resolving the concentration-dependent nearest atomic distance is crucial to unveil the structure of metallic glass containing components of chemical interaction.However, so far the detailed knowledge about the effect of local packing on it is still lacking.

In this study, we perform classical molecular-dynamics(MD)simulations on Cu–Zr metallic glass(MG).CuZr MG is a prototype of metallic glass that has been widely investigated both experimentally and numerically.[10,15,21–23]The structure of the metallic glass is studied systematically by changing the compositions, i.e., the Cu molar fraction increasing from 0.24 to 0.85.We observe the composition-dependent nearest atomic distance for Zr atoms, which monotonically increases with Cu concentration increasing.We rationalize this as the consequence of a composition-dependent chemical environment, which leads to the change of the population of local polytetrahedral packings, i.e., the quadrilateral, pentagonal,hexagonal,and heptagonal bipyramids,with Cu concentration.

2.Simulation details

MD simulations were performed by using the software large-scale atomic/molecular massively parallel simulator(LAMMPS)package.[24]We conducted MD simulations in a cubic box containing 5000 atoms with the embedded atom method(EAM)type of Cu–Zr interatomic potential developed by Mendelev.[25]The molar fraction of Cu atoms in the mixtures was defined as the concentrationcCu,with eight compositions studied here, i.e.,cCu=0.24, 0.33, 0.41, 0.50, 0.59,0.67,0.76,and 0.85.Computer simulations started at 2200 K in a random configuration for the positions of atoms.After a short-time equilibrium,samples were cooled down to 300 K at 19 K/ps in NPT ensemble (which has constant particle number,zero pressure,and linearly scaled temperature with time)under periodic boundary conditions applied to all the dimensions.At 300 K,the box length was set to the value that gives zero pressure.Finally,we switched to the canonical ensemble(NVT)to collect data.The time step was set to 1 fs in all the simulations.

3.Results and discussion

The microscopic information of the liquids can be given by the partial pair distribution functions (PDFs),gαβ(r),which measures the probability of finding an atom of typeβaround the central atom of typeαat a distancerin statistics.It can be calculated from

whereNrepresents the number of atoms,Vthe volume of the cubic model,andnαβ(r)the number of atoms of speciesβin the sphere range fromrtor+∆raround the atom of speciesα.Figure 1 shows the total PDF,g(r)=∑αβ cαcβgαβ(r),the partial PDFs,gCuCu(r),gCuZr(r),gZrZr(r), and the first peak positionrmaxing(r)s for different compositions.In the Cu–Zr system,the typical feature of amorphous structure appears,that is, the second peak is cleaved.[20,26,27]Panet al.found that the splitting of the second peak is related to the imbalance between the cluster connection mode and cluster compaction mode by analyzing the nearest neighbor clusters.[28]

With the increase ofcCu, a systematic shift towards smaller distance is found forg(r) at the first peak positions for all pairs, with a significant split occurring atcCur<0.50.These are caused by the difference in atomic size between Zr atom and Cu atom (the atomic diameter ratio about 1.25 according to the Goldschmidt radii,R(CN12)).[29]When the smaller Cu atoms gradually substitute for the larger Zr atoms,the interatomic distance transits from the diameter of Zr atoms to the one of Cu atoms,inducing a sudden jump for the average nearest atomic distance for all pairs(pentagon symbols in Fig.1(b)).This effect,however,should disappear if one concerns the first peak position of the partial PDFs in the hardsphere approximation.This is verified as the first peak positions ingCuCu(r) and thegCuZr(r) are insensitive to the concentration (Fig.1(b)).These peak positions of thegCuCu(r)and thegCuZr(r)are similar and compatible with empirical covalent radii,rmax,CuCu≈RCu+RCu,rmax,CuZr≈RCu+RZr, if one adopts the Goldschmidt radii,[29]RCu≈1.276 ˚A,RZr≈1.597 ˚A.They are almost unaffected bycCu.In contrast, a remarkable systematic change is seen in thegZrZr(r): upon increasingcCu, the nearest-neighbor peak shifts to large distance.A similar phenomenon has been reported in systems of strong chemical interactions, to that in Zr–Ni melt[30]and in the Al–Au melt.[19]

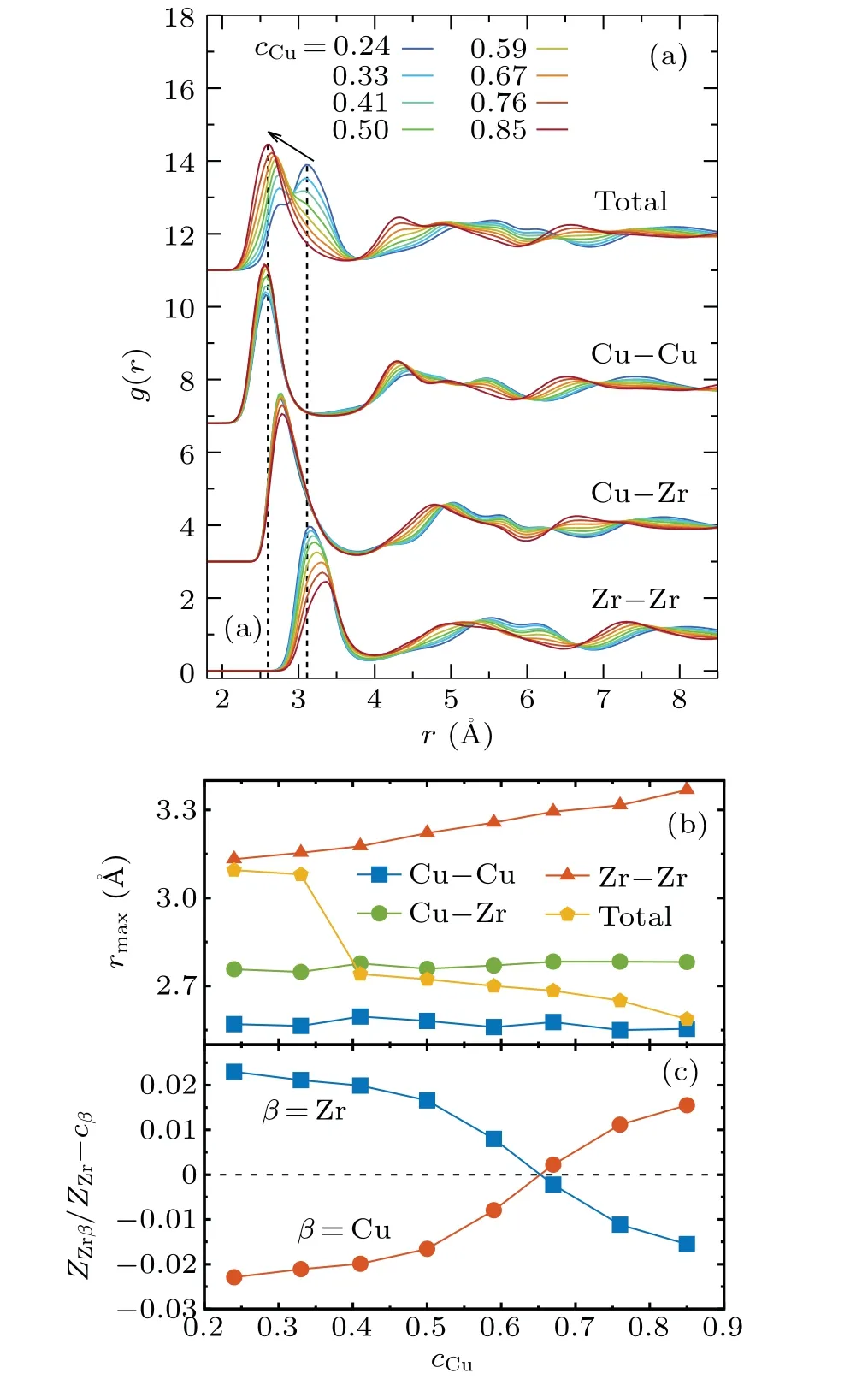
A similar assignment of the covalent radius to Zr atoms fails: at Cu-rich compositions,the first peak distance is larger than the one expected from the covalent radius.Explicitly, atcCu>0.5,rmax,ZrZr>RZr+RZr.The dependence of the first peak position of thegZrZr(r)on composition highlights that the Zr–Zr nearest neighbor pairs are sensitive to chemical environment.Indeed,the first peak ofgZrZr(r)is related to the nearest neighbor atoms,corresponding to the short-range order(SRO).The inecrease at the first peak position and the decrease in the first peak amplitude reflect the increase in the SRO.[31]

To demonstrate the chemical effect,we calculate the partial coordination number,Zαβ.It measures the average number of neighbors of speciesβaround a central atoms of speciesα

whereρis the average number density,cβis the concentration of atoms of typeβ,andrcis the distance of the first minimum in the partial radial distribution function.The total coordination number for the centralαatoms isZα=∑β Zαβ.In the case of random mixing, the neighbors around a central atom are randomly chosen according to the species concentration.This givesZαβ/Zα-cβ=0.

Figure 1(c)shows the calculated results ofZαβ/Zα-cβin the mixtures.Interestingly, it is found that the chemical concentration around Zr atoms is composition-dependent: the distribution probability of Zr neighbors is higher than the random mixing at Zr-rich compositions, while it is lower at Curich compositions.As a compensation,Cu atoms have a lower coordinating propensity at Zr-rich side, while have a higher propensity at Cu-rich side.The change of chemical environment can be related to the change of the Zr–Zr nereast distance, as the strong affiliating tendency of the smaller Cu atoms can,to some extent,squeeze the bigger neighboring Zr atoms outwards around the central Zr atoms.

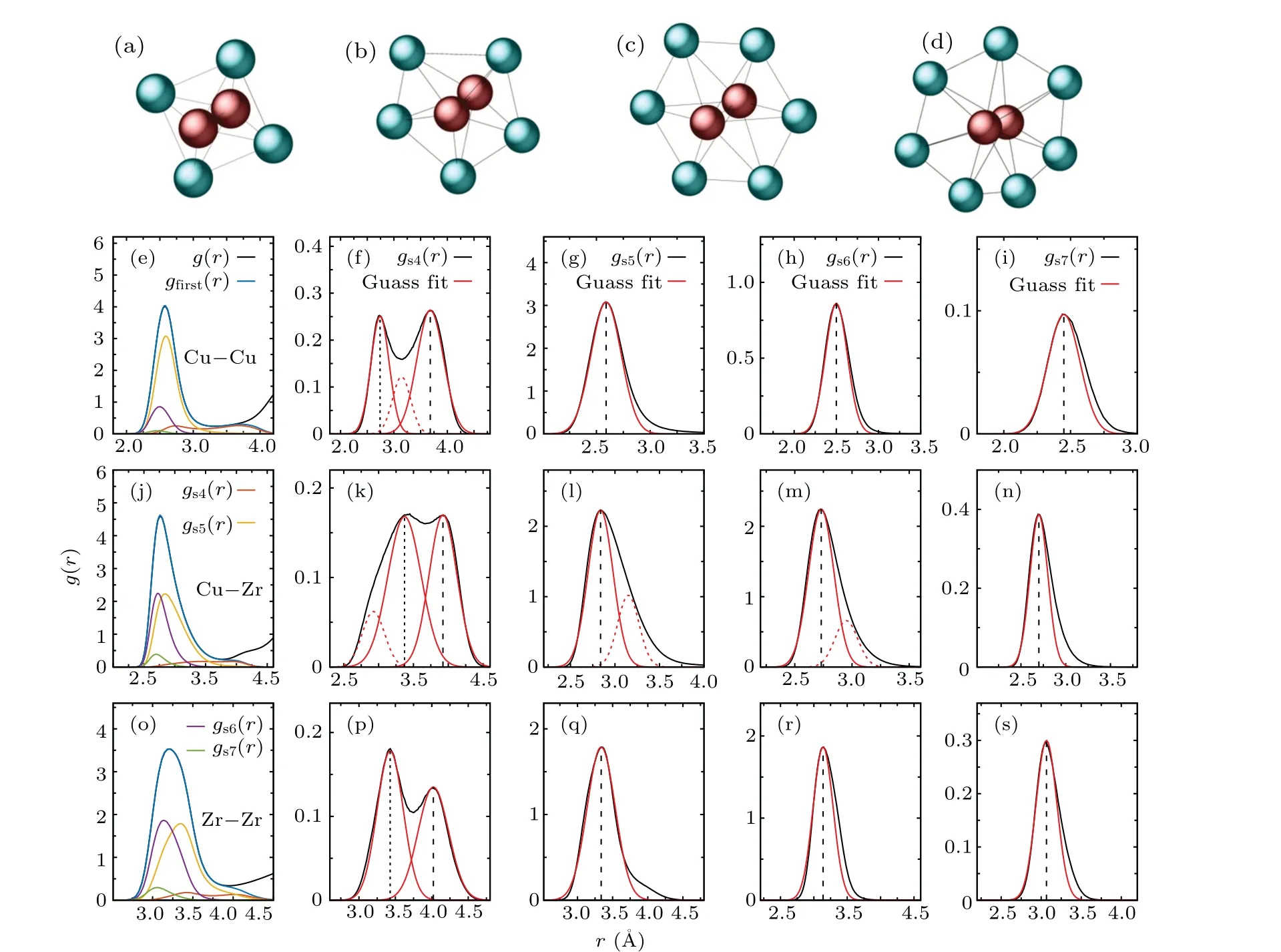
To unveil the detailed microscopic structural changes that lead to the increase of the nearest distance between Zr atom and Zr atom,we decompose the first peak ofgαβ(r)according to the Voronoi tessellation:[32]gfirst(r)represents the contribution of two atoms nearest connected(i.e.,their atomic distance is less thanrc)togαβ(r).This follows the analysis of the connections between clusters.[28]Thegsi(r)is the contribution of the two connected central atoms sharingi-number common neighbors togfirst(r).Figures 2(a)–2(d) illustrate the atomic structures for the 4-, 5-, 6-, and 7-number sharing neighbors.Figures 2(e), 2(j), and 2(r)demonstrate the decomposition ofgCuCu(r),gCuZr(r), andgZrZr(r) with standard deviation for amorphous alloy Cu50Zr50.Thegfirst(r) reproduces the first peak ofgαβ(r) well.It can be seen that the main contribution ofgCuCu(r) comes fromgs5(r)[33]andgs6(r) (as whose amplitudes are much larger than that ofgs7(r)andgs4(r)).

Thegsi(r)curves can be described by Gaussian function.Among themgs4(r) has two main peaks, e.g., with one located at 2.7 ˚A and the other at 3.7 ˚A for Cu–Cu pairs.Obviously, the latter is not a close-packed structure for two nearest neighbors,as its position is around the first minimum distance that separates the first neighbor shell from the second neighbor shell.Multi-peaks also emerge for Cu–Zr and Zr–Zr pairs ings4(r), indicating the 4-number sharing structure can be loosely packed.By contrast,the peaks can be predominantly reproduced by a single Gaussian function for 5-,6-,and 7-number sharing situations in all the atomic pairs.

Packing efficiencies for different kinds of number-sharing structures can be characterized by the average distance for the two connected central atoms.The positions of the Gaussian peak,rp,contributing to the first peak forg(r)in Cu–Cu pair,Cu–Zr pair, and Zr–Zr pair are shown in Fig.3.As the number of shared atoms increases, the distance between the two central atoms decreases,indicating more closely packed structures.When the number of shared atoms is small (like 4-number shearing structures), the distance between the neighboring central atoms is much larger than the expected radius based on the Goldschmidt radii[29]for all the atomic pairs.As the number of shared atoms increases, the discrepancy gradually disappears.This implies that the local density increases gradually, and the clusters are more closely connected withiincreasing.It turns out that there is a significant drop inrpfor Cu–Zr pair when the number of shared atoms increases from 4 to 5.This may be due to the distortion of clusters for the connected Cu–Zr pair.

Figures 4(a)–4(d)show the populations of different connecting structures.It can be found that the 4-, 5-, and 6-number sharing atoms are of large population, indicating the main connecting structure for two nearest neighbors.WithcCuincreasing, the population of 4-number sharing polyhedrons decreases, while those of 5- and 6-number sharing ones increase.Especially, the population of 5-number sharing structure for Cu–Cu pair drastically increases from the maximum about 50%to 67%in the composition range investigated.This would be due to the increase of the icosahedral clusters with the increase ofcCu, which are rich in five-fold symmetry and are known to center around Cu atoms in Cu–Zr metallic glass.[15]

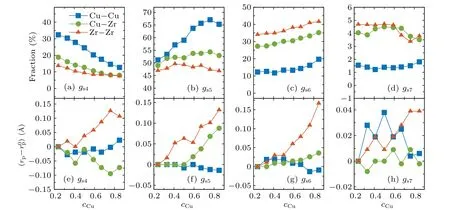
After accomplishing the composition-dependent population, we find that the atomic distance in the structure sharing different numbers also depends on concentration.Figures 4(e)–4(h) display the changes ofrpwithcCu.Interestingly,rpremarkably increases withcCuincreasing in all these connecting structures for Zr–Zr pairs.Expect for the value of Cu–Zr pairs ings5,rpis almost independent of chemical composition.The expansions ofrpfor Zr–Zr,especially in the pentagonal and hexagonal bipyramid structures(for which the populations are the highest), can lead to the increase of the nearest atomic distance,upon mixing Cu atoms.

4.Conclusions

Classic molecular-dynamics simulations performed to investigate the variations of structure of Cu–Zr metallic glass at room temperature with Cu concentration systematically.The glass structure is measured by pair distribution function,which exhibits a concentration-dependent phenomenon for the Zr–Zr nearest atomic distance, in contrast to the hard-spherelike model.This non-entropic mixing effect is also found in the composition-dependent chemical environment,where the connecting propensity of Cu atoms with Zr atoms monotonically increases with Cu addition increasing.The affiliating tendency of the smaller Cu atoms can, somehow, squeeze the bigger neighboring Zr atoms outwards around the central Zr atoms, which is verified by decomposing the connection of the nearest neighbors into four different polyhedral structures,i.e., the quadrilateral, pentagonal, hexagonal, and heptagonal bipyramids.With the increase of common sharing neighbors,the distance from the central atom decreases,indicating more closely packed structure.While the population of hexagonal,and heptagonal bipyramids increases,we find a remarkably increase of the connecting distance for all these local structures.This leads to the expansion of Zr–Zr nearest atomic distance with Cu concentration increasing, and demonstrates that the interplay between chemical interaction and geometrical packing can affect the atomic structure in Cu–Zr metallic glass.

Acknowledgements

The authors thank the High Performance Computing Cluster (HPC) of Central South University for providing the computer resources.

Project supported by the Open Research Fund of Songshan Lake Materials Laboratory, China (Grant No.2022SLABFN14).