Role of excited states in helium-like ions on high-order harmonic generation

Jiang-Hua Luo(罗江华) and Jia-Jun Xiao(肖佳俊)

School of Physics and Optoelectronic Engineering,Yangtze University,Jingzhou 434023,China

Keywords: high-order harmonic generation,ultrafast phenomena,excited states

1.Introduction

High-order harmonic generation (HHG) is well known as a high-nonlinear non-perturbative optical phenomenon produced by interaction of strong laser fields with atoms or molecules.The most direct consequence is to generate coherent light in the extreme ultraviolet and even soft x-ray region,as a very attractive source of attosecond pulses that can make it possible to capture structures and dynamics of targets with spatiotemporal resolution on both the attosecond and angstrom scales.[1–3]The fast developments of HHG have important applications for understanding attosecond electron dynamics and other related ultrafast atomic or molecular physics.[4–13]

An HHG spectrum has a very typical structure.First,the spectral intensity decreases with the increase of harmonic frequency,then remains almost constant starting from the ionization threshold, followed by a plateau region, and finally, the harmonic intensity decreases rapidly after the cutoff energyIp+3.17Up,whereIpis the ionization potential andUpis the ponderomotive energy of the laser field.[14]The HHG process can be well described by the classical three-step model:[15]ionization, acceleration, and recombination.Firstly, when atoms (ions or molecules) encounter a strong laser electric field,their potential barrier is lowered and the electrons in the ground state are ionized by tunneling ionization.Then the ionized electron is accelerated in the electric field and gains kinetic energy.Finally,as the electric field reverses its sign,part of the accelerated electron wavepacket is driven back and recombined with the parent ion,releasing both the kinetic energy and the ionization energy in the form of high-energy photons,known as HHG radiation.

The three-step model well explains the generation of high-energy photons, i.e., the HHG above the ionization threshold.However, it cannot give a clear picture of the radiation mechanism of low-order harmonics below the threshold,because it ignores the influence of the Coulomb potential and the excited states of atoms.Low-order harmonics below or near the threshold are an important means of generating vacuum-ultraviolet combs and have gradually become a hot issue in recent years.[16–18]Generally speaking,the study of harmonic radiation below the ionization threshold is still on the basis of quantum path interference theory,combined with the influence of Coulomb potential.Additionally, excited states have been found to play an important role in the generation of lower-order harmonics.[19,20]Under the action of strong fields,electrons in the ground state may be excited at the same time as ionization.This process can selectively increase the efficiency of certain low-order harmonics, and a resonance excitation peak corresponding to excited state energy will appear in the harmonic spectrum.For helium-like ions, such as helium atoms,lithium cations,and beryllium dication,due to the high ionization energy, the ionization rate of the electrons is very low,and their HHG efficiency can be expected to be low as well.

In this paper, we use the time-dependent Hartree–Fock (TDHF) method to solve the three-dimensional timedependent Schr¨odinger equation (TDSE) and calculate the HHG spectrum of helium-like ions.The results show that the intensity of HHG increases obviously from a certain order harmonics with fixed energy below the threshold.This is quite different from the resonance excitation peaks studied before.[19]By our calculation, the harmonic spectrum starts from the point where enhancement occurs and the intensity of its subsequent orders all increases substantially.Moreover,the results also show that the location where the enhancement occurs is independent of the laser intensity as well as the wavelength.To reveal the inner physics, we propose a “four-step model” mechanism: (i) The ground-state electrons are resonantly excited or virtually excited to an excited state by a multiphoton process.(ii) The electrons in the excited states are further ionized.(iii) The ionized electrons are accelerated in laser fields.(iv) Parts of the accelerated electrons coincide with the parent ion and radiate harmonics.Since the ionization energy of the excited state is lower than that of the ground state,the ionization rate of the excited state electron is greatly improved.As a result, the intensity of the harmonics higher than the ionization energy of the excited state is significantly enhanced.Such a four-step model mechanism can reasonably explain the resonance excitation peak of helium-like ions and also makes for richer dynamics of harmonic enhancement.

2.Numerical methods

HHG from helium-like ions subjected to a linearly polarized laser field is investigated by using the TDHF method following the approach developed by Zhanget al.[21]The DMTDHF package is employed for the simulations.This package is originally developed for diatomic molecules in prolate spheroidal coordinates.Here, we have made modifications such that it can be used for atoms with spherical symmetry.The central idea is that we can set the nuclear charge of one nucleus of the diatomic molecule to zero and mimic a spherical symmetric atom.The interaction between the laser field and the target is described by the TDSE

whereH0is the laser-free multielectron operator andVl(t)the laser interaction part.The laser interaction termVl(t)reads

whereriis spatial coordinate of thei-th electron andE(t)is the electric field of the laser pulse,

Here,ω=2π/Tis the angular frequency,N0is the total number of the laser optical cycles, andE0is the amplitude of the electric field.Based on the TDHF ansatz, the wave function,solution of the time-dependent Schr¨odinger equation(1),is approximated by an antisymmetrized product of time-dependent single-electron wave functions.The equations for these singleelectron wave functions, i.e., the so-called TDHF equations,are numerically solved by employing a computational procedure based on a finite-element discrete-variable representation(FE-DVR) in prolate spheroidal coordinates.The time propagation is accomplished using a short iterative Lanczos(SIL)method.HHG spectra are computed as the squared modulus of the Fourier-transformed electric dipole acceleration,which is obtained by the second derivative of the dipole moment,

whereσis the width of the Gaussian time window in the Gabor transform.

3.Results and discussions

Fig.1.High harmonic spectra for(a)helium atom, (b)lithium cation,and(c)beryllium dication.The laser field is linearly polarized along the z axis at wavelength of 800 nm,with intensity of 5.0×1014 W/cm2 and total pulse duration of 10 optical cycles.The arrow in each panel indicates the position where the enhancement of harmonic intensity starts.

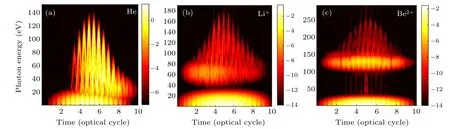
Fig.2.Time-frequency maps for(a)helium atom,(b)lithium cation,and(c)beryllium dication.Laser parameters are the same as those in Fig.1.

Figures 1(a)–1(c) present the HHG spectra of a helium atom, lithium cation, and beryllium dication, respectively.In the calculations, the intensity of the driving laser pulse is set to 5.0×1014W/cm2,the wavelength to 800 nm,and the total pulse duration to 10 optical cycles.The ionization energies of the ground state of the three systems on Hartree–Fock level are 24.9788 eV,75.9841 eV,and 154.2101 eV,respectively.Under these conditions,the Keldysh parameter of helium-like ions is much less than 1, so it is in the tunneling ionization region.As can be seen in Fig.1,the harmonic spectra of helium-like ions show a very typical structure.First, the HHG intensity decreases rapidly with the increase of frequency.Then,initial from 22 eV for the helium atom,62 eV for the lithium cation and 124 eV for the beryllium dication,the spectral intensities appear to be significantly enhanced and the magnitude of the enhancement is about 5–6 orders.Lastly,the harmonic intensity remains basically unchanged after a slight decrease and presents a plateau structure before the cutoff energy.It is worth noting that the energy corresponding to the initial position of harmonic enhancement is less than the ionization energy of the corresponding atom(ion).

To investigate the detailed structure of the harmonic enhancement in Figs.1(a)–1(c), the time-frequency maps[22]of the HHG spectra are given in Figs.2(a)–2(c),respectively.For the helium atom,as shown in Fig.2(a),the position of the enhancement around 22 eV is not obvious,while a concave structure can still be seen in the time-frequency distribution below 22 eV, indicating that the harmonic intensity increases from 22 eV.For lithium cation and beryllium dication, visible resonance enhancement peaks appear near 62 eV and 124 eV in Figs.2(b)and 2(c),respectively.In Figs.2(b)and 2(c),the intensities of the harmonics below 62 eV and 124 eV are clearly lower.These time-frequency features are consistent with the harmonic spectrum structures in Fig.1.

In the following, we investigate the effect of the driving laser parameters on the positions of the harmonic enhancement.We first calculate the harmonic spectra of helium atom with various driving intensities and wavelengths.The results are shown in Fig.3.For the same laser wavelength of 800 nm,Fig.3(a)exhibits the harmonic spectra with driving intensities of 2.0×1014W/cm2, 3.0×1014W/cm2, 4.0×1014W/cm2,and 5.0×1014W/cm2,respectively.For the same driving intensity of 3.0×1014W/cm2, Fig.3(b) exhibits the harmonic spectra with laser wavelengths of 800 nm,900 nm,1000 nm,and 1100 nm, respectively.Despite the difference in spectral profile, these HHG spectra show the common enhanced position, around 22 eV, as shown in Fig.3 with a vertical dashed line.For comparison with Fig.1 more clearly, we then calculate the harmonic spectra of helium atom, lithium cation, and beryllium dication at other driving parameters.Figures 4(a)–4(c)show the corresponding HHG spectra from the three ions driven by a mid-infrared laser with the intensity of 8.0×1014W/cm2,wavelength of 1200 nm,and total pulse duration of 10 optical cycles.It can be seen that the harmonic spectrum driven by the mid-infrared laser in Fig.4 is similar to those in Fig.1.Moreover,in Figs.1 and 4,the intensity starts to increase at a same harmonic order below the threshold,corresponding to about 22 eV of the helium atom, 62 eV of the lithium cation,and 124 eV of the beryllium dication.For the beryllium dication, because of the extremely large ionization energy,the ionization probability is very small.As a result,the intensity of the harmonics is very low and almost has the same level of background noise.The cutoff of the plateau can not be well resolved.Nevertheless,the peak of the enhancement can be clearly observed.We expect that the harmonic spectrum can be well resolved using a laser pulse with higher intensity,which is out of our computational capability.Additionally,the enhancement position of the same ion does not alter with the change of driving laser parameters.These imply that the initial position of enhancement is determined by the ion itself,i.e.,the ion potential function and the properties of the excited state,and has nothing to do with the parameters of the driving laser.

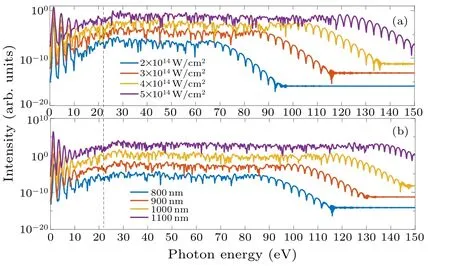
Fig.3.(a)HHG spectra for helium with different laser intensities.The wavelength is set to 800 nm.(b)HHG spectra for helium with different laser wavelengths.The intensity is set to 3.0×1014 W/cm2.The vertical dashed line shows the position where the enhancement of harmonic intensity starts.

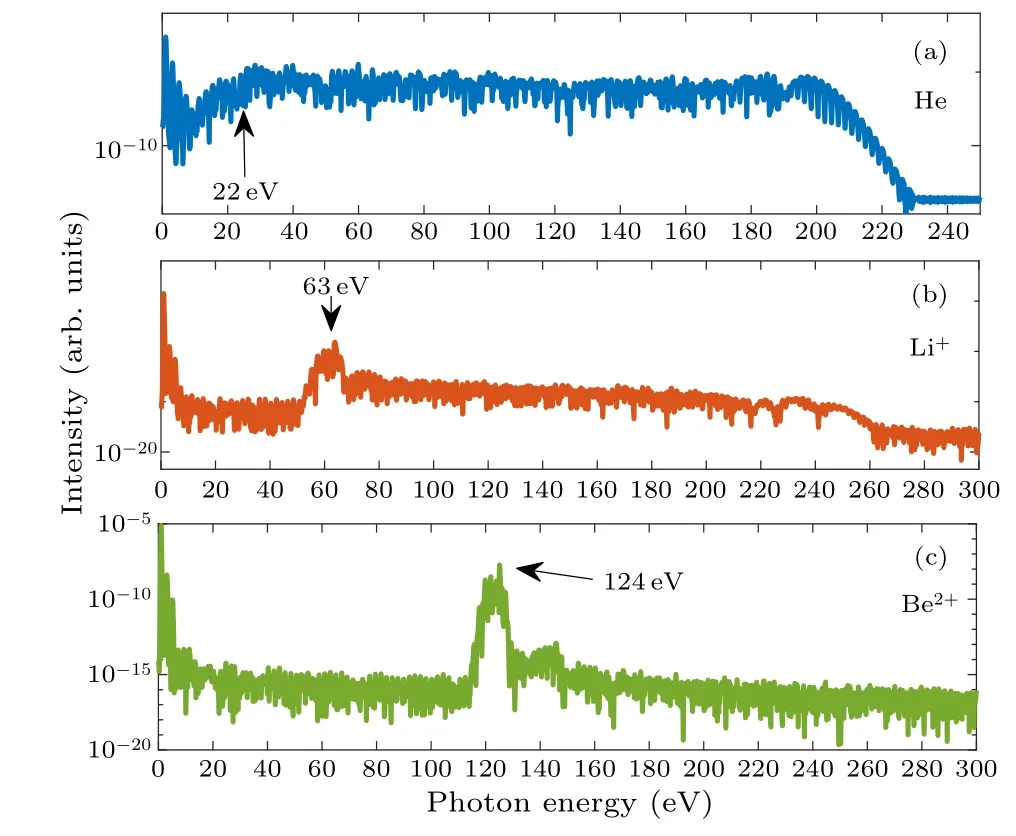
Fig.4.The same as Fig.1 but for laser at wavelength 1200 nm in intensity of 8.0×1014 W/cm2 with total pulse duration of 10 optical cycles.

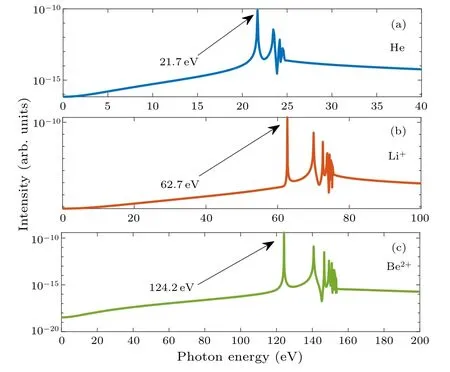
Fig.5.Linear excitation spectra for (a) helium atom, (b) lithium cation, and (c) beryllium dication.A delta pulse with an intensity of 2.0×1012 W/cm2 is adopted.

To analyze the relationship between the harmonic enhancement effect and the excited states of ions, we calculate the linear excitation spectra of the three targets.The linear excitation spectrum is obtained by first calculating the dipole moment of the electron through short pulse excitation in the form of the delta function, and then taking the Fourier transform of the dipole moment.Figure 5 presents the linear excitation spectra of helium-like ions, where the driving laser parameters are the same as those in Fig.1.As can be seen from Fig.5,the first peak of the linear excitation spectrum corresponds to the multi-photon excitation transition of an electron from 1s2to 1s2p, and the peak positions of the three ions are located at 21.7 eV, 62.7 eV, and 124.2 eV, respectively.These energies are slightly different from the NIST data 21.2 eV,61.3 eV,and 121.9 eV.This is due to the meanfield approximation used in our TDHF model, which can not reproduce the fully correlated excited state energies.Combined with the HHG of Fig.1, it can be found that the initial position of resonance enhancement of harmonic spectrum is consistent with the position of multi-photon excitation transition from 1s2to 1s2p in the linear excitation spectrum.Obviously,the excitation transition of the electron is involved in the HHG process and has an important influence on the intensity of harmonics.[20]It should be noted that, unlike the previous work,[19]our results show that the excitation transition enhances the harmonic intensities of all orders after the resonance energy of 1s2to 1s2p,i.e.,the intensity of the harmonics above the enhancement peak is in orders of magnitude higher than those below the peak.This phenomenon is rarely studied before.

Fig.6.Ionization probability of helium atom calculated by TDHF(blue curve)and ADK(red curve).Laser parameters are the same as those in Fig.1.

Finally,we calculate the time-dependent ionization probability of the He atom to further analyze the specific role of electron excitation in the HHG process.In the calculation,the laser parameters are the same as those in Fig.1.Figure 6 shows the ionization rate in terms of the TDHF method,which considers the ionization of ground and excited state electrons.The traditional ADK ionization rate[23]of the ground state is also plotted in Fig.6 for comparison.We figure out that the ionization rate by the TDHF method is higher than that of ADK.Under the laser conditions of our calculation, most of the electron wave packets are in the ground state but not ionized owing to the high ionization energy of the system.According to the strong field approximation model,the harmonic efficiency is proportional to the electron ionization probability.It is inferred that the harmonic enhancement effect is due to the increase in the ionization rate of the system,i.e., the contribution of the excited state electrons.Similar to the threestep model, we hereby propose a four-step model for HHG of helium-like ions: under the action of the driving field, the electrons in the ground state 1s2is excited to the state of 1s2p by a multi-photon transition;subsequently,the electron in the excited state 1s2p is ionized by laser field; the ionized electron then accelerates in the laser field and finally recombine,radiating HHG.In this process, the ionization probability increases because the ionization energy of the excited state is lower than that of the ground state.Therefore, the intensity of those harmonics with energies above the excitation energy of 1s2to 1s2p is significantly enhanced because of the higher ionization probability.

4.Conclusions

In summary, we have used the time-dependent Hartree–Fock method to systematically investigate the enhancement effect of HHG in helium-like ions.It is shown that HHG intensity increases significantly from a certain order harmonics with energy below the ionization threshold.In addition, the initial location of this enhancement is independent of the intensity and wavelength of the driving laser field.Further analysis shows that the excitation transition enhances the harmonic intensities of all orders after the resonance energy of 1s2to 1s2p, and consequently the intensity of the harmonics above the enhancement peak is orders of magnitude higher than those below the peak.The reionization mechanism of electron excitation is discussed and a four-step model is proposed to describe the physical process of harmonic enhancement.This study can provide theoretical guidance for generation of vacuum UV frequency combs by subthreshold harmonics.

Acknowledgment

Project supported by the National Natural Science Foundation of China(Grant Nos.12274294 and 12075036).