A zeroing neurodynamics‐based location method for nodes in underwater acoustic sensor network

Shuqiao Wang| Xiujuan Du,2 | Tiantai Deng

1College of Computer,Qinghai Provincial Key Laboratory of loT, Qinghai Normal University,Xining, China

2The State Key Laboratory of Tibetan Intelligent Information Processing and Application, Xining,China

3The Department of Electronics and Electrical Engineering, The University of Sheffield,Sheffield,England, United Kingdom

Abstract Zeroing neurodynamics methodology, which dedicates to finding equilibrium points of equations,has been proven to be a powerful tool in the online solving of problems with considerable complexity.In this paper,a method for underwater acoustic sensor network(UASN) localisation is proposed based on zeroing neurodynamics methodology to preferably locate moving underwater nodes.A zeroing neurodynamics model specifically designed for UASN localisation is constructed with rigorous theoretical analyses of its effectiveness.The proposed zeroing neurodynamics model is compatible with some localisation algorithms, which can be utilised to eliminate error in non-ideal situations,thus further improving its effectiveness.Finally,the effectiveness and compatibility of the proposed zeroing neurodynamics model are substantiated by examples and computer simulations.

K E Y W O R D S artificial neural network, internet of things, underwater acoustic sensor network

1 | INTRODUCTION

In recent decades, approaches based on neural networks are often exploited to meet the increasing demand of powerful computing methods and are proven to be effective tools in solving computational problems [1–3].Particularly, zeroing neural network (ZNN), which transforms various computing problems into zero-finding problems,is developed to conduct online operations for solving time-varying problems, and is employed in optimisation [4], robot motion control [5, 6],mobile manipulators [7, 8], and a variety of complicated computational problems[9–12].ZNN models are constructed based on a special design formula, whose main role is to find the equilibrium points of equations by driving specifically designed error functions to zero.Zeroing neurodynamics,which is further generalised from ZNN design methodology,is considered a systematic neurodynamics approach for timevarying problem solving [13].In ref.[14], static tensor-based problems are solved via approaches based on zeroing neurodynamics methodology.As a further improvement, several finite-time convergent zeroing neurodynamics models for solving time-varying tensor-based equations are presented in ref.[15].In ref.[16], an improved type of zeroing neurodynamics model that dedicates to solving generalised Sylvester equations is presented, which finds applications in robots and acoustic source localisation.An optimisation approach for deep neural network first-order optimisers is presented based on zeroing neurodynamics in ref.[17].As an important component of the zeroing neurodynamics model, activation functions are verified to be capable of greatly accelerating convergence speed, and thus draw much attention from researchers.Notably, several different activation functions are developed and applied to zeroing neurodynamics models such that the resulting models are finite-time convergent [18, 19].The finite-time convergence property is also further investigated in their work with thorough theoretical analyses [20].

Research on underwater acoustic sensor network (UASN)has attracted increasing concern in recent years.Being viewed as a key technology of UASN, underwater localisation inherits the basic methodology of wireless sensor network (WSN)localisation [21].Due to the fact that radio signals can only travel a short distance underwater, UASN relies on acoustic signals for long-range transmission.Consequently, UASN is challenged by difficulties introduced by complicated underwater environments,such as limited bandwidth,limited energy,long propagation latency, low link quality, and more [22].As such,a variety of UASN localisation algorithms are designed to accustom the underwater environments [23, 24].In ref.[25],several modified time difference of arrival (TDoA) algorithms are presented for nodes to locate themselves passively with low energy consumption.A node localisation algorithm that utilises node movement prediction is developed in ref.[26]to improve localisation accuracy on moving nodes.By using a number of synchronised mono-static sensors in motion, a method of locating a moving underwater object is investigated in ref.[27].In ref.[28],in order to improve anchor node locating accuracy,a frequency-based anchor node localisation and prediction algorithm is designed.In general, the research of UASN localisation focuses on locating moving nodes with high precision,high robustness and limited expense.

The main purpose of this paper, which is motivated by problems encountered during the development of UASN routing protocols, is to propose a zeroing neurodynamics model with activation functions that are suitable for continuous UASN localisation.Precisely locating underwater nodes often needs measuring the distances between nodes or the angles of incoming transmission, which requires extra devices to be equipped on underwater nodes.However, this may exhaust the limited energy reserves of underwater nodes and potentially be very expansive.Furthermore,due to the low data rate, it is appropriate to transmit only the most important information that maintains the connectivity of a network,which leads to the development of many non-location-based routing protocols.However, the position information of nodes can prove invaluable for a network to establish connections, and the data transmission routes can be decided easier if the position information of nodes is ready and available.Thus, it is necessary to develop a method of node localisation for UASN with limited expanse.As the energy costs are dominated by transmission in UASN[21],the zeroing neurodynamics model proposed in this paper focuses on providing nodes position information continuously without increasing data exchanges between nodes,in other words,trading computational costs for transmission costs.Combined with other positioning strategies,the accuracy of the proposed model is revealed to be improvable.

The remainder of this paper is organised into five sections.The problem formulation is presented in Section 2 with details of several basic UASN localisation algorithms.The construction methodology of the zeroing neurodynamics model for UASN localisation is proposed in Section 3 along with activation functions.As a continuation, vigorous theoretical analyses on the proposed zeroing dynamics model are provided in Section 4.The effectiveness of the newly proposed zeroing neurodynamics model is substantiated by illustrative computer simulations conducted as examples in Section 5.Finally,in Section 6,this paper is concluded with final remarks.Before ending this introduction,the main contributions of this paper are listed below:

1) A zeroing neurodynamics model is specifically designed for UASN localisation, which provides an alternative method to effectively locate a moving underwater node.The proposed model is capable of quickly locating a underwater node with fast convergence speed.If the data used in calculations is not already contaminated by error, then the unknown moving node can be locate with the zeroing neurodynamics model with high precision.In addition, the model can adapt different activation functions to further enhance its convergence speed.Theoretical analyses prove that it has finite-time convergence property if certain activation functions are applied.

2) The proposed zeroing neurodynamics model is designed to be compatible with other components of localisation strategies used in UASN.By combining with other errorreducing methods, the effectiveness of locating the moving underwater node can be further improved in the face of inaccurate data, which is demonstrated in examples.

2 | PROBLEM FORMULATION

In general, the existing UASN localisation algorithms inherit the basis of WSN localisation and are often divided into rangebased algorithms and range-free algorithms.The range-based algorithms require actually measuring the distance or angle between nodes, while the range-free algorithms approximate the distance between nodes based on connectivity information.Considering the distributed nature of UASN, it is appropriate to allow each node to locate itself individually.In distributed localisation,both kinds of algorithms require a node to gather information about other nodes first in order to calculate its own position, and thus a large portion of the localisation procedure is similar.In addition, depth information can be obtained by measuring water pressure in UASN.Therefore,the localisation in this paper focuses on two-dimensional (2D)situations, as three-dimensional problems can be transformed into 2D ones if depth information is already known.

The basic DV-hop algorithm uses hop counts and estimated distance per hop to locate target nodes.Let anchor nodes denote the nodes which are aware of their own positions,and unknown nodes denote the nodes that need to locate themselves.The localisation procedure of 2D basic DV-hop can be organised into three steps as follows:

• Each anchor node broadcasts a packet that contains its own position into the network, with the initial hop counts value being set as 1.A table containing the locations of anchor nodes and minimum numbers of hops is maintained by each node.If a packet from a particular anchor node is received while the hop counts value is lower than the current one in the table,then the table is updated.Otherwise,the packet is discarded.If the table is successfully updated, then the packet is forwarded by the node and the hop counts value is increased by 1.In this way, the positions of anchor nodes and corresponding minimum hop counts are flooded in the network.

• The next step is to approximate the average distance per hop of each anchor node.For an anchor node with coordinates (xi,yi), the average distance per hopσican be approximated as follows:

where(xj,yj)denotes the coordinates of anchor nodej,nis the total number of the anchor nodes, andhijdenotes the hop counts between nodeiand nodej.After the average distance per hop is approximated, the message is flooded into the network in a similar manner.

• The final step is calculating the position of nodes.When an unknown node is aware of the approximated distance towards at least three anchor nodes, its own coordinates can be calculated via the multilateration method.Let (x,y)denote the coordinates of an unknown nodeX,which is to be located,(xi,yi)denote the coordinates of a set of anchor nodes Ni, wherei= 1, 2, …,n.Letkibe the hop counts between theith anchor node and unknown nodeX, the distance between these two nodes can be approximated asdi=ki×σi.After that, the coordinates (x,y) can be calculated by

By subtracting the last equation with previousn- 1 equations, the above Equation (2) is rewritten intoAx=bform, which can be detailed as follows:

where coefficient matrixA∈R(n-1)×2,vectorb∈R(n-1),andxis the coordinate to be calculated.Note that the above equation is often overdetermined and the coordinate of the unknown node is commonly obtained via the least square method.

It is worth mentioning that the above basic DV-hop algorithm is a range-free localisation algorithm because the distance between nodes is approximated.However, if the distance is actually measured, such as measuring the arrival time of packets, then the algorithm becomes range-based and is basically consistent with the time of arrival (ToA) algorithm.

Similarly, the angle of arrival (AoA) localisation algorithm,as another kind of range-based algorithm, locates unknown nodes by measuring arrival angles between unknown nodes and anchor nodes.After the arrival angles from several anchor nodes to an unknown node are obtained,the coordinate of the unknown can be calculated.The mathematical expression of the 2D AoA algorithm can also be written inAx=bform:

whereαiis the arrival angle ofith anchor node and tan(αi) = (y-yi)/(x-xi).

The TDoA algorithm is another popular range-based localisation algorithm.Its principle is to calculate the coordinate of a source node by comparing the TDoA at different receiver nodes,where the source node is an unknown node and the receiver nodes are often anchor nodes.The mathematical expression of 2D TDoA algorithm follows a similar pattern and is written inAx=bform:

whereki=x2i+y2i,rirepresents the distance betweenith anchor node and the unknown node, andrijthe distance difference betweenriandrj.The TDoA algorithm shares many similarities with the ToA algorithm.However, the TDoA algorithm doesn't require the system clocks of nodes to be synchronised.

Apparently, despite utilising different methods to locate unknown nodes,these localisation algorithms involve solving a matrix equation in the form ofAx=b, which is essential to obtain the coordinates of unknown nodes.It is also worth mentioning that the matrix equations in these localisation algorithms are static because of the scenario they are designed for.However, as UASN differs from WSN in various ways,necessary improvements should be made in order to obtain better performance.

3 | ZEROING NEURODYNAMICS MODEL FOR UASN LOCALISATION

This section focus on laying the framework of a zeroing neurodynamics-based localisation method that is suitable for an unknown node to locate itself dynamically in UASN.Thus,the problem to be solved is considered a dynamic one in this section.The static instances are theoretically special cases of dynamic problems and are covered in discussions.

Assume that an unknown node is always aware of the coordinates of anchor nodes in the corresponding network.The original static problem can be transformed into

in which every element inA(t)andb(t)is dependent on timet,the solution to be obtained is denoted byx(t), andTdenotes the transpose operation of vectors or matrices.Based on the above Equation (6), an error monitor function is defined as

Apparently, given thatɛ(t) = 0, then the theoretical solutionx*(t)is an equilibrium point of Equation(6).Hence from a control perspective, the object is to regulate the error monitor functionɛ(t) to zero, so that the state vectorx(t)reaches theoretical solutionx*(t).Based on zeroing neurodynamics design methodology, a basic design formula as follows can be used to regulateɛ(t):

in which scaling factorβ>0, ˙ε(t)represents the time derivative ofɛ(t),and Ψ(⋅):Rn→Rnis a vector-valued activation function array, of which each element is activation functionψ(⋅).Substituting Equation(7)into Equation(8)yields

The above equation is the zeroing neurodynamics model designed for finding the solutionx*(t) of Equation(6),and in turn, locating the unknown node.If the matrixAT(t)A(t) is non-singular at any time, then the above zeroing neurodynamics model (9) can be rewritten as

Theoretically,zeroing neurodynamics models can adopt any monotonically-increasing odd functions as activation functions.Certain activationfunctionsare capable of enhancing the zeroing neurodynamics model with various properties.A few special examples are listed below[20]:

1) Linear activation function:ψ(ɛ) =ɛ.

2) Power-Q activation function:

3) Bi-Power activation function:

In above activation functions,ais a positive scaling factor and the function sigϑ(ɛ) is detailed as follows:

where|⋅| means absolute value.Both the Power-Q activation function and the Bi-Power activation function can accelerate the convergence speed of zeroing neurodynamics model (10).With appropriate activation functions applied, the zeroing neurodynamics model that is suitable to locate unknown nodes in UASN can be constructed following the steps detailed in this sector.

4 | CONVERGENCE ANALYSES

In this section, theoretical analyses on the convergence property of the proposed models are given below.

Theorem 1If AT(t)A(t)is non-singular and a monotonicallyincreasing odd activation function is applied,then starting from any initial state x(0),the zeroing neurodynamics model(10)globally converges to the theoretical solution x*(t)of problem(6).

Since Ψ(⋅) is monotonically-increasing odd, ˙L(t)≤0 and ˙L(t)=0 only ifɛ(t) = 0.In addition, due to its definition,apparentlyL(t) ≥0 andL(t) = 0 only ifɛ(t) = 0.In other words, ˙L(t)<0,L(t)>0 forx(t) ≠x*(t), ˙L(t)=0,L(t)=0 only whenx(t) =x*(t).Based on Lyapunov stability theory, it is concluded that the zeroing neurodynamics model (10)converges to the theoretical solutionx*(t) with time.□

Theorem 2If AT(t)A(t)is non-singular and the Bi-Power activation function is applied,then starting from any initial state x(0),the zeroing neurodynamics model(10)globally converges to the theoretical solution x*(t)of problem(6)with finite-time convergence.

ProofConsider the equation ˙ε(t)=-βΨ(ε(t)), that is, the compact form of the zeroing neurodynamics model(9).Itsith subsystem is expressed as

whereγ=aβand the time derivative ofξ(t) is represented by ˙ξ(t).Sinceγξq(t) in the above equation is non-negative, an equation can be obtained as follows:

• The situation ofξ(0) > 0.According to Equations (3) and(8), the dynamics ofξ(t) can be expressed as follows:

By summarising all three situations, the conclusion is that the zeroing neurodynamics model (10) with the Bi-power activation function converges in finite time.□

5 | ILLUSTRATIVE EXAMPLES

Several computer simulations are conducted to verify the effectiveness of the proposed models in this section.The advantages of the model proposed in this paper are also discussed accordingly.

5.1 | Example 1

Consider a square area with a side length of 1000 m, in which five anchor nodes are randomly deployed following the uniform distribution.Assume that all nodes are stationary and distance measurements are accurate.Then an unknown node can calculate its own position accurately via zeroing neurodynamics model (11) if it has position information of anchor nodes under this ideal configuration.The initial statex(0)is set as the coordinates of the closest anchor node.

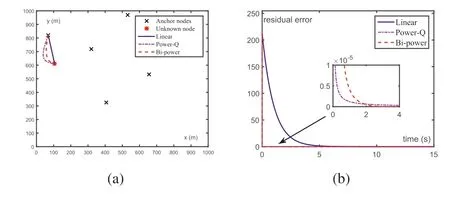
F I G U R E 1 A randomly deployed unknown node locates itself via the zeroing neurodynamics model (11), with the Linear activation function(signified by Linear), the Power-Q activation function (signified by Power-Q), and the Bi-power activation function (signified by Bi-power), where q = 2 for Power-Q activation function and p = 0.5, q = 1.5 for Bi-power activation function.(a) Trajectories of x(t).(b) Residual error ‖ɛ(t)‖2.

The simulation result is plotted in Figure 1.Apparently, as observed from Figure 1a, the zeroing neurodynamics model(11)is capable of converging to the theoretical solution,which means the unknown node is located.With different activation functions applied, the convergence ofx(t) follows different trajectories as well.The residual error ‖ɛ(t)‖2during the convergence of zeroing neurodynamics model (11) with three activation functions presented in this paper is displayed respectively in Figure 1b.Compared to the Linear activation function, it is evident that both the Power-Q activation function and the Bi-power activation function are capable of greatly accelerating the convergence.It is worth noting that different values ofqare assigned to the Power-Q activation function and the Bi-power activation function.In general, a largerqmeans faster convergence speed.However, as can be observed in Figure 1b, after around 2 s, the zeroing neurodynamics model(11)with the Bi-power activation function has a smaller‖ɛ(t)‖2than the rests,which is because of the finite-time convergence property and is consistent with theoretical analyses in Section 4.

5.2 | Example 2

In this example, scenario configuration is largely the same as the previous example, except that nodes are considered dynamic instead of stationary.An unknown node that is to be located is set to be cruising around a random point in a circle within the test area.Thus,the localisation problem is dynamic if the node locates itself continuously.

To the best of authors' knowledge, there are few existing neurodynamics-based UASN localisation methods, while conventional UASN methods tend to track node positions via solving a series of static equations.Thus, for comparison purpose,another type of neurodynamics model is constructed following the classic gradient neural network (GNN) methodology.The model is detailed as follows:

where scaling factorδ> 0, and Ψ(⋅) is a vector-valued activation function array withψ(⋅) being tanh activation function.The GNN model(12)is able to precisely find the least square solution of the original static localisation problem.However,in face of dynamic scenarios it has some limitations.As such,the addition of tanh activation function is to suppress chattering and yield better results.

F I G U R E 2 Localisation of a cruising unknown node via the zeroing neurodynamics model (10) (signified by ZD), and the GNN model (12)(signified by GNN), with theoretical trajectories of the unknown node added for comparison (signified by Theoretical).(a) Trajectories of x(t).(b) Residual error ‖ɛ(t)‖2.GNN, gradient neural network; ZD, zeroing neurodynamics.

As can be observed from Figure 2a,the movement path of the unknown node is covered by the trajectories of the state vectorx(t) of the zeroing neurodynamics model (10).In addition,Figure 2b demonstrates that as time goes on,‖ɛ(t)‖2of the zeroing neurodynamics model (10) converges to zero,that is, the state vectorx(t) converges towards the position of the unknown node.Thus, despite that the unknown node is moving,the zeroing neurodynamics model(10)can effectively track and locate the unknown node.In contrast, it is visually demonstrated that the GNN model(12)can not precisely track the position of the unknown node in this case.Furthermore,as shown in Figure 2b, ‖ɛ(t)‖2of the GNN model (12) is not successfully reduced to zero, which means a large portion of error always exists.By comparing the performances of these two models, it can be concluded that the zeroing neurodynamics model proposed in this paper is much more effective in this case.Note that zeroing neurodynamics model(10)with the Power-Q activation function or Bi-power activation is able to locate to moving unknown node as well, and converges faster,which is similar to that of Figure 1b,but is not shown in Figure 2 for simplification.

5.3 | Example 3

Consider an autonomous underwater vehicle (AUV), whose starting point is set as the coordinate origin(0,0),moving along the positive direction of thex-axis at an average speed of 2 m/s.There are eight buoys serving as anchor nodes within a 1000 m radius centred around the AUV, which are considered to be within effective communication range.All nodes,including the AUV, are under the effects of elements such as water waves,and begin to drift away from the planned positions as time goes on.To locate the moving AUV, the measurement error of distance between nodes is neglected andx(0)is set to be(0,y0),wherey0∈[-10,10].Both the zeroing neurodynamics model(10) and the GNN model (12) are tested in this example.

Figure 3 illustrates the simulation result.Careful examination shows that the zeroing neurodynamics model(10)with all three kinds of activation functions converges to the theoretical solution, and thus the movement trajectory of the AUV is successfully and effectively tracked.It can be further observed from Figure 3 that the zeroing neurodynamics model(10)with the Power-Q activation function or the Bi-power activation function is capable of quickly locating the AUV near its starting point.The trajectories of the zeroing neurodynamics model(10) with these two activation functions overlap with each other, as their effects are highly identical.It is noticeable that,unlike in Example 2, the position of the moving AUV is successfully tracked by the GNN model(12)in this case.This is largely because the time derivative ofA(t) is overall much smaller than that of the previous one.As shown in Figure 3,after careful adjustment of parameters, it is possible to reduce residual error to a negligible amount.However, this can be inconvenient and potentially unreliable in comparison with the zeroing neurodynamics model (10).

5.4 | Example 4

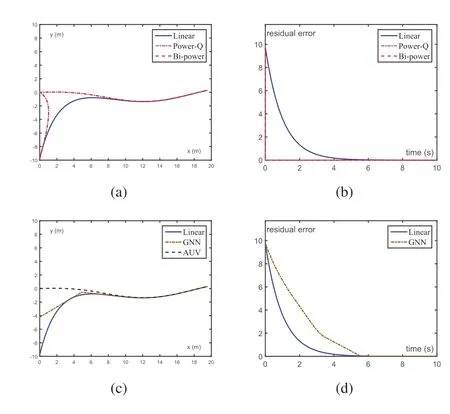
F I G U R E 3 Localisation of a moving AUV via the zeroing neurodynamics model(10),with the Linear activation function(signified by Linear), the Power-Q activation function (signified by Power-Q), and the Bi-power activation function(signified by Bi-power),where p=0.5,q=2.Test result of the GNN model (12) (signified by GNN) and the actual movement trajectory of AUV (signified by AUV) are added for further comparison.(a) Trajectories of x(t).(b) Residual error ‖ɛ(t)‖2.(c) Comparison of x(t).(d) Comparison of ‖ɛ(t)‖2.AUV, autonomous underwater vehicle; GNN, gradient neural network.

In previous examples, it is assumed that the target node to be located always knows exactly the positions of anchor nodes as well as the distances in between.However, in practice,packets are used to exchange data between nodes, which are transmitted periodically rather than continuously.In this example, on the basis of Example 3, the AUV knows the localisation information from all anchor nodes att= 0, but later it can only update the position and distance information of an anchor node upon receiving a packet from that specific anchor node.LetxAUV(t) denote the actual position of the AUV, and the time interval between receiving packets from a specific anchor node follow the exponent distribution with average time intervalte= 5 s.To counter the error caused by outdated information, the localisation is improved by allowing the AUV to predict its current position with its previous position and speed, as well as weighting outdated information less as time goes on.The weighting matrix consist of diagonal elements within [0,1] range.Both the prediction and weighting are made continuously andx(0) = (0,y0), wherey0∈[-100, -50] ∪[50, 100].

It should be noted that in Figure 4,the errore(t)means the distance from the actual coordinatesxAUV(t)of the AUV tox(t).It can be observed from Figure 4 that although the zeroing neurodynamics model(10)is able to reduce‖ɛ(t)‖2to 0,which is verified by previous examples, it can not locate the AUV with similar precision.At roughlyt=2 s,e(t)begins to increase because of the outdated data, then decreases when a new packet is received so that position information is updated.After aroundt= 10 s,e(t) gradually becomes stable and maintains at a relatively small number.The reason for this result is not computational but rather the measurement error introduced into matrixA(t) and vectorb(t) by the outdated data,which is not to be handled by the zeroing neurodynamics model(10)alone without any data preprocessing.As such,it is also demonstrated in Figure 4 that by combining with prediction and weighting strategy, the zeroing neurodynamics model(10)can yield better results,which reduces error roughly by half and has a trajectory much closer to that of the AUV.Note that the prediction and weighting strategy used in this example is preliminary and demonstrative, and further improvement is possible.

5.5 | Example 5

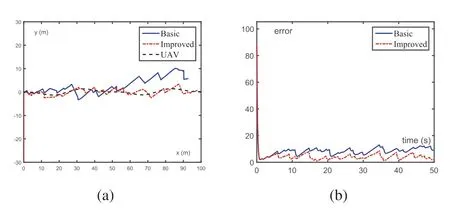
F I G U R E 4 Localisation of a moving AUV based on outdated data via the zeroing neurodynamics model (10), without counter error measure(signified by Basic), and with counter error measure (signified by Improved),where β=5.The actual movement trajectory of AUV is added for comparison (signified by AUV).(a) Trajectories of x(t).(b) Error e(t) = ‖x(t) - xAUV(t)‖2.AUV, autonomous underwater vehicle.

F I G U R E 5 Localisation of a moving AUV based on inaccurate and outdated data via the zeroing neurodynamics model (10), without counter error measure (signified by Basic), and with counter error measure(signified by Improved), where β = 5.The actual movement trajectory of AUV is added for comparison (signified by AUV).(a) Trajectories of x(t).(b) Error e(t).AUV, autonomous underwater vehicle.

In practice, it is unlikely that the distance or angle measurement is completely accurate.As most distance or angle is measured in complicated environments or just roughly estimated in practical UASN, distances measured between nodes are calculated with the error within a ±5% range in this example.All other settings are the same as those in Example 4.Note that as anchor nodes can be as far as 1000 m away, the error can be 50 m large at most, which should greatly disrupt the accuracy of the localisation.

Figure 5 shows the corresponding simulation result.By carefully observing the figure, it is not difficult to notice that the basic zeroing neurodynamics model (10) without counter error measure is able to achieve better results at some time points, for example, at aroundt= 15 s.This is because the error from inaccurate measurement may compensate for that from outdated data, depending on the relative positions of AUV and anchor nodes.In the improved zeroing neurodynamics model (10) with counter error measure, however,such inaccurate distance or angle measurements are discarded due to low reliability,which results in the worse performance at those special time points.Despite that the improved version of the zeroing neurodynamics model (10) is still capable of providing more accurate node positions than the basic one in general, the localisation is greatly disrupted, as can be viewed from Figure 5a, due to a large amount of error introduced by inaccurate measurements.By comparing with the result from Example 4,it is apparent that the proposed model is still quite vulnerable to measurement errors contained in raw data.At current stage zeroing neurodynamics model (10) lacks its own error countering design,its error countering efficiency is highly dependent on what error reducing algorithms are combined with it.Therefore, more advanced error reducing algorithms should be combined with the proposed model to better eliminate such effect.

5.6 | Example 6

To better demonstrate the performance of the proposed zeroing neurodynamics model (10), in this example, comparisons are made between three situations where the average time intervaltebetween receiving packets from a specific anchor node is different.The positions of anchor nodes are identical in all three situations, butte= 5, 10 s, and 20 s respectively.The actual time points of receiving a packet from an anchor node are randomly chosen following the exponent distribution.The other settings are the same as those in Example 4.

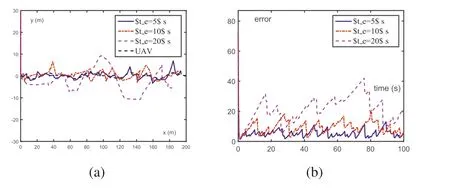
F I G U R E 6 Localisation of a moving AUV via the zeroing neurodynamics model (10) with different te, where te = 5 s (signified by te = 5 s), 10 s (signified by te = 10 s), 20 s (signified by te = 20 s)respectively.The actual movement trajectory of AUV is added for comparison(signified by AUV).(a)Trajectories of x(t).(b)Error e(t).AUV,autonomous underwater vehicle.

The simulation results are visualised in Figure 6, where only the results from zeroing neurodynamics model (10) with error reduction strategies are displayed for convenient comparison.It is worth mentioning that by combining with error reduction strategies, zeroing neurodynamics model (10) reduces locating error by roughly 45% in these three situations.By observing Figure 6, it is evident that the zeroing neurodynamics model (10) can locate the moving AUV with considerable accuracy in all three situations, which proves its effectiveness whenteis much larger than those of previous examples.However, it is also noticeable that the maximum locating error is proportional withte, which is predictable as the error-reducing strategies used in this example are preliminary and demonstrative.Combining zeroing neurodynamics model (10) with more complicated and advanced strategies should be able to effectively counter the locating error ifteis considerably large.

6 | CONCLUSIONS

A zeroing neurodynamics-based method for UASN localisation has been proposed in this paper to preferably locate moving underwater nodes.The methodology of constructing a zeroing neurodynamics model for UASN localisation has been explicated in detail,and several activation functions have been applied to enhance the convergence of the zeroing neurodynamics model.The effectiveness of the zeroing neurodynamics model has been proven via theoretical analyses,which has been verified by illustrative examples.It has also been demonstrated in examples that the proposed zeroing neurodynamics model proposed is compatible with other error-reducing strategies designed for UASN localisation,which has proven that further improvement in the effectiveness and accuracy of the proposed model can be achieved with ease.As the main focus has been zeroing neurodynamics in this paper, the combination with other locating strategies has not been investigated in depth, which will be the direction of future research.

ACKNOWLEDGEMENTS

This work is supported in part by the Key Laboratory of IoT of Qinghai under Grant 2022-ZJ-Y21, in part by the National Natural Science Foundation of China under Grant No.61962052.

CONFLICT OF INTEREST STATEMENT

The authors declare no conflicts of interest.

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are available on request from the corresponding author.The data are not publicly available due to privacy or ethical restrictions.

ORCID

Shuqiao Wanghttps://orcid.org/0000-0002-9426-0174