An embedded vertical‐federated feature selection algorithm based on particle swarm optimisation

Yong Zhang| Ying Hu | Xiaozhi Gao | Dunwei Gong | Yinan Guo |Kaizhou Gao | Wanqiu Zhang

1School of Information and Control Engineering,China University of Mining and Technology,Xuzhou,China

2The Key Laboratory of Symbolic Computation and Knowledge Engineering of Ministry of Education,Jilin University, Changchun,China

3School of Computing,University of Eastern Finland,Kuopio,Finland

4The Macau Institute of Systems Engineering,Macau University of Science and Technology,Taipa,China

Abstract In real life, a large amount of data describing the same learning task may be stored in different institutions (called participants), and these data cannot be shared among participants due to privacy protection.The case that different attributes/features of the same instance are stored in different institutions is called vertically distributed data.The purpose of vertical-federated feature selection (FS) is to reduce the feature dimension of vertical distributed data jointly without sharing local original data so that the feature subset obtained has the same or better performance as the original feature set.To solve this problem,in the paper,an embedded vertical-federated FS algorithm based on particle swarm optimisation(PSO-EVFFS)is proposed by incorporating evolutionary FS into the SecureBoost framework for the first time.By optimising both hyper-parameters of the XGBoost model and feature subsets, PSO-EVFFS can obtain a feature subset, which makes the XGBoost model more accurate.At the same time,since different participants only share insensitive parameters such as model loss function, PSO-EVFFS can effectively ensure the privacy of participants'data.Moreover,an ensemble ranking strategy of feature importance based on the XGBoost tree model is developed to effectively remove irrelevant features on each participant.Finally, the proposed algorithm is applied to 10 test datasets and compared with three typical vertical-federated learning frameworks and two variants of the proposed algorithm with different initialisation strategies.Experimental results show that the proposed algorithm can significantly improve the classification performance of selected feature subsets while fully protecting the data privacy of all participants.

K E Y W O R D S Evolutionary optimization, feature selection, privacy protection, vertical-federated learning

1 | INTRODUCTION

Feature selection (FS) is one of the most important preprocessing techniques in data mining and machine learning.It aims to optimise the performance indicators (such as classification accuracy) while reducing the learning cost, by deleting redundant or irrelevant features from the original dataset [1].At present,FS algorithms have been widely used to solve many practical problems, such as hyper-spectral image analysis [2],visual target tracking [3], protein methylation sites prediction[4] and power grid intrusion detection [5].

In recent years, with the gradual popularisation of big data technology, more and more data describing the same learning task in many practical problems are distributed and stored in different participants.Generally, those data are distributed among participants in one of the following two ways.The first is horizontal distribution, in which different participants have different instance IDs but the same features, such as customer data stored by different banks, and typical case data collected by different hospitals.The other is vertical distribution, in which different participants have the same instance IDs but different features.For example, banks and e-commerce companies have payment behaviour and shopping record of the same user, respectively.Compared with the horizontal distribution data that label information can be used by all participants, it is more difficult to learn the modelling of vertical distribution data because their labels related to the learning task are only distributed on one participant and cannot be shared among all participants.The purpose of vertical-federated FS is to jointly reduce the feature dimension of vertical distributed data in the case that participants do not share local original data, so as to establish a globally optimal learning model [6].

To deal with traditional FS problems, scholars have proposed many types of FS algorithms, such as filter FS [7] and evolutionary FS [8].However,there are relatively few research studies on FS under privacy protection.According to the different insertion timing of privacy protection mechanism,the existing methods can be roughly divided into two categories:passive FS approach and active FS approach.The former approach first executes the FS process on the original data and then uses the anonymous mechanism to process those sensitive features in the optimal feature subset until the third party cannot identify them [9, 10].The latter approach integrates privacy protection into the FS process and deletes as many features with high privacy relevance as possible on the premise of ensuring the accuracy of results [11–13].The above two approaches effectively solve the privacy problem in the process of data transmission or sharing, but existing methods are oriented to the scenario of centralised data storage, so they are not suitable for the distributed FS problem considered in this paper.In view of the horizontally distributed storage of data,a privacy perception collaborative information sharing framework is proposed in the literature in Ref.[14].By eliminating the most irrelevant feature sets in terms of accuracy and privacy, the method can not only ensure the privacy of data but also improve the classification performance of data.However,since original data can be shared between participants, these methods still leak sensitive data.

FS based on evolutionary optimisation is called evolutionary FS.Since it can find the optimal or sub-optimal solutions of the problem through global search strategy, it has become a hot technology to solve FS problems in recent years [8].Various typical evolutionary optimisation algorithms, such as genetic algorithm[15],differential evolution[16],ant colony algorithm[17], and artificial bee colony algorithm [18], have been successfully applied in FS problems.As a relatively new evolutionary optimisation technique, particle swarm optimisation(PSO) [19] has the advantages of simple concept, convenient implementation and fast convergence,so scholars have tried to apply it to FS problems[20,21].Although these evolutionary FS algorithms significantly improve the classification accuracy of feature subset, most of them are oriented to centrally stored data and cannot effectively deal with the multi-participant FS problem in distributed data storage.Although a few scholars have successfully applied evolutionary optimisation to distributed FS problems [22], they still require participants to share sensitive information including original data and labels.

Compared with traditional FS problems, the challenge of federated FS problems on vertical-distributed data is that participants cannot share their original data and other sensitive data due to the limitation of data privacy.In particular, the labels related to the learning task are only distributed on one participant, and different participants cannot share these labels.In order to build a more excellent learning model, however, participants can share some insensitive model parameters.Federated learning can jointly establish a virtual common model[23,24] through exchanging model parameters under encryption mechanism, rather than the original data themselves.Learning for vertical distributed data is called vertical-federated learning.As a new vertical-federated learning framework,SecureBoost is able to build an XGBoost tree enhanced model across multiple participants while maintaining data privacy and achieving classification accuracy, compared to non-federated learning algorithms for centrally stored data[25].

In this paper,an embedded vertical-federated FS algorithm based on PSO is proposed by incorporating evolutionary FS techniques into SecureBoost framework.Different from existing FS algorithms, this algorithm optimises both hyperparameters of XGBoost tree model and feature subsets in order to obtain an optimal feature subset that makes XGBoost model more accurate.To our knowledge,this paper is the first work to study FS problems in vertical-federated learning scenarios.The main contributions of this paper are as follows:

• An embedded vertical-federated FS framework based on evolutionary optimisation is proposed for the first time.By effectively combining the global optimisation capability of evolutionary FS method with the excellent multi-participant joint learning characteristic of SecureBoost, the proposed framework provides a new and effective solution to the vertical-federated FS problem.

• A multi-participant cooperative PSO algorithm for cooptimising model hyper-parameters and feature subsets is presented.In this algorithm, the hyper-parameters of XGBoost model and feature subsets are optimised synchronously so that we can obtain an optimal feature subset that makes XGBoost model more accurate.

• A feature importance-guided particle swarm initialisation strategy is proposed.By increasing the probability of important features to be selected, the strategy can generate high-quality initial swarm and improve the search efficiency of PSO.

The paper is organised as follows: Section 2 reviews the related work.Section 3 describes the vertical-federated FS problem.In Section 3, the proposed embedded verticalfederated FS algorithm is proposed.In Section 5, the performance of the proposed algorithm is analysed experimentally.Finally, Section 6 concludes the whole paper.

2 | RELATED WORK

This section provides a brief introduction about the background knowledge and related work.

2.1 | Traditional feature selection algorithms

Supposing that a data set containsDfeatures andLsamples,and the set of original features isF, a traditional FS problem can be described as follows: selectingdfeatures (d≤D)fromFto maximise a specified indicatorH(⋅).Specifically, in the background of data classification, the aim of FS is to select a feature subsetX⊆Fhaving the highest classification accuracy [26].

According to the combination way of evaluation indicator and classifier, existing FS methods can be divided into three categories: filter, embedded and wrapper.The filter approach calculates the importance of each feature and sorts all features according to their importance.Some typical methods include ReliefF [27], mutual information method [28], correlation coefficient method [29] etc.Since it is independent of any learning algorithm, the computational cost of this approach is relatively small.However,its classification accuracy is generally inferior to the other two approaches because its results still contain a lot of redundancy features.

The wrapper approach directly takes the performance of classifier as a criterion to evaluate feature subsets; it shows high classification accuracy.Some typical methods include the evolutionary FS algorithm combining KNN and SVM[8, 30].Because the classifier needs to be used repeatedly to evaluate the quality of feature subsets, the calculation cost of this approach is relatively high.The embedded approach takes the FS process as a part of learning algorithm and selects feature subsets while implementing the learning algorithm.Some typical methods include penalty term-based embedded FS [31] and tree model-based embedded FS[32].Among them, tree model-based FS has become the most commonly used method due to its advantage of natural allocation of feature importance [32, 33].As selected feature subsets are closely related to learning algorithms, the feature subset obtained by the embedded method can only improve the performance of the currently used learning algorithm [34].

2.2 | Evolutionary feature selection

In 1989, Siedlecki et al.[35] first applied genetic algorithm to FS.Subsequently, various typical evolutionary or swarm intelligence algorithms are successively applied to FS [15–18].In 2016, Xue et al.[8] summarised the current research status of evolutionary FS in detail.Further, in 2020, Nguyen et al.[36]analysed the latest evolutionary FS algorithms, especially the FS algorithms based on swarm intelligence.Since this paper focusses on PSO,the following contents just summarise PSObased FS algorithms.

Existing PSO-based FS algorithms are mainly for the case with centralised data storage.Xue et al.[37] proposed three new population initialisation strategies and three particle updating mechanisms in view of the defects of traditional PSO.Tran et al.[38] proposed a potential PSO algorithm considering both sample value discretisation and FS problem.The algorithm uses PSO to find potential good breakpoints for discretisation and FS process automatically.Subsequently,Tran et al.[39] proposed a variable length particle swarm FS algorithm.By effectively reducing the search space of the population, the algorithm significantly improves the solution performance of population.Further, Song et al.[21] divided the high-dimensional feature space into multiple sub-spaces according to the feature importance and proposed a cooperative co-evolutionary PSO algorithm, which significantly improved the ability of PSO to deal with high-dimensional FS problems.Li et al.[40] proposed an improved sticky binary particle swarm FS algorithm.By introducing a featureweighted information initialisation strategy and a dynamic bit masking strategy, the algorithm significantly improves the search performance of population.Xue et al.[20]proposed an adaptive PSO algorithm based on multiple classifiers by automatically adjusting search operators and control parameters in the evolution process.In addition, Han et al.[41]regarded the FS problem as a multi-objective optimisation problem and proposed a multi-objective adaptive PSO algorithm for FS, where the selective pressure of population is improved by adjusting penalty value adaptively.

The above methods significantly improve the ability of PSO to deal with FS problems, especially in the high-dimensional/large-scale FS problems.However, they are all for the case with data-oriented centralised storage.At present, a few scholars have applied evolutionary FS method to the case of data-oriented distributed storage.Huang et al.[42]proposed a distributed parallel FS framework of mixed PSO-SVM, in which PSO is run on the server and SVM is trained on clients.This framework significantly reduces the running time of PSO and improves the running efficiency of algorithm.However,it still needs the server and clients to share sensitive information such as labels, which cannot effectively protect data privacy.For vertical-federated FS problem under privacy protection,how to establish an effective non-sensitive information sharing mechanism among participants is still an open problem.

2.3 | Feature selection under privacy protection

To date, there are still few research results on FS problems under privacy protection, let alone the case involving multiple participants.Considering the case that participants can share the original data, Bhuyan et al.[43] used disturbance and fuzzification strategies to process the data collected by participants for protecting the transmission security of data and proposed a distributed FS method based on the fuzzy model.Moreover,in order to protect the cloud environment from external attacks,Abdullayeva [44] developed an effective method detecting cyberattacks, where the Pearson correlation method is used to extract the most informative features.However,these methods need to interact with the underlying data,so there is still a risk of privacy leakage if one of those participants is not trusted.In addition,in order to prevent private data from being stolen or observed by malicious third parties, an appropriate underlying security summation protocol [6, 45] can guarantee the safe transmission of data between participants.Based on this idea,Lu et al.[45] proposed a distributed integrated FS method under privacy protection,in which the data of each participant can be securely transmitted through encryption.However,since all data need to be transmitted between participants, the communication cost of this method is relatively high.Most of all, since the original data can be transmitted freely between participants, this algorithm cannot completely protect the privacy of each participant.

Considering the case that sensitive information cannot be shared among participants,Jafer et al.[46]evaluated the privacy level of each feature by sharing the feature distribution information among participants and ranked features according to the privacy and classification performance levels.In this method,only non-sensitive parameters are transmitted between participants for ensuring the privacy of sensitive data.Sheikhalishahi et al.[14]evaluated the privacy score of each feature by using the number of records that fall within a certain interval,calculated the utility score of each feature by using filtering strategies such as mutual information, and then proposed a privacy-utility FS algorithm.Then,Qin et al.[47]presented a federated learningbased FS algorithm in network intrusion detection.In the algorithm,a greedy FS method is used to select features that can achieve better accuracy regarding different attack categories,and multiple global models are generated by the server in federated learning.However,the selected feature subset obtained by these two algorithms may still contain a lot of redundant features,because it inherits the defectsof traditional filtering FS approach.Recently, Hu et al.[48] proposed a multi-participant federated evolutionary FS algorithm for imbalanced data.Here, a multilevel joint sample filling strategy and a federated evolutionary FS method are developed to improve the performance of the FS algorithm.However,the scenarios considered in the above results are all horizontally distributed data,that is,the data of each participant has the same attributes/features and different instance IDs.Therefore,the above algorithms are not suitable for the vertical-federated FS problem considered in this paper.

2.4 | The framework of SecureBoost

SecureBoost is a recently proposed lossless privacy protection tree enhancement framework for vertical-distributed data[25].SecureBoost is able to build an XGBoost tree enhancement system across multiple participants[49]through a homomorphic encryption strategy.Since the XGBoost tree enhancement system can select the feature with the most obvious classification effect when splitting each node,the system can indirectly complete the FS process.Specifically,the importance of features can be ranked by counting the split times of features on nodes[50].The SecureBoost framework consists of two core parts: entity alignment(i.e.matching sample IDs)and identifying the hyperparameters passed during model training and their transmission way.The purpose of entity alignment is to find samples/instances with the same ID from participants without compromising any data privacy.The second core part aims to build a complete XGBoost tree enhancement model with multiple participants under the premise of protecting data privacy.

Similar to gradient boosting decision tree (GBDT), the XGBoost tree enhancement model also uses the CART regression tree as the base classifier and executes multiple iterations by using the residuals of the previous tree as input of the next tree.When constructing the XGBoost tree model,the following two key issues need to be considered.One is the construction of the objective function (i.e.the loss function);another is the selection of both split nodes and their split values.From the perspective of leaf nodes,the loss function of the model can be defined as:

In the above equation, the first two items correspond to the loss function values of the left child node and right child node after splitting, respectively, and the third item corresponds to the loss function value of the node before splitting.The greater the Gain value, the greater the loss value reduced after splitting.When a node is segmented,all features and their values on the node are traversed,and the feature and its value corresponding to the maximum Gain value are selected for segmentation.

As can be seen from the above analysis,giandhiare the key to build the XGBoost model.Since they belong to the intermediate values of the model loss function, the above process does not involve any sensitive information on the original data.Therefore, after performing homomorphic encryption ongiandhi, they can be transmitted among different participants and their encrypted result can be denoted by [gi] and [hi], where [⋅] is the homomorphic encryption function.In addition,the same sample distributed on different participants can be marked by the same ID.Thus, the information transmitted between participants in the SecureBoost framework is{IDi,[gi],[hi]}.Taking the construction of a tree as an example, the SecureBoost framework is as follows:

Step 1: The active participant constructs the root node based on all training samples and adds it into the node queue.

Step 2: The passive participant waits for the sample information(i.e.the sample IDs)on the current node from the active participant, together with the loss function information after encryption of relevant samples(i.e.[g]and[h]in formula(1)).

Step 3: Based on the above information, the passive participant calculates the segmentation aggregation gradient information on its own data and feeds back it to the active participant, based on which the active participant calculates the optimal segmentation point (i.e.optimal segmentation feature) on the current node.

Step 4: The passive participant with the optimal segmentation feature receives the optimal segmentation feature number and the optimal segmentation threshold index(i.e.the box index), determines the specific optimal segmentation threshold value, and splits the current sample space on that passive participant.At the same time,the segmentation result is sent back to the active participant.

Step 5: The active participant splits the current tree node into two child nodes according to the received sub-sample space and adds them into the node queue.

Step 6: Judge whether the tree depth meets the maximum depth.If so, stop the algorithm and output the tree;otherwise, return to Step 2.

3 | PROBLEM DESCRIPTION

In Figure 1,the participant holding labels is called the active participant, and the remaining participants without labels are collectively called passive participants.Different from horizontally-federated learning [51], vertical-federated learning does not require an additional third party(server)to coordinate the work of participants, and the active participant directly undertakes the role of the server.This is because only the active participant owns the class label, and these labels are extremely precious and contain a lot of private information.Therefore,only the active participant holding the label information can model the problem, while the passive participants cannot independently model the problem due to the lack of labels.However, the passive participants can assist the active participant in modelling by transmitting intermediate parameters.

In the above formula,FL represents the federated learning algorithm running on the active participant, andJactiverepresents the performance index value of FL.Considering the context of classification, the performance indexJcan be expressed as the classification accuracy or the AUC.

4 | THE PROPOSED PSO‐BASED VERTICAL‐FEDERATED FEATURE SELECTION ALGORITHM

The section introduces the proposed embedded verticalfederated FS algorithm based on PSO (PSO-EVFFS), by integrating the PSO-based FS technique into SecureBoost framework.First, the basic framework of PSO-EVFFS is given.Second, an integrated ranking strategy of feature based on XGBoost is developed to remove irrelevant features from each participant.Then, the hyper-parameters of XGBoost model and feature subset are expressed as an optimised solution jointly,and a multi-participant cooperative PSO algorithm is proposed for co-optimising model hyper-parameters and feature subset.Finally, the communication and computation cost of PSO-EVFFS is analysed.

4.1 | The algorithm framework

F I G U R E 1 Data distribution scenario considered in vertical-federated feature selection (FS) problems

The proposed embedded vertical-federated FS algorithm integrates the FS process into the SecureBoost framework.Suppose that the current system containsMparticipants,namely party-1, party-2, …, party-M.Among them, only the party-1 holding class labels is the active participant, while all the other participants are all passive.To ensure the security of data,the learning model is only built on the active participant,the passive participants do not exchange any data, but the active participant can collect the information of intermediate non-sensitive parameters obtained by passive participants.

Figure 2 shows the framework of the proposed algorithm.The framework consists of two main phases.In the first stage,the importance degree of each feature is obtained, and irrelevant features whose importance degrees is 0 are deleted from each participant.First, under the SecureBoost framework,participants jointly train multiple XGBoost tree models and count the average number of split times for each feature.Then,the mean split times are used to describe the importance of each feature.If the split times of a feature is 0, its importance degree is 0, so it is an irrelevant feature.In the second stage,the multi-participant cooperative PSO algorithm is used to search optimal hyper-parameters of XGBoost model and optimal feature subset simultaneously under the SecureBoost framework.

On the one hand, the population/swarm evolves only on the active participant, whose purpose is to search for an optimal feature subset as well as a set of optimal hyperparameters for the XGBoost model.On the other hand,the fitness value (i.e.classification accuracy) of each particle can only be evaluated on the active participant.Specifically,the XGBoost model on the active participant is used as a classifier to evaluate the fitness of each particle.The role of the passive participant is to assist the active participant to build the XGBoost tree model under the SecureBoost framework.The optimal feature subset corresponding to each passive participant is searched only by the active participant.

In the proposed framework, the main functions of the active participant are as follows: ①establishing multi-group XGBoost tree models by uniting multiple participants under the SecureBoost framework, counting the average split times of feature in the XGBoost tree model, calculating the comprehensive ranking of features, and deleting irrelevant features; ②in the process of executing the PSO-based FS algorithm, constructing the tree model by integrating the intermediate parameters obtained by multiple participants and calculating the fitness value of each particle according to the information on the leaf node of the tree model; ③transferring the index values of the selected features in the evaluated particle to the corresponding passive participant; ④when the algorithm terminates, outputting the optimal solution, that is, the optimal feature subset and hyper-parameter values are obtained.

The main function of a passive participant is to calculate the importance degree of features held and assist the active participant to construct the XGBoost tree model.Since the data on each passive participant has no labels, passive participants do not perform FS operation independently.It should be noted that although the whole population evolves only on the active participant,its search space consists of all features on all participants.When a passive participant receives the index values of selected features transmitted by the active participant,it first uses these index values to determine those specific selected features and then reduces the dimension of own data based on those selected features.Finally, on the basis of the dataset after dimensionality reduction, the passive participant assists the active participant in constructing nodes in the XGBoost tree model.Each passive participant calculates the importance degree of a feature by counting the times that the feature participates in node splitting.

The information to be transmitted between the active participant and the passive participants includes the following: ① the split times of features obtained by the passive participant with the help of XGBoost tree model in the first stage, as well as the loss function information.Both types of information are transmitted from the passive participant to the active participant; ②in the second stage,index values of features selected by particles (i.e.feature subsets) and loss function information obtained by the passive participant based on those selected features.The index values are transmitted from the active participant to the passive participant.After the passive participant obtains the above information, it will transmit the loss function information obtained by those selected features to the active participant, based on which the active participant builds the XGBoost tree model.It can be seen that similar to the SecureBoost framework, the framework proposed in this paper does not need to transmit sensitive information such as features and labels, so it can ensure the data privacy of all participants to the maximum extent.

F I G U R E 2 The framework of PSO-EVFFS

4.2 | The first stage: removing irrelevant features

As mentioned above, when needing to split a node, the XGBoost tree model will select the feature with the best classification effect at present to split [50].In view of it,this paper estimates the importance of a feature by counting the split times of the feature on nodes.Since the model's hyper-parameters significantly affect the performance of the XGBoost tree model,HXGBoost tree models are jointly established under the SecureBoost framework, and the average split times of each feature in these tree models are used to estimate its importance degree.

Algorithm 1 Specific steps of calculating the importance degrees of features (supposing the party-1 is the active participant)Input: The sample set held by the k-th participant Ωk, and corresponding features Γk, k = 1, 2, …, M;Output: The importance degrees of features held by each participant Imv(k),k = 1, 2, …, M;1: Initialise hyper-parameters of H XGBoost models on the active participant;2: For h = 1: H // Obtain the split times of features according to the H XGBoost models in turn 3: Count the split times of all features held by each participant under the SecureBoost framework [24].Let the split times of all features held by the k-th participant as get_fscoreh(k), k = 1, 2, …, M;4: Normalise these feature split times on each participant;5: End for 6: For k = 1: M //Calculate the average split times of features held on each participant 7: Calculate the average split times of feature held by the k-th participant,that is, get_fscoreh(k) = 1HΣH h=1 get_fscoreh(k);8: Imv(k) = get_fscoreh(k);9: Delete those features whose Imv(k) values are 0;10: End for 11: Output the vector of feature importance degree of M participants, that is, Imv(k),k = 1, 2, …, M;

Algorithm 1 gives the calculation process of the importance degrees of features.Here,each passive participant needs to use the XGBoost model constructed by the active participant to count the split times of features.The SecureBoost framework is still used to count the split times of features(Lines 1-3 of Algorithm 1).When the active participant builds an XGBoost tree model,it can obtain the split times of features held by each passive participant, denoted by get_fscoreh(k),k= 1, 2, …,M,h= 1, 2, …,H.To prevent the third party from stealing the data distribution information by analysing the split times of features, the split times of features obtained by each participant will be normalised (Line 4 in Algorithm 1).Afterwards, the average split times of each feature on theHXGBoost models are calculated; these average values are the importance degrees of these features and stored into Imv(k).When the importance degree of a feature is equal to 0,that is,its split time is equal to 0; this indicates that the feature has very little influence on labels.To a large extent, it is an irrelevant feature that can be removed directly.Finally, each passive participant transmits Imv(k) and its feature indexes to the active participant,and the active participant performs rank features by integrating their importance degrees.

It should be noted that although the active participant has the whole tree,it only knows the indexes of those split features held by passive participants, but does not know any sensitive information including the split threshold and feature name.Specifically, in the process of constructing tree models, only non-sensitive information such as feature indexes and loss functions is transmitted between the active participant and the passive participants.Therefore, like the SecureBoost framework, Algorithm 1 will not disclose any sensitive information.

4.3 | The second stage: optimising hyper‐parameters and feature subset

After removing irrelevant features from each participant in the first stage, the stage develops a multi-participant cooperative PSO algorithm to delete redundant features from remaining features, that is, to find the optimal feature subset.Since the construction of XGBoost tree model requires setting corresponding hyper-parameters and the optimal feature subsets corresponding to different hyper-parameters are different,it is necessary to search for the optimal hyper-parameters of XGBoost when searching the optimal feature subset.Supposing that the first participant is the active participant,according to the general description of the vertical-federated FS problem given in Equation (3), the objective function and constraints of the problem can be described as follows:

First, a problem characteristic-oriented hybrid particle coding strategy is presented.Then, a swarm initialisation strategy guided by feature importance is designed.Following that, a new update rule for mixed coding particles is given.Finally, an evaluation strategy of particle is introduced.

Algorithm 2 Multi-participant cooperative evaluation strategy for particles (Taking the particle X1 as example)Input: Particle X1 on the active participant, the sample space, Ω;Output: AUC(X1) output by the active participant;%%%%%%%——————————-- The operation on active participant————————--1: Decode the particle X1 according to the method in Section 4.3 (1);2: Use the hyper-parameters obtained by X1 to determine the structural attributes of the XGBoost tree;3: Transmit the indexes of features selected by the particle from the active participant to corresponding passive participants;4:While the number of trees q ≤TD1 do//The termination condition for constructing the tree model 5: Construct the q-th tree under the SecureBoost framework, denoted by Tree(q);6: While the depth of the tree p ≤TN1 do 7: For the number of nodes in the tree = 1:2p 8: Transmit the IDs of samples to be processed to all passive participants in turn;9: Receive the passive participant's loss function for each selected feature;10: According to Equation (2) in Section 2.4, determine the optimal segmentation feature for the current node, and transmit the feature number and the optimal segmentation threshold to the passive participant holding the feature;11: Receive the segmentation record about the sample space on the passive participant, and split the current tree node into two child nodes;12: End for 13: Construct the p-th layer of the Tree(q);14: p = p +1;15: End while 16: q = q+1;17: End while 18:Calculate the AUC value of X1 using the test dataset based on the established XGBoost tree model;%%%%%%%—————————————— The operation on passive participants (Take the j-th passive participant as an example)————————————————-19: Receive the indexes of selected feature transmitted from the active participant, and determine the specific selected features;20: Use these selected features to reduce the dimension of the dataset;21: While the size of samples received nsam ≤Nsam do //Nsam is the total number of valid samples 22: Receive the IDs of samples to be processed transmitted from the active participant,and determine the sample data to be processed currently;23: Calculate the loss function information of all selected features based on these samples;24: Feedback the loss function information to the active participant;25: Receive the optimal segmentation feature number and the optimal segmentation threshold transmitted from the active participant, segment the sample, and transmit the segmented sample space to the active participant;26: nsam = nsam +1;27: Wait for the new sample IDs;28: End while?

(1) Mixed encoding and decoding strategy for particles

On the one hand, as mentioned above, the whole swarm only evolves on the active participant, with the aim of finding both the optimal feature subset and the optimal hyperparameters of XGBoost.On the other hand, since each participant contains only a part of features, the best feature subset should be produced by the joint cooperation of all participants.In view of this, in this section, a mixed encoding strategy with real numbers and integers is developed to represent a candidate solution, that is, a particle.

F I G U R E 3 The mixed particle coding strategy

Let the participant party-1 be the active participant.In general, the hyper-parameters of XGBoost tree model include the number of trees(TD),the depth of trees(TN),the number of boxes (BN), and two regular-term parameters used in the loss function(γandλ).Integer encoding is adopted for these 5 hyper-parameters.For feature sets,a real encoding within[0,1]is adopted,and the probability of each feature being selected is taken as its element.Taking theith particle as an example,Figure 3 shows the mixed coding strategy of a particle on the active participant.Here,the first 5 elements correspond to the 5 hyper-parameters to be optimised, and the last ΣMk=1Dkelements correspond to the features selected byMparticipants.xki,j∈[0,1] represents the probability that thejth feature is selected on thekth participant, andDkrepresents the feature dimension on thekth participant.

When calculating the fitness of a particle, the method in Ref.[52] is used to decode the particle.Taking the particleXias an example,whenxki,j>rand,thejth feature held by party-kis selected into the feature subset;Otherwise,it is not selected.For the hyper-parameter part, the elements of the particle are decoded by the rounding function.

(2) Swarm initialisation strategy guided by feature importance

Oh! you fool, said she, then we must all four die of hunger, and you may just as well go and plane the boards for our coffins ; and she left him no peace till he consented

This section presents a feature importance-guided swarm initialisation strategy (FIIS) to generate high-quality initial swarm.As mentioned above, each particle on the active participant contains two parts: hyper-parameters of XGBoost and feature subsets.For the 5 hyper-parameters,if the number of trees(TD)is set to be too small or the tree depth(TN)is set to be too low, then the split chance of a feature is too low,resulting in too many 0 elements in the split time vector of feature, further making the system under fitting.Therefore,these 2 hyper-parameters should take larger values in the initialisation process.In this paper, they are randomly selected within [(1/2)σmax,σmax].

The box number (BN) affects the feature segmentation threshold,and differentγandλvalues affect the calculation of loss function.For these 3 hyper-parameters, their values are randomly selected within [σmin,σmax] when initialising the swarm.Here,σminandσmaxare the upper and lower limits of hyper-parameter values, respectively, and havingσmin< (1/2)σmax.

For the feature part, the feature importance degrees are obtained in Section 4.2 is used to guide its initialisation.The bigger the importance degree of a feature, the higher the probability it is increased.Based on this, the following rule is used to initialise the feature part of a particle:

In the above formula, the parameterαis a control coefficient,which is used to adjust the diversity and convergence of the initial swarm, 0 <α≤0.5.The larger the valueαis, the better the diversity of the initial swarm is, while the fitness values of the initial particles are relatively worse.When settingα= 0.4, after initialising a particle using formula (5), all the features whose ranking values are within[1,0.1 ⋅|F|]will get a random value within [0.23, 1], and those features whose ranking values are within[0.9 ⋅|F|,|F|]will get a random value within[0,0.77].The values of remaining features are randomly set within [0, 1].

(3) Multi-participant cooperative evaluation strategy for particles

This section discusses the fitness evaluation strategy of particle on the active participant.As described in Section 4.3,each particle needs to search for both the optimal feature subset and the tree model hyper-parameters,and they together determine the performance of the classifier.Therefore, the proposed particle evaluation strategy should be able to evaluate the quality of both hyper-parameters and feature subsets.More importantly, the active participant contains only partial features, and it cannot exchange sensitive information with other participants.In order to effectively joint all participants to evaluate the fitness of a particle, this section presents a multiparticipant cooperative evaluation strategy oriented to mixed coding particles, Algorithm 2 shows its specific process.Without loss of generality, a dataset is also randomly divided into training and test sets.

For a particle to be evaluated on the active participant,first,it is decoded according to the method in Section 4.3 (1) (Line 1).Second, the active participant uses the hyper-parameter values obtained by the particle to determine the structural attributes of the XGBoost tree (Line 2).Then, the active participant transmits the indexes of these features selected by the particle to corresponding passive participants (Line 3).Following that, the XGBoost tree model is constructed under the SecureBoost framework based on the training dataset(Lines 4–15).Finally, the AUC value of the current particle is calculated using the testing dataset.

(4) Execution steps of the proposed multi-participant cooperative PSO algorithm

wherer1andr2are the random numbers within [0,1],respectively,d=1,2,…,5+|F|.Pbesti(t) and Gbesti(t)represent the personal leader and global leader of theith particle at thetth generation, respectively.

Step 6: Determine whether the termination condition is met.If yes,output the final result; otherwise,lett=t+1,and return to Step3.

4.4 | Cost or complexity analyses

1) Communication cost: The communicate cost of the proposed algorithm mainly focusses on the following two stages.It is noted that only the active and passive participants can transfer information in the whole framework,while there is no communication between passive participants.

Stage 1: removing irrelevant features.Since the communication cost required for ranking features is relatively small compared to that required for building the tree model,it can be ignored here.Here only the communication times required for constructing the tree model are counted.When constructing a node of the tree,①the information transmitted from the active participant to the passive participant is the loss function{IDi,[gi], [hi]} and the optimal segmentation feature information{the optimal segmentation feature number, and the optimal segmentation threshold},i=1,2,…,N,Nis the total number of samples.Compared with the former, the amount of information transmitted by the latter can be negligible.The information unit{IDi,[gi],[hi]}needs to be transmittedM-1 times,

whereMis the total number of participants.②The information transmitted from the passive participant to the active participant is {[Gk], [Hk]} and the segmented sample space index[Gk],[Hk]corresponds to the segmentation features and the segmentation aggregation gradient information on the passive participant-k,k= 2…,M.Compared with the former,the amount of information transmitted by the latter can be negligible.Unit{[Gk],[Hk]}also needs to transmitM-1 times.Therefore, when constructing a node, the total number of communications required is 2 (M- 1).Assuming that the number of trees to be constructed by XGBoost model is TD and the tree depth is TN, then the total number of communications required to construct a tree is 2×TD×(2TN+1-1)× (M- 1).

Stage 2:optimising hyper-parameters and feature subset by the proposed PSO.The information transmitted in an iteration of the PSO includes the information required to build an XGBoost tree model for each particle as well as the feature indexes transmitted from the active participant to the passive participant.Compared with the former, the amount of information transmitted by the latter can be also negligible.In view of this,the communication times required for each iteration of the algorithm ispopsize⋅(2 × TD × (2TN+1- 1) + 1) ×(M-1),wherepopsizeis the size of the swarm.As can be seen that except for the communication cost required in the SecureBoost framework, the remaining communication cost is mainly determined by popsize.Therefore, the communication cost of the PSO can be reduced by adjusting the value of popsize.Of course,a smaller value of popsize will decrease the search performance of PSO.

2) Computational complexity or cost: The computational cost of the proposed algorithm also includes the following two stages.It is noted that although part of the calculation cost of the algorithm is distributed among different passive participants, it is also counted in the total calculation cost here.

Stage 1: removing irrelevant features.The calculation cost of this stage mainly focusses on the calculation of the loss function and the optimal segmentation points.Compared with their calculation cost,the calculation cost of ranking features is relatively small and can be expressed linearly.During calculating the loss function, the values of {Gk,Hk} on all participants need to be calculated based on the values ofgiandhifrom

To sum up, the calculation cost of the whole algorithm is mainly determined by the calculation times of the loss functions and the optimal segmentation points, while the cost of calculating the two kinds of information is mainly determined by the number of features and the model parameters(TD,TN and BN).When the model parameters are fixed,the larger the number of features in a dataset, the higher the computational complexity of the algorithm.The main objective of this paper is to reduce the number of features in the dataset while improving the performance of XGBoost model.

5 | EXPERIMENTS

In order to verify the performance of the proposed PSOEVFFS algorithm, this section applies it to 10 datasets.The experiment is divided into five parts as follows:Part 1 introduces the datasets used and the way they use.In parts 2 and 3, the comparison algorithms and performance indicators used in the experiment are described.Part 4 analyses the influence of key parameters on the performance of PSO-EVFFS.In part 5,the experimental results are given and analysed.All algorithms are programed in Python and run on dual-core 3.0 GHz and 8G PC.

5.1 | Datasets and usage way

Each dataset is assigned toMparticipants(including one active participant andM-1 passive participants) by the random and uniform division way.For a dataset, first, all samples are randomly shuffled.Here,the first 70%samples are taken as the training set and the last 30% samples are taken as the test set for horizontal segmentation.After that, all the samples are vertically segmented intoMgroups, and each group is randomly assigned to a participant.In this process,class labels are first taken out and placed on the active participant.Based on the way, each participant can get a training set with 70%samples and a testing set with 30%samples.The datasets used in the experiment are shown in Table 1.

5.2 | Comparison algorithms

To verify the advantages of the proposed PSO-EVFFS algorithm in classification performance, it is first compared with the standard SecureBoost framework [25] and two verticalfederated learning frameworks.One is the vertical-federated learning framework based on logistic regression proposed in the literature in Ref.[53] (denoted as VFLR).In order to facilitate the aggregation of intermediate gradients in the federated framework, VFLR performs a second-order approximation to the loss function and uses the quasinewton method for derivation.The convergence rate of the quasi-newton method is much faster than that of the gradient descent method, so the convergence rate of the VFLR is greatly improved.Another is the vertical-federated training framework of deep neural network model for privacy protection proposed in the literature in Ref.[54] (denoted as VFDNN).By aggregating gradient information, this methodcan achieve similar classification accuracy to the centralised DNN scheme while protecting data privacy.

T A B L E 1 The datasets used

T A B L E 2 Parameters of all the algorithms

The parameter settings of the proposed PSO-EVFFS and comparison algorithms are shown in Table 2.For VFLR and VFDNN, their other parameters are set according to the original literature in Ref.[53, 54], respectively.

5.3 | Performance indicators

In this paper,AUC[55],Classification accuracy(ACC)[21]and F-Measure[56]are used as evaluation indicators.Among them,ACC is commonly used to evaluate the classification performance of balanced data.AUC and F-Measure are two types of comprehensive evaluation indicators, which can evaluate both balanced and unbalanced data.

(1) AUC

The AUC value is the area under the ROC curve, and the larger the value,the better.For a binary classification problem,denoted by AUC =S(ROC), the horizontal and vertical coordinates of ROC curve are:

where TP represents the number of positive samples correctly classified; FP represents the number of positive samples misclassified; FN represents the number of negative samples misclassified; TN represents the number of negative samples correctly classified.

For a multi-classification problem, the AUC value is:

whereKrepresents the total number of classes, and ROCirepresents the ROC curves derived from samples in the classiand all other classes.

(2) ACC

The ACC value describes the proportion of correctly classified samples to the total number of samples.For a binary classification problem, the calculation formula is as follows:

For a multi-classification problem, the calculation formula of ACC is as follows:

whereTrepresents the number of all correctly classified samples,Frepresents the number of all incorrectly classified samples, andT+Frepresents the total number of samples.

(3) F-measure

F-measure indicator is the weighted harmonic average of Precision (P) and Recall (R).For a binary classification problem, the calculation formula is as follows:

For a multi-classification problem, the F-measure value is as follows:

whereF- measureirepresents the two-category F-measure values derived from samples in the classiand all non-classi.When the valueβis set to be 1, the F-measure value is F1-score [25].

5.4 | Parameter sensitivity analyses

(1) Control parameterα

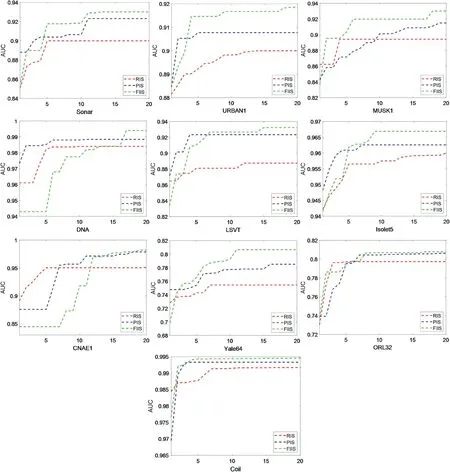
In Section 4.3 (2), the control parameterα(0 <α≤0.5)directly affects the quality of the initial swarm.It can be seen that the larger the valueαis, the better the diversity of the initial swarm is, but the worse its convergence is.Taking the case of three participants as an example and setting the value ofαto be 0.1, 0.2, 0.3, 0.4, and 0.5 in turn, Figure 4 shows the box-plots of AUC obtained by PSO-EVFFS under differentαvalues.

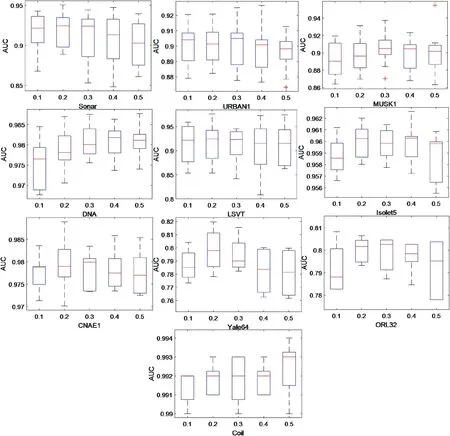
F I G U R E 4 Box-plots of AUC obtained by the proposed algorithm under different α values

It can be seen from Figure 4 that ①with the increase of theαvalue, the algorithm achieves the maximum average AUC values on 6 out of 10 datasets whenα=0.3,although the AUC values obtained by PSO-EVFFS all show different change rules on the 10 datasets;②more importantly,the value ofαhas little influence on the algorithm performance.Taking the data set, URBAN1, as an example, whenα= 0.3, the algorithm obtains the maximum AUC value of 0.9013,and whenα=0.5,the algorithm obtains the AUC value of 0.8964, and the difference between the two is only 0.54%.Under differentαvalues, the dataset ORL32 shows the largest performance deviation, which is only 1.44%.Taking the above results into consideration, theαvalue is set to 0.3 in subsequent experiments.

(2) Number of participantsM

This part discusses the influence of the number of participants (M) on the algorithm performance.Considering that there are not too many cooperative enterprises involved in privacy protection in practical application, the number of participants is set as 2,3 and 5,respectively,in the experiment.Data is independent and invisible between participants.At the same time, in order to judge whether there is a loss of model performance after grouping, the experimental results on raw undivided data are also counted.Table 3 shows the average AUC values of PSO-EVFFS under differentMvalues.The‘groups’ in Table 3 equals to ‘participants’.

As can be seen from Table 3 that ①for all 10 datasets,the classification performance of the algorithm decreases with the increase of the number of participants.Taking the Yale64 dataset as an example,the AUC value is 0.7974 with raw undivided data and is 0.7969,0.7945 and 0.7916,respectively,when the dataset isassigned to two,three and five participants; ②however,as the number of participants increases,the performance of the algorithm declines only to a small degree,sometimes close to 0.This is mainly because the SecureBoost framework itself is a lossless framework [24].Taking the Yale64 dataset as an example, the maximum error between raw undivided data and five-grouped dataset is only 0.18%.For the Coil dataset,the AUC values are all 0.9919 when it is assigned to two and three participants.Therefore,the number of participants has no obvious effect on the performance of the algorithm.

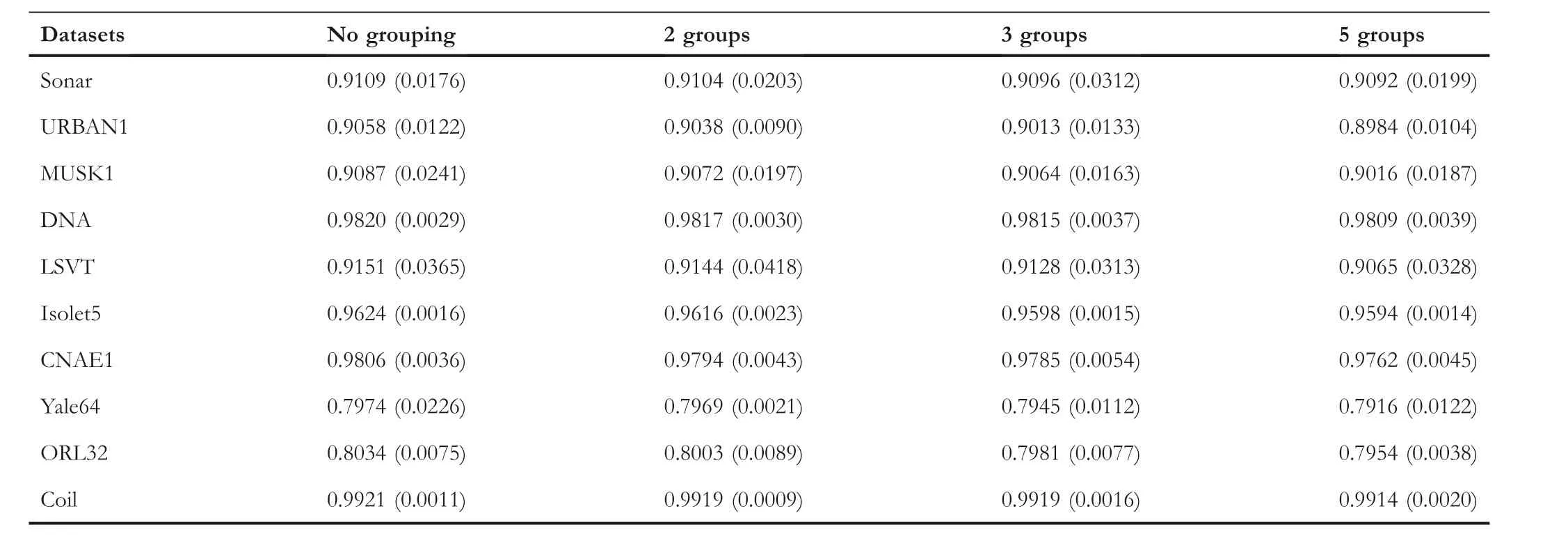
T A B L E 3 The average AUC values obtained by the proposed algorithm under different number of participants

Furthermore,we discuss the running time of the algorithm when using different numbers of participants.The average running time of the algorithm for 30 times is calculated for all the four cases, that is, the raw undivided data, two, three and five participants, respectively, as shown in Figure 5.

As can be seen from Figure 5,for all 10 datasets,the running time of the algorithm on the raw undivided data is the fastest.This is because the XGBoost model is only used for FS in the case, and there is no information interaction between participants.The running time of the algorithm for the case of two participants is faster than that of three and five participants.Taking the Yale64 dataset as an example, its running time is 4532.59,4720.90 and 4987.71 s when having two,three and five participants, respectively.This is because the communication cost between participants increases as the number of participants increases.Overall, the proposed PSO-EVFFS algorithm can obtain a nearly lossless FS model for multiple participants on vertical distributed data.However,the increase of the number of participants will increase the running time of the algorithm.

5.5 | Effectiveness analysis of the swarm initialisation strategy

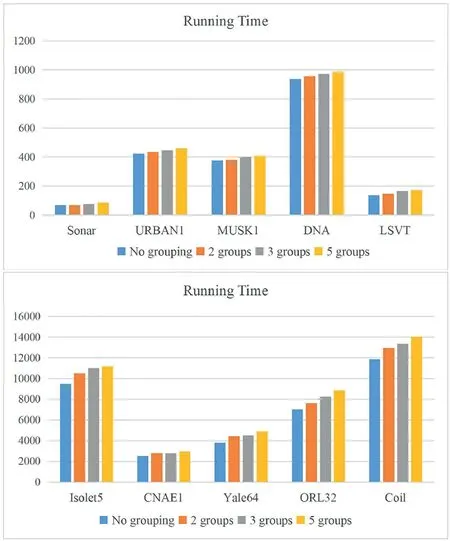
F I G U R E 5 The average running time of the proposed algorithm under different number of participants (Unit: s)

In order to comprehensively demonstrate the effectiveness of the three initialisation strategies,besides AUC,classification accuracy (ACC) and F1-score indicators are also counted in this section.Without loss of generality, this experiment considers the case with three participants.Table 4 shows the average F1-Score, ACC and AUC values obtained by PSOEVFFS under three initialisation strategies.

As can be seen from Table 4 that ①for all 10 datasets,the three indicator values of the FIIS strategy proposed in this paper are significantly better than the RIS strategy.Taking the MUSK1 dataset as an example,the F1-score,ACC and AUC values obtained by FIIS are 0.8390,0.8415 and 0.9064,respectively,while the three indicator values obtained by RIS are 0.8133, 0.8146 and 0.8782,respectively.This is mainly because FIIS introduces the feature importance to guide the initial particle to select good features;②for all 9 datasets except Sonar,three indicator values of FIIS are better than that of the PIS strategy.Taking the Yale64 dataset as an example,the F1-score,ACC and AUC values obtained by FIIS are 0.7123,0.9483 and 0.7945,respectively,while the three indicators obtained by PIS are 0.6810, 0.9320 and 0.7780, respectively.This is mainly due to the segmented initialisation strategy adopted by the FIIS strategy.Compared with the PIS strategy that entirely relies on the feature importance to generate particle,FIIS only performs the probabilistic selection mechanism for top-ranked and bottom-ranked features and still uses the random method to generate their initial positions for those remaining intermediate middle.This can not only ensure the convergence of swarm but also guarantee its diversity.

Furthermore, in order to more intuitively display the evolution process of PSO-EVFFS under the three strategies,Figure 6 shows the AUC evolution curve of the algorithm when iterating 20 times.It can be seen that in most cases, the AUC curve value of FIIS is higher than that of RIS and PIS.In particular, for all the 10 datasets, the maximum AUC vaues obtained by FIIS are greater than that of RIS and PIS.Specifically,for most of datasets,RIS has a faster convergence rate,but it is more likely to fall into premature stagnation.Due to the relatively poor diversity of the initial swarm generated by PIS, its ability to jump out of the local optimum is inferior to that of FIIS proposed in this paper.For most of datasets, the maximum AUC values obtained by FIIS are higher than that obtained by PIS.

5.6 | Comparative results and analyses

In this section, three typical vertical-federated learning algorithms (i.e.SecureBoost, VFLR and VFDNN) are selected as the comparison algorithms to verify the performance of the proposed algorithm.

(1) Comparison of statistical results

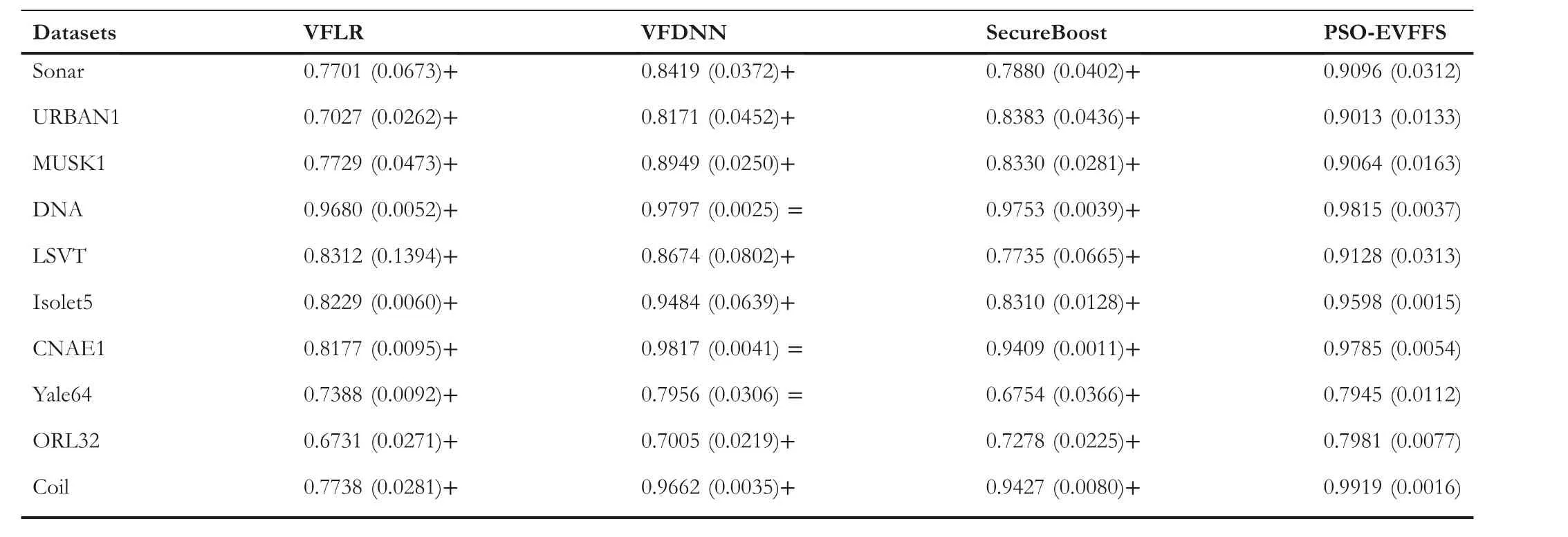
In order to make a fair comparison, for each dataset, the four algorithms use the same data division results and the data subsets held by participants are not visible to each other.Furthermore, t-test with a confidence of 0.05 is usedto evaluate the significant difference between two algorithms.Here, ‘+’ indicated that the result of PSO-EVFFS is significantly better than that of the comparison algorithm, ‘-’indicated that the result of the comparison algorithm is significantly better than that of PSO-EVFFS, and ‘=’ showed no significant difference between the two algorithms.Without losing generality, this experiment only considers the case with 3 participants.Table 5 shows the average AUC values obtained by PSO-EVFFS and the three comparison algorithms.

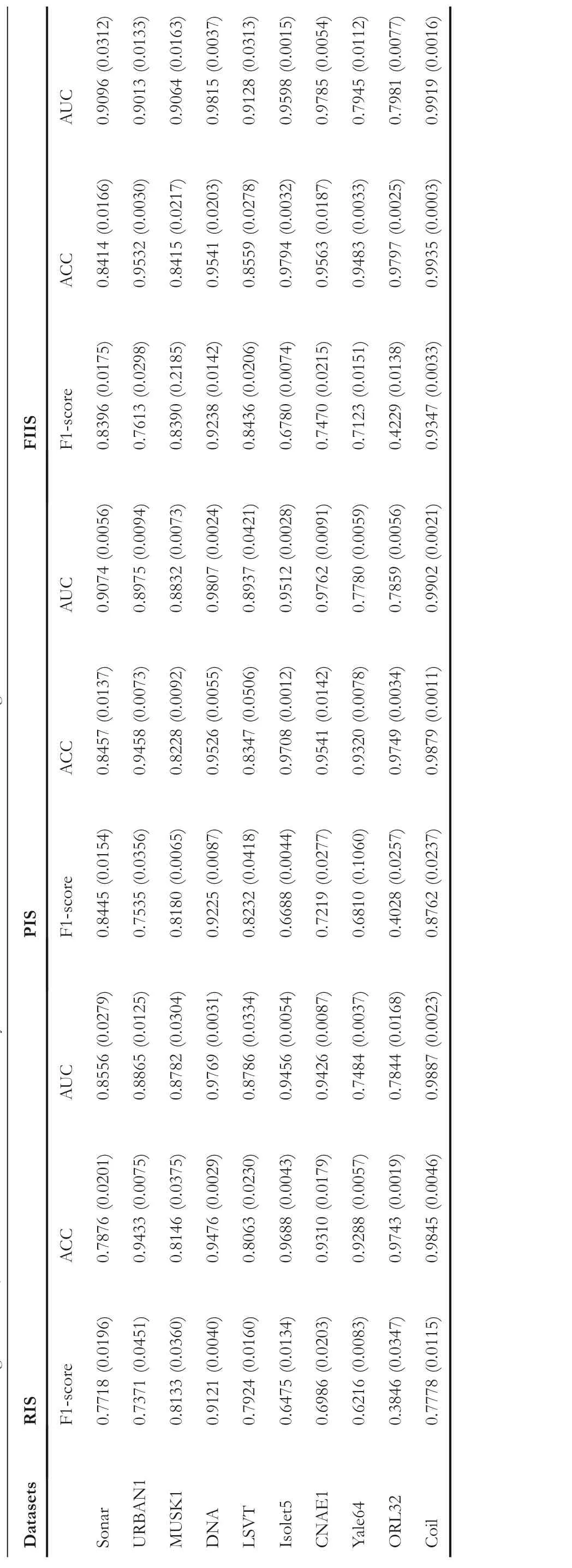
T A B L E 4 The average F1-Score, ACC and AUC values obtained by PSO-EVFFS under three initialisation strategies

F I G U R E 6 The evolution curves of AUC obtained by PSO-EVFFS under three initialisation strategies

It can be seen from Table 5 that (1) the classification performance of PSO-EVFFS is significantly better than VFLR and SecureBoost.Take the MUSK1 dataset as an example; the AUC value obtained by PSO-EVFFS is 0.9064,while the AUC value obtained by VFLR and SecureBoost is 0.7729 and 0.8330, respectively.The main reason is that, on the one hand, although SecureBoost can rank the importance of features, it cannot remove redundant features between participants.These features will be bound to affect the classification effect of the model.On the other hand, in theVFLR framework, the logistic regression model is based on the assumption that features and labels have a certain linear relationship.When the relationship between feature and label is non-linear, the effect becomes unsatisfactory.On the contrary, PSO-EVFFS can not only maintain the basic framework of SecureBoost but also remove redundant features using evolutionary FS, ensuring the optimality of model hyper-parameters and feature subsets.

T A B L E 5 The average AUC values (standard deviation) obtained by PSO-EVFFS and the three comparison algorithms

(2) Although the classification performance of PSOEVFFS is similar to that of VFDNN for the three data sets,DNA, CNAE1 and Yale64, the classification performance of PSO-EVFFS is better than that of VFDNN for the other 7 datasets.For the four datasets with a large number of samples,namely DNA, Isolet5, CNAE1 and Coil, the AUC values of VFDNN are all above 94%.However,the AUC values on the remaining 6 datasets with small samples are all lower than 90%.Compared with VFDNN, PSO-EVFFS has an AUC value lower than 90% only on two datasets.

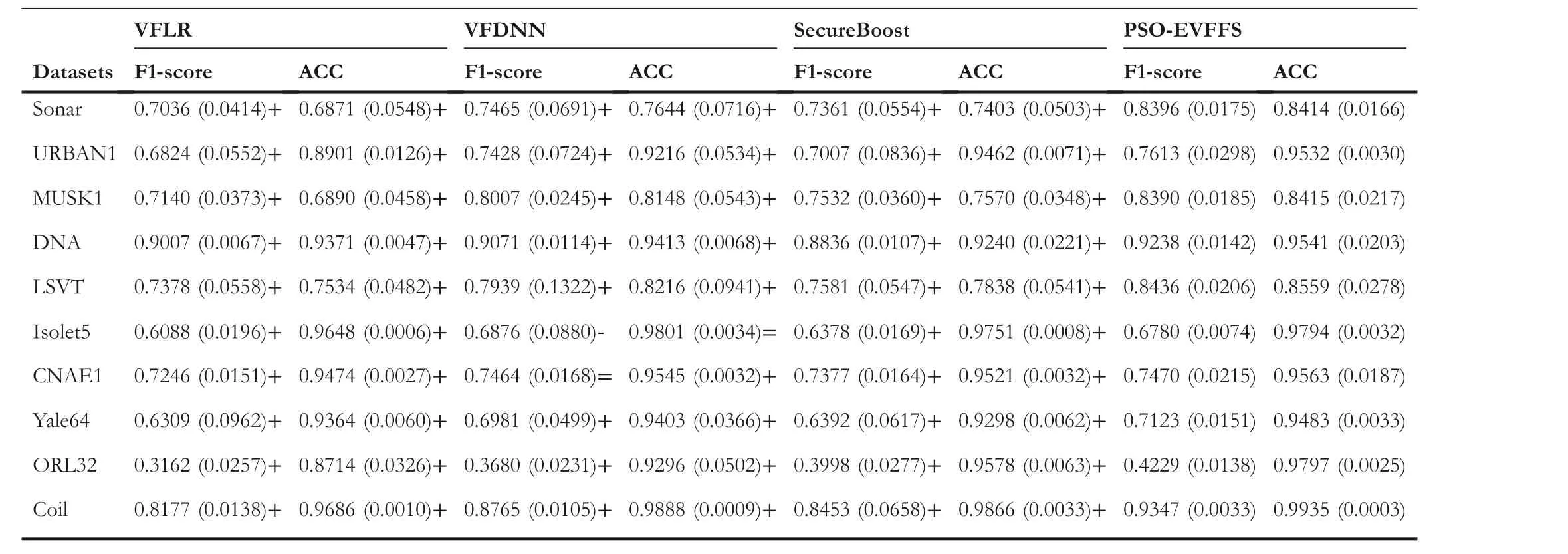
Furthermore, Table 6 shows the average F1-score and ACC values obtained by PSO-EVFFS and the three comparison algorithms.Without losing its generality, the experiment considered the case involving three participants.We can see that ①for all the 10 datasets,similar to AUC,the F1-score and ACC values of PSO-EVFFS are significantly superior to those of VFLR and SecureBoost.Taking the MUSK1 dataset as an example, F1-score and ACC values obtained by PSO-EVFFS are 0.8390 and 0.8415, respectively, while the two performance indicator values obtained by VFLR and SecureBoost are 0.7140 and 0.6890, 0.7523 and 0.7570, respectively; ②PSOEVFFS has better classification performance than VFDNN for 9 datasets except Isolet5.For the dataset Isolet5, the classification performance of PSO-EVFFS is inferior to that of VFDNN.This is mainly because more training samples are more conducive to the training of learning algorithm.

To sum up, the proposed PSO-EVFFS algorithm can achieve better classification performance under the premise of protecting data privacy in the scenario of vertical distribution of datasets, compared with the three typical vertical-federated learning algorithms, SecureBoost, VFLR and VFDNN.

(2) Significance analysis

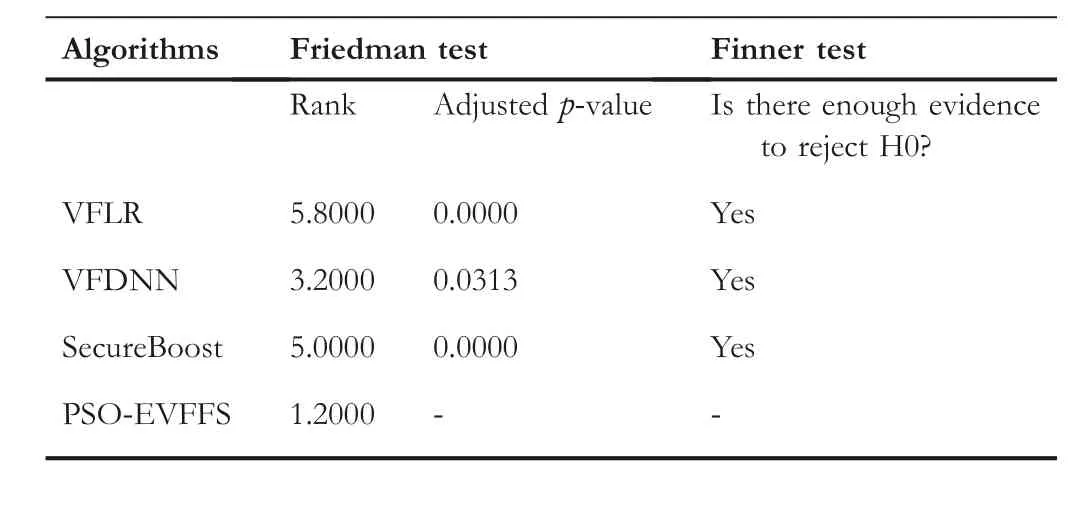
As the results obtained by an algorithm may not conform to normal distribution, the Friedman test [57, 58]with a significance level of 0.05 and the Finner test [59] with an alpha value of 0.05 are used in this section to verify whether there is significant difference between algorithms.Taking the AUC values as an example, Table 7 shows the statistical results of the proposed PSO-EVFFS and the three comparison algorithms.The smaller thepvalue of an algorithm is, the higher the confidence level of the algorithm is better than other algorithms.The smaller the ranking value of an algorithm, the better the performance of the algorithm on all datasets.It can be seen from Table 7 that PSOEVFFS has the smallest ranking value and its classification performance is significantly better than the three comparison algorithms.

6 | CONCLUSIONS

In this paper, an embedded vertical-federated FS algorithm based on particle swarm optimisation (PSO-EVFFS) was proposed to solve the privacy protection FS problem with vertical distributed data.By incorporating an improved evolutionary FS technology into SecureBoost framework, the proposed algorithm achieved better classification performance than the traditional SecureBoost framework.The designed integrated ranking strategy of feature importance in the first stage obviously reduced the search space of subsequent PSO algorithm.The mixed particle encoding strategy proposed in the second stage ensures that PSO-EVFFS obtained the optimal hyper-parameters of XGBoost tree model and good feature subsets simultaneously.The designed swarm initialisation strategy guided by feature importance significantly improved the quality of the initial swarm.The proposed PSOEVFFS algorithm was applied to 10 test datasets and compared with 3 typical vertical-federated learning algorithms.The results show that PSO-EVFFS can significantly improvethe classification performance of feature subset jointly selected by multiple participants while fully protecting data privacy and find a better set of model hyperparameters for SecureBoost.

T A B L E 6 The average F1-score and ACC values obtained by PSO-EVFFS and the three comparison algorithms

T A B L E 7 Results of Friedman and Finner test obtained by PSOEVFFS and the three comparison algorithms

Although the proposed algorithm successfully solves the privacy protection FS problem with vertical distributed data,it still has a relatively long running time, similar to other evolutionary FS algorithms,especially for high-dimensional datasets.Therefore,how to improve the running speed of the algorithm is a key content to be considered in the future.In addition,applying the proposed algorithm to practical problems is another content to be considered in the future.

ACKNOWLEDGEMENTS

This work was jointly supported by the two funding sources:Scientific Innovation 2030 Major Project for New Generation of AI, Ministry of Science and Technology of the Peoples Republic of China(2020AAA0107300);National Natural Science Foundation of China(62133015).

CONFLICT OF INTEREST

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are available on request from the corresponding author.The data are not publicly available due to privacy or ethical restrictions.

ORCID

Yong Zhanghttps://orcid.org/0000-0003-0026-8181