Overlapping community‐based particle swarm optimization algorithm for influence maximization in social networks
2023-12-01LeiZhangYutongLiuHaipengYangFanChengQiLiuXingyiZhang
Lei Zhang| Yutong Liu | Haipeng Yang | Fan Cheng| Qi Liu |Xingyi Zhang
1Information Materials and Intelligent Sensing Laboratory of Anhui Province,Key Laboratory of Intelligent Computing and Signal Processing of Ministry of Education,School of Computer Science and Technology,Anhui University,Hefei, China
2School of Computer Science and Technology,University of Science and Technology of China, Hefei, China
Abstract Influence maximization, whose aim is to maximise the expected number of influenced nodes by selecting a seed set of k influential nodes from a social network, has many applications such as goods advertising and rumour suppression.Among the existing influence maximization methods,the community-based ones can achieve a good balance between effectiveness and efficiency.However, this kind of algorithm usually utilise the network community structures by viewing each node as a non-overlapping node.In fact,many nodes in social networks are overlapping ones, which play more important role in influence spreading.To this end, an overlapping community-based particle swarm optimization algorithm named OCPSO for influence maximization in social networks,which can make full use of overlapping nodes, non-overlapping nodes, and their interactive information is proposed.Specifically, an overlapping community detection algorithm is used to obtain the information of overlapping community structures, based on which three novel evolutionary strategies, such as initialisation, mutation, and local search are designed in OCPSO for better finding influential nodes.Experimental results in terms of influence spread and running time on nine real-world social networks demonstrate that the proposed OCPSO is competitive and promising comparing to several state-of-the-arts(e.g.CGA, CMA-IM, CIM, CDH-SHRINK, CNCG, and CFIN).
K E Y W O R D S computational intelligence, data mining, social network
1 | INTRODUCTION
Recent years has witnessed the rapid development of social networks such as Facebook and Twitter, and social network analysis has become a hot spot research which includes many research fields,for example,community detection[1],network embedding [2], user behaviour analysis [3], social network emotion analysis [4], network vulnerability analysis [5], and so on.Among them,influence maximization[6]is to mineknodes to maximise the influence spread under a specific information diffusion model, such as Independent Cascade Model [7] and Linear Threshold Model [8].Influence maximization can be traced back to the study of‘viral marketing’and‘word of mouth effect’ [9] that makes information rapidly spread among the public, which has a very important practical application in marketing,advertising,rumour suppression and so on.
The problem of social influence maximization was firstly proposed by Dominigos and Richardson [6].Afterwards,Kempe et al.have proved the influence maximization problem was NP-hard, and proposed a hill-climbing greedy algorithm[10] to obtain approximate solution.However, this greedy algorithm needs to utilise multiple Monte-Carlo simulations to estimate the influence spread of nodes, so it has a high computational complexity and is not suitable for large-scale social networks.Therefore, various strategies were proposed to improve the efficiency of the algorithms [11–21],which are mainly considered from two aspects.The first aspect is to decrease the number of Monte-Carlo simulations.For example,Leskovec et al.[11]proposed CELF algorithm that utilised the submodular property of influence spread to reduce the number of Monte-Carlo simulations.Based on the similar idea, Goyal et al.[12] proposed CELF++ algorithm, which can further reduce the number of Monte-Carlo simulations by exploiting submodularity.However, the efficiency of these algorithms is still not very high.To this end, some researchers focussed on improving the efficiency from the aspect of designing heuristic algorithms.For example,Chen et al.proposed several heuristic methods such as degree discount[13]and MIP[14],which can greatly improve the efficiency.Recently,Bucur et al.proposed to utilise the surrogate model to approximate the evaluation of influence spread,which can achieve good efficiency[15].
Besides the above greedy or heuristic algorithms,community-based algorithms [22–34] have also shown their promising performance in solving the social influence maximization problem, which can achieve a good balance between effectiveness and efficiency by utilising the attributes of community structures.These community-based algorithms usually consist of the following three stages: (1) detecting community structures by using a community detection algorithm; (2) utilising the detected community structures to generate candidate set of nodes; (3) selecting seed nodes from the obtained candidate set.It can be found that this kind of algorithms take advantage of the attributes of community structures that nodes are densely connected in same community while edges are sparse between communities [35].Based on these community structures, the influential nodes can be easily found, which guarantees the effectiveness of community-based algorithms.At the same time, the idea of divide-and-conquer embodied in community-based algorithms can narrow the search space from the whole network to each community, which guarantees the efficiency of these algorithms.
Despite that community-based algorithms mentioned above have shown their competitiveness in obtaining the influential seed nodes with a good computational time, most of these algorithms simply regarded each node as a non-overlapping one,and used the information of non-overlapping communities obtained by a non-overlapping community detection algorithm to find top-kinfluential nodes.In real social network applications,many nodes should be regarded as overlapping ones rather than non-overlapping ones.For example, in the collaboration network,each author is regarded as one node,and the co-author relationship between two authors is regarded as an edge.Obviously,most of authors in this collaboration network usually belong to multiple communities such as Data mining and Deep learning.In fact, the nodes belonging to multiple social communities are more likely to influence more people in social networks[36].
Let us take the network shown in Figure 1 as an example.From Figure 1a, we can see that the network containing 14 nodes can be divided into two communities(Community 1{1,2,3,4,5,6,7,8}and Community 2{9,10,11,12,13,14})by a non-overlapping community detection method named LPA[37].Suppose the number of selected seed nodes is set to 3(i.e.k=3), the three yellow nodes{1,2,11} are the final selected seed nodes obtained by one representative community-based algorithm named CGA [22].Note that CGA uses LPA to get non-overlapping community structure, which neglects the overlapping information.In order to fully use the overlapping information, an overlapping community detection algorithm can be adopted to obtain the overlapping community structure firstly.From Figure 1b, it can be found that the network is divided into two overlapping communities(Community 1{1,2,3,4,5,6,7,8}and Community 2{8,9,10,11,12,13,14})by an overlapping community detection method named SLPA[38](a variant of LPA),where node 8 is an overlapping node.Note that the importance of overlapping nodes is fully considered in the proposed algorithm OCPSO, the two yellow non-overlapping nodes {1, 11} and one overlapping red node {8} are the final selected seed nodes.Then, in order to measure the quality of these algorithms,we adopt a popular method which calculates the influence spread of the ultimate seed set of each algorithm by running Monte-Carlo simulation for 10,000 times under the IC Model [7].Finally, we can get the seed {1, 8, 11} with the influence of 7 and the seed{1,2,11}with the influence of 6.We can see that the seed{1,8,11}is better than{1,2,11},since the node 8 is an overlapping one with a large probability of influencing another community, although the degree of node 2 is slightly larger than that of node 8.
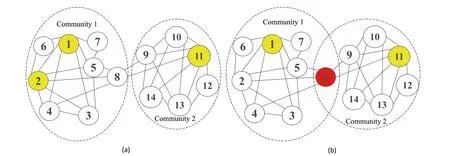
F I G U R E 1 (a) Two non-overlapping community structures obtained by a non-overlapping community detection method named LPA [37], where three nodes {1, 2, 11} marked in yellow are the selected seed nodes by one representative community-based algorithm named CGA [22] (suppose k = 3).(b) Two overlapping community structures obtained by an overlapping community detection method named SLPA [38], where two non-overlapping nodes {1, 11}marked in yellow and one overlapping node{8}marked in red are the selected seed nodes obtained by the proposed community-based algorithm overlapping community-based particle swarm optimization (OCPSO) where the importance of overlapping nodes is fully considered.
To this end, in this paper, we propose an overlapping community-based particle swarm optimization algorithm called OCPSO for influence maximization in social networks.The main idea is to separate overlapping nodes and non-overlapping nodes and measure their importance with different criteria to avoid ignoring the influential overlapping nodes in communitybased algorithms.The whole framework of OCPSO mainly consists of three steps.Firstly, an overlapping community detection algorithm (e.g.SLPA [38]) is used to detect overlapping nodes and their community structures.Then,two kinds of candidate sets including overlapping candidate nodes and non-overlapping candidate nodes are generated based on the selected important communities.Finally, a popular framework(e.g.local particle swarm optimization (LPSO) [39]) with the proposed evolutionary strategies by fully utilising the structural information of overlapping communities is used to search for top-kinfluential nodes.The main contributions of this paper are summarised as follows:
• A novel overlapping community-based particle swarm optimization algorithm called OCPSO is proposed for influence maximization, where overlapping nodes, nonoverlapping nodes and their interactive information are fully utilised to find the set of influential nodes.
• By fully utilising the overlapping community structure information, three novel evolutionary strategies (i.e.initialisation, mutation and local search) are designed, which can be used in OCPSO to greatly accelerate the convergence and improve the performance of the algorithm.
• Experimental results on nine real-world social networks with different characteristics show that the proposed OCPSO is a promising method for social influence maximization.In other words, OCPSO by fully utilising the overlapping characteristic of nodes can get a better balance between influence spread and computational efficiency.
The rest of this paper is organised as follows: Section 2 introduces some preliminaries and reviews related works.Section 3 presents the proposed OCPSO algorithm in detail.Experimental results and analysis of the proposed algorithm on nine real-world social networks are shown in Section 4.Finally, we conclude this paper and give the future work in Section 5.
2 | PRELIMINARIES AND RELATED WORK
In this section, we first introduce some preliminaries about influence maximization, including the problem formulation,information diffusion model and evaluation function.Next,we review the related works by focussing on community-based algorithms for influence maximization.
2.1 | Influence maximization problem
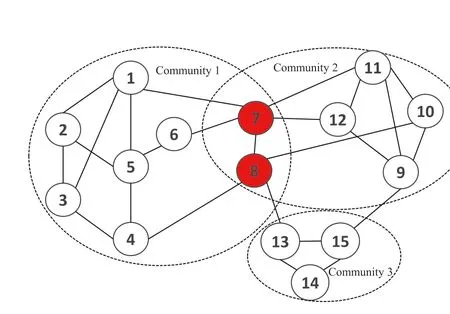
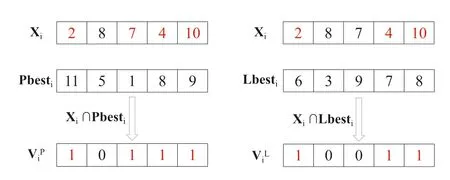
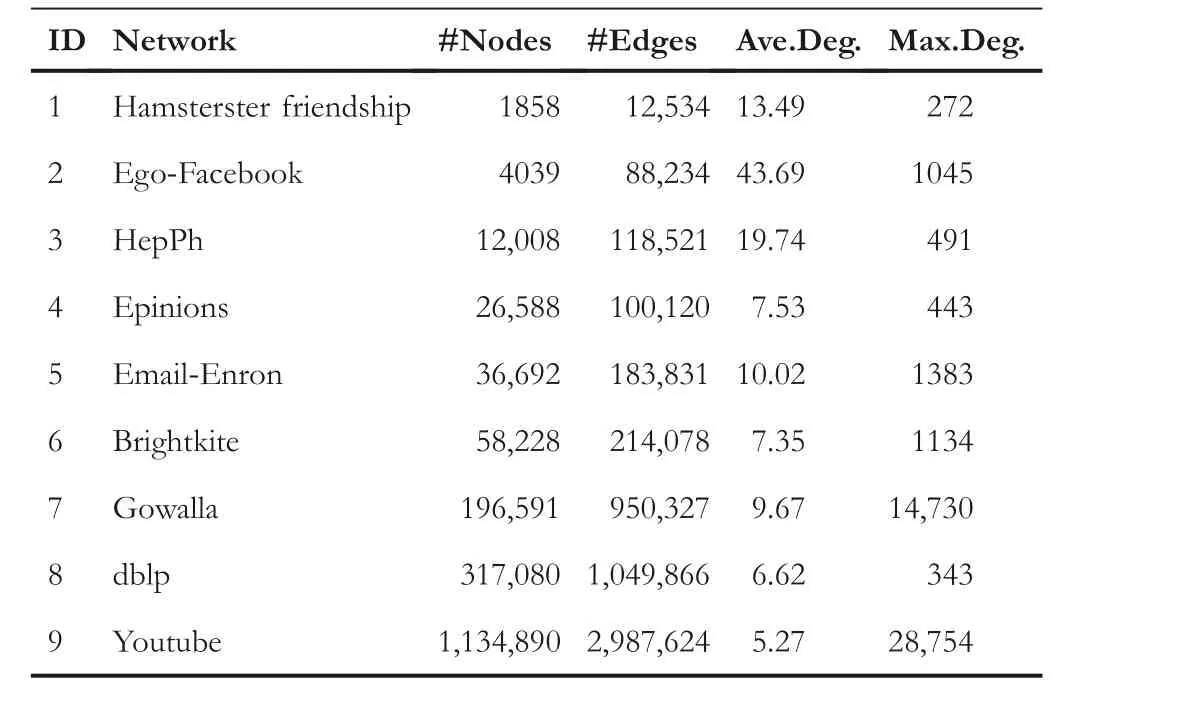
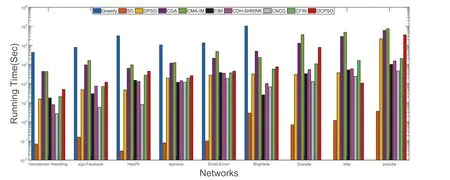
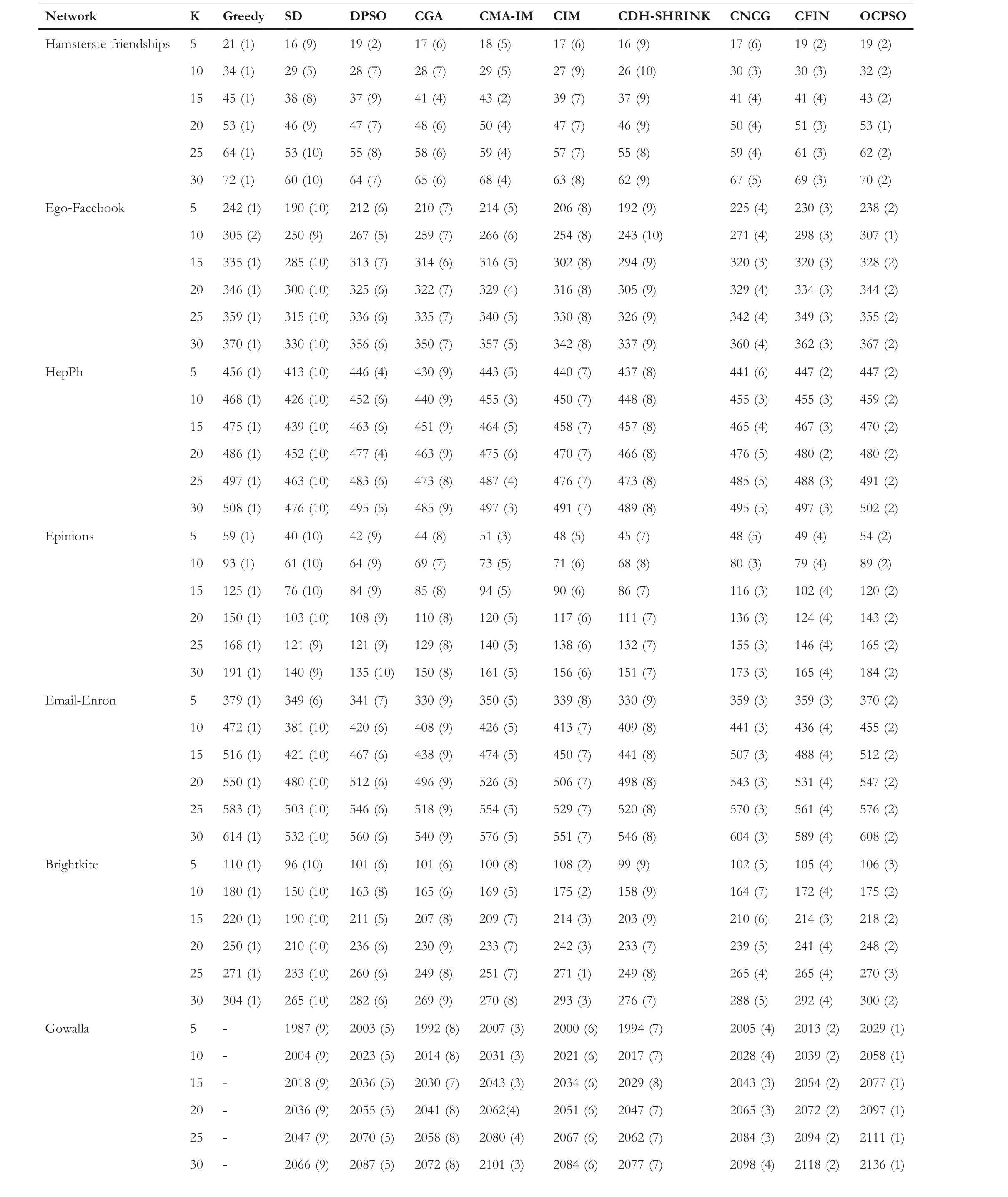
LetG= (V,E) be an undirected and unweighted graph of a social network, in whichVdenotes the node set (i.e.a set of users)andErepresents the edge set(i.e.relationships between users)in social network.Given a positive integer 0 Note that the activation order given a node with multiple newly activated is ascending order according to each node's label. 2.1.1 | Independent cascade model In this paper,we adopt the IC model to estimate the influence spread of seed nodes, which has been widely used in previous works [10–13, 40].In the IC model, the state of nodes is divided intoactiveorinactive.The inactive nodes may be switched into the active nodes, but not vice versa.More specifically, when a node is activated, it will try to activate its inactive neighbour nodes.However, these activation attempts are mutually independent and only made once.The information diffusion process is described as follows: • To begin with,the initial set of active nodesSare given andS0=S,Stdenotes the set of nodes that are activated by previous activated setSt-1at stept. • At stept, each node inSt-1attempts to activate its inactive neighbour nodes with the probabilityp.If one node is activated, it will be joined inSt. • The above process continues until no new node is activated,namelySt= ∅.Let VSbe the set of nodes activated byS,then VS=⋃ti=0Si. 2.1.2 | Evaluation function The influence spread is usually computed by Monte-Carlo simulation.However, the larger the social network is, the more time-consuming Monte-Carlo simulation is [10].To this end, an approximate evaluation function (EDV) that was proposed by Jiang et al.[41] to efficiently estimate the influence spread of the seed set.The formula is defined in the following. In recent years, many community-based algorithms have been proposed to solve the influence maximization problem in social networks. For example, Cao et al.[22] proposed a community-based method called OASNET for solving the problem of influence maximization in social networks.In OASNET, the influence maximization problem was transformed to an optimal resource allocation problem.Then,nodes allocated for each community were selected as candidate nodes according to a dynamic programing method.Finally,seed nodes were selected from candidate nodes by using a greedy strategy.In the same year, Wang et al.[23]proposed a community-based algorithm called CGA for influence maximization on mobile social network,which also utilised greedy strategy and dynamic programing to mine the influential nodes.Compared with OASNET,CGA did not need to allocate the number of seed nodes in each community in advance,and directly selected seed node by maximising current marginal gain from corresponding community one by one until the number of seed nodes were selected.Compared with other algorithms such as greedy and heuristic ones,the experimental results have shown that community-based algorithms can achieve a good balance between effectiveness and efficiency. Since then, more community-based algorithms have been developed.For example, Song et al.proposed a parallelised community-based algorithm [26] by considering the influence spread among communities to further improve the performance of the algorithm.Chen et al.[27] proposed a community-based algorithm called CIM for influence maximization, in which the heat diffusion model was used to estimate the influence spread.In CIM, a hierarchical community detection algorithm called H_Clustering was firstly proposed to detect community structures to obtain the influential hub nodes.Then,two optimization strategies,quota-allocation and insignificant pruning, were proposed to enhance the influence spread as well as speed up the execution time of CIM.In addition, Rahimkhani et al.[42] proposed a community-based algorithm called ComPath for influence maximization.Firstly,it detected community structures and took communities as nodes to form a new network.Then it selected the most influential communities according to betweenness centrality.Next, a number of nodes were selected based on degree to generate candidate set from the most influential communities.Finally, top-kinfluential nodes were selected from candidate on the basis of the paths existing in the network.However,this algorithm ignored certain communities that are large but have few connections with other communities. After that, Gong et al.[28] proposed an efficient memetic algorithm named CMA-IM to solve the influence maximization problem by optimising the 2-hop influence spread.Firstly, it detected community structures and generated candidate set of nodes.Then,a memetic evolutionary framework with the proposed strategies such as problem-specific population initialisation and similarity-based local search were suggested to search for the ultimate seed set from candidate set of nodes.Shang et al.[29]proposed a new community-based algorithm called CoFIM to solve influence maximization problem.This algorithm contained two steps: node expansion and intra-community propagation.In the first step, it expanded seed nodes between communities.In the second step,they assumed all communities were isolated with each other and spread the influence within communities.Thereafter, Huang et al.[43] presented a community-based algorithm named CTIM to improve the greedy algorithm.The algorithm initially used the comprehensive latent variable model to obtain favourite topics and distribution of the community members from each user.Then,it used favourite topics to gain influence power in each community.Next,it chosekinfluential nodes using the divide-and-conquer algorithm.Recently,Khomami et al.[44]designed an algorithm called Community Finding Influential Node (CFIN) with the purpose of selecting optimal users on the basis of the community structures,which in turn maximised the influence spread in the networks.The CFIN algorithm was split into two stages:seed selection and local community spreading.In the first stage,seed nodes were extracted via community detection algorithm.Here, with the objective of reducing the computational complexity involved in selecting seed node, meaningful communities were obtained.Next, the influence spread inside communities that were independent of each other.In this stage,the final seed nodes entered to distributed the local spreading by the use of a simple path inside communities.In addition,some other recent community-based algorithms can be found in refs.[32–34]. Despite the above community-based algorithms have achieved good results in terms of both influence spread and computational efficiency, however, most of them utilise the network community structures by viewing each node as a nonoverlapping node.In fact, a considerable number of nodes in social networks can be overlapping ones (i.e.the node belonging to multiple communities), which are more likely to spread the influence in social networks[36,45].In other words,the existing community-based algorithms ignore fully utilising the influential overlapping nodes in the network.To the best of our knowledge,there is only a few work on designing influence maximization algorithms by exploiting overlapping community structures.Chen et al.[24] preliminarily proposed the CDHSHRINK by utilising overlapping community structures to solve the influence maximization problem.Specifically, CDHSHRINK mainly consists of two phases: partition phase and selection phase.In the first partition phase, a hierarchical network clustering algorithm was utilised to not only discover communities but also identify hubs(i.e.overlapping nodes)and outliers.In the second section phase,in each round,a potential pool was constructed by selecting a part of high degree nodes in current largest community,from which a seed node was selected by comparing the priority of different nodes.The second phase continued untilk-seeds were selected.The experimental results have demonstrated the effectiveness of the algorithm.However,by taking a close look at this algorithm,it can be found that in CDH-SHRINK the importance of overlapping nodes is viewed same as that of the non-overlapping ones,which does not make full use of the overlapping nodes.To this end,recently,both[46,47]further considered the importance of overlapping structures and proposed greedy algorithms to select finalk-seeds.Specifically,Li et al.[46]proposed a greedy algorithm named DEIM for finding thekinfluential nodes from a candidate seed set,which was constructed by selecting nodes with the largest degree in each community and the overlapping nodes located in six or more communities at the same time.Wang et al.[47]proposed another greedy algorithm named CNCG to selectkseeds based on a node coverage gain measure,which was used to evaluate the influence of each node locally within its belonging communities.The experimental results on different social networks have demonstrated the supper performance of DEIM and CNCG.Despite the greedy algorithms can perform well in many cases,they could be trapped in local optimum[48]. To this end, this paper exploits evolutionary algorithms(EAs)which have global search capabilities to escape the local optimum in influence maximization problem.Specifically, we propose an overlapping community-based particle swarm optimization algorithm named OCPSO for influence maximization, where the overlapping nodes, non-overlapping nodes and their interactive information are fully utilised in the process of optimization.The main idea of OCPSO is to separate overlapping nodes and non-overlapping nodes and measure their importance with different criteria, with which novel evolutionary strategies such as initialisation,mutation and local search are suggested in OCPSO to find the better set of influential nodes.In Section 4, we will verify the competitive performance of OCPSOon nine real-world social networks with different characteristics in terms of both influence spread and computational efficiency, comparing to several state-ofthe-art influence maximization algorithms. In this section, we present a detailed description of the proposed overlapping community-based particle swarm optimization algorithm OCPSO for influence maximization. The framework of the proposed OCPSO is shown in Figure 2,which consists of three main steps.In the first step, an overlapping community detection algorithm named SLPA [38] is used to get overlapping community structures C = {C1,C2,…,CM}(Mis the number of detected communities),based on which the overlapping nodes,non-overlapping nodes and their structural information are easily obtained.In the second step,different from the existing community-based influence maximization methods, the candidate set of nodes is divided into two sub-sets: the candidate set of overlapping nodesCandoand the candidate set of non-overlapping nodesCandn.Noting that not every community is important enough to select seed nodes.To improve the computational efficiency,only a part of significant communities are selected according to their numbers of nodes in communities, which is popularly suggested in existing community-based algorithms such as refs.[27, 44].Thus, the topN( F I G U R E 2 Overall framework of overlapping community-based particle swarm optimization algorithm. Algorithm 1 Framework of OCPSO algorithm? From the above description of Algorithm 1, it can be found that the proposed initialisation strategy, mutation strategy and local search strategy by fully utilising overlapping community structures are three important parts in OCPSO.In the following, we will illustrate them in detail. F I G U R E 3 A illustrative network with overlapping community structures detected, where there are three communities labelled asCommunity 1, 2, 3 and two overlapping nodes marked in red. ?Algorithm 2 Initialisation (Cando, Candn, pop, k) Note that we adopt a popular evolutionary framework named LPSO [39] to find the influential seed set.In LPSO, each particle has a position vector and velocity vector.Let Xi=(xi1,xi2, …,xik) beith particle's position vector in particle swarm,wherexij∊Xirepresents one node in candidate set of nodes.Let Vi= (vi1,vi2, …,vik) beith particle's velocity vector,where eachvij∊{0,1}.At the beginning,V and X are all set to 0.In order to accelerate the convergence and improve the influence spread of the algorithm, we propose a novel diversified particle initialisation method by utilising overlapping and non-overlapping nodes to initialise the particle position vector. Before initialising the position vector of the particle swarm,we should determine the ratio of overlapping nodes and nonoverlapping nodes in each particle position vector.Letkoandknbe the number of overlapping nodes and non-overlapping nodes in the particle position vector respectively.Next, we suggest an allocation method to initialise the number of overlapping nodes and non-overlapping nodes, which is given in the following. where the term(|Cando|)/(|Cando|+|Candn|)is the ratio of overlapping nodes in significant communities andkis the sizeof the seed set.Noting thatkoandknare fixed at initialisation stage and will be adjusted adaptively in the evolution,which will be shown in Section 3.3.Thus, the task of particle position initialisation is how to selectkooverlapping nodes fromCandoandknnon-overlapping nodes fromCandn.In light of different characteristics of overlapping nodes and non-overlapping nodes, we adopt different strategies to select overlapping nodes and non-overlapping nodes for each particle. T A B L E 1 Notations used in this paper For selecting overlapping nodes,we suggest a metricOIto measure the influence importance of overlapping nodes,which is defined as follows: whereNB(u)=N(u)∪u,andN(u)={v|∃v∊V,(u,v)∊E}.Nodeuis the similar neighbour node ofvifSim(u,v) is no less than a minimal similarity thresholdmin_sim.Otherwise,nodeuis the dissimilar neighbour node ofvifSim(u,v) is larger thanmin_sim. For selecting non-overlapping nodes, the degree is considered as a fundamental metric for measuring node's influence.However, most of the nodes with higher degree maybe tend to gather in the same area, which easily leads to overlapping influence among nodes.In order to alleviate the overlapping influence and improve the diversity of the particle swarm, the selection of non-overlapping nodes starts by randomly select one nodeuof the top-2 largest degree nodes inCandn.Then,the nodeuand its similar neighbour nodes are removed fromCandn.This process iteratively operates untilknnodes are selected.IfCandn= ∅and the number of selected non-overlapping nodes (supposej) is not reached tokn, then the remaining nodes {vj+1,…,vkn} are randomly selected fromCandn.The whole process of initialisation is described in detail shown in Algorithm 2. Taking the network shown in Figure 3 as an example, whereCando={7,8}andCandn={1,2,3,4,5,6,9,10,11,12}.Suppose the size of the seed setkis set to 3.According to Equation (3), we can getko=「3*22+10⏋=1 andkn=3 - 1 = 2.Next, our task is to select one overlapping node fromCandoand two non-overlapping nodes fromCandn.To be specific, the overlapping node 7 is firstly selected fromCandosince it has the largest value ofOI.Then, for nonoverlapping nodes, suppose the first non-overlapping node 5 is randomly selected from the top-2 highest degree nodes {1,5} inCandn.According to Equation (5), the similar nodes of node 5 are {1, 2} , thus {1, 2, 5} should be removed fromCandn.Now the top-2 highest degree nodes inCandnare{9,11}.At this time,suppose the second non-overlapping node 9 is randomly selected from{9,11}.Finally,the particleXi={5,7, 9} is obtained by the proposed initialisation strategy. The main advantages of LPSO are that the optimised function does not need to meet too many constraints and its convergence is very fast.In addition,LPSO can also prevent particles fall into local optimum state in the evolutionary process.However,LPSO was proposed to solve the continuous optimization problem.Borrowed from the idea of applying PSO to solve discrete optimization problem [49].In this paper, we apply LPSO to solve the discrete influence maximization problem, where the particle velocity and position updating rules are designed for evolution.Specifically, the particle velocity updating rule forith particle's velocity vectorViis defined as follows: wherewis the inertia weight,c1,c2are two learning factors,andr1,r2are two random numbers between 0 and 1.Note thatPbestidenotes the historical optimal position of theith particle whileLbestidenotes the local optimal position in the neighbourhood ofith particle.The neighbourhood structure of particle in the ring topology is composed of particles adjacent to the current particle.In Equation (6), forith particle's position vectorXi=(xi1,xi2,…,xik),H(⋅)is a mapping function, which is defined as follows. A simple example for illustrating particle velocity updating is shown in Figure 4,where the position ofith particle is Xi=(2,8,7,4,10),Pbesti=(11,5,1,8,9)and Lbesti=(6,3,9,7,8).To begin with, we get the intersectionISthat the set of elements that are in common between the two vectors of Xiand Pbesti,and getIS={8}.Then these positions in VPicorresponding to the node in the intersectionISare set to 0,which denotes these nodes tend to be reserved.The other positions in VPiare set to 1,which denotes these nodes tend to be changed.Finally, we obtain VPi=(1,0,1,1,1).Similarly, VLi=(1,0,0,1,1) can be obtained.Assuming thatc1r1=0.8 andc2r2=1.5,then Vi=H(0.8* (1,0,1, 1,1)+1.5*(1, 0,0, 1,1))=H(2.3,0, 0.8,2.3,2.3)=(1,0,0,1,1). After updating the particle velocity, we need to utilise velocity vector to guide the update of position vector.To be specific, if the elementjin Viequals to 0, the corresponding elementxijin Xiwill keep unchanged.Conversely, if the elementjin Viequals to 1,the corresponding elementxijin Xiwill be replaced by other nodes.Formally,the particle position updating rule forith particle's position vector Xiis given in the following. whereRep(xij,Cando) is a function that can replace the elementxijwith one node inCandoXiwith the largestOI,whileRep(xij,Candn)is a function that can replace the elementxijwith one dissimilar node inCandnXiwhich has the largest degree.Noting that the two functions can guarantee that there is no repeated node in Xiafter the replacement. F I G U R E 4 The operator‘∩’is illustrated.{2,8,7,4,10}∩{11,5,1,8,9}={8}.Therefore,the corresponding position in of 8 in Xi are set to 0 and other positions are set to 1.That is, =(1,0,1,1,1).Similarly,=(1,0,0,1,1). Algorithm 3 Update Mutation(Cando,Candn,Xi,Vi)input: the set of overlapping candidate nodes Cando, the set of nonoverlapping candidate nodes Candn, the position vector of a particle Xi, the velocity vector of a particle Vi.output: X′i, V′i.1 Step1: Position and velocity vector update.2 V′i←update velocity vector by Equation (6);3 X′i←update position vector by Equation (8);4 Step2: Position vector mutation.5 X1i ←X′i;6 X2i ←X′i;7 na ←get one non-overlapping node with the largest degree in CandnX′i;8 nd ←get one overlapping node with the smallest OI in X′i;9 X1i←replace node nd with node na in X1i;10 na ←get one overlapping node with the largest OI in CandoX′i;11 nd ←get one non-overlapping node with the smallest degree in X′i;12 X2i←replace node nd with node na in X2i;13 X′i ←arg maxXi∊ X′i,X1i,X2i{ } EDV (Xi ){ }; Noting that,in Equation(3),we suggest a method to allocate the initial number of overlapping nodes and non-overlapping nodes for a particle position vector Xi, in order to further drive the particle to the promising regions,we propose a particle position mutation operator, which can dynamically adjust the ratio of overlapping nodes and non-overlapping nodes in the position vector Xiduring the evolution.To be specific, each particle Xihas an opportunity to adjust the corresponding number of overlapping nodes and non-overlapping nodes in each iteration process.There are two cases for mutation, one case is to replace one overlapping node with the smallestOIin Xiwith one non-overlapping node with the largest degree in(CandnXi).Then,we can get one new particle X1i.The other case is to replace one non-overlapping node with the smallest degree in Xiwith one overlapping node with the largestOIinCandoXi.Then,we can get another new particle X2i.Finally,we compare theEDVof the two newly generated particles X1iand X2iwith that of Xi,and retain the particle with the largestEDVamong the three particles as the final returned particle position vector.The whole process of update and mutation is shown in Algorithm 3 in detail. We take also the network shown in Figure 3 as an example,whereCando={7,8}andCandn={1,2,3,4,5,6,9,10,11,12}.Suppose one particle Xi={3,5,8,9},in which there exist one overlapping node{8}and three non-overlapping nodes{3,5,9}.In this example,there are two cases for mutation.The first case is that the overlapping node 8 in Xiis replaced with the? Algorithm 4 LocalSearch(Cando, Candn, C′, Xi)input: the set of overlapping candidate nodes Cando, the set of nonoverlapping candidate nodes Candn,the selected overlapping communities C′= C′1,C′2,…,C′N■, one particle position vector Xi.output: a new particle position vector X*i after local search operator.1 S = Xi;2 IS ←get the influenced node set activated by seed S by Monte-Carlo simulations;3 Step1: Add and remove operations for changing non-overlapping nodes in S while overlapping nodes are fixed.4 Ca ←arg minCi∊C′ |Ci ∩IS|■{ };5 Cd ←arg maxCj∊C′ |Cj ∩IS|■ ■;6 na ←arg maxu∊Candn∩(CaS)){EDV(S ∪{u})};7 nd ←arg maxv∊Candn∩(Cd ∩S)(() EDV (S∪{{ }{v})};8 S′ ←replace node nd with node na in S;9 Step2:Add and remove operations for changing overlapping nodes in S′ while non-overlapping nodes are fixed.10 na ←arg maxu∊CandoS′na( ) EDV S′∪{u}( )};11 nd ←arg maxv∊Cando∩S′{( ) EDV S′∪ {na }{v}()};12 X*i←replace node nd with node na in S′;{ In order to improve the convergence speed, we propose a novel local search strategy by using the information of overlapping nodes and non-overlapping nodes to improve the performance of elite particle in each iteration.The basic idea of this strategy is firstly to replace one non-overlapping node in seedSwith one inCandnwhile overlapping nodes are fixed in the first step, then replace one overlapping node in the newly updatedS′with one inCandowhile non-overlapping nodes are fixed in the second step.For each step, there are two main operations: ‘add operation’ and ‘removal operation’.The ‘add operation’adds one important node into the particle while the‘removal operation’ removes one unimportant node from the added particle.Algorithm 4 presents the main procedure of local search strategy, which mainly consists of two steps. To be specific,in the first step,we change non-overlapping nodes in seedSwhile overlapping nodes are fixed.Firstly, the influenced node set activated by seedSby Monte-Carlo simulations is obtained, denoted asI.Then, we intersect each communitywithISand obtain two communities: the communityCain Cwhich has the smallest size of the intersection,and the communityCdin C′which has the largest size of the intersection.It is intuitive to replace one node inCdwith one node inCa,which has a large probability of improving the final influence spread of seed nodes.Thus,in the‘add operation’,the nodenainCandn∩(CaS)with the largestEDVof (S∪{na}) is selected as the added one.Then, in the‘delete operation’, the nodendinCandn∩(Cd∩S) with the largestEDVof(S∪{na}{nd})is selected as the deleted one.Finally, the newly updatedS′can be obtained by replacing the nodendwith the nodenainS.In the second step, we change overlapping nodes in seedS′while non-overlapping nodes are fixed.Specifically, in the ‘add operation’, the nodenain (CandoS′) with the largestEDVof (S′∪{na}) is selected as the added node.Then, in the ‘delete operation’, the nodendin(Cando∩S′) with the largestEDVof (S′∪{na}{nd}) is selected as the deleted one.Finally, the newly updated X*iis obtained by replacing the nodendwith the nodenainS′. In this section, we give the time complexity and space complexity of the proposed OCPSO.According to the framework of the proposed algorithm,the time complexity includes three parts.The first part is the overlapping community detection algorithm SLPA.According to the original text [41],its time complexity isO(T×m), whereTis the number of iterations andmis the number of edges in social network.The second part is to obtain important communities from the detected communities for candidate set generation, its time complexity is actually the time complexity of sorting,which isO(M2)andMis the number of important communities.The third part is the particle swarm evolution, in which the time complexity of calculating the function value isO(k×pop×maxgen), the time complexity of the optimization process includes the time complexity of initialisationO(pop×k2), the time complexity of mutationO(k×pop×maxgen) and the time complexity of local searchO((k2 +q2) ×maxgen) (qis the number of nodes in important communities),thus the time complexity of the third part isO(k×(pop×maxgen+pop×k+pop×maxgen+k×maxgen) +q2 ×maxgen).Sincemaxgenis usually set topopandq2 ≫(2×k×pop+2×k2)in general, so it can be further simplified asO(pop×q2).In summary,the total time complexity of OCPSO isO(T×m+M2+pop×q2).In addition,the space complexity includes the space complexity of the found communitiesO(n) (nis the number of nodes in social network), the space complexity of candidate nodesO(q),the space complexity ofPbestandgbest O(2×k)and the space complexity of particle swarm vectorsO(2 ×k×pop), the total space complexity isO(n+q+ 2 ×k×(pop+1)).Sincen≫2×k×(pop+1)in general,the final space complexity can be further simplified asO(n+q). In this section,we verify the effectiveness and the efficiency of the proposed algorithm OCPSO by comparing it with nine existing baseline algorithms and three variants of OCPSO on nine real-world social networks.Specifically, we first introduce the experimental setup including datasets and comparison algorithms in Section 4.1, then present the experimental results and analysis in Section 4.2. 4.1.1 | Datasets In our experiments, we adopt nine static real-world social networks with different characteristics.To bespecific, Hamstersterfriendships,1http://konect.uni-koblenz.de/networks/petster-friendships-hamsterego-Facebook,2http://snap.stanford.edu/data/ego-Facebook.htmlBrightkite,3http://networkrepository.com/soc-brightkite.phpGowalla4http://snap.stanford.edu/data/loc-Gowalla.htmland youtube5http://snap.stanford.edu/data/com-Youtube.htmlare online social networks.HepPh6http://snap.stanford.edu/data/ca-HepPh.htmland dblp7http://snap.stanford.edu/data/com-DBLP.htmlarecollaboration networks.epinions8http://networkrepository.com/soc-epinions.phpis a trust network.Email-Enron9http://snap.stanford.edu/data/email-Enron.htmlis a communication network. T A B L E 2 Statistics of the nine real-world social networks Table 2 shows the statistical information of nine real-world social networks, where#Nodesdenotes the number of nodes while#Edgesrepresents the number of edges in the network,andAve.Deg.andMax.Deg.respectively represent the average degree and maximal degree of the network. 4.1.2 | Comparison algorithms In this paper, we compare nine representative influence maximization algorithms,that is,the Greedy algorithm(Greedy)[10],the single degree discount algorithm (SD) [13], the DPSO algorithm[49],the CGA algorithm[23],the CMA-IM algorithm[28], the CIM algorithm [27], the CDH-SHRINK algorithm[24], the CFIN algorithm [44], and the CNCG algorithm [47].The first three algorithms are representative non-community based ones while the remaining six algorithms are community based ones. In order to show the effectiveness of the proposed strategies in OCPSO,we also compare OCPSO with three variant versions of the proposed OCPSO, that is, OCPSO-NI, OCPSO-NM,and OCPSO-NLS.Specifically, OCPSO-NI is a variant of OCPSO by replacing the proposed initialisation method with random initialisation.OCPSO-NM is a variant of OCPSO by removing the proposed mutation strategy.OCPSO-NLS is a variant of OCPSO by removing the proposed local search strategy. We run all experiments under the IC Model[7].The influence spread of the ultimate seed set of each algorithm is calculated by running Monte-Carlo simulation for 10,000 times and the average performance of independently 20 runs is obtained as the final result for each algorithm.For OCPSO, the number of generationsmaxgen,the size of particle swarmpopand the propagation probabilitypare set to 50, 50 and 0.01,respectively.For each baseline algorithm, we adopt the parameters suggested in their papers.All comparison algorithms are implemented inPython3.6 and run on a PC with the CPU of Intel(R) Core(TM) i5-7500 @3.40 GHz and the memory of 16.0 GB. 4.2.1 | Validation of the motivation for OCPSO It is worth noting that community-based algorithms have shown their competitiveness in obtaining the influential seed nodes,however, most of them utilise non-overlapping community structures while ignoring the importance of influential overlapping nodes in the network.In this paper,we aim to separate overlapping nodes and non-overlapping nodes and measure their importance with different criteria to avoid ignoring the influential overlapping nodes.Thus,in this section,we want to validate the motivation of the proposed OCPSO by fully utilising the information of overlapping nodes and nonoverlapping nodes, in comparison with two variants of OCPSO.One variant is to treat overlapping nodes as nonoverlapping nodes.For fair comparison, the first variant of OCPSO is the same as OCPSO except that each overlapping node found by SLPA is viewed as a non-overlapping node,which is assigned to its most connected communities.For example,the overlapping node 8 in the network shown in Figure 1b will be assigned to Community 1,since node 8 has the largest number of connections with Community 1.And the other variant of OCPSO is the same as OCPSO except that the whole social network is treated as a community.In other words,the second variant of OCPSO does not perform community detection.Figure 5 presents the comparison results of OCPSO and its two variants on nine real-world social networks with seed sizekranging from 5 to 30,where the x-axis represents the number of seed nodes and the y-axis represents the influence spread of the seed set.The red line with circles(‘Overlapping’)represents the proposed OCPSO algorithm in this paper, the blue line with asterisks (‘Non-Overlapping’) represents the first variant of OCPSO and the black line with diamonds (‘No Community Detection’)represents the second variant of OCPSO.From this figure,it can be found that the influence spread of OCPSO is all superior to that of the two variants of OCPSO on the nine social networks with different values ofk.On the one hand, the comparison results of ‘Community Detection’ (including‘Overlapping’ and ‘Non-Overlapping’) and ‘No Community Detection’have verified community structure is indeed helpful to find influential nodes.On the other hand, the comparison results of‘Overlapping’and‘Non-Overlapping’have shown that by distinguishing overlapping nodes with the non-overlapping ones, the performance of the community-based algorithms can be further improved, which verifies the motivation of our method.Note that the performance gap shown in Figure 5h(dblp) and Figure 5i (youtube) is smaller than the other subfigures is due to the fact that average degree of these two networks(i.e.6.62 and 5.27 respectively)is smaller than the other networks.Note that all experiments are implemented under the IC Model, and the propagation probabilitypis set to 0.01 as recommended.Thus,the smaller the average degree of the given network,the smaller the number of nodes activated by the seed nodes,which leads to the smaller performance gap between the proposed algorithm with overlapping communities and that with non-overlapping communities. F I G U R E 5 Comparison results of overlapping community-based particle swarm optimization(Overlapping)and its two variants(Non-Overlapping and No Community Detection)on nine real-world social networks with k ranging from 5 to 30 at the step of 5.(a)Hamsterster friendship;(b)ego-Facebook;(c)HepPh;(d) epinions; (e) Email-Enron; (f) Brightkite; (g) Gowalla; (h) dblp; (i) youtube. 4.2.2 | The comparison results between OCPSO and baselines F I G U R E 6 The influence spread of 10 comparison algorithms on nine real-world social networks with seed size k ranging from 5 to 30 at the step of 5.Note that the Greedy algorithm cannot get a result within 24 h in one run on the last three large-scale social networks, thus their influence spreads are not provided on networks Gowalla, dblp, and youtube.(a) Hamsterster friendship; (b) ego-Facebook; (c) HepPh; (d) epinions; (e) Email-Enron; (f) Brightkite;(g) Gowalla; (h) dblp; (i) youtube. Figure 6 presents the influence spread of 10 comparison algorithms on nine real-world social networks with seed sizekranging from 5 to 30 at the step of 5.From this figure,it can be found that the Greedy algorithm can get the best influence spread on most of cases.The best performance of this Greedy algorithm is attributed to the fact that it mainly uses multiple Monte-Carlo simulations to estimate the influence spread of each node in the remaining nodes and selects one node with the largest marginal gain at each step untilknodes are selected.Although the algorithm can guarantee that the optimal solution be approximated to within a factor of (1 - 1/e-ϵ), its time complexity is very high due to the huge number of Monte-Carlo simulations.Thus,the computational time of the Greedy algorithm is the worst among comparison algorithms(see Figure 7).Note that the Greedy algorithm cannot get a result within 24 h in one run on the last three large-scale social networks,thus their influence spreads and running times are not provided on largescale networks Gowalla, dblp, and youtube in Figures 6 and 7 respectively. By further observing Figure 6,except the greedy algorithm,we can find that the proposed OCPSO can obtain the best performance on influence spread.Especially,compared with all other community-based algorithms(i.e.CGA,CMA-IM,CIM,CDH-SHRINK, CFIN, CNCG), the proposed OCPSO obtains the best performance on all networks.The better performance for OCPSO is attributed to the fact that OCPSO can make full use of overlapping nodes, non-overlapping nodes and their interactive information to obtain better performance. In addition, Figure 7 shows the running time of the 10 comparison algorithms on nine real-world social networks.As can be seen from this figure,we can find that the single degree discount algorithm SD can get the best computational time for all networks.The best computational time of SD is due to the fact it only ranks nodes according to degree.Due to this fact,its influence spread is the worst(see Figure 6).The reason for OCPSO achieving better efficiency comparing to the Greedy algorithm is mainly attributed to the fact that the approximate evaluation function(EDV)is used to evaluate influence spread and the framework of community-based algorithms can narrow the search space from the whole network to each community.In addition, the running time of OCPSO is comparable to the remaining algorithms(DPSO,CIM,CNCG,CDH-SHRINK, CMA-IM, CFIN, and CGA). From the experimental results above, we can make a conclusion that the proposed OCPSO can achieve a better balance between the influence spread and computational efficiency. 4.2.3 | Impact of the spreading models on results In the Figure 6,we have compared the proposed OCPSO with the state-of-the-arts on nine real-world social networks with the popular spreading model IC[7].However,it is well known that there are some other popular spreading models such as LT[8]and HD[50].Thus,it is interesting to investigate how these influence maximization algorithms perform on these different spreading models.To this end, we choose the three different spreading models (IC, LT and HD) for comparison.The influence spread of 10 comparison algorithms on nine real-world social networks with seed sizekranging from 5 to 30 on IC model, LT model, and HD model are shown in Tables 3–5 respectively. From the experimental results shown in Table 3, we can see that the Greedy algorithm can get the best influence spread on most of cases due to the fact that it mainly uses multiple Monte-Carlo simulations to estimate the influence spread of each node in the remaining nodes.Although the algorithm can guarantee that the optimal solution can be approximated to within a factor of (1 - 1/e).However, its time complexity is very high due to the huge number of Monte-Carlo simulations.Thus, the computational time of the Greedy algorithm is the worst among comparison algorithms.For example,the Greedy algorithm cannot get a result within 24 h in one run on the last three large-scale social networks, thus their influence spreads are not provided on large-scale networks Gowalla, dblp, and youtube in Tables 3–5 respectively. F I G U R E 7 The running time of 10 comparison algorithms on nine real-world social networks.Note that the running time of the Greedy algorithm on networks Gowalla, dblp, and youtube is not provided since the Greedy algorithm cannot get a result within 24 h in one run. T A B L E 3 The influence spread of 10 comparison algorithms on nine real-world social networks with seed size k ranging from 5 to 30 on IC Model[7],where the data in each parentheses is its ranking TA B L E 3 (Continued) T A B L E 4 The influence spread of 10 comparison algorithms on nine real-world social networks with seed size k ranging from 5 to 30 on LT Model[8],where the data in each parentheses is its ranking TA B L E 4 (Continued) By further observing Table 3,except the greedy algorithm,it can be found that the proposed OCPSO can obtain the best performance on influence spread.Especially,compared with all other community-based algorithms(i.e.CGA,CMA-IM,CIM,CDH-SHRINK,CFIN,CNCG),the proposed OCPSO obtains the best performance on all networks.The better performance for OCPSO is attributed to the fact that OCPSO can make full use of overlapping nodes, non-overlapping nodes and their interactive information to obtain better performance.From the experiments shown in Tables 4 and 5, we can find that the proposed algorithm OCPSO on LT model and HD model can also get the best tradeoff performance between effectiveness and efficiency,which consists with the comparison results thaton IC model shown in Table 3.The above comparisons have also further demonstrated the effectiveness of the proposed algorithm no matter what kind of spreading model is selected. T A B L E 5 The influence spread of 10 comparison algorithms on nine real-world social networks with seed size k ranging from 5 to 30 on HD Model[50],where the data in each parentheses is its ranking TA B L E 5 (Continued) 4.2.4 | Effectiveness of the proposed strategies in OCPSO To illustrate the effectiveness of the proposed initialisation,mutation and local search strategies in OCPSO, Figure 8 presents the influence spread(EDV)and convergence of the best solution obtained by OCPSO and its three variants (OCPSONI, OCPSO-NM, and OCPSO-NLS) with different generations(from 1 to 100)on nine real-world social networks.From this figure, it can be observed that OCPSO with the three proposed strategies can get the best performance among comparison variants on all networks in terms of both influence spread and convergence.Specifically, by comparing OCPSO with OCPSO-NI, it can be found OCPSO with the proposed initialisation strategy can converge much faster and get better influence spread than OCPSO-NI.For example, OCPSO can converge within 30 generations on most of networks while the convergence of OCPSO-NI needs more than 30 generations.In addition, the influence spread of OCPSO is obviously higher than that of OCPSO-NI on all networks.The similar results can also be observed by comparing OCPSO with OCPSO-NM, that is, OCPSO with the proposed mutation strategy can converge much faster and get better influence spread than OCPSO-NM on most of networks.The better performance is attributed to the fact that the mutation strategy is good for adaptively adjusting the ratio of the overlapping nodes and the non-overlapping nodes in the evolution to produce high quality seed set.Similarly,by comparing OCPSO with OCPSO-NLS, the effectiveness of the local search strategy is also demonstrated,that is,OCPSO can converge within 30 generations while OCPSO-NLS needs more than 60 generations, and the influence spread of OCPSO is much better than that of OCPSO-NLS on all networks.In summary, the above experimental results demonstrate that the proposed strategies including initialisation, mutation, and local search in OCPSO can not only speed up the convergence of OCPSO,but also improve the influence spread of OCPSO. In this paper, we proposed an overlapping community-based particle swarm optimization algorithm named OCPSO for influence maximization in social networks.Different from the previous community-based algorithms, we aim to separate overlapping nodes and non-overlapping nodes, and measure their importance with different criteria to avoid ignoring the influential overlapping nodes.To be specific, we first adopted an overlapping community detection algorithm to obtain the information of overlapping community structures.Then, we obtained the overlapping candidate nodes and non-overlapping candidate nodes by selecting a part of important communities.Finally,to make full use of overlapping nodes,non-overlapping nodes and their interactive information, we designed three novel evolutionary strategies such as initialisation, mutation and local search,which were used in OCPSO to effectively and efficiently find the top-kinfluential set of nodes.The experimental results on nine real-world social networks demonstrated that the proposed OCPSO can get a good balance between the influence spread and computational efficiency in comparison with nine baseline algorithms and three variants of OCPSO. F I G U R E 8 The influence spread(EDV)of the best solution obtained by overlapping community-based particle swarm optimization(OCPSO),OCPSONI, OCPSO-NM, and OCPSO-NLS with different generations on nine real-world social networks.(a) Hamsterster friendship; (b) ego-Facebook; (c) HepPh;(d) epinions; (e) Email-Enron; (f) Brightkite; (g) Gowalla; (h) dblp; (i) youtube. The proposed OCPSO has shown the effectiveness of overlapping communities used for influence maximization, in the future,we would like to extend OCPSO to solve influence maximization with budget constraints [51], which is more complex in real applications.It is also an interesting work to apply OCPSO for influence maximization on dynamic social networks,since the relationships between users such as follow and unfollow contained in social networks are always changing[52].In addition, although the proposed OCPSO algorithm shows good efficiency on both ordinary and large-scale social networks(e.g.millions of nodes),the efficiency of OCPSO on very large-scale social networks (e.g.billions of nodes) is not ideal due to the fact that it needs to perform evolutionary operations iteratively.In order to further speed up the efficiency of OCPSO on very large-scale networks, it is very interesting to extend OCPSO by using the multi-GPU systems[53]. ACKNOWLEDGEMENTS This work was supported in part by the National Natural Science Foundation of China(61976001,62076001,61876184),the Key Projects of University Excellent Talents Support Plan of Anhui Provincial Department of Education (gxyqZD2021089), the University Synergy Innovation Program of Anhui Province(GXXT-2020-050), and the Natural Science Foundation of Anhui Province(2008085QF309). CONFLICT OF INTEREST The authors have no conflict of interest. DATA AVAILABILITY STATEMENT The data used in this paper were derived from the following resources available in the public domain: Hamsterster friendships: http://konect.uni-koblenz.de/networks/petster-friendships-hamster, ego-Facebook: http://snap.stanford.edu/data/ego-Facebook.html, Brightkite: http://networkrepository.com/soc-brightkite.php, Gowalla: http://snap.stanford.edu/data/loc-Gowalla.html and youtube:http://snap.stanford.edu/data/com-Youtube.html are online social networks.HepPh:http://snap.stanford.edu/data/ca-HepPh.html and dblp:http://snap.stanford.edu/data/com-DBLP.html are collaboration networks.epinions: http://networkrepository.com/socepinions.php is a trust network.Email-Enron: http://snap.stanford.edu/data/email-Enron.html. ORCID Lei Zhanghttps://orcid.org/0000-0002-6447-2053 Fan Chenghttps://orcid.org/0000-0003-0175-0818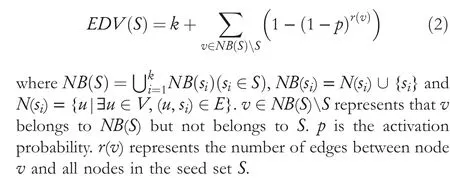
2.2 | Related work
3 | THE PROPOSED ALGORITHM OCPSO
3.1 | Overall framework
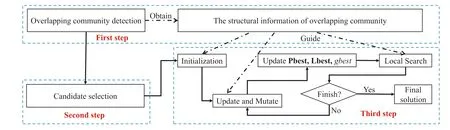


3.2 | Initialisation


3.3 | Update and mutate



3.4 | Local search


3.5 | Complexity analysis
4 | EXPERIMENTAL STUDY
4.1 | Experimental setup
4.2 | Experimental results and analysis



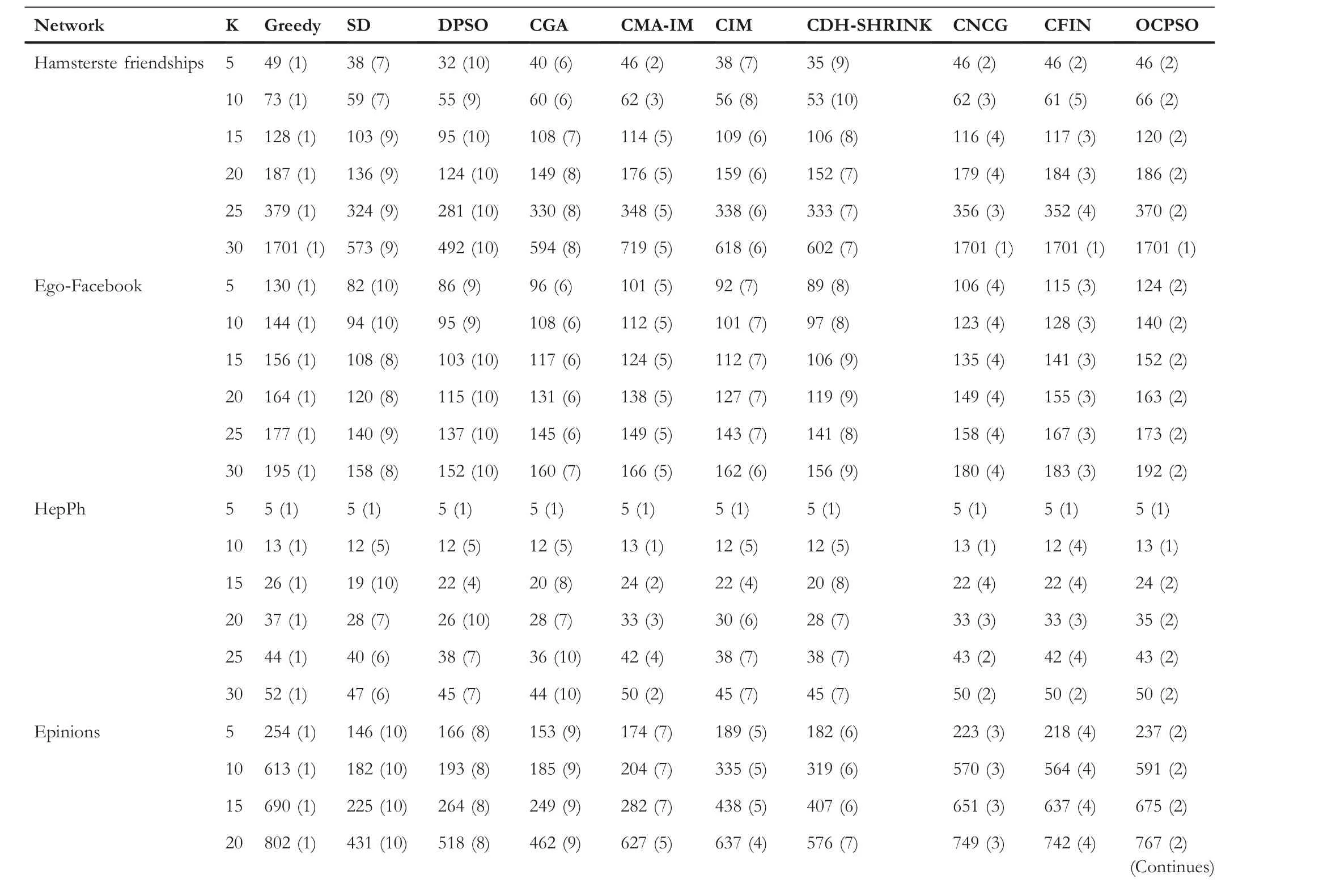
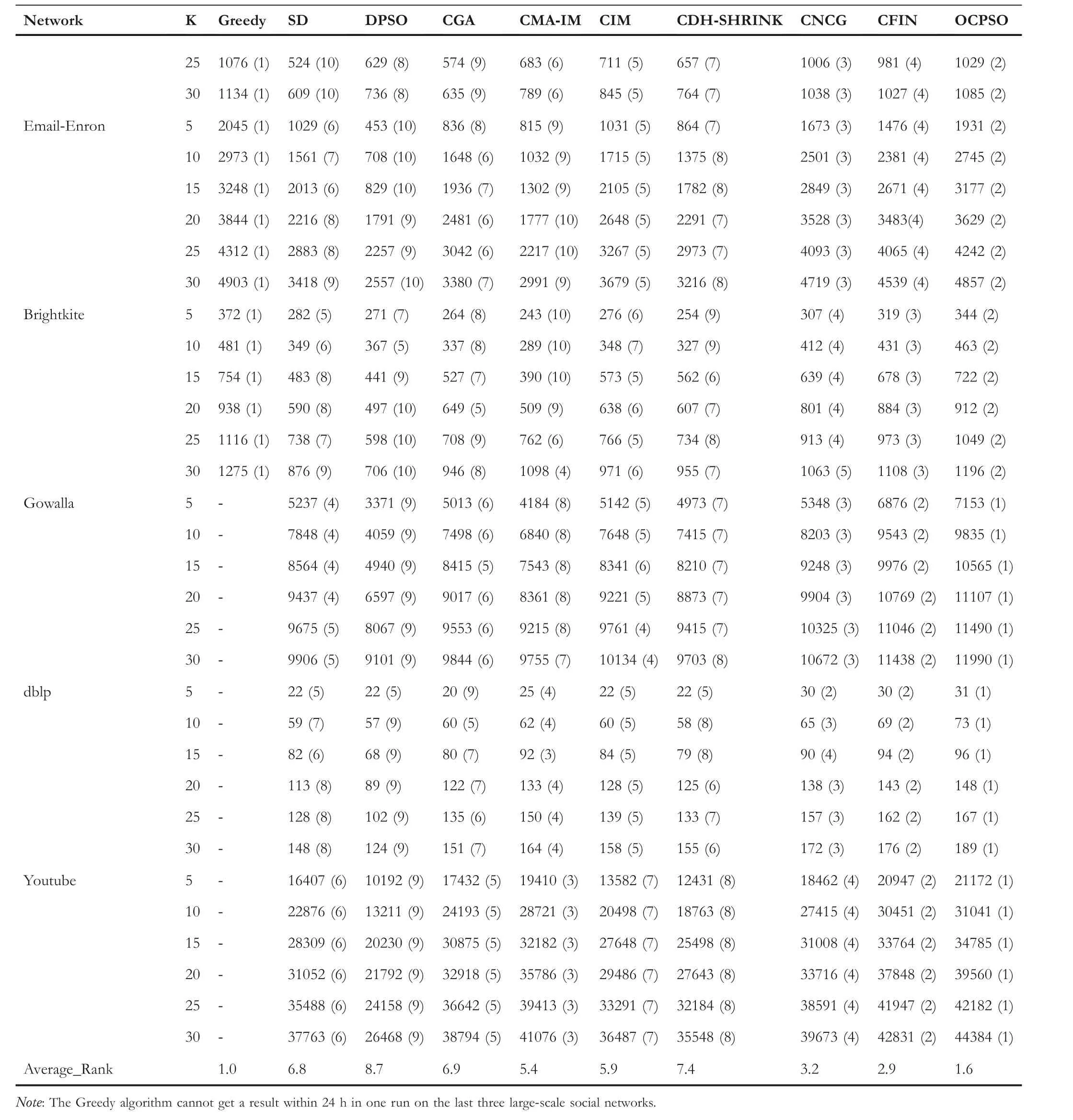

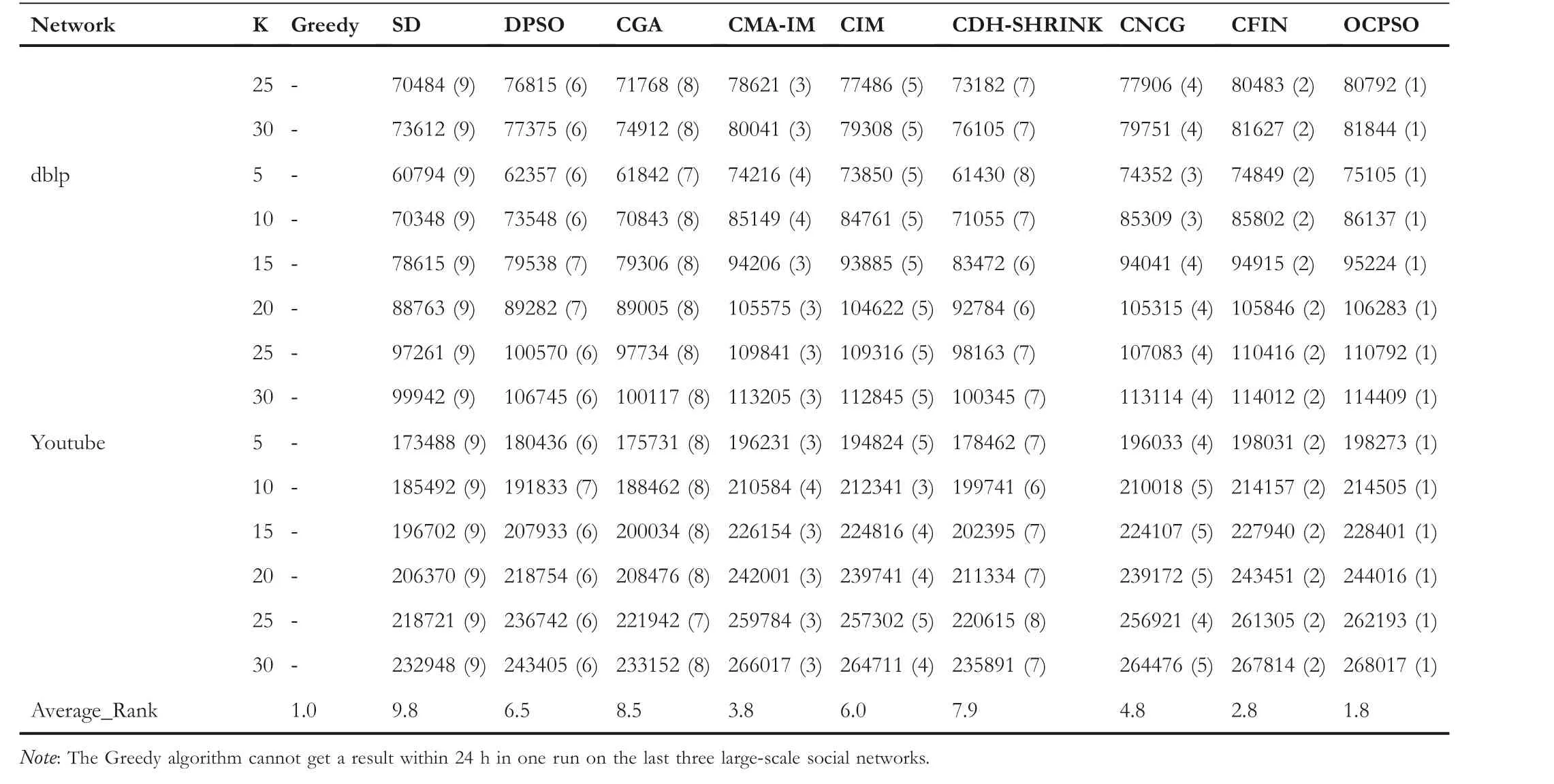
5 | CONCLUSIONS AND FUTURE WORKS
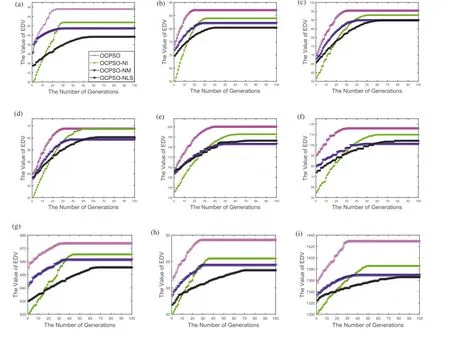
杂志排行
CAAI Transactions on Intelligence Technology的其它文章
- Fault diagnosis of rolling bearings with noise signal based on modified kernel principal component analysis and DC-ResNet
- Short‐time wind speed prediction based on Legendre multi‐wavelet neural network
- Iteration dependent interval based open‐closed‐loop iterative learning control for time varying systems with vector relative degree
- Thermoelectric energy harvesting for internet of things devices using machine learning: A review
- An embedded vertical‐federated feature selection algorithm based on particle swarm optimisation
- An activated variable parameter gradient-based neural network for time-variant constrained quadratic programming and its applications
