Fuzzy coloured petri nets‐based method to analyse and verify the functionality of software

Mina Chavoshi | Seyed Morteza Babamir

Department of Software Engineering, University of Kashan,Kashan,Iran

Abstract Some types of software systems,like event-based and non-deterministic ones,are usually specified as rules so that we can analyse the system behaviour by drawing inferences from firing the rules.However, when the fuzzy rules are used for the specification of nondeterministic behaviour and they contain a large number of variables, they constitute a complex form that is difficult to understand and infer.A solution is to visualise the system specification with the capability of automatic rule inference.In this study, by representing a high-level system specification, the authors visualise rule representation and firing using fuzzy coloured Petri-nets.Already, several fuzzy Petri-nets-based methods have been presented, but they either do not support a large number of rules and variables or do not consider significant cases like (a) the weight of the premise's propositions in the occurrence of the rule conclusion, (b) the weight of conclusion's proposition, (c) threshold values for premise and conclusion's propositions of the rule,and (d) the certainty factor (CF) for the rule or the conclusion's proposition.By considering cases (a)–(d), a wider variety of fuzzy rules are supported.The authors applied their model to the analysis of attacks against a part of a real secure water treatment system.In another real experiment, the authors applied the model to the two scenarios from their previous work and analysed the results.

K E Y W O R D S fuzzy logic, software engineering, verification

1 | INTRODUCTION

The non-deterministic behaviour of event-based systems with a high number of features,like water supply and transportation and traffic control systems, is defined based onfuzzy rules

where the rules are extracted from a high-level specification of the system and visualised.A method for the high-level specification is themode transition table, [1] which facilitates mapping the specification into the visual rules,and we use this in our proposed model (see Section 3.4).

A rule is expressed as anifstatement, where itsconditionandthenparts are called premise and conclusion, respectively.A rule may have a certainty factor (CF) where its premise and conclusion are stated as logical propositions with possible truth degrees.The following shows a sample rule with CF = 0.8,

where the premise contains two propositions with truth degrees of 0.6 and 0.7, and the conclusion does a proposition with a truth degree of 0.8.In addition to the truth degree,each proposition may have a weight indicating the impact of the proposition on the conclusion.In the following rule,values 0.4 and 0.6 show the impact (weight) of the premise propositions on the conclusion.

if high-temperature environment is(0.6)and high humidity environment is(0.7)then the electronic units are disabled(0.8).(CF=0.9)where whightemperatureenvironment=0.4and whighhumidityenvironment= 0.6.

Rules with a high number of variables make the system specification difficult to understand and infer.We aim to provide a solution that both visualises the representation of the rules and shows the rule inference,which is done by firing the rules.Such a solution can both (a) facilitate the understanding of the system behaviour and (b) automatise by inferencing the rules.By combining concepts of fuzzy set and coloured Petri-net theories with fuzzy coloured Petri-nets, the nets have shown their effectiveness in satisfying cases (a) and(b)for uncertain information and its fuzzy inference.Petri-net can be used to visually model the behaviour of a system and can be executed at the model level so that conclusions and inferences can be made.A Petri net consists ofplaces(nodes),arcs,and transitions, where each transition has input and output places.A transition isenabledwhen its input place(s)has/havetoken(s).Considering the capability of fuzzy logic in managing the ambiguity and uncertainty of the environment,they may be combined with Petri-nets to create fuzzy Petrinets, which is an efficient tool for describing fuzzy systems.A coloured and fuzzy Petri-net is a Petri-net with coloured and fuzzy tokens,where a coloured token denotes a type.The formal definition of coloured fuzzy Petri-nets is presented in Section 3.

Based on fuzzy Petri-nets, the authors in Refs.[2, 3]visually represent rules with high-level variables and their application in the reasoning process.In the model presented by the authors in Ref,[3],the weight of premises and conclusions,the threshold value, and CF for rules are considered.Twodimensional uncertain linguistic variables (2DULVs) are used for CF and threshold values.Moreover, the interaction between the propositions is included in the reasoning process.

In the model presented in Ref.[2], the truth degree of propositions, the threshold value, and CF value are included for the rules, wherePythagoreanfuzzy variables (PFVs) are used to represent the values and applied to the reasoning process.However, models in Refs.[2, 3] will be very complicated and unimplementable for systems with a large number of rules and variables.

In our previous work [4], using a hierarchical manner, we presented a model for visualising and the inference reasoning a high number of rules, where a large number of features are handled using coloured Petr-nets;however,the model does not support the cases that have been considered in the previous studies.

Inspired by Refs.[2,4]and[3],a hierarchical(nested)fuzzy coloured Petri-net is proposed from a high-level specification expressed by themode transition table[1].The net has the capability of analysing systems whose behaviour is expressed in non-deterministic environments with a large number of rules and variables.To deal with the uncertainty, 2DULV and PFV are used so that the reasoning process can be done more intelligently.Figure 1 shows the workflow of our solution in general.Contributions of our proposed model in this paper are as follows:

• Presenting a method to map a high-level specification to a rule-based visual model

• Reducing complexity of rule representation through the visualised model and automatising the inference reasoning,

• Supporting the high number of the rules where overlapping propositions between premise of different rules may exist;this is done through the hierarchical property of the visualised model,

• Supporting rules with the high number of variables through the coloured tokens in the coloured Petri-nets,

• Supporting non-deterministic knowledge in the rules using fuzzy coloured Petri-nets.

The paper continues as follows;in Section 2, related work is reviewed.In Section 3, concepts,FCPN, 2DULV, PFV, andMode Transition Table, are introduced.In Section 4, our proposed approach is presented and,in Section 5,it is applied to two real case studies,and the results are analysed.Finally,in Section 6,conclusions are drawn,and future work is proposed.

2 | RELATED WORK

In the literature review related to FPNs [5], the authors selected 272 articles from 2000 to 2022 with the aim of creating a global picture of developments, focussed areas, and research trends.In this study, the topics of (a) ‘genetic algorithm’,‘risk assessment’,and‘fault diagnosis’as hot studies and(b) ‘expert system’, ‘knowledge representation’, ‘fault diagnosis’, and ‘fuzzy reasoning’ as important research topics for future research directions were introduced.

In fuzzy Petri nets, reasoning is done using (1) the reachability tree-based method,which is derived from Petri-net and has the graphical capability, (2) the algebraic-based method(with the mathematical capability) where matrices are derived from Petri-net, and algebraic operations are done on the matrices, and (3) high-level fuzzy Petri-net-based method.

F I G U R E 1 The workflow of the proposed method.

2.1 | Reachability tree‐based methods

In Refs.[6, 7], fuzzy Petri-nets are derived from fuzzy production rules.In Ref.[7], a backward reasoning algorithm,which is an interactive algorithm, is used.This algorithm automatically generates the And-Or graph and takes the truth degree of the proposition in each leaf node from the user;then,it traverses from the leaf nodes towards the root and calculates the truth degree of the proposition in each other node.The values of the certainty factor of a rule and the truth degree of each proposition are expressed in non-fuzzy.This is why an improved weighted fuzzy Petri-net was presented in Ref.[8],where the fuzzy numbers were considered for the mentioned parameters.However,the fuzzy algorithm presented in Ref.[6]is not suitable for all types of data; therefore, in Ref.[6], the algorithm was modified as well as the hierarchical fuzzy Petrinets for data abstraction were used.

2.2 | Algebraic operation‐based methods

In Ref.[9],a kind of generalised fuzzy Petri-net was presented for representing fuzzy rules and reasoning for a Decision Support System, where three triangular operators were presented as substitutions of algebraic operators of maximum,minimum, and multiplication.

In Ref.[10], a two-stage decomposition algorithm was presented to overcome state space explosion in large-scale fuzzy Petri-nets with high complexity.This algorithm consists of a backward search and a forward strategy, where a large-scale fuzzy Petri-net is divided into sub-fuzzy Petri-nets by using an index function and an incidence matrix; then,the reasoning is done.Through the backward step, reasoning paths are automatically identified.

In Ref.[11], a dynamic adaptive fuzzy Petri-net and a parallel and algebraic reasoning algorithm are proposed,which can perform the reasoning process dynamically and automatically.It is called dynamic adaptive because it can change the fuzzy rules by changing the propositions during the reasoning process and give them a dynamic nature.

In Ref.[12], an approach was proposed to acquire knowledge and its representation, using an intuitive fuzzy reasoning approach and dynamic adaptive fuzzy Petri-nets.

In Ref.[13], a fault Diagnosis and Cause Analysis was presented using a fuzzy evidence reasoning approach and dynamic adaptive fuzzy Petri-nets.

In Ref.[14],an Intuitionistic Fuzzy Petri-net was presented using the Intuitionistic fuzzy set,and a matrix-based reasoning algorithm was proposed.

In Ref.[15],the authors suggested(a)a new type of Petrinet called spherical linguistic Petri-net using spherical language sets to facilitate knowledge representation and reasoning, (b)the acquisition of knowledge from a large group of experts to determine knowledge parameters, and (c) an inference algorithm to perform reasoning.Moreover, they show that the presented model is efficient against the uncertainty of experts'opinions and the complexity of rule-based systems.

In Ref.[16], a linguistic reasoning Petri-net as well as an ordered weighted linguistic reasoning algorithm were presented for knowledge representation and reasoning.The fuzzy production rules of rule-based expert systems are modelled using a linguistic reasoning Petri-net, and the reasoning process is done automatically.The weight of propositions of premise and conclusion are considered in the linguistic reasoning process.Moreover,the truth degree of propositions and the rule certainty factor are considered in linguistic 2-tuples.

In Ref.[3],by combining Pythagorean fuzzy sets and fuzzy Petri-nets,a new model of fuzzy Petri-nets called Pythagorean fuzzy Petri-nets was presented to express rules and reasoning;In addition, a clustering method based on the opinion of a large group of experts was presented to determine the truth degree of input places of the Petri-net.

In Ref.[2], a new type of fuzzy Petri-nets called twodimensional uncertain linguistic Petri-net (2DULPN) was presented, which is a combination of 2DULVs and Choquet integral.Moreover, some new aggregated operators based on the Choquet integral were used in the reasoning process by considering the interactions between propositions.

2.3 | High‐level fuzzy petri‐net‐based methods

In Ref.[17],a generalised fuzzy Petri-net called adaptive fuzzy Petri-net and a modified back-propagation learning algorithm based on the net were presented.The proposed method has the ability to learn like a neural network.

In Ref.[18], a high-level fuzzy Petri-net for modelling fuzzy rules in the form ofif-thenandif-then-elsewas presented based on which an efficient algorithm for automatic reasoning of fuzzy information was presented.

In Ref.[19], to increase the knowledge representation capability, the weight of propositions of premise and the conclusion is considered,and a generalised fuzzy Petri-net and a multi-level fuzzy reasoning method were presented.

In Ref.[20],an intuitionistic fuzzy Petri-net was presented using the combination of intuitionistic fuzzy sets with Petrinets;then,a reasoning process in which a weight is considered for input places of transitions.

In Ref.[21], a concurrent and forward reasoning method was presented for rule-based systems using coloured fuzzy Petri-nets.

In Ref.[22],an intuitionistic fuzzy Petri-net was presented using the combination of intuitionistic fuzzy sets and Petrinets;then,a reasoning process based on matrix operations was presented to take advantage of parallel computing.

In Ref.[4], we represented the behaviour of a pacemaker using hierarchical fuzzy coloured Petri-net (HFCPN), which(1)covers the overlapping regions generated by the input fuzzy numbers and(2)improves the time of finding suitable rules up to 92%.Furthermore,an intelligent software agent checks the runtime behaviour of the pacemaker software in vital and unexpected situations and directs the software decision if an unacceptable value is found.

2.4 | Analysis of methods

In the following, the issues may occur while using the mentioned models that are introduced.

• All of the models are flat [4], which are hierarchical.In the flat ones,the number of transitions depends on the number of rules.Therefore, by increasing the number of rules, the number of transitions is increased,leading to the complexity of the model

• In the flat models,a variable and its values as a proposition are mapped to a place of the Petri-net.Therefore,in case of a high number of variables and the variables with a high number of values,such models face a complex model with a high number of places.Such an issue makes the management of the model difficult.In the case of overlapping premise's propositions, in our proposed model, tuplecoloured tokens and applying a hierarchy of transitions to the propositions prevent the repetition of places.But,in the flat models,it causes an increase in the arcs and places of the Petri-net, leading to a complex model for managing.

• Considering the reasoning process,flat models consider just one type of the process and its knowledge parameters; but,our proposed model considers a flexible and wider reasoning process by which the capability of algebraic reasoning methods is provided.Moreover, based on the employed reasoning process, it is feasible to consider each type of parameter related to knowledge of rules and express by high-level variables.

• While our proposed model is event-based,other ones are not

• The model presented [4] is hierarchical (not flat), but types of different knowledge parameters were not considered and expressing the parameters in terms of high-level variables was not done.Moreover,it does not have the flexibility that we provide by applying algebraic reasoning methods.

3 | PRELIMINARIES

3.1 | Fuzzy coloured petri‐net

In Section 1,we informally explained fuzzy coloured Petri-nets(FCPNs);now,we present its formal definition.The flat(nonhierarchical)FCPN is defined as tupleFCPN=(P,T,C,D,I,O,α,β) [4] where

P= {P1,P2, …,Pk} is a finite set of places.

T= {T1,T2, …,TL} is a finite set of transitions.

P∪T= ∅

C= {C1,C2, …,Ci}

D= {DP1,DP2, …,DPk}

I:P→Tmaps a place to a transition.

O:T→Pmaps a transition to a palce.

α:Cij→[0…1]

β:T→[0…1]

C is a finite set of linguistic variables,where each variable is shown asCj=Cj1,Cj2, …,Cjkandkis the number of fuzzy expressions of the variableCj.For instance, the linguistic variable of thelevel transmitteris described by five fuzzy expressions of ‘very low’, ‘low’, ‘medium’, ‘high’, and ‘very high’.DPi∈Dspecifies the finite set of coloured tokens at placePi.Each token is represented as an n-tuple containingnpairs(Cij,αij),whereCij∈Cjandαijis the truth degree ofCij.Parameterβshows the CF of the rule, which denotes the probability of firing the related transition in the Petri-net.

3.2 | Two‐dimensional uncertain linguistic variable

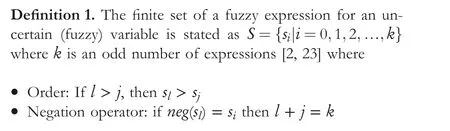
Definition 2.An uncertain variable has an uncertain value changing in [0,1], which is divided into a number of subintervals.The lower and upper limits of [0,1] and the subintervals are indicated by two linguistic expressions.Therefore an interval/sub-interval is defined as～s= [˙sa,˙sb] where ˙saand ˙sbbelong to the set S [2, 24].

3.3 | Pythagorean fuzzy variable (PFV)

Definition 8.Let X be a fixed and non-empty set.A Pythagorean fuzzy set P in X is defined as four ([3])

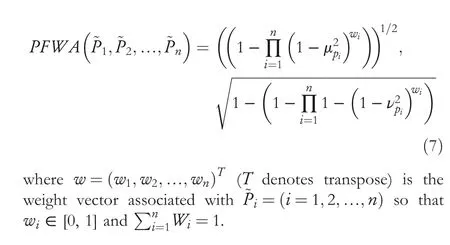
3.4 | Mode transition table

The mode transition table([1])is a description of the system's behaviour in the form of a table in which each row of the table represents the event and conditions that cause a change in the system's state.It is a formal and expressive tabular method for describing event-based systems.In this method, at first, the problem's variables are determined;then,(1)thestatevariables,which show the modes or states of the system and (2)eventsandconditionsare determined.A value of a state variable indicates the name of a system behaviour mode.The value of a condition/event variable is T (true) or F (false); in case of a condition,the value remains fixed during a mode change(from the current mode to a new one) and, in case of an event, it changes from T to F or vice versa during a mode change.

Table 1 shows a typical row in the mode transition table;for a system withnvariables,it will haven+2 columns,where the leftmost and rightmost ones are thecurrentmode and thenewmode.The next columns are considered for the variables playing the role of a condition/event,where‘t’or‘f’denotes the variable is considered as a condition and,‘@T’or‘@F’does the variable is done as an event.Notation‘t/f’denotes the variable value is true/false during the mode transition and‘@T’/‘@F’does the variable value changes from false/true to true/false during the mode transition(from a current one to a new one).Notation‘-’denotes do not care for a variable value in a mode transition.

4 | PROPOSED APPROACH

Our proposed model is used to specify and verify the behaviour of the systems that make a transition from a normal mode to an abnormal one.The mode transition is specified through the mode transition table, whose modes arenormalandabnormal, and the abnormal ones include different modes.When the system makes a transition,the new mode is verified with its truth degree.To calculate the degree, we used two methods based on PFV with 2DULV, inspired by Refs.[2, 3].Considering Figure 1, the proposed method is done through four steps.

T A B L E 1 Mode transition table.

• Through a gradual mapping in the first step, according to the problem nature,condition and event variables and mode variables with their values are extracted and mapped to the Mode Transition Table (see the blue bubble in Figure 1).However,this table does not provide(1)automatic inference and(2)considering the uncertainty in the reasoning process.Moreover,there may exist overlap propositions between the premise of different rules in which the representation of hierarchical rules is needed,and the table does not have such capability,

• Therefore, in the second step, based on the hierarchical fuzzy Petri-net,we map the table representation(Table 2)to the model, and the extracted rules from the table are included in the Petri-net;this step is specified in Figure 1 by yellow bubbles.In each row of the table, it is shown under what events and conditions,the system goes to an abnormal state.A table's row indicates a rule,whose premise contains the event and condition variables, and the conclusion does an abnormal mode.The number of the table's rows depends on the number of abnormal modes,

• In the third step, the weight of each proposition, its threshold, CF rules are taken from the expert and included in the rule(see the green bubble in Fig.I.)The truth degree and value of each variable in the propositions are obtained according to the membership function.For fuzzy numbers and the possible occurrence of abnormal modes, fuzzification is done separately according to the high-level variable used in the reasoning process,

• Finally, in the fourth step, the reasoning process based on the high-level variable is performed.The designed model has the ability to perform various mathematical reasoning methods based on various high-level variables.

In the following, we deal with the mapping (step 2) in Section 4.1 and the reasoning process (Steps 3 and 4) in Section 4.2; all steps except the reasoning process are done manually.

4.1 | Mapping mode transition table to the proposed petri‐net

Given that the system hasnvariables (see Table 2), the mode transition table will containncolumns.For each row of the table, we consider the variable (condition and event) values leading to the mode transition;then,the corresponding rule isobtained.Table 3 shows the mapping of the mode transition table of elements of the proposed Petri-net.

T A B L E 2 Mode transition table of the proposed model.

Given that we havenvariables andmabnormal states,we will have an input place,m+1 output places, and 2(n-1)+1+6=2n+5 middle places in the proposed Petri-net.Figures 2–4 show levels zero, one andnof the Petri-net,respectively.

At the zero level (Figure 2), place ‘system states’ contains coloured tokens and shows the system status at any time.Acoloured token contains the value and truth degree for all (n)system variables at a time where the value is shown in“.”,and the truth degree is shown in [.].

T A B L E 3 Mapping mode transition table to the proposed fuzzy coloured hierarchical petri-net.

By firing transition E,the coloured token related to timetindicating the previous state,is removed from the input place,and a token related to timet+1 indicating the new state(Current one) is inserted in the output place.The value and truth degree of variables are shown as expressions Cvar1,Cvar2, Cvar3 , …, Cvarn at timestandt+1.Next, by firing transition D,place“Last State”will contain the coloured token related to the previous state of the system.

By firing transition C, a token from place “Current State”(indicated by expressions Cvar1,Cvar2,Cvar,…,Cvarn) and a token from place“Last State”indicated by expressions(Lvar1,Lvar2,Lvar3,…,Lvarn) are removed, and place “Ready to compare”includes token(Lvar1,Cvar1),(Lvar2,Cvar2),(Lvar3,Cvar3),…, (Lvarn,Cvarn).

In each level,a high-level transition indicating a variable is decomposed as a Petri-net; accordingly, in addition to level zero,we will havenPetri-net fornvariables,where the variable value is checked for the condition or event.If a variable can takexvalues, its corresponding level, if it is not the last level,contains 2*xlow level and one high-level transitions(related to the next variable)(Figure 3).For the level corresponding to the last variable (indeed, the last level), just 2*xlow-level transitions will exist (Figure 4).

From 2*xtransitions in a level,xones are for the previous values of the variable and otherxones for the current values of the variable.At the zero level, according to the reasoning method and type of the variable, the zero truth degree (indicating the zero probability of a proposition occurrence) is considered for a proposition and replaces the term TD0.

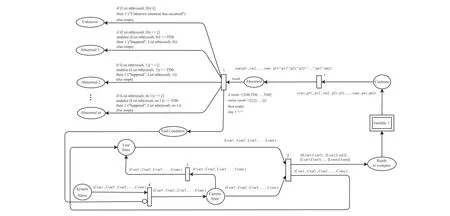
F I G U R E 2 Level zero of the proposed petri-net.

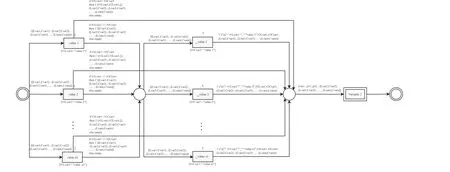
F I G U R E 3 Level 1 of the proposed petri-net.

F I G U R E 4 Level n of the proposed petri-net.

Levels 1 andncheck the status of the first and last variables,respectively;this is done for all levels.Now,we explain a level,say level 1(Figure 2).The coloured token in place“Ready to Compare”moves to level 1 through the expression((Lvar1,Cvar1), (Lvar2,Cvar2), (Lvar3,Cvar3),…, (Lvarn,Cvarn)).Each of these variables in the expression contains a value(indicated by#1)and a truth degree(indicated by#2).Notation#1Lvar1 in the conditions of low-level transitions denotes the value of the variable in the previous state.If the value of the variable is equal to one of the values defined for the desired variable,the corresponding low-level transition is enabled and fired.After firing, two situations occur, which are checked through the conditions on the arcs.

First case: Given that the variable has a fixed value (i.e.,#1Lvar1 = #1Cvar1), thethenpart of the followingifis executed(i.e.,#1Lvar1,#2Lvar1,[]replaces(Lvar1,Cvar1)as a result, and it is transferred to the next level.

In this case, the previous value of the variable is specified and,in order to check the next value of the variable,the token moves to level 1 in the output place of the lower level transitions.

The expression #1Cvar1 in the conditions of low-level transitions refers to the value of the variable in the current state.If the current value of the variable is equal to one of the values defined for the variable, the corresponding low-level transition is enabled and fired.After firing one of the lowlevel transitions, the type of the variable event is specified.Therefore, the following expression, as a result of this, check replaces the expression(Lvar1,Cvar1)and is transferred to the next level.

Expression #1Lvar1 contains the previous value of the variable, and the “value” denotes the current value of the variable, which is determined according to the fired low-level transition.Expressions #2Lvar1 and #2Cvar1 refer to the truth degree of the variable value in the previous and current states, respectively.

Finally, token (var1,p11,p12, (Lvar2,Cvar2), (Lvar3,Cvar3),…, (Lvarn,Cvarn)) is transferred to the next level in order to check the second variable.The expression“var1”contains the check result of the first variable, and “p11” and “p12” show the truth degree of the variable value; if the variable value is fixed (i.e., it denotes a condition), “p12” is null (denoted by“[]”), but, if the variable is not fixed (i.e., it denotes an event where the variable has two values),then it has two truth values.By firing transition “B” in level zero, theresfunction is called to perform the reasoning process by receivingn+1 input parameters.The parameters are formed based on the token placed in the place“Coulmns”,that is,(var1,p11,p12,var2,p21,p22,…,varn,pn1,pn2).

The signature of the functionresisres(var1,var2,…,varn,p11^^p12^^p21^^p22^^…^^pn1^^pn2) where var1 to varn denotes the state ofnvariables, and p11^^ p21 to pn1^^pn2 form an array,containing the truth degrees of the variables.In CPNTools,notation“^^”is used to concatenate two elements.

In transition B, by calling theresfunction, the rule related to the current state of the system and the parameters proposed by the expert are extracted, in order to perform the reasoning process by the abstract and flat Petri-Net (Figure 5).In this figure, the number of output propositions from the transition will be fixed and equal to the number of abnormal modes,but the number of input propositions to the transition will be variable.If the value of a variable is fixed, only one place will be considered for that variable(indicated by a white place),but if the value of a variable changes,the next state for the variable will be considered(indicated by a grey place).In fact,for such variables, two places are considered.

4.2 | Reasoning process

The reasoning process may be done by two methods.

4.2.1 | Reasoning process based on PFV

Based on Ref.[3]and according to the system status and truth degrees ofnvariables, the reasoning process is carried out through four steps, and the truth degree is determined.

• Step 1: The weight of propositions in the premise and conclusion parts and the rule CF related to the current status of the system are extracted.The same threshold value is considered for all the propositions of the premise and is stored in a variableTh.

• Step 2: The transition’s enabledness (E, Equation (8)) is checked.This is done by checking the truth degree of input places to the transition.If the truth degree of all of the places is greater than or equal to their threshold, the transition is enabled.In Equation(8),the functionMK(Pj)returns the truth degree of placePj,Thshows the threshold value,andnis the number of the premise propositions.

• Step 3: If the transition is enabled, its truth degree is obtained asgammausing Equation (9), whereμandvwere introduced in Definition 8,piis placei, and ∏denotes multiplication.If the transition is not enabled,gamma= [0.0,1.0].

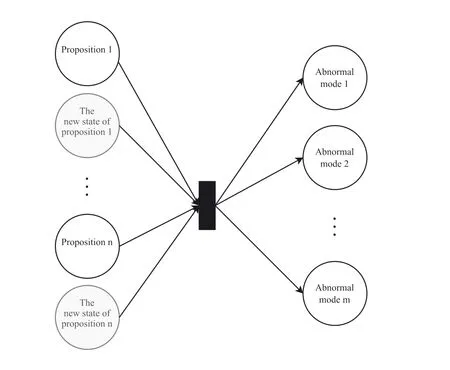
F I G U R E 5 Abstract flat Petri-net.

• Step 4: The truth degree of the output places is calculated and,according to the weight of the conclusion propositions,the vector of the truth degreeresultfor the conclusion is obtained using Relation 10, whereUis the rule certainty factor.

Based on the PFV,the general form of theresfunction for our model is shown in Figure 6.

4.2.2 | Reasoning process based on 2DULV

Based on Ref.[2] and considering the system status and the truth degree fornvariables, through functionres, the reasoning process is carried out in five steps and the truth degree is determined.

• Step 1: For the rule related to the current status of the system, the weight of the propositions of the premise and conclusion, the threshold value for the premise's propositions, and the rule CF are extracted.The threshold value is assumed to be the same for all the premise's propositions.

• Step 2: Based on the truth degree and weight of the premise's propositions, the truth degree of the transition is calculated asTr(11)

• Step 4: If the value of variable E is non-zero, the truth degree of the output places of the transition is calculated by calling functionpsiby Relation 13, whereUis CF.

F I G U R E 6 The general form of the res function based on PFV.

• Step 5: According to the weight of each conclusion's proposition,a vector of the truth degree of the propositions is constituted.

The general form of functionresfor our model based on 2DULV is shown in Figure 7.

After the reasoning process, a list of the calculated truth degrees forabnormalstates is held in placeabnormalas the output of functionres.However, if the resulting state isunknown,a list containingm(see Figure 2)null lists is held in the place.

By firing the transition, in case of anabnormalstate,the calculated truth degree of each abnormal state is held in the related place by the variableresultand by considering the conditions on the input arc of the place.In case of anunknownstate, a token with expression “Unknown status has occurred” is held in place Unknown.In case of abnormal or unknown, a token with content “+” is held in place “End Condition”, and consequently, the process stops and the result of the reasoning is reported to the user.The following condition shows place “End Condition” will not have any token (indicated by empty), and the process continues if the result value shows that it is not abnormal/unknown; otherwise, it will have token “+” and, the process will stop.

5 | EXPERIMENTAL RESULTS

5.1 | Assumptions

Given that the synergistic coefficient is zero; all the premise's propositions are considered to have the same weight in both of the reasoning methods.Out of the propositions of the conclusion part, the one that represents the current status of the system has been assigned weight 1, and others have been given weight zero.

F I G U R E 7 The general form of the res function based on 2DULV.

In the reasoning process, based on PFV, CF = (1.0,0.0) is considered for all rules,and threshold=(0.0,1.0)is done for all the premise's propositions.

Because it is difficult to estimate the truth degree of each proposition in the real world, we, first, calculate the truth degree of each variable by using the membership functiontrapezoidal.Considering the calculated degree, we specify the corresponding interval in Figure 8;then,for each membership interval, based on Ref.[35], an equivalent Pythagorean fuzzy value will be assumed (Table 4).

In the reasoning process that is based on 2DULV,we have assumed two setsSIIandSIas follows.Therefore,parametersgandtwill be six and four, respectively.

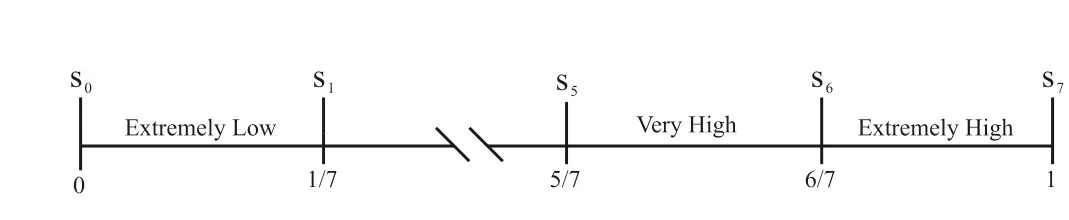
F I G U R E 8 Scaling the probability of the proposition truth based on values of the PFV.

T A B L E 4 PFV values of the memberships in Figure 8.

5.2 | Applying the proposed model for safe water treatment systems

5.2.1 | The safe water treatment system and its assumptions

In order to analyse and evaluate the proposed approach, the case study for the Safe Water Treatment System ([36]) is considered, which represents an industrial water treatment plant.It consists of six processes to purify and prepare five gallons of water per minute for distribution in the water distribution system.Due to the size of this system, we have used the proposed model only for the first process (Figure 9).This process of the system has five variables, P101, P102, LIT101,FIT101, and MV101, where three variables, P101, P102, and MV101, have definite values and two variables, LIT101 and FIT101, have fuzzy numbers.Table 6 shows the details of the variables, and Figures 10 and 11 show the membership function for FIT101 and LIT101, respectively.

5.2.2 | Attacks

The system has two pumps, 1 and 2, where pump 2 is considered as a backup; for the first process of water purification, four attacks may occur:

T A B L E 5 Scaling the probability of the proposition truth for the first and second dimensions based on the 2DULV.

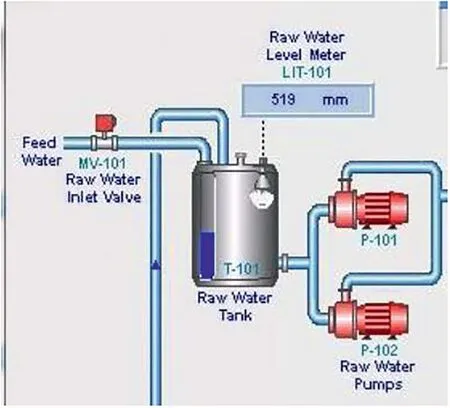
F I G U R E 9 The first process of the secure water treatment system.

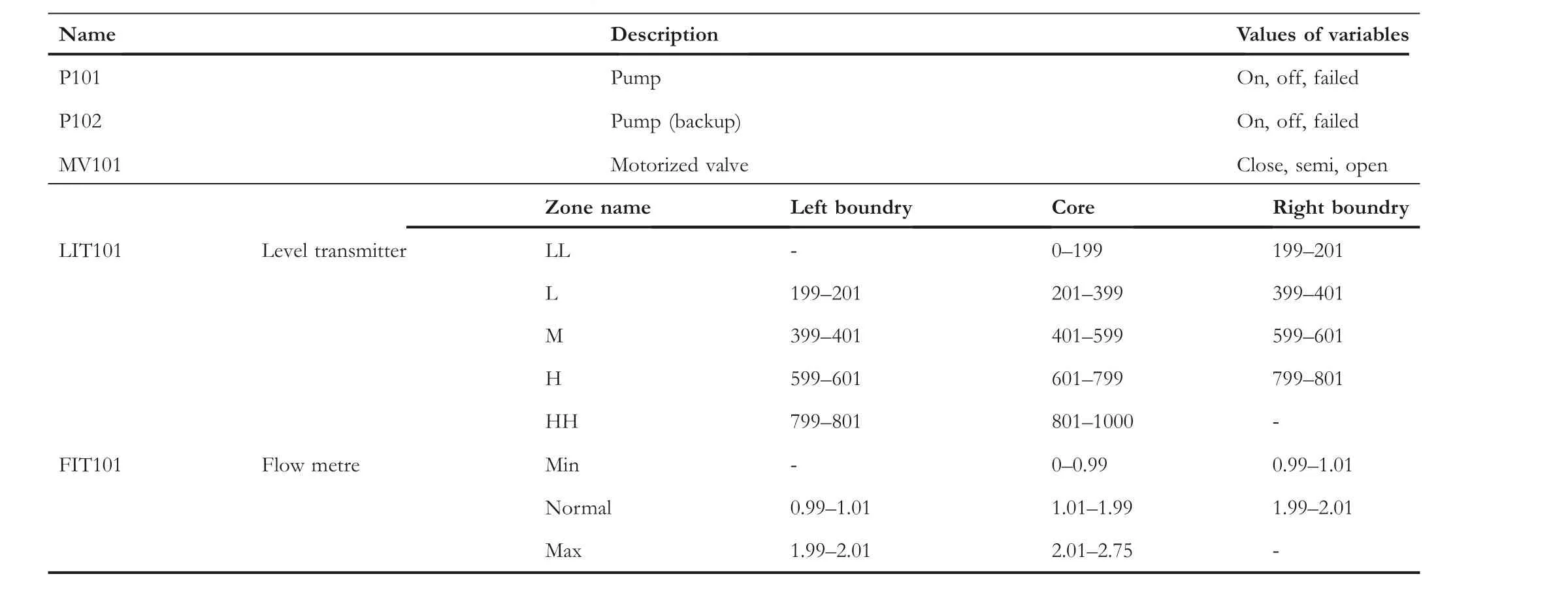
T A B L E 6 Variable values of the secure water treatment system.

F I G U R E 1 0 Membership function for the FIT101 variable.

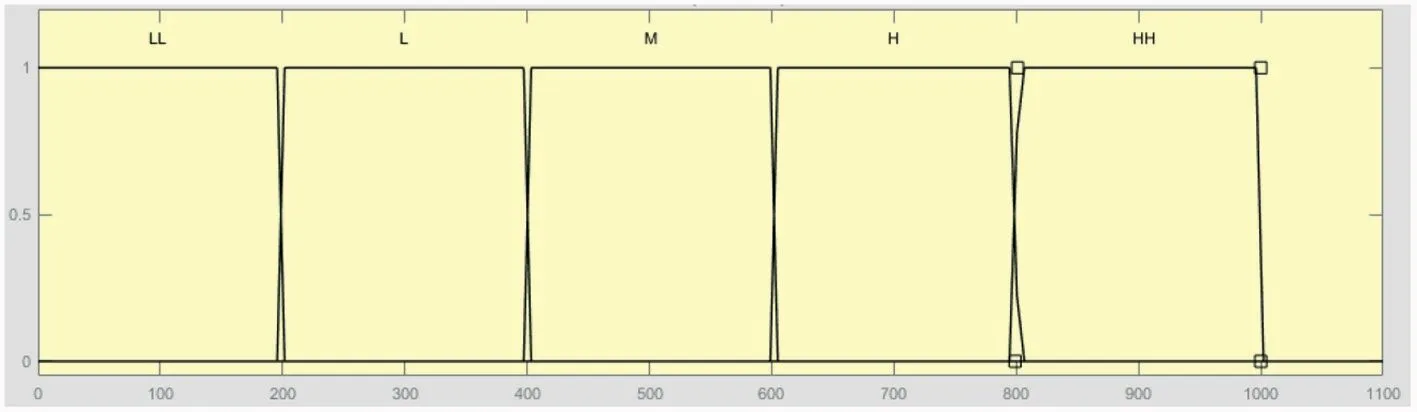
F I G U R E 1 1 Membership function for the LIT101 variable.

• Pipe burst:The attacker switches the second pump from off to on when pump 1 is on,

• Stops flow: The attacker switches pump 1 from on to off when pump 2 is off;or he/she switches pump 2 from on to off when pump 1 is damaged,

• Tank overflow: The attacker opens the motorised valve when the tank level transmitter is in range M, H, or HH,causing the tank to overflow,

• Tank underflow and damage pump: The attacker changes the level transmitter to range ‘high’ or ‘very high’ when the level shows low or medium;this deceives the system,leading to close the motorised valve and finishing the tanker's water;this causes the pump to work idle and get damaged.

Table 7 shows the Mode Transition Table for the attacks.First, it is checked for the normal state; then, occurring an attack is verified.There exist 83 normal states, which we reduced to 36 states and considered a rule for each state.If the status is neither normal nor one of the defined attacks, it is recognised as an unknown situation.

Considering Table 7, the rules are defined as follows:

1) if (p1 = “on” andalso p2 = “@off_on”) then Pipe bursts

2) if ((lit = “M” orelse lit = “HH” orelse lit = “H”) andalso mv = “@close_open”) then Tank overflow

3) if (fit = “normal” andalso (lit = “@M_HH” orelse lit = “@M_H” andalso mv = “open”) then Tank underflow/Damage pump

4) if ((lit = “@LL_HH” orelse lit = “@LL_H” orelse lit =“@L_HH” orelse lit = “@L_H”) andalso mv = “open”)then Tank underflow/Damage pump

5) if (p1 = “@on_off” andalso (p2 = “off” orelse p2 =“faild”)) orelse (p1 = “fiald” andalso p2 = “@on_off”)then Stops flow

Figure 12 shows a part of our Petri-net model for the system where 2DULV is used.It was designed by the CPN Tools1https://cpntools.org.by which the model can be executed(animated by firing transitions and token movements).The code on the left side of the figure shows definitions of functions and variables.2There are two files(for 2DULV and PFV)with the extension of.cpn at the following link showing our original Petri-net models, which can be browsed and executed by CPN Tools.https://drive.google.com/drive/folders/1qGH6k2nQi-SWlT-XQWsUxj6xAmVS UzGs?usp=sharing.Table 8 shows the results of our proposed model based on the two reasoning methods explained in Section 4.2,where the results for the two methods are close to each other.Column ‘Variable values and mode’shows values of five variables(a token)in modes normal(previous mode) and attack (current mode), when the corresponding attack in column‘Attack name’occurs.Two last columns show the results of the two methods of resoning.3Figures of the Secure Water Treatment system model and its Petri-nets as well as the tables related to the attacks are available at the following link.https://drive.google.com/drive/folders/1qGH6k2nQi-SWlT-XQWsUxj6xAmVSUzGs?usp=sharing.Now,we deal with the analysis of attacks based on results in Table 8.

• Pipe burst attack.The results for this attack show(a) based on the PFV, this attack occurs with the truth degree(0.854,0.144),which is an extremely high probability and(b)based on the 2DULV, this attack occurs with the truth

T A B L E 7 Mode transition table for the attacks against the secure water treatment system.

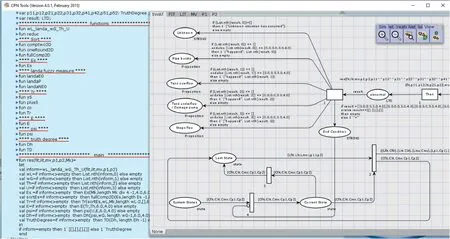
F I G U R E 1 2 A part of our Petri-net model for 2DULV in the CPN Tools environment.

T A B L E 8 Results our proposed model based on the two reasoning methods explained in Section 4.2.

5.3 | Validation of our results by comparing with the previous work

To show the validity of our results, we applied our model to the two scenarios mentioned in Ref.[4] and compared our results with those of Ref.[4].In Ref.[4], we used hierarchical coloured fuzzy Petri-nets for specifying and verifying a cardiac pacemaker.In this section, we apply our current proposed method to the two scenarios stated in Ref.[4].We first create equivalent and compatible coloured tokens for our current method and then compare the results obtained by applying the PFV and 2DULV with the results in Ref.[4] in terms of the truth degree.In Ref.[4], five variables AGE, BMI(Body Mass Indicator), AC(Activity), EMO(Emotion), and BP(Blood Pressure) for a heart patient are considered, which are monitored by the heart pacemaker device.Scenario 1 in Ref.[4]considers an 11 year-old cardiac with BMI=35 and AC=11,where there exist two membership intervals, for AC = 11(Figure 13)with some overlap;therefore,two coloured tokens are considered for the patient.For this scenario,the method in Ref.[4]determines the normal mode for the patient's heart rate two times,one time with a probability of 0.3 and another time with the probability of 0.7 (Rows 1 and 2 in Table 9).

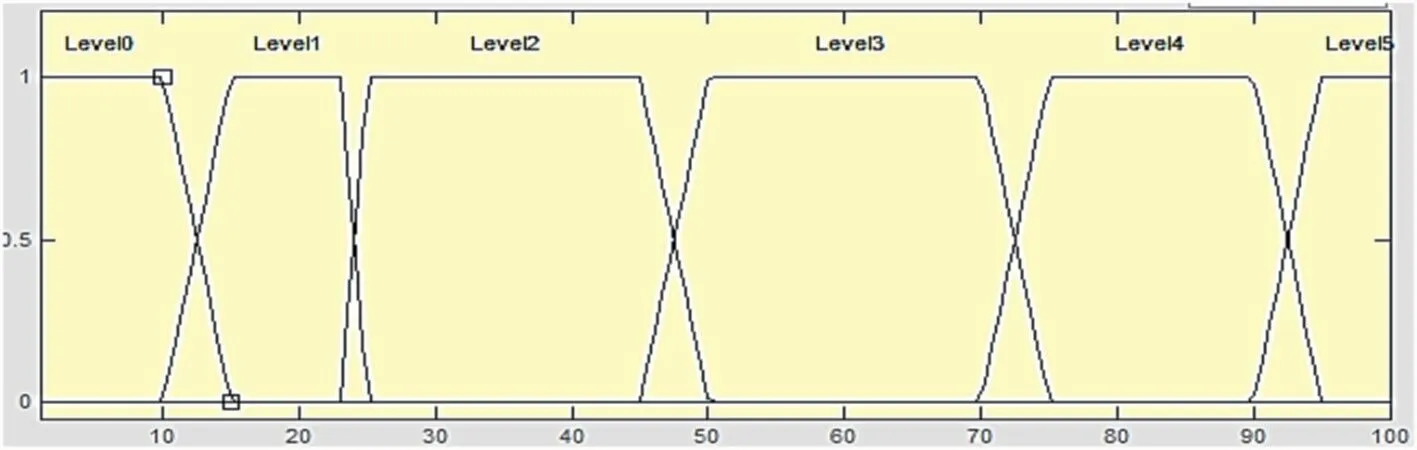
F I G U R E 1 3 AC membership for the first scenario in [4].

Rows 3–4 and 5–6 in Table 9 show the results obtained by performing our reasoning processes based on the PFV and 2DULV,respectively.For both our proposed coloured tokens,both the reasoning methods determine the normal mode.For the former reasoning method, the heartbeat status is determined in the normal mode with the truth degree(0.821,0.181)and (0.762,0.26), indicating a very high probability.For the latter reasoning method, the results of the process for two coloured tokens are almost the same.Values 0.821 and 0.762 in column “Result” of rows 3–4 in Table 9 are close to the corresponding value in row 1 (i.e., 0.7).Moreover, intervals[3.93,5]and[3.56,5]in column“Result”of rows 5–6 in Table 9 denote between before high and very high, which is close to 0.7 in row 1.

Scenario 2 in Ref.[4] considers a 20-year-old cardiac with BMI = 33, taking aerobic exercises (i.e.AC = level3) under stress (EMO = stress), where a coloured token is considered for the patient.After applying the reasoning process in Ref.[4],it determines the heart rate as the normal state with a probability of 1(Column“Results”in Row 1 in Table 10).Rows 2–3 in Table 10 show our defined coloured token, which is equivalent to the token in Scenario 2 in Ref.[4]and compatible with our proposed model.Our model based on reasoning by the PFV (Row 2 in Table 10) shows the normal mode in interval “extremely high” (0.85,0.15), which is equivalent to the result of the reasoning process for Scenario 2 in Ref.[4].Moreover, our model based reasoning by 2DULV (Row 3 in Table 10) shows the normal mode in interval “high and very high” ([4.17,5.0,2.25,4.0]).

According to the coloured tokens defined in both scenarios, the results obtained from PFV and 2DULV are almost close to those of Ref.[4];however,the results based on PFV is more accurate than those of 2DULV.

6 | CONCLUSION

In this research, we introduced a model based on hierarchical coloured fuzzy Petri-nets to overcome the problems (representation and inference when there exist many rules and variables and other fuzzy Petri-nets not considered).Using two reasoning methods, PFV and 2DULV, we did a more precise method.

The previously proposed fuzzy Petri-nets are usually flat and suitable for representing and inferring in case of a small number of rules.However,our proposed model has the ability to visualise and infer systems with a large number of rules and variables, leading to a highly complex system.In addition, by considering cases like the weight of propositions of the rule conclusion, the weight of the premise's propositions, the interaction between the propositions, the threshold value for the premise's propositions, the rule certainty factor, the truthdegree of propositions, and high-level variables, we succeeded to present the system’s uncertainty better and, consequently,we succeeded to do the reasoning process more accurately.

T A B L E 9 Our considered coloured tokens to scenario 1 in [4].

T A B L E 10 Coloured tokens for scenario 2.

Furthermore, by representing the system behaviour using the Mode Transition Table and mapping it to our proposed model, we provided a suitable solution for the vital systems that are constantly changing.Finally,we applied our model to a real-world experiment(behaviour of a Secure Water Treatment System against attacks) and compared the results of two reasoning methods of PFV and 2DULV.The results obtained for both methods were close to each other.

To show the validity of the results produced by our proposed model,we applied the model for the two scenarios used in our previous work and compared the results with those of the previous work.It was shown that the results of our two reasoning methods were almost the same as those of the previous work.However,for both scenarios,the results of the reasoning method based on PFVs were closer to those of the previous work.

For future work, (a) the Mode Transition Table may be considered as multi-mode and then mapped to a hierarchical fuzzy coloured Petri-nets, (b) the model may be extended for multi-stage multi-point attacks,(c)the model may be extended to have the ability to process reasoning based on successive rules and(d)cases like the rule CF and the threshold value for propositions of the conclusion part may be considered, (e)because different combinations of system features may lead to an abnormal state,the accuracy of our presented model can be improved by considering the correlation between the combinations, and (f) the conditional probabilities may be included in the proposed model.

ACKNOWLEDGEMENTS

This article is supported by University of Kashan, (Grant/Award Number: '234333').CONFLICT OF INTEREST STATEMENTNone.

DATA AVAILABILITY STATEMENT

The case study data and specifications are openly and fully available in a public repository that its link was cited in the paper.

ORCID

Mina Chavoshihttps://orcid.org/0000-0002-5422-6887

Seyed Morteza Babamirhttps://orcid.org/0000-0002-1645-4002