连续切换轮系下变尺寸物料的传输模型与路径规划

唐炜 孙宇 顾金凤 陈远

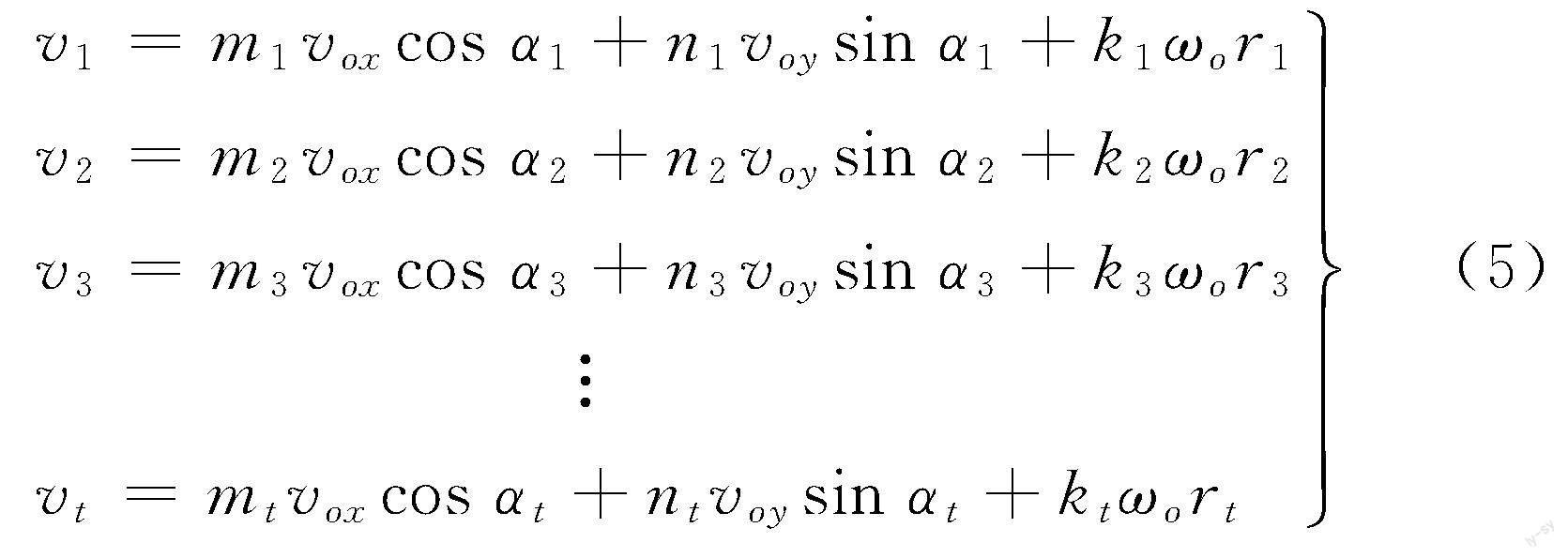
摘要：传统物流设备大多存在传输方式单一、线路柔性调整困难等问题。面向一种呈蜂窝状布局形式的模块化物料传输平台，在三轮模型与牛顿欧拉动力学的基础上，基于全向轮系分别推导了适用于变尺寸物料传输的运动学通用模型与动力学通用模型，以确保传输的准确性和平稳性。将融合生成的改进势场蚁群（IACSPF） 算法用于物料传输路径规划，提高了算法收敛速度并能避免陷入局部最优。最后通过仿真及实验对不同尺寸物料的传输轨迹、速度及路径规划进行了验证分析。研究结果表明，变尺寸物料能以最优路径稳定地传输至目标点附近，轨迹与速度均值的相对误差分别小于4.27%和8.33%，规划路径的长度、时间及拐点数优化率分别为20.77%、55.39%、73.33%，且安全距离较大，验证了所建通用传输模型的合理性以及IACSPF算法的有效性。

关键词：物料传输平台；变尺寸物料；通用传输模型；路径规划；改进势场蚁群算法

中图分类号：TP23；TP391

DOI：10.3969/j.issn.1004132X.2023.11.013

Transmission Model and Path Planning of Variable-size Materials in

Continuous Alternate Wheel Systems

TANG Wei SUN Yu GU Jinfeng CHEN Yuan

School of Mechanical Engineering，Jiangsu University of Science and Technology，Zhenjiang，

Jiangsu，212100

Abstract： Most of the traditional logistics equipment had problems such as single transmission mode and difficulty in flexible adjustment of transmission lines. For the modular material transmission platform with honeycomb layout， based on the three-wheel model and Newton-Euler dynamics， general kinematics and dynamics models for the variable-size material transfer were respectively derived on the basis of the omni-directional wheel systems to ensure the accuracy and smoothness of the transfer. An IACSPF algorithm generated by fusion was used for material transmission path planning， which improved the convergence speed of the algorithm and avoided falling into local optimization. Finally， simulations and experiments were carried out to verify the transmission trajectory， speed and path planning of the different size materials. The results show that the variable-size materials may be stably transported to the vicinity of the target by the optimal path. The relative errors of trajectory and speed average are less than 4.27% and 8.33% respectively. The optimization rates of the length， time and number of turning points of the planned path are 20.77%， 55.39% and 73.33% respectively， and the safety distance is larger， which verifies the rationality of the proposed general transmission model and the effectiveness of the IACSPF algorithm.

Key words： material transmission platform； variable-size material； general transmission model； path planning； improved ant colony system with potential field（IACSPF） algorithm

0 引言

近年來，许多传统制造型企业为了实现提质增效的目标，正逐步向数字化、网络化、智能化方向发展。但仅仅关注企业生产效率是不够的，大批量货物如何通过社会物流进行高效便捷的仓储、运输和配送也应得到足够重视。此外，随着电子商务的蓬勃发展以及新冠疫情的持续影响，越来越多的消费者选择网上购物［1］，造成快递包裹的日均数量显著增加。传输与分拣是仓储物流中心的核心业务，一般要投入一半以上的人力，其作业速度及出错率会直接影响物流中心的工作效率及顾客的满意程度。相比传统的人工［2］或半自动［3］分拣方式，物料传输领域需进一步提高自动化程度，提升自身的灵活性与适应性［4］，以便更加高效、准确地分拣包裹［5］。而实际上，在物料传输的整个过程中为了寻求最佳的分拣策略与缩短分拣时的传输路径，消耗了大量的人力与时间［6］，因此，传输系统的机械结构以及物料传输的路径规划都值得深入研究。

目前，国内外许多学者对物料自动化传输分拣系统或其路径规划进行了相关研究。YANG等［7］考虑到不同卷烟的差异性，设计了一种夹点式异型卷烟分拣机构，提高了设备的分拣效率，更有利于自动化管理，但该设备占地面积较大且无法移动，分拣物料相对单一，环境适应性不高。LIU等［8］提出了一种基于STM32的物流分拣小车，小车上安装有机械臂以实现货物的抓取功能，但物流小车货物运输量较小且机械臂的抓放与定位精度要求较高，不适用于大规模物料的运输。KAUFMANN公司［9］研制了一款名为MoveFlex的无电力可任意伸缩、变形传输带，可根据用户需求随意调节长短和形状，使货物能在传输带上靠重力分量自行滑动而无需任何电力，但该传输带只适用于运输小尺寸包裹的仓库，对于运送较重货物，可能会因传输过程无法控制而造成货物跌落，存在一定的安全隐患。LIU等［10］以人机工程学为基础，对托盘分拣設备进行了优化，提高了分拣效率与工作人员的操作舒适性，但仅对传送带的结构进行优化，并没有改变人工或半自动的本质分拣方式，仍有较大的改进空间。杨伟国［11］研究了一种基于全向轮的可编程输送平台，解决了中小型物流企业对大型自动分拣设备的需求问题，但平台中各模块由4个相互呈90°分布的全向轮构成，结构设计存在一定局限性，使得物料的分拣路径为基本的直线传输，若遇到障碍物时可能无法及时躲避。CLAUDIO等［12］提出了一种名为Celluveyor的智能传送带，可对指定货物进行传输、码垛及卸垛，改变了传统物料的传输方式，分拣灵活性得以显著提升，该系统虽为模块化设计，但在各模块与平台接触位置仍采用固定连接方式，不便于维护；该研究的重点是视觉对物料的识别、跟踪与反馈功能，且实验中采用的是具有相同尺寸的物料，未涉及不同尺寸物料传输模型及路径规划方面的研究。高振清等［13］设计了一种全向轮物流搬运设备，并对其进行了运动学分析建模，保证了全方位的移动特性，但建立的数学模型仅适用于三个全向轮组成的机构，模型本身不具备通用性，且考虑到运输平稳性，其动力学方面存在一定欠缺。ZAHER等［14］提出了一种基于强化学习的全向轮输送机的路径规划与分拣方法，能自动引导不同类型的包裹到达各自的目的地，无需使用传统的控制方法，并对算法的合理性加以验证，效果良好，但实验环境较为简单，算法在复杂环境下需要较长的训练时间，可能导致无法快速收敛。LUO等［15］在路径规划中，通过引入最优解与最差解、动态惩罚等方法改进了传统蚁群算法，收敛速度有所提高，但未对局部路径中存在障碍物的情况进行深入研究，全面性稍欠缺。李颀等［16］采用改进的A*算法与人工势场法完成多全向轮分拣平台的路径规划，全局与局部路径皆有优化，物料传输位置误差较小，但路径轨迹的平滑度有待提高，仍可进一步减少能量损失。杨莹等［17］提出一种基于改进快速搜索随机树算法的包裹分拣路径规划，包裹的传输速度得到了显著提高，但其仿真分析为理想状态下，未涉及包裹传输过程中动力学方面的研究，实际场景下的传输稳定性需要深入考虑。

在分析以上不足的基础上，本文面向一种模块化的物料传输平台，对连续切换轮系下变尺寸物料的传输情况进行了运动学和动力学建模分析。相比文献［7-9］，本平台整体具有模块化、蜂窝状的结构特征，可根据实际需要进行拼接扩展，安装位置灵活，提高了环境适应性，并通过增加同时传输的物料数量来满足大规模输送的需求，且传输物料的尺寸与质量受限制较小。相比文献［10-11］，本研究改变了传统单一方向的固定线路传输方式，可在不改变平台机械结构的前提下柔性地调整物料的传输路径，如某单元模块出现机械故障时，可利用平台全方位传输的特点来高效地变更可传输的路径。相比文献［12］，本平台采用Z形连接件上的卡槽完成各模块的固定安装，无需螺栓连接，插拔方便，避免了螺栓松动而导致平台不稳定的情况，也便于日常维护；各模块控制器作为子节点挂载于CAN总线与上位PC机组网通信；着重研究了不同尺寸物料传输时的通用模型及其路径规划，有效拓展了平台的应用场合。相比文献［13］，本研究的运动学模型具备一定的通用性，而不仅限于四轮接触式传输，且考虑到传输平稳性，推导出了一种具有普适性的通用动力学模型。相比文献［14-17］，本文考虑到工作中轮系可能存在突发局部故障的现象，采用了一种改进势场蚁群（improved ant colony system with potential field，IACSPF）算法，可自主动态调整物料的优化传输路径，提高了算法的收敛速度，并避免易陷入局部最优的情况；拐角过度处较为平滑，整体传输路径轨迹更加贴合工程实际。最后，本文对不同尺寸物料的传输情况进行了仿真分析与样机测试，结果表明，传输过程中物料的轨迹、速度误差在合理的范围内，路径规划算法相比改进前具有自身的优势，总体上可确保物料传输的准确性、稳定性及传输效率，从而验证了针对模块化传输平台所建运动学和动力学模型的合理性与IACSPF路径规划算法的有效性。

1 传输系统布局及平台结构

1.1 传输系统整体布局

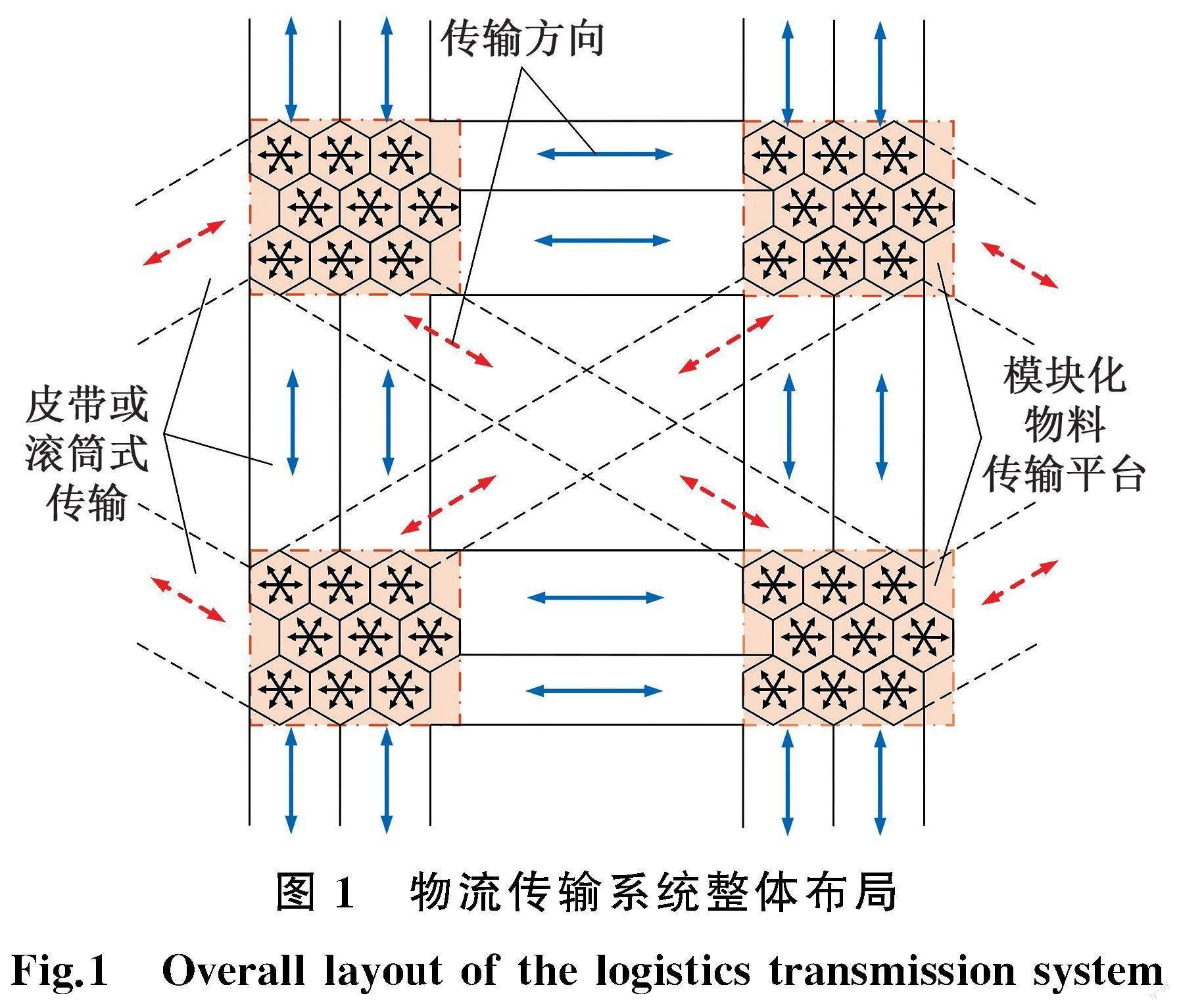
物流传输系统一般由控制装置、分类装置、输送装置及分拣道口等组成。对于其中的输送装置，传统物流传输系统通常存在以下不足：传输方式大多固定，一般采用皮带式或滚筒式的传输形式；传输线路及方向大多单一，当需变更路径时，柔性调整困难；若出现局部机械故障，可能会导致整个系统运行停顿甚至瘫痪。本文所采用的模块化物料传输平台在整个物流传输系统中，主要处于传统传输通道的中间节点位置，起到线路切换、中转过渡等中间枢纽的作用，从而在不改变传输系统机械结构的前提下，可实现对传输路径的柔性调整。图1为物流传输系统的整体布局示意图，其中，矩形边框表示传统的物流传输通道（如皮带式或滚筒式），若干呈蜂窝状布局的正六边形单元模块构成了本文所述及的模块化物料传输平台，箭头表示物料的可传输方向。

采用上述布局的物流传输系统，物料在经过传输平台时，可实现全方位传输，用户能根据实际工程需要灵活地设置入/出口通道。图2描述了不同类型传输设备所实现的不同传输效果。

1.2 平台结构说明

模块化物料传输平台由若干个正六边形单元模块构成，整体呈蜂窝状的布局形式。每个模块体由Z形连接件固定在平台上，表面嵌入式安装3个在圆周方向上呈120°均匀分布的全向轮，且任意3个相邻全向轮的几何中心组成尺寸完全相同的等边三角形。图3为物料传输平台的结构示意图。

相比于传统物流传输设备，该传输平台除了可实现全方位传输以外，还具有以下特点：

（1）机械结构可细分至最小单元模块，平台大小可根据实际需求进行删减或拓展。各模块体具有互换性以及即插即用的特征，便于后期维护。

（2）在不改变机械结构和控制系统的前提下，该平台能柔性地调整物料传输路径，且可主动避开故障区域，不会造成整个传输系统工作瘫痪，控制系统鲁棒性较强。

（3）传输路径外的无关轮系在不工作时处于休眠状态，降低了平台能耗；在传输过程中，各轮系与物料间的滚动摩擦力较小，传动效率高。

2 变尺寸物料运动学分析

运动学特性是对机械系统工作原理的本质表述。为了实现物料在平台上的全方位传输，在建立物料运输的运动学模型前，特作以下假设：

①各全向轮系结构参数完全相同，且各轮顶点所处高度一致形成共面；

②物料底面平整，在传输过程中至少与3个全向轮保持接触；

③物料底面与全向轮之间具有充足的摩擦力，无打滑现象。

2.1 坐标系建立

物料传输平台坐标系的建立如图4所示，其中涉及三类坐标系，具体如下：

（1）世界坐标系OXY。世界坐标系是基于平台建立的全局坐标系，其原点位于整个平台左下方的角点位置，用于表示物料的移动轨迹。

（2）局部坐标系oxy。局部坐标系的原点位于物料的几何中心，可用于表示物料的移动方向。

（3）轮子坐标系oixiyi。轮子坐标系的原点位于各全向轮的几何中心，可用于后续传输模型的建立。

图4中，虚线表示物料的轮廓，点A、B、C为全向轮与物料的接触点。为使图面简洁，后续文中的局部坐标系、轮子坐标系及接触点不再标明。

2.2 基本三轮运动学模型

先考虑传输过程中仅有三个全向轮与物料始终接触的情况。图5为三轮接触下的物料传输平台运动学分解示意图。

单个全向轮的线速度vi（i=1，2，3）是由物料几何中心的速度矢量vo及角速度矢量ωo共同作用而合成的结果，可表示为

vi=|vo+ωo×ri|（1）

其中，vo=vox+voy，vox、voy分别为vo在坐标轴x、y上的速度矢量分量值；ri（i=1，2，3）为仅三轮接触物料时，点o到各轮子经过接触点后的切线li的垂直矢量距离。

将式（1）细化到每个全向轮各自vi的方向上，且因各轮涉及的矢量方向已相同或相反，故下文参数均转化为标量形式进行模型构建，可得

式中，vox、voy分别为vo在坐标轴x、y上的速度分量值；θ为物料运动方向与x轴的夹角；αi为切线li与坐标轴x的夹角，取αi為π/6或π/2。

进一步地，可得

式中，ωi为第i个全向轮的转动角速度；R为全向轮（等效）半径。

将式（3）改写成矩阵形式，可得逆运动学模型为

式（4）描述了物料仅与三轮接触时，各全向轮角速度与物料传输速度之间的关系。这在理论上表明：仅三轮接触的物料能在平台上进行全方位传输。

2.3 连续切换轮系运动学通用模型

前述三轮运动学模型只适用于传输时物料仅与三轮接触的情况，并不具备通用性。对于物料传输平台，输送的物料尺寸应尽量不受限制或受较小限制，才能满足仓储物流业的工程化需求。当物料尺寸发生变化时，所接触的全向轮数量也将变化，无可避免地会涉及到多模块协同控制、多轮系连续切换，即三轮、四轮甚至更多轮协同传输的情况。另外，在物料传输过程中，即使出现相同轮子数量作用的情况，各全向轮的排布方式、具体位置也可能不尽相同。故在物料传输平台上，分析推导一种适用于变尺寸物料进行全方位传输的运动学通用模型具有重要的现实意义。图6表达了四轮接触时所存在的三种不同轮系布局情形。

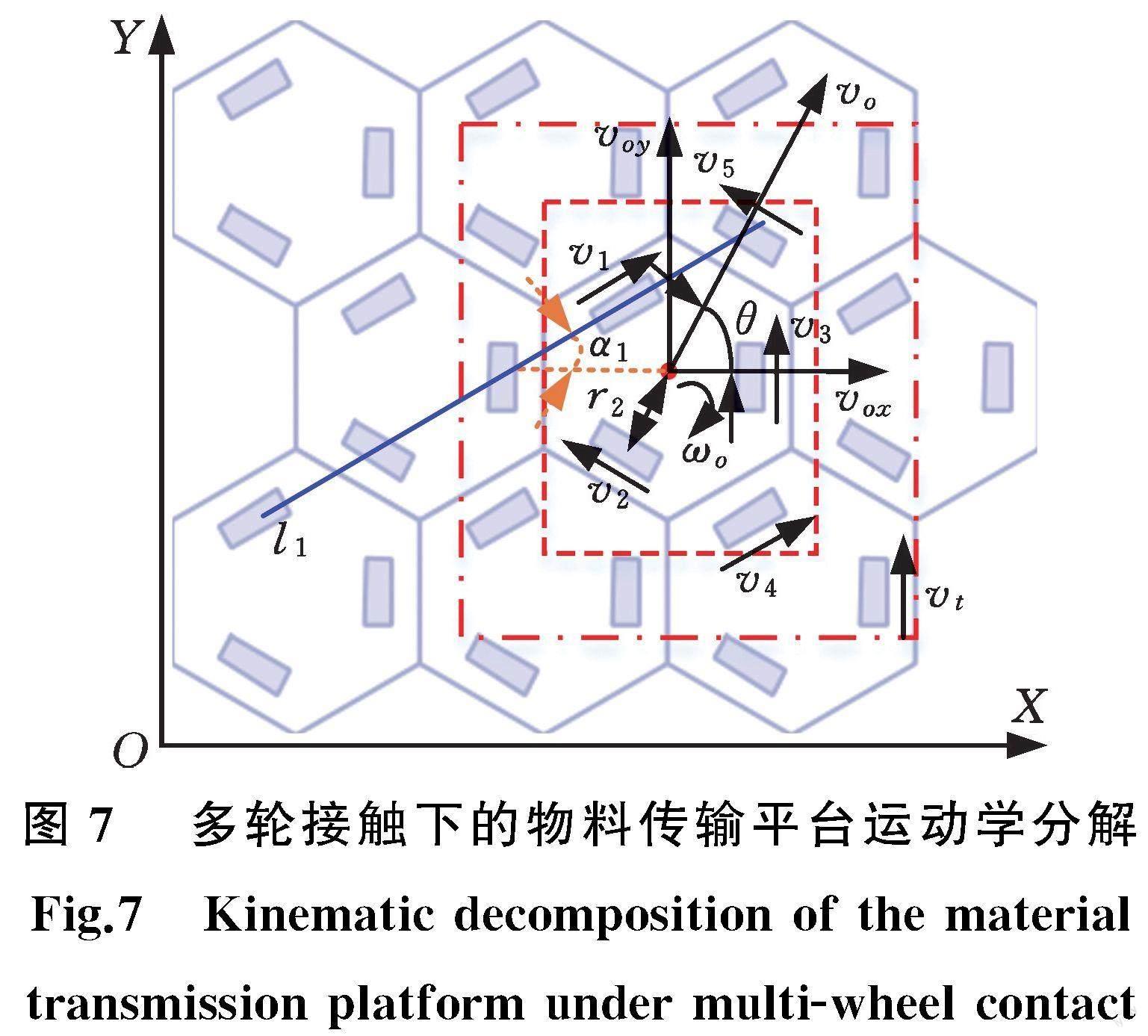
在连续切换轮系下，具体的运动学解算示意图见图7，其中虚线与点划线表示不同尺寸的物料轮廓。

理论上，随着物料传输平台的无限扩展，物料的尺寸也可任意增大，所接触全向轮的数目也相应增加。记物料接触的轮子最大数目为t（t≥3），参考图7所示的运动学分解与式（1），并引入mj、nj、kj等系数来构建方程，可得出各全向轮线速度与物料运动参数的关系：

其中，j=1，2，…，t；mj，nj=±1；kj为rj的比例系数，其正负由各轮参考ωo的旋转方向所定。

将vj=ωjR关系代入式（5），并转化成矩阵形式，则得到连续切换轮系下的变尺寸物料传输逆运动学通用模型，具体为

将式（6）中的系数雅可比矩阵记为Tj，简化模型为

［ω1 ω2 ω3 … ωt］T=Tj［vox voy ωo］T（7）

当物料在传输平台上运动时，若矩阵Tj不满秩，则物料传输会存在奇异点，因缺少部分自由度而无法实现全方位移动。对于本平台，当物料接触的全向轮存在与图5中虚线包围的三轮排布相类似布局形式时，Tj则列满秩，物料可实现全方位传输。

Tj中mj、nj的取值会影响到各全向轮的转向，对保证物料的全方位平稳传输具有重要作用，具体取值规律如表1所示，其中L1（±）表示在与1号全向轮相同排布方式的轮子中，线速度与v1的方向相同或相反，L2（±）与L3（±）的意义类似。

3 变尺寸物料动力学分析

运动学主要分析物料在传输过程中运动曲线与时间之间的关系，并不参考使运动产生的力与力矩。而对物料传输平台来说，仅从物料输送的运动学方面思考不够全面，不能充分解决各全向轮所受来自物料的摩擦力和外界因素对平台运动控制的干扰。故建立一种以变尺寸物料为背景的多轮动力学通用模型，这将有助于该问题的分析解决。

3.1 摩擦力的确定

平台上的每个全向轮由整体主动轮（轮毂和辊子）和局部从动轮（辊子）组成，主动轮转速由直流电机进行闭环控制，而从动轮由接触物料时产生的摩擦力驱动。为便于动力学模型的建立，在不考虑环境温度、从动轮滚动时弹性形变与磨损的基础上，确定各全向轮主动轮、从动轮与物料接触时产生的摩擦力Fgj、fgj，具体为

式中，μ、M、g分别为滚动摩擦因数、物料质量及重力加速度。

3.2 连续切换轮系动力学通用模型

多轮接触下的物料传输动力学分解如图8所示，其中Fj为第j个全向轮所受的电机驱动力。

记传输物料在全局坐标系OXY下的位姿为p=（X，Y，θ）T。根据牛顿欧拉动力学方程，将力在坐标轴上进行分解，可得

结合图8所示的动力学分解，将相关参数代入式（9），可得

其中，εj=±1，与各全向轮的转动方向相关；τX，τY=±1，与物料运动方向有关；mj、nj与表1中的取值规律相同。

将式（10）转换成标准形式，得

尽管不同物料传输平台的机械结构、相关参数及传输物料的尺寸会有所不同，但式（11）所示的动力学模型［18］皆存在以下性质。

（1）正定性。平台的惯性矩阵H对物料任意时刻下的位姿p都是正定对称的，即对于任意n维非零向量x，有xTHx>0。

（2）有界性。H对任意p都是一致有界的，即存在正数σ1、σ2，使得0<σ1I≤H≤σ2I，其中I为单位矩阵。

4 物料传输路径规划

前述运动学/动力学通用模型可用于保证不同尺寸的物料在模块化传输平台上实现准确、稳定的全方位传输。而物料传输路径的长短是衡量该类平台工作效率的重要指标，在运动学/动力学模型的基础上，分析物料传输的路径规划问题，有利于提高物料的传输效率，减少不必要的能量损耗，且更贴近工程实际应用。考虑到传统蚁群算法（ant colony optimization，ACO）存在收斂速度慢［19］、易陷入局部最优［20］以及人工势场法（artifificial potential fields，APF）目标不可达等问题［21-22］，分别对两种方法进行改进并融合，最终采用IACSPF算法完成物料的路径规划。

4.1 改进蚁群算法

4.1.1 优化启发函数

通过引入下一节点b与目标点D之间的距离dbD以及动态权重系数对原启发函数进行优化，以提高收敛效率，具体为

其中，η′ab（t）表示改进后的启发函数，a为当前节点；B为平台的总模块数量，Bk为当前迭代次数k中最短路线涉及的模块数量。动态权重系数λ1、λ2存在λ1+λ2=2的关系，两者初始值为1，且当Bk增大，λ2的数值随之增大。

4.1.2 因子自适应更新策略

ACO算法的信息素启发因子α0、距离期望函数因子β0及信息素挥发因子ρ0是常量，但由于前期路径上信息素含量少，地图信息不全，蚁群勘探的盲目性强；而后期又考虑到信息素累积过多，信息素浓度较高，最终局限了蚁群的搜寻范围，易产生局部最优情况。可见，不变因子的设定不利于最佳路径的搜寻，需采用一种因子自适应更新策略，具体为

其中，K为算法总迭代次数；u0、u1、u2为常量且大于1；α′、β′、ρ′为各因子改进后的表示参数，其变化曲线见图9。

在迭代初期，为使蚁群尽可能探索较多路径，α′与β′的变化幅度较小、变化速度较慢，前者权重占比较小，后者权重占比较大，以保证β′重要程度；ρ′在自身取值范围内应取较大数值，有利于增强蚁群的勘探能力。随着迭代次数的增加，α′权重提高，β′权重下降，且两者变化的幅度与速度都逐渐增大；ρ′数值逐渐减小，负反馈效果减弱，信息素浓度也随之提高，加剧了信息素浓度对路径搜寻的影响程度。在一定迭代次数后，蚁群会将信息素浓度最高的路径作为最优路径。因此改进蚁群算法（improved ant colony optimization，IACO）可降低蚁群寻路的随机性、提高算法收敛速度并减小陷入局部最优的概率。

4.2 改进人工势场法

在APF斥力场模型里通过增设距离调节因子ρNg（ρNg为物料与目标点的距离，其中N为常数）来解决APF的目标不可达问题，改进后的斥力场函数以及合斥力分别如下：

其中，c为斥力增益系数；ρ为障碍物作用的最大距离；ρ（q，q0）为物料当前位置q和障碍物位置q0之间的距离；grad（ρ（q，q0））表示梯度函数；斥力Freq1、Freq2的方向分别为从障碍物指向物料和从物料指向目标点，具体见图10。

当引入了ρNg后，会使得传输过程中作用在物料上的引力Fatt与合斥力Fareq的大小在一定程度上减小，且仅在物料到达目标点的位置时，两者才会同时减小为零，此刻目标点为最小势能点，物料将无法移动，进而解决了目标不可达的问题。

4.3 IACSPF算法路径规划

虽然IACO算法能规划出一条全局最佳路径，但当与障碍物距离较小时，可能无法及时避开或出现转角过大情况；而改进人工势场法（improved artifificial potential fields，IAPF）单独路径规划时虽能有效避开障碍物，但由于全局路径信息的匮乏，规划的路径一般不是最佳的。故需对IACO和IAPF两者进行算法融合，生成一种IACSPF算法完成路径规划，以进一步提高物料的传输效率，并减少拐点数目，平滑传输路径。

IACSPF算法的流程如图11所示，具体步骤如下：

（1）在全局路径规划中，采用IACO算法规划路径。

（2）记录路径中各拐点与目标点的位置，并将目标点作为最后一个拐点，按顺序生成拐点位置集合Di。

（3）计算集合Di中相邻两拐点间的距离dmin，并判断是否满足dmin≤10 cm。若是，则删除前一拐点，并更新拐点位置；否则直接更新拐点位置。

（4）采用IAPF方法进行局部路径规划，并将记录的拐点作为局部路径中的子目标点。

（5）判断局部路径的终点是否与目标点的位置相同，若是，则输出融合算法IACSPF规划的最佳路径，否则返回步骤（4）。

5 仿真分析

物料的传输轨迹描述了物体的运动位置，传输轨迹与期望轨迹的吻合程度是评判运动学模型是否合理的主要依据。在动力学方面，运动速度的变化会涉及到力的控制，故采用物料的传输速度作为评判通用动力学模型是否合理的指标。本文搭建了“MATLAB+ADAMS”的联合仿真实验平台，并通过物料的传输轨迹与传输速度验证连续切换轮系下变尺寸物料的通用数学模型的合理性与有效性。此外，分别在14×20栅格的复杂环境和15×15栅格的模拟实验环境下，对改进路径规划算法的优越性进行了实验验证。在此设定LXδ、LYδ、LZδ为各轴向上的位移，vXδ、vYδ、vZδ为各轴向上的速度分量，其中δ为路径序号。表2所示为物料传输平台的相关仿真参数。

5.1 传输轨迹仿真

物料A在传输过程中始终且仅与3个全向轮接触，设定的期望传输路径为路径1（沿X轴向）。对于物料B，为验证前述模型的通用性，规划了3条期望传输路径（沿X轴向、沿Y轴向、沿S形曲线）。上述所有期望路径如图12所示。

5.1.1 直线传输

直线传输仿真情况下，物料在3条路径上的期望位移如表3所示。仿真后各路径上的轨迹曲线及其误差如图13所示。分析图13a～图13c可知：物料预期运动方向上的位移LX1、LX2、LY3在0～0.3 s较缓慢地增大，这是由于控制信号发出后，各全向轮的驱动电机存在一个“启动—加速”过程，而在0.3～6 s，位移与时间成线性比例关系，无突变；其余各轴向上的位移近似于一条直线，无明显波动。由图13d可知：路径3上的轨迹误差相对稍大，这是由于相比于路径1、2中物料仅与三轮/五轮进行接触，路徑3则涉及到四轮、五轮接触以及多轮模型间的相互切换问题，情况相对复杂，但总体来看各路径的轨迹误差均小于1.5 cm，路径1、2、3的相对误差分别为0.9%、1.66%、3.13%，能准确将物料送至目标点附近。

5.1.2 曲线传输

沿S形曲线传输的路径4是由四段曲线拟合而成的，其中函数Y1～Y4分别对应图12d中0→1、1→2、2→3、3→4四段曲线，具体的表达式分别如下：

物料B在路径4上仿真后的轨迹曲线及其误差如图14所示。分析图14a可知：LX4总体呈下降、上升再下降的趋势，除在拐角过渡的时间段变化较缓慢外，其他时刻下的变化率较明显且大致相同；LY4总体呈下降趋势，但在2.2～5.2 s、9.7～12.7 s的变化率较大，分别对应图14b中的1→2、3→4两段曲线；LZ4整体较平稳，无明显波动现象。由图14b可知：仿真轨迹与期望路径大致相符，但在拐角1、3、4处误差相对明显，这是由于此处物料传输转角较大，各全向轮转速变化明显，个别轮子转向也发生改变，物料的惯性与摩擦力等因素影响了传输路径的吻合度；此外，随着时间的增加，传输轨迹偏差逐渐累积，使得轨迹末端不可避免地会存在一定误差。由图14c可知：当物料沿S形曲线传输时，由于模型较复杂、切换频繁且存在若干拐角，使其轨迹误差略大于前述直线传输误差，但能控制在5 cm以内，最大相对误差为2.3%，仍可将物料有效传输至目标点附近，从而验证了通用运动学模型的合理性。

5.2 传输速度仿真

在物料能够满足期望轨迹传输的前提下，还需对各坐标轴方向上的传输速度进行仿真，以分析物料的传输效率及其稳定性。

5.2.1 直线传输

物料沿前述三条直线路径进行传输时，各轴向速度的仿真变化曲线见图15，可以看出：物料在预期运动方向上的速度分量（vX1、vX2、vY3）在0～0.3 s内逐渐增大，并在达到期望速度后保持匀速传输且波动较小，而其余轴向上的速度分量围绕在速度为0 附近上下波动，主要由于物料受到轮子因微小形变而产生的应变力作用，使传输速度发生了一定变化。具体仿真结果见表4，其中忽略了0～0.3 s间的启动加速阶段。

由表4可以看出：各轴向速度的仿真均值误差较小，最大为0.24 cm/s；而由于全向轮对物料产生的驱动力处于OXY平面内，Z轴方向只有较小的应变力，因此vZ1、vZ2、vZ3的方差分别略小于vY1、vY2、vX3的方差。

5.2.2 曲线传输

物料B在路径4上仿真后的速度变化曲线见图16。分析可知，因传输过程中X轴正负方向均有位移，故vX4会在-15 cm/s、0及15 cm/s各保持一段时间后进行变化；而Y轴仅负方向有位移，故vY4小于0且在0与-8 cm/s之间进行变化；vZ4始终在速度为0 附近小幅波动。此外，图16中的矩形虚线框表示该路径中的4个拐角处，期望路径中此处vX4、vY4的变化应从同一时刻开始，但实际仿真中的变化时刻略有不同，这与拐角处轨迹误差产生的原因相同。由于S形路径的特殊性，vX4、vY4速度存在方向性，具有较大变化，在此不作比较；而vZ4仿真均值为0.59 cm/s，方差为2.2 cm2/s2，速度曲线波动幅度较小。

综上，物料传输时的仿真均值速度与其期望速度相比，误差值较小，平台能保证物料较平稳地传输，从而验证了通用动力学模型的合理性。

5.3 路径规划仿真

5.3.1 复杂环境

物料传输时共设定了4条路径，其中前3条为直线传输，模型切换与路径规划较为容易，为体现IACSPF算法的优越性，在S形路径（即路径4）的基础上进行了算法的对比分析。其中，搭建了14×20的栅格化地图环境，并设定物料的起点、目标点及工作轮，单个栅格长度为5 cm，且规定物料质心只能在本栅格周围的8个相邻栅格内传输，仅图17中的黑色栅格是人为设定的物料质心路径不可经过区域。改进前后的路径规划算法对比结果如图17所示。

分析图17a、图17b可知，采用ACO算法规划的路径拐点较多且部分转角过大，不符合物料传输的路径最优要求；采用IACO算法规划的传输路径较短，且拐点数目少，可提高物料的传输效率，但仍存在转角较大的问题；而当引入IAPF与IACO算法融合后，形成的IACSPF算法可使路径拐点明显减少，规划路径较为平滑，更加符合实际工程应用。

由于IACSPF是在采用IACO进行路径规划时就已完成迭代收敛，然后将IACO中的拐点作为IAPF的子目标点进行算法融合，因此在分析迭代收敛曲线时，仅需将ACO与IACO进行对比即可。分析图17c可知，ACO收敛曲线的波动幅度较大，收敛速度慢，耗时较长，且达到最终迭代次数后仍未完成收敛，可见产生了局部最优问题；而IACO收敛曲线的波动较小，耗时短，在完成28次迭代后趋于稳定，耗时短，且搜寻到了最优路径。具体对比结果见表5。

由表5还可看出：IACSPF虽比IACO的路径长度与运行时间稍长，但拐点数目明显减少，更符合工程实际需求；而相比于ACO，IACSPF的寻优能力更强，路径长度、运行时间及拐点数目的优化率分别为20.77%、55.39%、73.33%。主要原因在于：规划初期，由于IACSPF中改进了启发函数且ρ′值较大，信息素挥发较快，减小了信息素对未来蚂蚁行为的影响，提高了算法的探索能力；规划中期，各因子由于动态变化，α′权重提高，β′权重下降，ρ′值逐渐减小，加强了信息素浓度对路径选取的影响效果，增强了算法的开发能力；而规划后期，IACSPF也能更快收敛，并搜寻到最优路径。综上，采用IACSPF算法规划路径，可在通用数学模型的基础上显著提高物料的传输效率及其平稳性。

5.3.2 模拟实验环境

由于后续实验样机的模块单元数量有限，为便于对比，本文在15×15的栅格环境下重新定义了起点、目标点及工作轮，并运用IACSPF算法进行路径规划（记为路径5），仿真结果如图18所示，此处的黑色栅格为轮系故障区域。由仿真结果可知：在模拟实验环境下，IACSPF算法规划的路径较为平滑，仅存在两个拐点，能量损失较少。

6 传输平台样机实验

本文搭建了图19所示的实验环境。物料传输系统由传输平台、物料、PC机、工业相机等设备组成。其中，相机用于对传输过程中物料的位置进行视频采集，并将其反馈给PC机以进行闭环控制；传输平台尺寸为100 cm×90 cm，实验栅格设定为7 cm×7 cm。物料A与B的尺寸、质量等参数见前述表2。

6.1 传输轨迹与速度

因平台样机所涉模块的数量有限，故本文仅在路径1、2、3上对不同尺寸物料A与B的传输轨迹进行实验。同时，通过控制物料的不同传输速度来验证平台的工作稳定性。经对模块承载能力、物料传输惯性、轮系电机驱动特性等因素的综合评判，在30～50 cm/s范围内选取一系列期望传输速度进行了传输测试。3条路径下的物料实际传输轨迹及对应误差如图20所示。

分析图20a、图20b、图20c可知，在不同速度下的物料3条路径传输轨迹与预期相符，近似于一条直线，与仿真的结果相呼应，进而能确保物料准确到达目标点附近，其中，各传输轨迹的起始点不相同，主要由于在人为放置物料时会存在一定的位置偏差。由图20d、图20e、图20f可知，随着传输方向位移的增大，物料实际传输路径与预期路径的误差值也逐渐增大，且较小/较大速度对应的误差值稍大，但从整体来看，轨迹误差始终小于2 cm，不同速度下路径1、2、3的最大相对误差分别为1.22%、4.27%、1.93%，误差值较小，符合实际的传输需求。轨迹误差产生的原因主要如下：物料每次放置的位置有所不同；物料本身存在质量与惯性的影响；物料与全向轮接触面存在打滑现象；传输平台加工与装配精度的影响。

由于仿真中速度仅在传输方向上具有一定误差，故实验过程不考虑其他方向上的速度误差，并记vXδ-av、vYδ-av为各路径上的平均速度，下标av表示不同的期望速度值。实际传输平均速度见表6，分析可知，物料的实际传输速度与期望速度大致相符，相对误差较小，最大为8.33%，可见物料传输过程较为平稳，并无窜动现象的产生。

综上所述，當不同尺寸的物料A与B在不同路径上传输时，会涉及到不同的运动学、动力学模型，采用前文建立的通用数学模型，可使物料传输到指定位置附近，偏差较小，并保证了一定的传输稳定性，进而验证了通用数学模型的有效性。

6.2 IACSPF算法路径规划

在实验平台上对采用IACSPF算法规划的路径进行物料传输，将所得到的实际路径与模拟实验环境中的仿真路径进行对比，具体结果如图21所示。

由图21可以看出，平台实测路径与仿真路径的轨迹具有较高的整体重合度，但在物料传输路径的两个拐角处存在一定偏差，这主要因为在实际传输中，转角处涉及轮系多运动模型的切换，而对应电机在实时改变其转速与转向时，不可避免地会存在一定响应延迟，并且物料自身惯性对传输精度也存在一定影响，故造成物料在传输路径拐角处的偏差稍大。

此外，为了确保物料传输的安全性，需对传输过程中物料与障碍物区域之间的间距大小加以考虑。具体做法是：将障碍物边界作为圆心所在位置，从0开始逐渐增大圆的半径尺寸，当圆的轮廓（图21中虚线）与实际路径首次接触时，此时圆心到接触点的距离为最小安全距离。从图21中可以看出，R1、R2为安全距离较小的两个圆轮廓，距离分别约为5.4 cm、7.5 cm，足够物料灵活地避开障碍物区域。

综上，采用IACSPF算法规划的路径在实际传输过程中的轨迹偏差总体较小，可保证物料到达指定位置附近，并且传输过程与障碍物区域存在较大的安全距离，不会发生碰撞现象，从而验证了路径规划算法的合理性。

7 结论

（1）分析推导了在连续切换轮系背景下的变尺寸物料通用运动学模型，确保了物料在平台传输时能达到指定位置，误差较小。

（2）提出了一种通用动力学模型用于变尺寸物料传输，传输过程较为平稳，确保了平台的工作稳定性。

（3）采用改进势场蚁群算法完成物料传输的路径规划，该算法收敛速度快，缩短了路径长度，提高了物料的传输效率。

（4）通过仿真与实验，验证了模块化平台在传输物料时所用运动学和动力学通用传输模型的合理性与改进路径规划算法的有效性。

参考文献：

［1］ KHATIB E J， BARCO R. Optimization of 5G Networks for Smart Logistics［J］. Energies， 2021， 14（6）：1758-1776.

［2］ 李明，吴耀华，吴颖颖，等. 人工与自动化双分拣区系统品项分配优化［J］. 机械工程学报， 2015，51（10）：197-204.

LI Ming， WU Yaohua， WU Yingying， et al. Items Assignment Optimization for Double Picking Zones with Manual Picking System and Automated Picking System［J］. Journal of Mechanical Engineering， 2015， 51（10）：197-204.

［3］ 胡金昌，马文凯，杨栋，等. 考虑客户收货顺序的“货到人”分拣系统的订单排序和客户分批优化［J］. 机械工程学报， 2020， 56（24）：246-253.

HU Jinchang，MA Wenkai， YANG Dong， et al. “Part-to-Picker” Picking System Order Scheduling and Customer Batching Considering Commodities Received by an Orders Sequence［J］. Journal of Mechanical Engineering， 2020， 56（24）：246-253.

［4］ KEEK J S， LOH S L， CHONG S H. Design and Control System Setup of an E-pattern Omniwheeled Cellular Conveyor［J］. Machines， 2021， 9（2）：43-74.

［5］ TAN Zheyi， LI Haolin， HE Xueting. Optimizing Parcel Sorting Process of Vertical Sorting System in E-commerce Warehouse［J］. Advanced Engineering Informatics， 2021， 48：101279.

［6］ GAO Xinyue， LIU Lei. Green Intelligent Logistics Sorting System in Big Data Environment［J］. IOP Conference Series：Materials Science and Engineering， 2020， 711（1）：010240.

［7］ YANG Xudong， MU Kangqi， ZHANG Junhua， et al. Design and Analysis of Sorting Structure of Special-shaped Cigarette［J］. IOP Conference Series Materials Science and Engineering， 2019， 493（1）：012073.

［8］ LIU Le， XIE Jiawen， WU Wenxin， et al. Design of Intelligent Logistics Car Based on STM32［J］. Journal of Physics：Conference Series， 2021， 1952（4）：042102.

［9］ CHEN Wenjiong， TONG Liyong， LIU Shutian. Concurrent Topology Design of Structure and Material Using a Two-scale Topology Optimization［J］. Computers and Structures， 2017， 178：119-128.

［10］ LIU Xinyu， ZOU Anquan. A Human-factors Engineering Based Design Research for E-commerce Express Logistics Sorting System［J］. International Journal of RF—Technologies Research and Applications， 2018，9（1/2）：51-61.

［11］ 楊伟国. 基于全向轮的可编程输送平台的设计与研究［D］. 淮南：安徽理工大学， 2020.

YANG Weiguo. Design and Research of Programmable Delivery Platform Based on Omnidirectional Wheel［D］. Huainan：Anhui University of Science & Technology， 2020.

［12］ CLAUDIO U， ABISH A， HENDRIK T， et al. Control Strategies for Small-scaled Conveyor Modules Enabling Highly Flexible Material Flow Systems［J］. Procedia CIRP， 2019， 79：433-438.

［13］ 高振清， 李明刚， 杜艳平， 等.带双目视觉的全向移动物流机器人设计与实现［J］. 机械科学与技术， 2019， 38（5）：779-782.

GAO Zhenqing， LI Minggang， DU Yanping， et al. Design and Implementation of Omnidirectional Mobile Logistics Robot with Binocular Vision［J］. Mechanical Science and Technology for Aerospace Engineering， 2019， 38（5）：779-782.

［14］ ZAHER W， YOUSSEF A W， SHIHATA L A， et al. Omnidirectional-wheel Conveyor Path Planning and Sorting Using Reinforcement Learning Algorithms［J］. IEEE Access， 2022， 10：27945-27959.

［15］ LUO Qiang， WANG Haibao， ZHENG Yan， et al. Research on Path Planning of Mobile Robot Based on Improved Ant Colony Algorithm［J］. Neural Computing and Applications， 2020， 32（6）：1555-1566.

［16］ 李颀， 汪伟. 多全向轮协同分拣平台的路径规划［J］. 系统仿真学报， 2021，33（3）：698-709.

LI Qi， WANG Wei. Path Designing of Multi-omnidirectional Wheel Collaborative Sorting Platform［J］. Journal of System Simulation， 2021， 33（3）：698-709.

［17］ 杨莹， 张莉， 郭瑞鸿， 等. 基于改进快速搜索随机树算法的包裹分拣路径规划算法［J］.计算机集成制造系统， 2022， 28（3）：951-958.

YANG Ying， ZHANG Li， GUO Ruihong， et al. Improved RRT Based Sorting Path Planning Algorithm for Parcel［J］. Computer Integrated Manufacturing Systems， 2022， 28（3）：951-958.

［18］ 简傲， 闵华松， 黄文晖. 三轮全向移动机器人里程计在线校正方法研究［J］. 机床与液压， 2022，50（3）：1-9.

JIAN Ao， MIN Huasong， HUANG Wenhui. Research on Online Calibration Method of Odometer for Three-wheeled Omnidirectional Mobile Robot［J］. Machine Tool & Hydraulics， 2022， 50（3）：1-9.

［19］ DI C D， EBRAHIMNEJAD A， ALEZAAMIRI H， et al. A Novel Ant Colony Algorithm for Solving Shortest Path Problems with Fuzzy Arc Weights［J］. Alexandria Engineering Journal， 2022， 61（5）：3403-3415.

［20］ SANGEETHA V， RAVICHANDRAN K S， SHEKHAR S， et al. An Intelligent Gain-based Ant Colony Optimisation Method for Path Planning of Unmanned Ground Vehicles［J］. Defence Science Journal， 2019， 69（2）：167-172.

［21］ YANG Wenlin， WU Peng， ZHOU Xiaoqi， et al. Improved Artificial Potential Field and Dynamic Window Method for Amphibious Robot Fish Path Planning［J］. Applied Sciences， 2021， 11（5）：2114-2128.

［22］ 王洪斌， 郝策， 张平， 等. 基于A*算法和人工势场法的移动机器人路径规划［J］. 中国機械工程， 2019， 30（20）：2489-2496.

WANG Hongbin， HAO Ce， ZHANG Ping， et al. Path Planning of Mobile Robots Based on A* Algorithm and Artificial Potential Field Algorithm［J］. China Mechanical Engineering， 2019， 30（20）：2489-2496.