基于摩擦补偿的两轴直驱伺服进给系统自适应非线性滑模轮廓控制
2023-12-01金鸿雁王磊赵希梅
金鸿雁 王磊 赵希梅
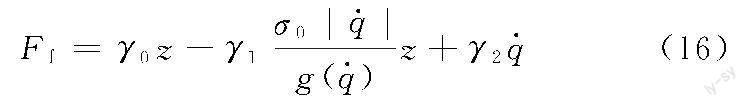
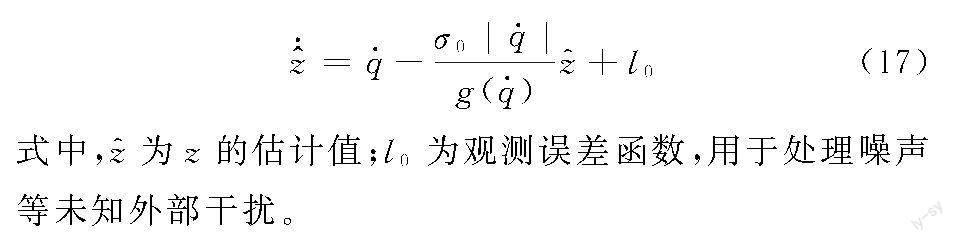
摘要:为满足两轴直驱伺服进给系统的高精度加工要求,提出一种基于摩擦补偿的自适应非线性滑模轮廓控制(ANSMCC)方法,以兼顾加工精度和响应速度要求。建立适用于大曲率轮廓加工的等效轮廓误差模型,同时考虑系统中存在的不确定性动态的影响,建立准确且能实时补偿的改进LuGre非线性摩擦力动力学模型。为提升两轴直驱伺服进给系统轮廓性能,设计基于非线性滑模面的ANSMCC方法,其中非线性滑模面包含轮廓误差分量,通过改变非线性滑模面中增益矩阵值的大小可实时改变系统的阻尼比,从而协调轮廓误差与系统响应速度的关系。实验结果表明,所提方法可以克服系统运行过程中不确定性动态的影响,准确跟踪大曲率轮廓曲线,提高轮廓加工精度。
关键词:两轴直驱伺服进给系统;摩擦补偿;非线性滑模面;轮廓误差
中图分类号:TM351
DOI:10.3969/j.issn.1004132X.2023.11.009
Adaptive Nonlinear Sliding Mode Contour Control of Two-axis Direct Drive
Servo Feed Systems Based on Friction Compensation
JIN Hongyan WANG Lei ZHAO Ximei
School of Electrical Engineering,Shenyang University of Technology,Shenyang,110870
Abstract: In order to meet the requirements of high precision for two-axis direct drive servo feed systems, based on friction compensation, an adaptive nonlinear sliding mode contour control(ANSMCC) method was proposed to take into account the requirements of machining precision and response speed. An equivalent contour error model suitable for large curvature contour machining was established, and considering the influences of uncertain dynamics in the system, an improved LuGre nonlinear friction dynamic model with accurate and real-time compensation was established. In order to improve the contour performance of the two-axis direct drive servo feed systems, an ANSMCC method was designed based on the nonlinear sliding mode surface, where the nonlinear sliding mode surface contained the contour error components. By changing the values of the gain matrix in the nonlinear sliding mode surface, the damping ratio of the system might be changed in real time, so as to coordinate the relationship between the contour errors and the system response speeds. The experimental results show that the proposed method may overcome the dynamic influences of uncertainty in the operation of system, accurately track the large curvature contour curves, improve the contour machining accuracy.
Key words: two-axis direct drive servo feed system; friction compensation; nonlinear sliding mode surface; contour error
0 引言
两轴直驱伺服进给系统是高档数控装备中实现高精密平面运动的主要功能部件,它由两台直线电机驱动,具有快响应、高可靠性和高精度的优点[1]。然而,双轴之间存在的运动协调问题以及运行过程中受到的负载变化、摩擦力等不确定性问题使两轴直驱进给系统的轮廓精度受到极大影响,尤其是当期望轮廓为大曲率复杂轨迹时,轮廓误差会显著增大[2],为此,需要建立精确计算轮廓误差的模型并设计合适的轮廓控制器。
为提高轮廓加工精度,国内外专家学者采用设计前馈或反馈控制器的方式来提高单轴跟踪精度,进而提高轮廓运动控制精度。文献[3]和文献[4]分别将交叉耦合互补滑模控制和二阶离散分数阶滑模控制方法应用到直驱伺服系统中,克服了系统中不确定性因素的影响,提高了单轴位置跟踪精度,减小了轮廓误差。然而,这种纯运动的控制方法忽略了各轴间的协调配合作用,在一些应用场合下无法保证良好的轮廓跟踪效果[5]。为此,一些学者通常采用局部任务坐标系轮廓运动控制方法和交叉耦合控制方法等能够增强轴间运动协调性能的轮廓控制方案。文献[6]设计了基于全局任务坐标系的互补滑模轮廓控制方法,有效提高了直驱XY平台的轮廓跟踪精度。文献[7]将基于速度前瞻的交叉耦合轮廓控制应用到双轴直线电机中,显著减小了轮廓误差。然而,此类控制器在设计时将每个进给驱动轴的跟踪和轮廓均作为控制器的输入,致使参数繁多调节困难,且选取不适当的参数会造成轮廓跟踪性能的下降。文献[8]在系统动力学模型的基础上,直接设计基于超螺旋滑模控制的等效误差轮廓控制器用于直线电机精密运动平台的轨迹跟踪,能够有效地抑制不确定性扰动,提高轮廓加工精度。文献[9-10]将空间迭代学习轮廓控制方法应用于直线电机进给系统中,能够精确跟踪大曲率、复杂曲线,确保轮廓加工精度。此类非轮廓控制器基于轮廓误差模型,在设计非轮廓控制器时将单轴电机的误差信息作为输入量,可同时兼顾單轴轨迹跟踪和多轴运动协调控制[11]。
为提高两轴直驱伺服进给系统的轮廓加工性能,本文设计了基于摩擦补偿的两轴直驱进给系统自适应非线性滑模轮廓控制(adaptive nonlinear sliding mode contour control,ANSMCC)方法。首先,通过坐标变换的方式建立等效轮廓误差模型与含有非线性摩擦力补偿的系统动力学模型。然后,基于系统模型设计ANSMCC方法,利用轮廓误差分量设计非线性滑模面,通过调整增益矩阵值,可以改变系统阻尼比,利用高阻尼比减小超调量,利用低阻尼比提高系统响应速度,从而平衡轮廓跟踪误差与响应速度之间的关系。通过实验验证了该方法可以保证两轴直驱伺服进给系统在复杂轮廓下的跟踪精度,实现高性能数控装备的精密轮廓加工要求。
1 两轴直驱伺服进给系统模型
1.1 等效轮廓误差模型
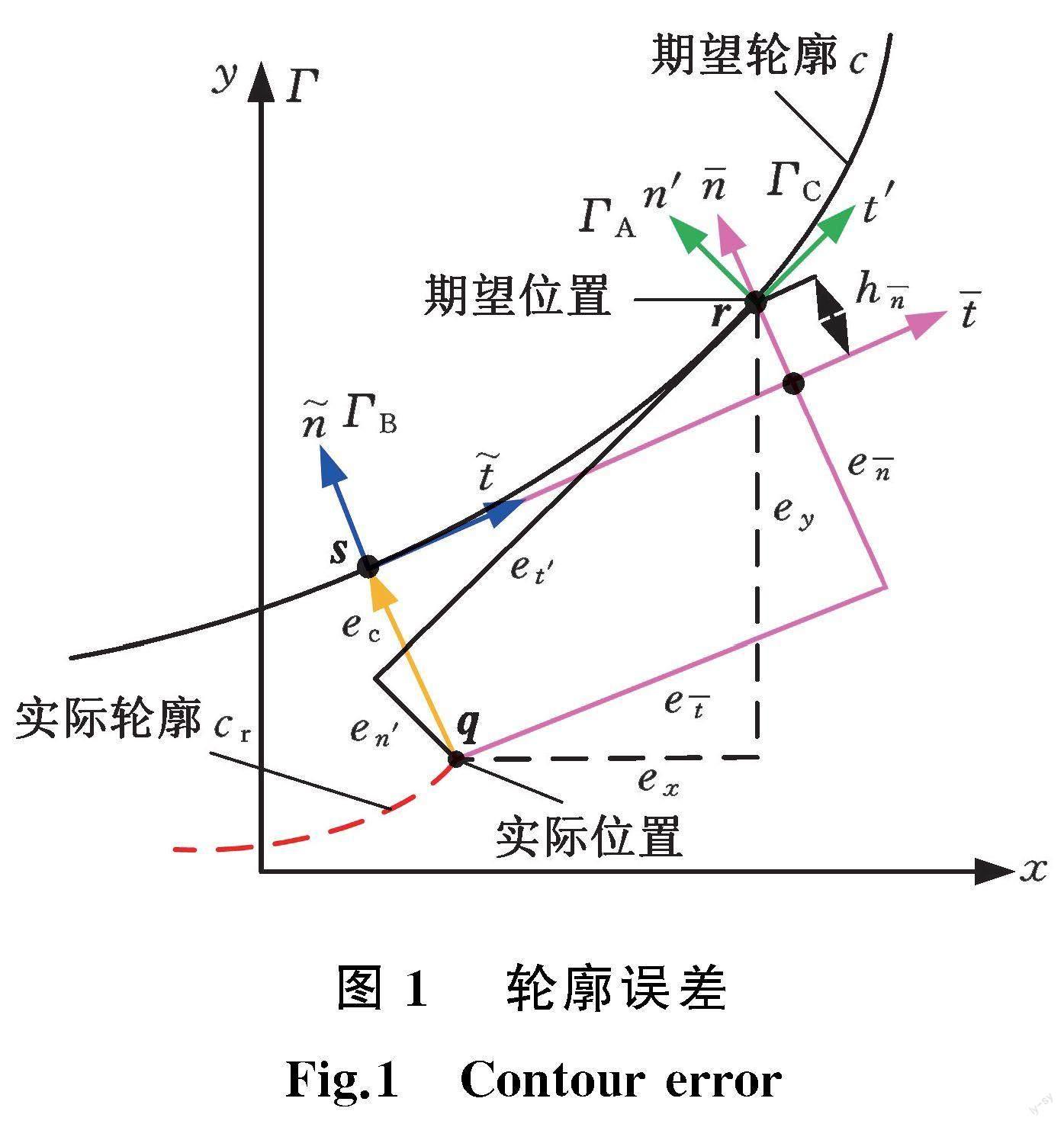
轮廓误差是指实际加工位置到参考位置的最短距离,是评估双轴直驱伺服进给系统加工精度的关键性指标,主要受到单轴跟踪误差和多轴联动协调性的影响[12]。对于每个进给驱动轴,轮廓误差与单轴位置跟踪误差之间的关系如图1所示。
Γ为固定坐标系,其横纵轴分别为x和y,代表两个进给驱动轴上的x电机和y电机。在此坐标系下,c为期望轮廓;cr为实际轮廓;ec为轮廓误差,与加工零件的形状直接相关;期望位置为r=(rx,ry)T;实际位置为q=(qx,qy)T。各轴的跟踪误差e定义为
e=q-r=(ex,ey)T(1)
式中,e为跟踪误差向量;ex为x轴电机的位置跟踪误差;ey为y轴电机的位置跟踪误差。
在机械加工中,轮廓误差直接关系到被加工零件的形状。然而,当期望轮廓c较为复杂时,很难直接获得实时轮廓误差值。为获得轮廓误差ec的近似值,通常可以采用等效轮廓误差方法。在期望位置r处,建立坐标系ΓA,其轴t′在c处与r相切,轴n′与轴t′相互垂直,则在此坐标系下的方向向量为
式中,t′x、t′y分别为x轴电机和y轴电机在坐标系ΓA下t′坐标轴方向上的位置分量;n′x、n′y分別为x轴电机和y轴电机在坐标系ΓA下n′坐标轴方向上的位置分量。
根据式(2)、式(3),并结合式(1),可得在ΓA坐标系下的位置跟踪误差eA为
式中,et′、en′分别为与期望轮廓曲线c上位置r处相切和垂直的误差分量;Λ为由位置分量构成的矩阵。
通常,可将式(4)中的误差分量en′视为实际轮廓误差的近似值。然而,当期望轨迹的曲率较大时,这种近似方法不是很准确。为避免该问题,假设期望位置r和期望轨迹上的点s之间的距离近似等于切向误差et′,且沿该段的期望速度几乎恒定,则r到s这段距离之间的速度等于r处的期望速度,因此,从s运动到r所需时间表示为
根据式(6)、式(7),结合式(1),可得在ΓB坐标系下的跟踪误差为
1.2 两轴直驱伺服进给系统非线性动力学
两轴直驱伺服进给系统由两台永磁直线同步电机相互垂直安装构成,下层为x轴电机,上层为y轴电机,具体包含工作台、直线导轨、光栅检测装置等部件。两轴直驱伺服进给系统动力学模型可表示为
式中, mx、my分别为x轴电机和y轴电机的动子质量; Dx、Dy分别为x轴电机和y轴电机所受的扰动量,包含参数变化、负载扰动等;Ffx、Ffy分别为x轴电机和y轴电机所受的非线性摩擦力; Fex、Fey分别为x轴电机和y轴电机的电磁推力; Kex、Key分别为x轴电机和y轴电机的电磁推力系数;iqx、iqy分别为x轴电机和y轴电机的q轴电流。
对于两轴直驱伺服进给系统,摩擦力是该系统运行过程中不容忽视的非线性扰动,对系统的运行精度有较大影响。然而传统的摩擦模型不能很好地描述平台摩擦力在低速区、高速区的非线性特性。为此,本文单独考虑非线性摩擦力对系统的影响并进行补偿,以x轴电机所受摩擦力为例建立摩擦模型,y轴电机模型与下述设计相同。为简化公式,省去x轴电机变量的下角标x,设计补偿模型如下。
传统的LuGre摩擦力模型是应用最为广泛的描述摩擦动态行为的模型,可表示为[13]
其中,z为不可测的摩擦状态; σ0为标称静摩擦参数,σ0>0;γ0、γ1、γ分别为刚度系数、阻尼系数和黏滞摩擦系数;g(q·)>0用于描述Stribeck效应,可表示为
式中,Fc、Fs分别为库仑摩擦力和静摩擦力;vs为Stribeck速度。
将式(14)代入到式(13)中,可得
其中,γ2=γ1+γ。
z为不可测内状态,需要采用状态观测器来观测,设计为
在实际应用中,式(16)中的LuGre模型参数γ0、γ1、γ通常设置为常数,然而,由于机械磨损和运行环境的变化,这三个参数可能会随着电机的位置而发生变化,若将三个参数设置为常数则不能准确地描述摩擦力的非线性动力学。
为此,提出改进的自适应LuGre摩擦模型,采用NURBS样条函数表示直线伺服电机的位置,改进的模型参数γ0、γ1、γ分别表示为
其中,γ0l、γ1l、γ2l分别为第l个拟合基准点下的刚度系数、阻尼系数和黏滞摩擦系数;l(l=1,2,…,m)为拟合基准点数,m为基准点总数;k为NURBS样条的阶数,取为k=3; Sl,k(q)为k阶样条函数,可表示为
其中,(T1,T2,…,Tm+k-1,Tm+k)为一组节点向量,满足Tl+1≥Tl。
将式(18)~式(21)代入到式(16)中,即可得到改进的LuGre摩擦力模型。取m=3为电机极对数,则Tk为第一对磁极位置,Tk+m为最后一对磁极位置。因此,采用NURBS样条函数表示的LuGre摩擦模型可以表征摩擦力随每对磁极的函数变化,能更准确地描述电机速度位置变化等因素引起的摩擦力改变,从而对摩擦力进行有效补偿,并减小轮廓误差。
2 两轴直驱伺服进给系统的ANSMCC设计
在传统的滑模控制设计中,通常采用线性滑模面,无论误差大小,系统的阻尼比都保持不变。在控制系统中,最重要的要求是快速响应和小超调。然而,快速响应会产生较大的超调,从而增大轮廓误差,反之,小超调则影响系统的响应速度,因此,采用线性滑模面很难同时实现快速响应与小超调量。为此,在ANSMCC中,设计非线性滑模面来权衡两者之间的矛盾,非线性滑模面可表示为
其中,S∈R2×1为非线性滑模面,由线性项和非线性项组成;Q∈R2×2为滑模面的线性增益矩阵,该矩阵的选择应确保闭环系统中主导极点具有较小的阻尼比,这是由于主导极点所对应的响应分量在系统响应中起主导作用,且Q需满足李雅普诺夫方程PQT+QP=W;W为正定矩阵;P∈R2×2为对称正定矩阵,用于调整最终阻尼比;I为单位矩阵;ζ∈R2×2为S中的非线性项,用于改变系统的阻尼比,ζ选择为[14]
通过分析可得出,在非线性滑模面中,线性项Q包含一个阻尼比非常小的增益矩阵,用于促进系统的快速响应。非线性项ζ用于提供可变的系统阻尼比,以平衡閉环系统的快响应和小超调量。通过应用非线性滑模面,可使闭环系统的阻尼比从其初始低值变化为最终高值,阻尼比的初始低值用于提高快速响应,随后的高阻尼比用于减小超调。
在滑模控制中,控制律的设计是十分重要的,可以迫使系统状态点运动到滑模面S上,并满足理想滑模面S=0,因此,由式(22)可得
为证明控制器设计的稳定性,选取李雅普诺夫函数为
V=eTcPec(26)
根据式(25),并对式(26)求导可得
根据式(1)及式(11),在固定坐标系Γ下可得
根据式(9)、式(10)和式(28),可得
根据式(22)设计的非线性滑模面,假设期望速度和加速度已知,将式(28)代入式(29)中,并结合式(11)和式(12),可得
其中,u=iq为ANSMCC的控制输入;Z∈R2×2为对角增益矩阵;G∈R2×2为对角矩阵,其对角线元素Gx和Gy是通过x轴电机和y轴电机所受的扰动量Dx、Dy的上界值选择的,表示为
式中,max(Dx)、max(Dy)为D中元素的最大值。
为解决滑模控制的抖振问题,采用饱和函数sat(S)替换式(30)中的sgn(S)[14],设计为
式中,δj为边界层厚度值。
此外,在式(30)设计的控制律中,控制增益Z用于改善系统的动、静态性能。然而,由于Z是恒定的,不能随着系统轮廓误差值的改变而实现实时变化,因此,为提高系统轮廓性能,设计自适应律使Z可以根据系统轮廓误差值的大小而自动实时调整,自适应律设计为
其中,ρ为正常数;Sm为与滑模面对角线元素相关的对角矩阵。由式(33)可以看出,控制增益Z的值与滑模面有关,而滑模面(式(22))的设计又包含系统的轮廓误差ec,因此,Z(t)可以随着轮廓误差值的变化而实现在线实时调整,从而提高轮廓精度。
因此,结合式(32),将式(33)应用到式(30)中,可得ANSMCC的控制律为
3 系统实验分析
两轴直驱伺服进给系统实验装置如图2所示。该实验系统主要包括上位机、运动控制实验箱、两轴直驱运动平台和直线光栅检测装置等部件。图中,直线光栅编码器为美国GSI公司生产的Micro-E型号,分辨力为0.1 μm。实验装置通过RS232通信口将上位机与两台直线电机的驱动器相连。利用MATLAB/Simulink界面将仿真模型编译为C代码,下载到实验箱控制两轴直驱伺服进给系统按照输入指令运行。最后,将实验结果以txt、xls等格式传输到MATLAB软件中,从而利用强大的MATLAB数据处理功能进行数据分析。实验中采用的两轴直驱运动平台的有效行程为分别为:220 mm(x轴)、260 mm(y轴),
其主要参数为:mx=2 kg、my=2 kg、Kex=24 N/A、Key=35 N/A。
为验证ANSMCC对实现高精度轮廓跟踪的可行性和有效性,实验分别在空载标称条件和负载参数变化两组条件下进行,采用如下四种方法:
(1)C1方法。采用线性滑模面的传统滑模轮廓控制(sliding mode contour control,SMCC)方法,选取ζ=0为线性滑模面,Q=diag(10,20)为相对小阻尼比。
(2)C2方法。采用线性滑模面的SMCC方法,选取ζ=0为线性滑模面,Q=diag(25,50)为相对大阻尼比。将C2与C1对比,以验证阻尼比大小对系统轮廓性能的影响。
(3)C3方法。采用非线性滑模轮廓控制(nonlinear sliding mode contour control,NSMCC)方法,选取ζ≠0为非线性滑模面。将C3与C1、C2相比,以验证非线性滑模面对系统轮廓跟踪能力的影响。
(4)C4方法。采用ANSMCC方法,选取ζ≠0为非线性滑模面。将C4与C2和C3进行对比,以验证采用自适应律估计控制增益对轮廓精度提高的有效性。
为保证对比实验的公平性,四种控制器中初始条件相同,参数如表1所示。
为评估轮廓控制器的控制性能,定义如下性能指标:
式中,VRMS为轮廓误差的均方根值(RMS值);T为总运行时间;VMAX为轮廓误差的最大值(MAX值);VURMS为控制输入u的均方根(URMS值),用于衡量控制输入的大小。
首先,为测试所提出ANSMCC方法的轮廓运动性能,命令两轴直驱运动平台跟踪星形期望轮廓,平台在标称状态下空载运行。C1、C2、C3和C4四种方法控制下的系统星形轮廓跟踪曲线见图3,可以看出,四种方法均可以较好地跟踪期望轮廓轨迹。为清晰对比,给出了四种方法控制下的两轴直驱运动平台的轮廓误差曲线,见图4。此外,以x轴电机为例,在四种方法控制下的控制输入曲线见图5。表2为两轴直驱运动平台在跟踪星形轮廓实验中的性能情况表。
观察图3~图5以及表2,对比C1、C2和C3的轮廓误差曲线和控制输入曲线能够发现,尽管C2中阻尼比的增大能够提高系统的轮廓跟踪精度,使其与C3所得的轮廓性能相近,但控制输入曲线图5c和图5d相比于图5a和图5b更为平滑,曲线的波动幅度明显变小,这是由于非线性滑模面包含轮廓误差分量,能够实时改变系统的阻尼比,从而减小轮廓误差,使控制输入更加平稳。此外,对比图4c和图4d以及表2可以看出,采用自适应律估计参数后,C4控制下的系统轮廓误差显著减小,轮廓误差的RMS值达到1.33 μm,相比于C3,C4控制下的轮廓控制精度提高了37.85%。因此,本文提出的ANSMCC方法在轮廓跟踪能力方面具有优越性。
为测试所提ANSMCC方法克服扰动的能力,对系统给定花瓣期望轮廓轨迹,拖动2 kg负载在参数变化条件下运行(实际黏滞摩擦系数为标称值的1.5倍)。采用四种方法跟踪花瓣轮廓的跟踪曲线见图6。图7和图8分别为轮廓跟踪误差曲线和控制输入曲线。花瓣轮廓跟踪实验性能指标如表3所示。通过表3可以看出,在引入非线性滑模面和自适应律后,轮廓誤差的RMS值减小到1.46 μm,相比于C1、C2和C3的RMS值,分别减小了64.82%、56.55%和47.48%;轮廓误差的MAX值减小到1.96 μm,相比于C1、C2和C3的MAX值,分别减小了66.61%、53.44%和51.60%。由此可得,本文提出的ANSMCC方法能有效提高两轴直驱伺服进给系统的轮廓跟踪精度。
4 结论
为实现两轴直驱伺服进给系统在实际加工过程中的高精度运行,提出基于摩擦补偿的自适应非线性滑模轮廓控制(ANSMCC)策略。在建立等效轮廓误差模型和非线性动力学模型的基础上,提出了基于非线性滑模面的ANSMCC方法。最后通过实验得出:
(1)通过引入非线性滑模面和自适应律,ANSMCC方法能够有效提高两轴直驱伺服进给系统的轮廓跟踪精度。
(2)本文提出的轮廓控制策略简单可行,能够有效克服参数变化、负载扰动等对轮廓性能的影响,提高系统对不确定性的鲁棒性。
参考文献:
[1] 刘艳雄,王根聚,华林,等.采用自适应滑模变结构控制的精冲机双驱动协调控制系统[J]. 中国机械工程,2021,32(18):2189-2196.
LIU Yangxiong,WANG Genju,HUA Lin,et al.Double-drive Coordinated Control Systems of Fine Stamping Machines Based on Adaptive Sliding Mode Variable Structure Control[J].China Mechanical Engineering,2021,32(18):2189-2196.
[2] 李超.冗余直驱龙门系统的多输入多输出精密运动控制[D].杭州:浙江大学,2018.
LI Chao. MIMO Precision Motion Control of Redundantly Driven Gantry Systems with Direct Actuators[D].Hangzhou:Zhejiang University,2018.
[3] 赵希梅,赵久威.精密直驱龙门系统的交叉耦合互补滑模控制[J].电工技术学报,2015,35(11):7-12.
ZHAO Ximei,ZHAO Jiuwei. Cross-coupled Complementary Sliding Mode Control for Precision Direct-drive Gantry System[J]. Transactions of China Electrotechnical Society,2015,35(11):7-12.
[4] KUANG Z A,GAO H J,TOMIZUKA M. Precise Linear-motor Synchronization Control via Cross-coupled Second-order Discrete-time Fractional-order Sliding Mode[J].IEEE/ASME Transactions on Mechatronics,2019,14(2):1-11.
[5] LIU Yang,WAN Min,XIAO Qunbao,et al. Combined Predictive and Feedback Contour Error Control with Dynamic Contour Error Estimation for Industrial Five-axis Machine Tools[J].IEEE Transactions on Industrial Electronics, 2022,69(7):6668-6677.
[6] 原浩,赵希梅.基于全局任务坐标系的直驱XY平台学习互补滑模轮廓控制[J].电工技术学报,2020,35(10):2141-2148.
YUAN Hao,ZHAO Ximei.Learning Complementary Sliding Mode Contouring Control Based on Global Task Coordinate Frame for Direct Drive XY Table[J].Transaction of China Electrotechnical Society,2020,35(10):2141-2148.
[7] 曾子强,曹荣敏,侯忠生,等.二维直线电机的多入多出无模型自适应轮廓控制[J].控制理论与应用,2020,37(5):1007-1017.
ZENG Ziqiang,CAO Rongmin,HOU Zhongsheng,et al. Multiple Input Multiple Output Model Free Adaptive Contour Control for Two-dimensional Linear Motor[J].Control Theory & Applications,2020,37(5):1007-1017.
[8] 武志涛,朱连成.基于滑模轮廓控制器的直线电机精密运动平台轨迹跟踪控制[J].中国电机工程学报,2015,35(23):6188-6193.
WU Zhitao,ZHU Liancheng.Trajectory Tracking Control for the Motion Table Driven by Linear Motors Based on Sliding Mode Contour Tracking Controllers[J].Proceedings of the CSEE,2015,35(23):6188-6193.
[9] LI Jiangang,WANG Yiming,LI Yanan,et al. Reference Trajectory Modification Based on Spatial Iterative Learning for Contour Control of Two-axis NC Systems[J].IEEE/ASME Transactions on Mechatronics,2020,25(3):1266-1275.
[10] HENDRAWAN Y M,FARRAGE A,UCHIYAMA N. Iterative NC Program Modification and Energy Saving for a CNC Machine Tool Feed Drive System with Linear Motors[J].The International Journal of Advanced Manufacturing Technology,2019,102(3):3543-3562.
[11] YANG Ming,YANG Jixiang,ZHU Limin,et al.A Novel Curvature Circle Iterative Algorithm for Contour Error Control of Multi-axis CNC Machine Tools[J].Precision Engineering,2020,65:23-31.
[12] 謝东,丁杰雄,霍彦波,等. 数控机床转动轴进给系统轮廓误差分析[J].中国机械工程,2012,23(12):1387-1392.
XIE Dong,DING Jiexiong,HUO Yanbo,et al.Contour Error Analysis for Rotation Feed Axis in CNC Machine[J].China Mechanical Engineering,2012,23(12):1387-1392.
[13] 韦为,耿葵花,耿爱农,等.基于LuGre模型的转子压缩机滑片滑槽运动副摩擦力测试[J].中国机械工程,2019,30(8):932-938.
WEI Wei,GENG Kuihua,GENG Ainong,et al.Frictional Force Test of Rotor Compressor Slides-chute Movement Deputy Based on LuGre Model[J].China Mechanical Engineering,2019,30(8):932-938.
[14] JIN Hongyan, ZHAO Ximei, WANG Tianhe. Adaptive Backstepping Complementary Sliding Mode Control with Parameter Estimation and Dead-zone Modification for PMLSM Servo System[J]. IET Power Electronics, 2021, 14(4):785-796.
