线性液动压抛光加工的流场特性研究
2023-12-01傅远韬文东辉孔凡志淦作昆成志超
傅远韬 文东辉 孔凡志 淦作昆 成志超

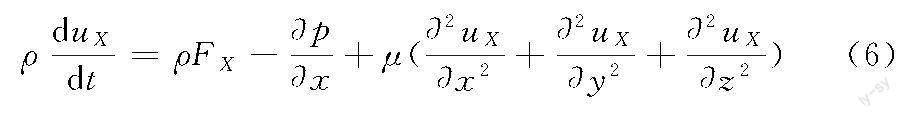

摘要:分析了线性液动压抛光加工中液流对工件表面的作用形式,推导了黏性切应力和液动压力数学模型。对线性液动压抛光流场进行了数值模拟,剖析了抛光辊子尺寸以及抛光工艺参数对液动压和黏性切应力的数值及分布均匀性的影响规律。研究结果表明:液动压力和黏性切应力数值随辊子直径和辊子转速的增加而增加,与此同时其分布均匀性反而下降;抛光间隙值越小,液动压力和黏性切应力数值越大,且其分布均匀性越好。最后采用自制的线性液动压抛光实验平台,以K9玻璃为实验对象,探究了抛光加工表面形貌和表面粗糙度的创成过程。
关键词:线性液动压抛光;液动压力;黏性切应力;流场;表面形貌;表面粗糙度
中图分类号:TG580
DOI:10.3969/j.issn.1004132X.2023.11.006
Research on Characteristics of Flow Fields during LHP Processes
FU Yuantao1,2 WEN Donghui1,2 KONG Fanzhi1,2 GAN Zuokun1,2 CHENG Zhichao1,2
1.Special Equipment Manufacturing and Advanced Processing Technology, Ministry of Education/
Zhejiang Provincial Key Laboratory,Hangzhou,310023
2.School of Mechanical Engineering,Zhejiang University of Technology,Hangzhou,310023
Abstract: The action form of fluid flow on workpiece surfaces in LHP was analyzed, the mathematic models of viscous shear stress and hydrodynamic pressure were derived. The flow field of LHP was numerically simulated and the influences of the sizes of polishing roller and polishing parameters on the numerical values and distribution uniformities of hydrodynamic pressure and viscous shear stress were analyzed. The results show that the values of hydrodynamic pressure and viscous shear stress increase with the increasing of roller diameters and rotation speeds, while the distribution uniformity decreases. The smaller the values of polishing clearance, the larger the values of hydrodynamic pressure and viscous shear stress, and the better the distribution uniformity. Finally, taking K9 glass as the experimental object, the formation processes of surface morphology and surface roughness were investigated by using a self-made LHP experimental platform.
Key words: linear hydrodynamic polishing(LHP); hydrodynamic pressure; viscous shear stress; flow field; surface topography; surface roughness
0 引言
依賴于磨粒与工件表面软性接触的流体动压抛光技术是获取少无损伤、超光滑表面的主流方法之一,由于改善了磨粒与工件表面的刚性接触状态,可以获得较高的表面精度、少无表面损伤,又因为抛光工具磨损趋势缓慢,因此抛光过程的稳定性和可重复性好,有望实现低损伤超光滑的加工效果[1-2]。
MORI等[3-4]提出并研究了弹性发射加工(elastic emission machining,EEM),加工过程中聚氨酯球高速旋转,使抛光间隙内形成液动压力并驱使抛光液中的磨粒对工件表面产生冲击,在单晶硅、碳化硅和K9玻璃材料上均实现了原子级超光滑表面加工。SU等[5]研究了不同润滑条件下EEM的材料去除速率变化规律,研究结果表明该方法的加工速率与润滑膜的剪切应力存在正相关性。NAMBA等[6]提出浮法抛光,采用高平面度、微沟槽的锡盘,工件与抛光盘之间形成的动压液膜效应可超过材料断裂韧性的阈值,从而产生材料去除并保持磨粒与工件表面呈现软性接触状态。WATANABE等[7]提出了动压浮离抛光,利用抛光盘转动时抛光液流经楔形结构流道产生液动压,使工件产生动压浮离效应,抛光粒子在浮离空隙中对工件进行抛光加工。对于以圆盘形为抛光工具的浴法抛光、浮法抛光、动压浮离抛光和盘式流体动压抛光,其流场特征是沿抛光盘直径朝圆心方向上,流体的速度场、压力场呈现梯度增大,因此导致抛光区域的液体动压力和材料去除速率分布不均。
PENG等[8]提出了液动压效应抛光,该方法利用化学冲击反应实现材料的弹性区域内去除加工,可以有效去除材料表面和亚表面损伤。WEN等[9]提出了液动压悬浮抛光,在动压浮离抛光结构基础上添加了约束边界和蓄流槽从而形成新型抛光工具盘,使得工件能够在液动压和流体剪切力稳定区域实现抛光加工。郑子军等[10]对液动压悬浮抛光工具盘结构参数进行了优化,优化后抛光工具盘产生的动压力均值和均匀性都提高了30%。CAO等[11]在弹性发射加工和流体射流抛光的基础上提出了新型圆盘流体动力抛光,液膜作为磨粒的载体存在于抛光工具与抛光表面之间,还发现可以通过增加额外去除量的方式减小单一波长的面形误差。付有志等[12]提出了集群磁流变动压复合抛光方法,通过动态周期性挤压磁流变液抛光垫,增大抛光压力并增加有效磨粒数,实现了集群磁流变液磨粒的多维运动,强化了抛光力学特性,提高了抛光效率和质量。采用中心供液方式有效改善了局部压力分布的均匀性,但总体特征没有发生变化,因此对材料的均匀去除和表面粗糙度、轮廓参数及表面微观形貌的调控能力尚有进一步提升空间。
线性液动压抛光(linear hydrodynamic poli-shing,LHP) 方法采用了圆柱抛光辊子,所形成的液动压力与黏性切应力呈线状分布且均匀,合理控制工件的进给速率有望实现高转速的均匀抛光加工。本文分析了线性液动压抛光加工的基本原理,建立了黏性切应力和液动压力的数学模型,数值模拟了抛光辊子尺寸及抛光工艺参数对黏性切应力和液动压力的作用规律,研究了黏性切应力和液动压力的数值大小及其分布均匀性,并采用自制的线性液动压抛光实验平台,以K9玻璃为实验对象,探究了平面抛光加工表面形貌和表面粗糙度的创成过程,为后期获得更好的表面形貌和粗糙度提供了一定的參考价值。
1 线性液动压抛光加工
1.1 线性液动压抛光原理
线性液动压抛光原理如图1所示,工件完全浸没于含有纳米粒子的黏性抛光液中,表面圆柱形抛光辊子高速回转,同时工件与抛光辊子保持着微米级间隙并做往复平移。线性液动压抛光加工过程中,抛光辊子与工件表面构成的楔形间隙区域会产生流体动压润滑效应[13],同时磨粒在抛光辊子高速回转所产生的高流速作用下以较高的速度对工件表面粗糙峰进行冲刷,从而实现原子级材料去除加工。
1.2 材料表面微粗糙峰的受力分析
1.2.1 线性液动压流场的抛光力
抛光过程中工件表面的受力可以分别表现为:在Y方向的液动压力p和在X方向的黏性切应力τ,如图2所示。由动压效应产生的液动压力p驱动抛光液中的磨粒对工件表面的粗糙峰进行冲击、碰撞,促进材料的松弛并减小键结合力。由高速旋转的抛光辊子带动的抛光液产生较大的流体速度梯度,再由黏性效应产生较大的黏性切应力τ,该作用力对工件表面的粗糙峰进行冲击、滑擦以抵抗材料的键结合力,从而实现材料的去除。
在实际抛光加工过程中,作用力p和τ将共同驱使微细磨粒对工件表面粗糙峰进行冲击、碰撞、滑擦,从而实现材料的去除。
1.2.2 抛光力模型
1.2.2.1 液动压力
Reynolds方程[14]作为流体动压润滑理论的基本方程,阐明了在黏性流体环境中的一般形式可根据质量守恒方程和动量守恒方程并满足以下基本假设推导得出:
①忽略流体体积力作用的影响;
②固体界面与相邻流体界面的速度相同;
③液膜厚度方向动压大小保持不变。
基于上述假设,推导得出Reynolds方程的一般形式如下:
式中,ρ为流体密度;h为动压液膜厚度;μ为流体动力黏度;u1、u2分别为动压液膜上下表面的X向速度;v1、v2分别为液膜上下表面的Z向速度;w1、w2分别为液膜上下表面的Y向速度;x、z分别为X向和Z向的位移。
线性液动压抛光加工过程中,抛光液可视为不可压缩流体,流体密度ρ为定值,即变密度效应可忽略不计;辊子以Z轴为中心高速旋转,圆柱辊子转速为定值,则此时液膜上下表面沿X轴方向的速度u1、u2可视为定值;忽略圆柱辊子的制造精度和安装精度以及仪器振动的影响,则圆柱辊子沿Z轴方向的速度v1+v2=0,因此可忽略伸缩效应;同时流体在Y轴方向的速度也可视为0,即可忽略挤压效应。由此Reynolds方程可简化为
1.2.2.2 流体黏性切应力
根据广义牛顿内摩擦定律,抛光间隙中的流体黏性切应力定义为
式中,y为Y向的位移;du/dy为Y向的流体速度梯度。
引入流体动量守恒方程(即N-S方程)[15],对于不可压缩黏性流体,它在X向的微分形式为
其中,等号左侧为惯性力作用项;等号右侧依次为体积力、压差力、黏性力;FX为控制体质量力在X向的分量;uX为流体在X向的速度。
忽略惯性力及体积力影响,又因为抛光间隙中的流体只会存在Y向的速度梯度,则式(6)可简化为
对式(7)中y进行两次积分,得到
式中,a、b为常数。
线性液动压抛光加工情形下,当无限趋近于工件表面的流体速度为0即y=0时,uX=0;当无限趋近于抛光辊子表面的流体速度等于辊子线速度即y=h时,uX= u0,其中u0为辊子边缘线速度,h为工件面到辊子面的垂直距离(即动压液膜厚度)。代入上述边界条件并联立式(4),则抛光间隙中任意位置X向的流体速度为
将式(9)代入式(5),得到抛光间隙中的流体黏性切应力表达式为
2 线性液动压流场的数值模拟研究
线性液动压抛光过程中的材料去除作用主要受液动压力p和黏性切应力τ的影响,其中液动压力来自动压效应,流体黏性切应力来自流体的黏性作用。上述两种作用的强弱及分布均匀性将对工件表面微观形貌产生直接影响。
将前处理的流场模型导入FLUENT进行数值模拟,数值模拟条件为:抛光辊子直径40 mm、长度30 mm、辊子转速24 000 r/min、抛光间隙20 μm。选取工件表面为观察面,其液动压力与黏性切应力分布如图3所示。以图3b与图3d中坐标系为参考,分别提取x=0时的Z向数据,绘制液动压力与黏性切应力分布曲线[16-17],见图4。分析图3和图4可知,液动压力和黏性切应力的分布特点是在工件表面X方向上呈中间大、两端小,Z方向上呈倒“U”形的分布形式。图4a与图4b中液动压力与黏性切应力中间区域的变化率分别为1.58%和1.29%,判定为稳定区域,更适合工件表面的均匀加工,两端骤降的分布区域称为骤降区域,不适宜工件表面的均匀加工。
液动压抛光加工過程中,应保持工件处于液动压力与黏性切应力的稳定区域,一方面,根据工件尺寸调整辊子尺寸与工艺参数范围;另一方面,控制好X向的进给速率。通过此方法可以实现液动压力与黏性切应力分布均匀区域内的材料去除加工。
2.1 抛光辊子尺寸的选择
主要研究辊子长度以及辊子直径对抛光流场液动压力和黏性切应力的数值大小及其分布均匀性的影响规律。以前述所选取观察面上Z向数据线的液动压力和黏性切应力的数值大小、分布宽度以及分布均匀性为指标进行对比分析,构建单因素实验表,见表1。
为分析圆柱辊子长度L对液动压力与黏性切应力的影响规律,选取辊子直径为40 mm,辊子转速为24 000 r/min,抛光间隙为20 μm。为探究圆柱辊子直径D对液动压力与黏性切应力的影响,选择辊子长度为30 mm,辊子转速为24 000 r/min,抛光间隙为20 μm。将数值模拟后得到的相应液动压力与黏性切应力数据绘制成分布特性曲线,见图5。
由图5a、图5b可知,抛光辊子长度的改变不会影响液动压力和黏性切应力的大小以及曲线两端液动压力降和黏性切应力降的长度。但当抛光辊子长度为15 mm时,该长度小于两端液动压力降和黏性切应力降的长度,这就会导致辊子长度不足以支撑液动压力与黏性切应力达到在此抛光条件下的最大值。但过长的辊子会放大制造及装配误差,影响材料的均匀去除,因此要保证抛光辊子长度略大于工件长度加上两端液动压力降和黏性切应力降的长度。
由图5c、图5d可知,当辊子直径增大时,曲线两端液动压力降和黏性切应力降的长度也会随之增大,但过大的辊子直径会导致液动压力与速度的分布均匀性变差,显然这对材料的均匀去除会产生不利影响,因此,在保证其去除作用足够的情况下,对于直径越小的抛光辊子,它产生的液动压力与黏性切应力稳定区域越大。
2.2 抛光加工工艺参数的选择
主要研究辊子转速及抛光间隙对抛光流场液动压力及黏性切应力的影响规律。以观察工件面上Z向的液动压力和黏性切应力大小及分布均匀性为指标进行对比分析,构建单因素实验表,见表2。
为探究抛光辊子转速n对液动压力与黏性切应力的影响规律,选择辊子长度为30 mm,辊子直径为30 mm,抛光间隙为20 μm。为探究抛光间隙h0的对液动压与黏性切应力的影响规律,选择辊子长度为30 mm,辊子直径为30 mm,辊子转速为24 000 r/min。将数值模拟后得到的相应液动压力与黏性切应力数据绘制成分布特性曲线,见图6。
由图6a、图6b可得,抛光辊子转速与液动压力和黏性切应力大小成正相关,辊子转速越大,液动压力和黏性切应力就越大。但过高的辊子转速会导致液动压力和黏性切应力的分布均匀性降低,不利于工件表面材料的均匀去除。
由图6c、图6d可得,抛光间隙大小与液动压和黏性切应力大小成负相关,抛光间隙越小,液动压力和黏性切应力就越大。且越小的间隙产生的液动压力与黏性切应力的稳定区域越大,更有利于材料的均匀去除。
根据数值模拟结果,结合K9玻璃工件尺寸15 mm×15 mm×2 mm,选定圆柱辊子直径和长度均为30 mm;在保证去除作用能够成功进行的前提下,为使得材料均匀去除,抛光辊子转速不宜过高;而对于抛光间隙,该参数数值越小越有利于试样表面材料的均匀且高效去除。
3 实验研究
3.1 抛光实验
线性液动压抛光实验平台如图7所示,该抛光平台在沧州聚航隔振设备有限公司生产的JG-JM-12-08型精密光学平台上进行组装,可实现抛光辊子的回转以及在X、Y方向上的平移运动,工件在Y方向上的往复运动以及在X方向上的微米级调节。抛光加工时,抛光辊子与工件浸没于抛光液中,抛光辊子随电主轴高速旋转,同时直线电机带动工件在Y方向进行匀速往复平移运动,并能够与抛光辊子保持一个稳定的间隙值距离。
实验流程如图8所示,将工件用无水乙醇超声清洗3 min,清洗完成后风干工件。将工件盘置于加热台上,待温度上升至90 ℃后取适量石蜡融于工件盘并完成工件贴片,用精密研磨盘完成压片操作以确保石蜡均匀分布。待工件盘冷却后将其安装于直线电机上,然后借助角度和间隙调节机构完成工件面的调平以及控制工件与抛光辊子的间隙。设置直线电机的往复运动程序与电主轴(即辊子)的转速,将抛光液倒入抛光槽至适当液位。运行直线电机程序并启动电主轴,此刻即正式开始线性液动压抛光;待抛光加工一定时间后,关闭直线电机与电主轴,结束抛光。取下工件盘并在清水下冲洗,去除其表面残留的抛光液;加热工件盘至可取下工件,然后将工件分别用丙酮、无水乙醇、超纯水超声清洗3 min,烘干后放入工件盒待测试。采用中图仪器公司所生产的Super-view W1系列光学3D表面轮廓仪测量抛光工件表面粗糙度数值和表面微观形貌。
为更深入了解线性液动压抛光工艺的加工特性,获取更加优异的表面形貌,采用单因素实验探究抛光表面形貌的演变规律,实验条件见表3。
3.2 表面微观形貌的演变规律
选取辊子转速为12 000 r/min、抛光间隙为40 μm,依照图8所述的操作步骤进行线性液动压抛光加工实验,抛光时间t分别设置为20 min、40 min、60 min和80 min,获得对应的表面粗糙度Rt数值变化情况如图9所示。随着抛光时间的增加,工件表面粗糙度Rt的数值不断减小,60 min后达到稳定状态,达到1.81 nm。
图10显示了不同抛光时间下工件表面采样轮廓点高度和3D显微表面形貌,相应3D显微表面形貌充分表明了工件表面采样轮廓点高度特征。对比轮廓高度箭靶图可以看出,进行线性液动压抛光加工之前,工件表面质量较差,工件表面上存在大量分布明显的“凸峰”特征,工件表面采样轮廓点高度主要集中在2~6 nm的分布区间。而当开始进行抛光加工后,“凸峰”特征被不断去除,工件表面采样轮廓点的高度逐渐减小。在经过60 min抛光加工后,此时抛光工件表面的微观缺陷已基本消失,轮廓点高度主要集中在1 nm附近,轮廓点最大高度也已经降低到了1.8 nm的水平,工件表面形貌得到明显的改善。
3.3 抛光工艺参数的影响规律研究
选取抛光时间固定不变且为60 min,根据数值模拟结论,抛光间隙和抛光辊子转速会影响液动压力与黏性切应力的大小与均匀性,从而影响最终的抛光效果,因此选取抛光辊子转速n和抛光间隙h0作为实验参数。考虑到随机误差对实验最终结果的干扰,每组单因素实验同时加工3块工件,每块工件随机测量3个点的Rt值,最后取该3块工件的9个测试值求平均值并作为每组实验抛光后的Rt有效值。根据数值模拟结论以及实际加工条件,各工艺参数水平选取结果见表4。每组单因素实验均控制其他参数处于水平2,绘制各工艺参数水平影响Rt值的曲线图以及影响轮廓高度的箭靶图,见图11~图13。
实验结果与前文数值模拟结果一致。由图11a和图12可知,抛光辊子转速的增大会在一定程度上减小抛光表面粗糙度Rt的数值,轮廓点高度逐渐集中在1 nm附近,但当转速由16 000 r/min增大到20 000 r/min时,会使液动压力和黏性切应力分布的均匀性降低,反而不利于材料的均匀去除,最终会导致粗糙度Rt的数值不降反增,轮廓点分布也更差。由图11b和图13可知,抛光间隙越小,液动压力和黏性切应力的大小和分布的均匀性越好,越有利于工件表面材料的均匀且高效去除,因此粗糙度Rt的数值越小,轮廓点分布愈加集中于较低高度,表面形貌越好。
4 结论
(1)依据动压润滑理论阐释了线性液动压抛光流场中产生液动压力的原理;通过对流场中抛光作用力的分析阐述了抛光表面形貌的演变机制,即液动压力将磨粒压向工件表面,然后在高速流体的带动下对工件表面材料进行冲击以达到去除作用。
(2)借助FLUENT软件对抛光流场进行了数值模拟研究,分析讨论了抛光辊子尺寸以及抛光工艺参数对抛光区域液动压力和黏性切应力的大小及分布均匀性的影响规律,结论如下:辊子直徑和辊子转速的增大都会使得液动压力和黏性切应力的数值增大,但分布均匀性会下降,不利于材料的均匀去除。抛光间隙值越小,液动压力和黏性切应力越大,分布均匀性越好。抛光辊子的长度过短或过长都不利于材料的均匀去除。
(3)采用自制的线性液动压抛光实验平台,以K9玻璃为实验对象,结合理论分析和数值模拟,探究抛光加工表面形貌和表面粗糙度的创成过程。抛光辊子转速的增大会在一定程度上减小抛光表面粗糙度Rt的数值,但当转速过高时,会使液动压力和黏性切应力分布的均匀性降低,反而不利于材料的均匀去除,最终会导致粗糙度Rt的数值不降反增,轮廓点分布更差,表面形貌也更差。抛光间隙越小,液动压力和黏性切应力的大小和分布的均匀性越好,越有利于工件表面材料均匀而高效地去除,从而使粗糙度Rt的数值越小,轮廓点分布愈加集中于较低高度,表面形貌越好。
参考文献:
[1] MA Zhanlong, LIU Jian, WANG Junlin. Development and Application of Ultra-smooth Optical Surface Polishing Technology[J]. Laser & Optoelectronics Progress, 2011, 48(8):082202.
[2] 袁巨龙, 毛美姣, 李敏, 等. 基于响应曲面法的YG8硬质合金刀片化学机械抛光工艺参数优化[J]. 中国机械工程, 2018, 29(19):2290-2297.
YUAN Julong, MAO Meijiao, LI Min, et al. Optimization of Process Parameters for Chemical Mechanical Polishing of YG8 Cemented Carbide Inserts Based on Response Surface Methodology [J].China Mechanical Engineering, 2018, 29(19):2290-2297.
[3] MORI Y, YAMAUCHI K, ENDO K. Elastic Emission Machining[J]. Precision Engineering, 1987, 9(3):123-128.
[4] MORI Y, YAMAUCHI K, ENDO K. Mechanism of Atomic Removal in Elastic Emission Machining[J]. Precision Engineering, 1988, 10(1):24-28.
[5] SU Y T, WANG S Y, HSIAU J S. On Machining Rate of Hydrodynamic Polishing Process[J]. Wear, 1995, 188(1/2):77-87.
[6] NAMBA Y, OHNISHI N, YOSHIDA S, et al. Ultra-precision Float Polishing of Calcium Fluoride Single Crystals for Deep Ultra Violet Applications[J]. CIRP Annals, 2004, 53(1):459-462.
[7] WATANABE J, SUZUKI J, KOBAYASHI A. High Precision Polishing of Semiconductor Materials Using Hydrodynamic Principle[J]. CIRP Annals, 1981, 30(1):91-95.
[8] PENG W Q, DENG X, LUO Z B, et al. A Nano-imprint Method Analysis of the Optical Subsurface Quality Processed by Hydrodynamic Effect Polishing[J]. Optik, 2018, 171:71-76.
[9] WEN D H, PIAO Z Y, ZHANG T H. A Hydrodynamic Suspension Polishing Method for Ultrasmooth and Low-damage Surface[J]. Precision Engineering, 2016, 46:278-287.
[10] 郑子军, 李攀星, 蔡东海, 等. 液动压悬浮抛光流场的数值模拟及抛光工具盘结构优化[J]. 中国机械工程, 2019, 31(6):638-643.
ZHENG Zijun, LI Panxing, CAI Donghai, et al. Numerical Simulation of Hydrodynamic Suspension Polishing Flow Field and Optimization of Poli-shing Tool Plate Structure[J].China Mechanical Engineering, 2019, 31(6):638-643.
[11] CAO Z C, LIN B, JIANG X M, et al. Flow Field Analysis of the Thin Fluid Film in Disc Hydrodynamic Polishing[J]. Procedia CIRP, 2018, 77:363-366.
[12] 付有志,路家斌,阎秋生,等.磁流变动压复合抛光基本原理及力学特性[J].表面技术,2020,49(4):55-63.
FU Youzhi, LU Jiabin, YAN Qiusheng, et al. Basic Principle and Mechanical Property of Magnetorheological Hydrodynamic Compound Polishing[J]. Surface Technology, 2020, 49(4):55-63.
[13] JADHAO V, ROBBINS M O. Rheological Properties of Liquids under Conditions of Elastohydrodynamic Lubrication[J]. Tribology Letters, 2019, 67(3):1-17.
[14] JIANG Y, XU B, LU X, et al. Multiscale Simulation of Flow in Gas-lubricated Journal Bearings:A Comparative Study between the Reynolds Equation and Lattice Boltzmann Methods[J]. Engineering Applications of Computational Fluid Mechanics, 2021, 15(1):1792-1810.
[15] BAYADA G, CHAMBAT M. The Transition between the Stokes Equations and the Reynolds Equation:A Mathematical Proof[J]. Applied Mathematics and Optimization, 1986, 14(1):73-93.
[16] 文東辉, 许鑫祺, 郑子军. 线性液动压抛光流场的剪切特性研究[J]. 中国机械工程, 2021, 32(18):2203-2210.
WEN Donghui, XU Xinqi, ZHENG Zijun. Study on Shear Characteristics of Flow Field in Linear Hydrodynamic Polishing[J]. China Mechanical Engineering, 2021, 32(18):2203-2210.
[17] 郑子军, 薛凯元, 文东辉, 等. 线性液动压抛光加工的流体动压特性研究[J]. 中国机械工程, 2020, 31(8):907-914.
ZHENG Zijun, XUE Kaiyuan, WEN Donghui, et al. Study on Hydrodynamic Characteristics of Linear Hydrodynamic Polishing[J].China Mechanical Engineering, 2020, 31(8):907-914.
