山区峡谷风袭击下绝缘子串风偏特性研究

2023-12-01雷凌志宋传兴

三峡大学学报(自然科学版) 2023年6期

汪峰雷凌志宋传兴

(1.三峡大学土木与建筑学院, 湖北宜昌 443002;2.三峡大学电气与新能源学院, 湖北宜昌 443002)

山区架空输电线路易遭受峡谷风袭击,严重时甚至会引起线路绝缘子串风偏失效,诱发风偏闪络事故[1].2020年我国四川、贵州等地山区发生了大规模停电事故,2021年国家电网青海电力公司750 k V 月海Ⅰ、Ⅱ线受大风袭击发生风偏事故.

针对山区峡谷风场模拟问题,陈科技等[2]在平坦地形下利用谐波叠加法模拟了6种湍流度的脉动风场.沈炼等[3]基于CFD 与WRF 耦合模式对峡谷风场进行精细化分析.严磊等[4]基于大涡模拟法对川藏线一处峡谷风场特性进行了模拟和分析.骆光杰等[5]基于卡曼脉动风功率谱,采用谐波叠加法模拟了脉动风速时程.闫波等[6]开展了架空输电线路段随机风场数值仿真分析.兰冰姬等[7]采用谐波叠加法模拟了脉动风荷载时程.

针对风场作用下绝缘子风偏角和电气间隙问题,卢永玲等[8]计算了绝缘子串风偏角和二维模型下最小风偏间隙.周磊等[9]给出了一种考虑脉动风效应的悬垂绝缘子串风偏角计算方法.石天如等[10]基于悬垂绝缘子串的刚体直杆模型,考虑降雨强度下允许最小间隙,计算了导电体向杆塔放电的临界最小间隙.鲍华等[11]考虑风荷载和导体自重的综合作用,推导了绝缘子串风偏角计算公式.赵淑贞等[12]提出了一种简化的计算方法,用于确定输电线路塔杆悬挂绝缘子串的峰值动态风阻偏航角.安立强等[13]分析了输电线路的风偏闪络特性.张志劲等[14]探究了台风作用下绝缘子串风偏角动态风偏特性及影响因素.肖林海[15]以悬垂绝缘子串为研究对象采用脉动放大系数修正方法,给出了不同风速下脉动增大系数,楼文娟等[16]采用了风荷载调整系数,给出了不同条件下风荷载调整系数的取值.由此可知,良态风场作用下的绝缘子风偏角计算主要有两种方法:一是以架空输电线规范计算结果为基础,计入脉动风放大系数;二是计算风荷载时引入风荷载调整系数.

上述研究为输电线路绝缘子串的风偏特性研究奠定了坚实的基础.但既往的研究主要是针对良态风场作用下的绝缘子串风偏,目前对于非良态的峡谷风场作用下绝缘子串风偏摆动特性尚不明确,有待进一步研究.因此,本文提出一种新的峡谷风风场模拟方法,构建输电线路塔线体系有限元模型,分析峡谷风场袭击下绝缘子风偏特性,研究雨荷载和风攻角等因素对风偏的影响规律,探索了峡谷风增大效应,给出了峡谷风袭击下绝缘子串风偏计算公式.研究结果为山区峡谷地区输电线路风偏设计与计算提供理论依据.

1 山区峡谷风数值模拟

1.1 谐波叠加法及功率谱密度函数

基于Davenport脉动风功率谱,采用简谐波叠加法模拟线路的峡谷风场是目前常用的思路.Davenport脉动风功率谱是通过全球各个地区观测点处所测得的强风记录所建立,其表达式为

式中:Sv(f)为脉动风速功率谱(m2/s);k为地面粗糙度系数;v10为10 m 高度处的平均风速;f为脉动风频率.

基于离散谱无限接近目标随机过程功率谱的离散数值模拟方法[17],对于具有n个零均值的平稳高斯过程vj(t)(j=1,2,…,n),风速的谱密度函数矩阵为

式中:S(f)是正定矩阵,其中的每一个元素是相关函数的傅里叶变换,根据Cholesky分解S(f)可分解为

模拟的脉动风风速为

式中:|Hjk(fl)|为下三角矩阵元素的模;Δf=(fu-fd)/N,为频率增量;θjk(fl)为两个不同作用的点之间的相位角;…,N;fu为截取频率上限;fd为截取频率下限;θl为(0,2π)均匀分布的随机相位角;N为频率采样点数,取值越大越精确.

1.2 峡谷风场功率谱相关性分析

基于文献[18-19]现场实测峡谷风特性,对峡谷风场进行测量.测量风速杆塔所在位置位于峡谷风口处,在杆塔高度为10、20、30、35 m 处各安装一个二维机械风速仪,在杆塔高45 m 处安装一个三维超声风速仪,风速仪均采用24 h工作模式,布置位置如图1所示.三维超声风速仪采样频率为3 Hz,风速测量范围为0～90 m/s,精度为±1%,风向角测试范围0°～360°,精度为±3%;二维机械风速仪采样频率1 Hz,风速测试范围0～110 m/s,精度为±0.5 m/s,风向角的测试角度范围为0°～360°,精度范围为±4°.

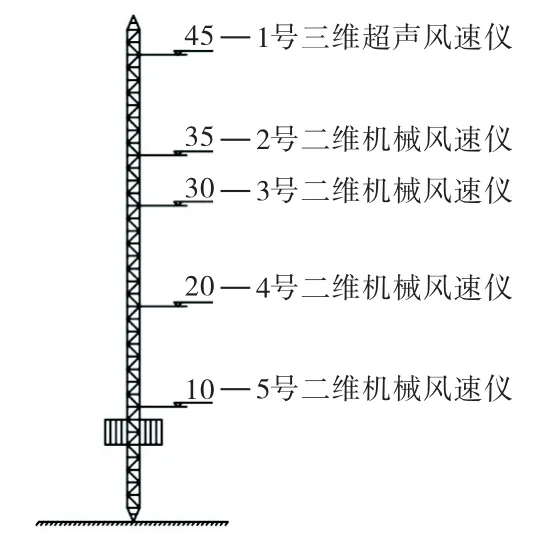
图1 风速测量塔及风速仪布置

脉动风功率谱密度是研究脉动风速的重要统计特征,表示紊流动能在各频率分布密度,利用Fourier快速变换得到峡谷风样本的脉动风速功率谱密度,对同一高度不同时间段取其平均值可以得到平均功率谱,可以在一定程度上降低离散Fourier变化带来的误差.峡谷风样本平均功率谱密度曲线及其理论模型如图2所示.

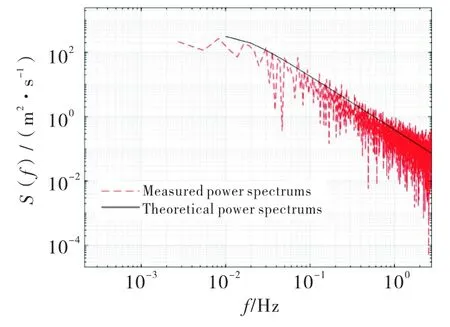
图2 实测功率谱与理论谱

由图2可知,Davenport谱与实测功率谱吻合度较差.说明未修正的标准风Davenport谱模拟峡谷风精度差,若要准确模拟山区峡谷风,需要结合峡谷风的实测数据对标准Davenport谱进行系数的修正.

1.3 基于实测峡谷风的Davenport谱修正

为使Davenport谱能够更好地反映出峡谷地区的实际风特性,提出一种对Davenport谱进行修正的方法,利用峡谷地区实测数据确定表达式待定系数,让修正之后的风谱包含了峡谷地区的客观变化规律和信息.定义修正Davenport谱的表达式为

式中:R1、R2、R3、R4、R5为待定系数.

根据所测得峡谷风风速数据可得到峡谷地区风速功率谱,根据功率谱得出求解修正Davenport谱系数所需频率和功率值,然后基于最小二乘法的非线性拟合可以求解得到修正Davenport谱的待定系数.

定义其初值为R0=[R10,R20,R30,R40,R50],将初值代入式(5)得到γ0,则待定系数的求解如下.

对函数(5)在R0点处进行Taylor级数展开,不计高阶项目,其近似一阶表达式为

式中:ϑi=Ri-Ri0,i=1,2,3,4,5;j=1,2,…,n,为最小二乘法拟合时所需数据点数序号;γj0为序号j数据点的初始函数值.

建立近似线性关系待求系数的非线性函数表达式为

对式(7)求其偏导令其值等于零,见式(8)

然后将n个数据点代入式(8),建立超定方程组为

式中:G=(g1,g2,g3,…gn);D=(d1,d2,d3,d4,d5);H=(h11,…,hn1,h12,…,hn2,h13,…,hn3,h14,…,hn4,h15,…,hn5).求解得出超定方程组D的值就是最小二乘解.

求得待定系数为

对于非线性函数(5)的近似线性形式(6)可采用多元线性拟合的方法进行求解,在一定程度上降低了计算的复杂性.由于所采用的方法为近似线性形式,在进行初步计算时存在少许误差.为了计算的准度,需要将求解所得值作为初始值进行多次求解,直到满足所需精度要求.

对于修正Davenport谱模型,以上文某地峡谷实测风速为样本,计算得到频率值和功率值作为最小二乘法求解数据点,选取待定系数初始值为R0=[1,1.2,1.2,1.5,1.3],利用上式计算得到系数值为R1=0.435 6,R2=0.8476,R3=0.6934,R4=1.2540,R5=0.956 4.将该系数代入式(5)可得到修正Davenport谱:当考虑3个修正参数R1、R2、R3时得到修正Davenport谱,如图3(a)所示;考虑4 个修正参数R1、R2、R3、R4时得到修正Davenport谱,如图3(b)所示;考虑5个修正参数R1、R2、R3、R4、R5时得到修正Davenport谱,如图3(c)所示.

图3 实测功率谱与修正参数理论谱

由图3可知,实测生成的峡谷风风速谱与考虑5个修正参数后的Davenport谱吻合最好,验证了本文方法的合理性,可实现架空输电线路峡谷风场模拟.

2 塔线体系有限元模型建立

以某跨越山区的500 k V 大跨越输电线路为例,杆塔主材采用Q420B型角钢,斜材采用Q345B 型角钢,辅材采用Q235B型钢材,钢材密度为7 800 kg/m3,泊松比为0.3,弹性模量为206 GPa.采用ANSYS结构有限元软件建立三跨连续档有限元模型,考虑杆塔-绝缘子串-输电线之间相互作用.绝缘子和导线参数见表1～2.

表1 绝缘子结构参数

表2 导线参数

2.1 塔线体系有限元模型

由于绝缘子采用了复合绝缘子串(FXBW-500/160-3),其材料刚度比较小,在风荷载的作用下弯曲变形较小,因此采用Beam188单元模拟.同时,为了确保结果的准确性,沿长度方向将绝缘子划分为多个单元.

导线为悬索结构,一般状态下只受拉而不受压,因此采用LINK10索单元进行模拟.导线建模时需要确定其只受重力时的初始线形,采用迭代法找形分析,设置较小的初始应变后,打开NLGEOM 命令和SSTIF命令选项,在导线跨中单元水平张力和设置的初始张力偏差在5%内,则满足收敛要求,完成输电线在自重状态下的找形.

选用桁梁混合模型构建输电塔杆有限模型[20],该模型考虑杆塔主材料的梁单元特征和各个斜材主要承受的轴向力及其桁架刚性的同时,较为合理地避开了平面节点之间的问题.主材料以及横隔材料同时承受轴力也承受弯矩和剪力,可以视作梁单位,采用ANSYS单元库中的Beam188单元模拟;斜材承受轴向的力视作杆单元,用Link8单元模拟.有限元模型如图4所示.

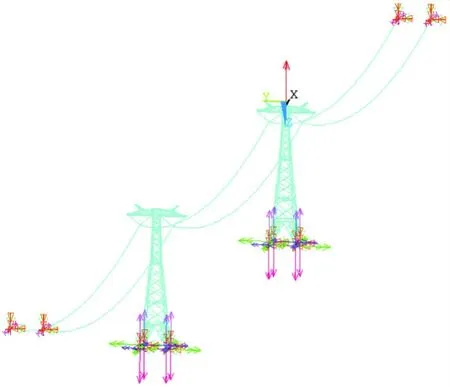
图4 500 k V 输电杆塔-绝缘子串-导线耦合模型

绝缘子和横担之间、绝缘子和输电导线之间采用球铰的方式连接,耦合方式选取铰接,保证绝缘子串风偏时能自由摆动;杆塔塔角处采用全部约束形式;输电导线两端采用固定约束方式限制其位移.

2.2 峡谷风荷载施加

由于存在不均匀湍流,在不同高度和位置情况下,模拟点风速和相位都会有所不同,因此假设脉动风为零均值的高斯平稳随机过程,脉动风风速进行时程模拟时,假设不同高度的质点风速在脉动风作用下时相干,对于同一时间点,脉动风可以同时作用在结构上的所有点.

某地峡谷的最大风速达33.46 m/s,在10 m 高处的风速为12.62 m/s,峡谷的脉动风载作用于距离地面高度为20 m 的绝缘子串.该线路场地为C类,不同高度的平均风速按C 类地貌的风剖面取值,地面粗糙系数k为0.012 91,峡谷风谱作用时间为400 s,采样点数取2 000 个,模拟点数为40 个,时间步长为0.01 s,截断频率为8π,频率步长为(π/250),采用Davenport空间相干函数.图5是运用上述理论方法模拟出的峡谷某点风速时程v(t)曲线.

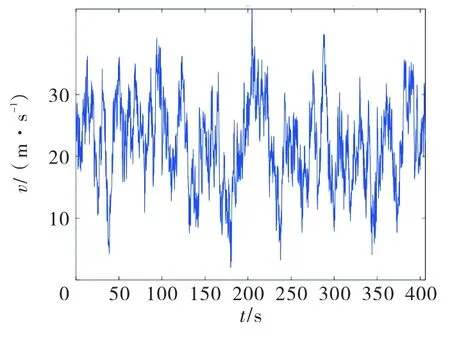
图5 峡谷风风速时程

图6 杆塔-串-线体系所受峡谷风荷载作用

由图5可知,某高度处的峡谷风风速时程呈现随机性,并在风速均值附近上下波动.

已知风速时程后,可将风速转化为绝缘子串、杆塔以及导线的风荷载,并施加到有限元模型的节点上.绝缘子串中间位置所受横向水平风荷载GH[21]为

式中:n为绝缘子串数量;A为绝缘子串的迎风面积(m2);μH为风压高度变化系数;g为重力加速度,取值9.806 65 N/kg;vf与架空输电线路所处的高度H、离地面10 m 高的3秒风风速v(m/s)以及地面粗糙度指数μ有关,见式(12)

地面粗糙度μ取0.15,μH在不同粗糙度类别下不同高度的部分取值见表3.为了适应不同高度的杆塔情况,在4 类不同地面的粗糙度下以高度为自变量,对μH在杆塔高度5～100 m 之间的取值进行函数拟合.

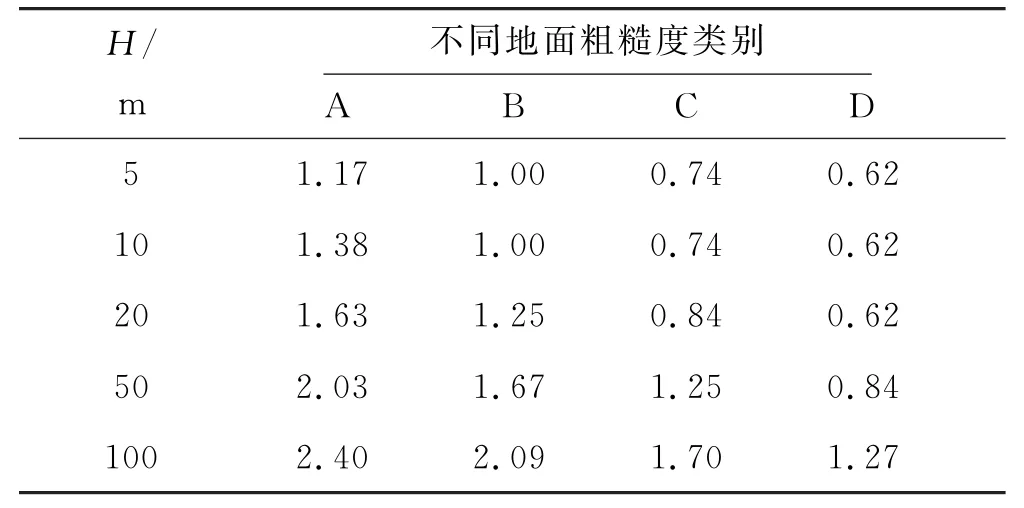
表3 u H 取值表

绝缘子串下端所受的水平风荷载WH为

式中:α为风压不均匀系数,取值0.61;K为与绝缘子串相连导线的体型系数,当线径＜17 mm 时,取1.2,当线径＞17 mm 时,取1.1;γ为风向与输电导线夹角,取30°;d为与绝缘子串相连导线外径(mm);LH为导线水平档距(m).

杆塔所受风荷载PS为

式中:βZ为输电杆塔风荷载调整系数;v为风速(m/s);Ar为构件所受风压投影面积(m2),按照式(15)取值.

式中:γ为输电杆塔的填充系数,根据设计规范取值[22],宽度较大的可取0.15～0.20,取值0.2;h为计算高度(m);x1、x2为杆塔塔身计算段的上宽度和下宽度(m).杆塔-串-线体系所受峡谷风荷载作用如图6所示.

为了避免风偏动态分析过程中出现突然施加风荷载而引起瞬态变化,故先施加平均风荷载,然后再施加脉动风荷载.其中绝缘子、输电导线上的风荷载根据单元数平均施加到各个节点上,所施加的节点力如式(13)～(15)所示,输电杆塔风荷载施加在每个塔段迎风面的6个节点上.

3 绝缘子风偏特性分析

3.1 峡谷风袭击下风偏角时程特性

脉动风和平均风作用下该线路的绝缘子风偏角分别为θav、θ*.绝缘子串风偏角时程如图7所示.

图7 峡谷风袭击下绝缘子风偏角时程

由图7可知,在峡谷风袭击下,绝缘子风偏角围绕着均值呈现上下波动.进一步得到绝缘子风偏角分布情况,如图8所示.

由图8可知,峡谷风作用时绝缘子风偏角分布呈现正态分布.该输电线路的绝缘子风偏角在60°分布的概率最大,其概率为22%.

峡谷风属于自然风的组成部分,其作用周期一般很长且作用强度随着时间随机变化,对结构的作用拥有动力学性质,使得输电线路响应放大.采用刚体直杆法没有考虑到风的这一特性,在峡谷风的基础上,分析峡谷风对绝缘子串风偏角的动力放大效应.根据统计学知识和随机振动学理论,风偏角代表值是均值和均方差的函数[23],表达式如下:

3.2 雨荷载对动态风偏角的影响

复杂风雨条件下对绝缘子串有不可忽略的影响,降雨条件下雨荷载作用力表达式为[24]

假设峡谷中雨滴下落的方向与峡谷风一致,主要研究顺风速下雨荷载对绝缘子串的作用.Vt为峡谷风风速,取值考虑风速对雨滴速度的影响,ψ为某一降雨强度等级下单位体积空气中雨滴所占百分比;ρ为雨滴密度,与水的密度相同;b为绝缘子串的等效宽度,这里取值为其盘径.ψ为不同降雨条件下单位体积空气中所含雨滴百分比,见表4.

依据绝缘子的风偏角时程特性,考虑峡谷降雨工况,选择暴雨(中)、暴雨(强)、暴雨(极大)作为降雨条件,并与峡谷风风荷载侵袭下的结果进行对比分析,见表5.

表5 不同降雨条件下的风偏角[单位:(°)]

由表5 可知,绝缘子风偏角与降雨强度呈正相关,降雨强度越大风偏角越大.相比于单一的峡谷风作用,考虑降雨条件的绝缘子串风偏角大于单一峡谷风作用时的风偏角,极大暴雨时风偏角增大幅值达到了9.97%.

基于有限元模型计算获得了不同降雨工况下绝缘子串动态风偏角时程,如图9所示.

由图9可知,在峡谷风和大暴雨的作用下,绝缘子串的风偏角最大.说明峡谷风和大暴雨的作用工况是风偏计算的最不利工况.

3.3 风攻角对动态风偏角的影响

为了研究风攻角对绝缘子串风偏特性的影响,对不同风攻角下绝缘子串线体系进行仿真模拟计算(仿真条件:风速30 m/s、档距400 m、高差0 m、风攻角由-30°～30°变化).不同风攻角下绝缘子串稳态和峡谷风风偏角响应计算结果对比见表6.风攻角为负表示风向与水平面的夹角为俯角,仰角为正.

表6 绝缘子串稳态风和脉动风风偏角计算结果对比

由表6可知,在不同风攻角作用下,绝缘子串风偏角平均值与平均风作用下的稳态风偏角相差不到1°.绝缘子串风偏角代表值与风攻角呈线性关系,且为正相关,风攻角越大风偏角代表值越大.^θ与θ*的差值随着风攻角增大而增大.改变风攻角大小时,随着风攻角增大绝缘子串风偏角的均方差缓慢增大.风攻角由-30°～30°变化时,其方差由2.32 增加至3.32,当风攻角数值增大时,绝缘子串风偏角波动性明显增强.

4 峡谷风动力增大效应

在峡谷地区线路中,由于线路条件改变,悬垂绝缘子风偏特性也会有所改变,考虑不同高差条件对悬垂绝缘子串的风偏影响.高差的计算示意图如图10所示,记悬垂绝缘子两侧高差分别为h1、h2,高差为正表示两侧绝缘子悬挂点高于中间,为负表示两侧的悬垂绝缘子悬挂点低于中间.

图10 高差计算示意图

为探究悬垂绝缘子风偏特性受高差影响情况,对不同高差情况下的绝缘子串线体系进行模拟仿真计算(模拟仿真条件:风速25 m/s、档距400 m、风攻角0°),模拟计算其所受脉动风大小,并计算所受峡谷风侵袭下的风偏角,结果见表7,同时列出了峡谷风平均静力风下的风偏角θav.

表7 不同高差下风偏角

由表7可知,峡谷风侵袭下绝缘子串风偏角相对于静力风偏角有所增大.因此,采用刚体直杆法进行绝缘子串风偏角度理论计算时,可定义风偏增大效应系数ε,如(18)所示,以便考虑峡谷风的动力增大效应的影响.峡谷风动力增大效应系数为

当高差不同时,峡谷风偏相对于静力风偏的增大系数见表8.

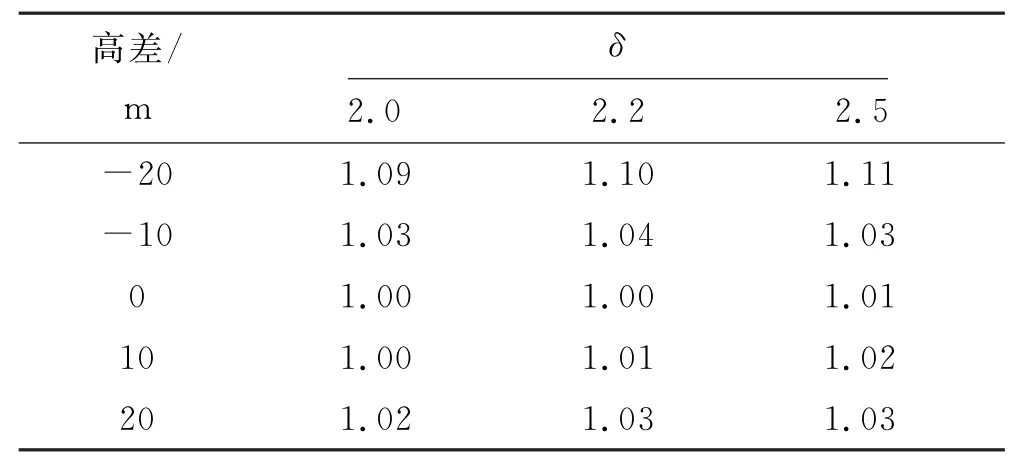
表8 不同高差下的脉动增大系数ε

由表8 可见,在峡谷处25 m/s风速下ε均在1.01～1.11.对山区峡谷风速分别为30和35 m/s时候的情况进行相同分析,并取ε的平均值,得到在风速、保准概率不同情况下山区峡谷风袭击绝缘子串风偏角脉动增大系数,见表9.

表9 风速、保准概率不同时的脉动增大系数ε

进行峡谷绝缘子串风偏角计算时,考虑到峡谷风脉动风动力效应,需要将规范公式中的风偏角乘以脉动增大系数即可[25].因此,计算山区峡谷风袭击下500 k V 输电线路绝缘子串风偏角,采用刚体直杆法时,修正后风偏角计算公式可表示为

式中:λH为绝缘子串底部到顶部的水平距离;λV为绝缘子串底部与顶部的竖向距离;ε为峡谷风动力增大效应系数;η为风偏放大系数,风速为20、30、40 m/s时,绝缘子的放大系数分别为1.22、1.17、1.12,其它取值可采用插值法;GV为绝缘子串自身的重力(N);WV为输电导线的重力(N);WZ为绝缘子串底部所悬挂的重锤重力(N).

由表9可知,峡谷风的增大效应系数ε大于1,由式(19)计算峡谷风作用的绝缘子串风偏角比原有规范计算值要大.也说明针对峡谷袭击下绝缘子串风偏角的计算,我国输电线线路设计规范中计算值偏小,不利于线路的安全设计.因此,峡谷风袭击下绝缘子串的风偏角计算,建议考虑峡谷动力增大效应,宜采用式(19)进行适当修正.