基于向量加权算法优化ELM的变压器故障诊断

曹鹏飞，甘永平

（北京国网信通埃森哲信息技术有限公司，北京 100053）

引言

电力变压器是一种用于改变交流电电压的装置[1]，被广泛应用于电力、制造加工业和航空航天等重要领域。而随着变压器设备的长时间运行，故障率也会随之提高，。因此，针对变压器设备进行运行工况实时监测与故障诊断具有重要意义[2]。采用故障诊断技术可以有效降低由变压器故障导致的事故发生概率，但这同时要求所使用的故障诊断技术具有相当高的诊断精度[3]。

目前，绝大部分输配电系统中的变压器设备都是油浸式变压器[4]。油中溶解气体分析法（DGA）是广泛使用的变压器故障诊断方法之一[5]，主要包括[6]：特征气体法、比值法以及大卫三角形法等。这些传统方法大多依赖专家先验知识，专家知识又难以覆盖所有可能发生的故障情况[7]。随着数据驱动技术的提出，学者们将人工神经网络（ANN）[8]、支持向量机（SVM）[9]、随机森林（RF）[10]等数据驱动方法应用在变压器故障诊断领域中。文献[11]提出了一种多策略海鸥优化算法（SOA）优化SVM的变压器故障诊断方法，使用多策略的改进方法提升SOA的寻优性能，优化SVM内部参数，提升了诊断精度。文献[12]通过修改灰狼算法的控制因子和加权距离，提高了算法的收敛精度和稳定性，并结合概率神经网络进行变压器故障的有效诊断。文献[13]采用ReliefF和最大相关最小冗余（mRMR）算法对变压器故障数据进行特征选取，再通过改进天鹰优化算法（IAO）对最优特征集合和SVM参数联合寻优，构建最佳故障诊断模型，提高了变压器故障诊断精度。

ELM相较于其他神经网络模型效率更高，它通过固定随机产生的权值和偏置来进行训练学习，而不需要反馈调整，大大减少了训练时间。但这同时也导致权值和偏置随机选择的不合理性，因此选择合适的智能优化算法进行优化对提升ELM分类精度有重要作用。文献[14，15]分别采用粒子群算法和黏菌算法对ELM参数进行优化，但其在解空间内的全局搜索和收敛速度方面仍有一定的缺点，并且容易陷入局部最优的情况也没有得到解决，这会对ELM的分类精度有一定影响。本文提出一种采用INFO算法优化ELM的变压器故障诊断模型，首先使用INFO算法对ELM的初始权值和偏置进行寻优，然后将变压器油中溶解气体作为输入参数，输出故障分类编码，然后使用提出的INFO-ELM算法建立变压器故障诊断分类模型，并进行仿真实验，同时与SVM、ELM、PSO-ELM、SSA-ELM、GWO-ELM故障诊断模型进行诊断效果对比测试，验证所提出算法的有效性。

1 INFO算法及性能测试

1.1 INFO基本原理

向量加权平均算法（INFO）是一种基于群体的优化算法，该算法包括更新规则、向量合并和局部搜索三个阶段，具体原理如下：

1）更新规则阶段。使用基于均值的规则（MeanRule）更新向量的位置，是从一组随机向量的加权均值中提取的。此外，为了提升算法的全局搜索能力，在更新规则阶段中加入了收敛加速部分（CA）。更新规则的主要公式如下：

式中：

和—第g次迭代得到的新位置向量；

σ—向量的缩放率，可以由公式（2）得出；

a1≠a2≠a3≠1—[1，NP]区间中随机选取得到的不相同的整数；

randn—标准正态随机值。

式中：

α—可以通过公式（3）进行更新。

针对MeanRule的定义如公式（4）所示：

式中：

r —[0，0.5]区间内随机选取的1个数。

式中：

式中：

式中：

w1，w2，w3—加权函数，用来计算向量的加权平均值，能够增强算法在解空间内的全局搜索能力；

xbs，xbt，xws—种群第g次迭代时最优、次优和最差的解向量。

2）向量合并阶段。根据公式（18），INFO把上一阶段的两个向量()与rand ＜ 0.5的向量结合生成新向量。

式中：

—第g次迭代后的向量合并所得的新向量；

µ=0.05×randn。

3）局部搜索阶段。通过局部搜索阶段可以避免算法陷入局部最优的情况。如果rand ＜ 0.5，则可以生成一个新向量。其中rand是[0，1]中的随机数。

式中：

式中：

φ—区间（0，1）中的一个随机数；

xrnd—是由xavg、xbt和xbs组成的新解，这样做可以增强算法的随机性，从而更好的在解空间中进行搜索；v1和v2是两个随机数，定义如下：

1.2 INFO算法寻优性能测试

为了测试INFO算法的寻优能力，选择常用的23个标准测试函数中的F1（单峰函数/30维）、F9（多峰函数/30维）和F20（固定维度多峰函数/6维）作为性能对比测试函数，如表1所示。

表1 性能对比测试函数

本文采用PSO、GSA、SCA和GWO四种优化算法进行性能比较，对所有优化算法设置相同的初始化参数：种群规模设置为30，最大迭代次数设置为500，算法运行次数设置为30次。测试结果如图1～3所示。由图1～3可知，INFO算法具有更好的寻优性能。

图1 函数F1(x)寻优曲线

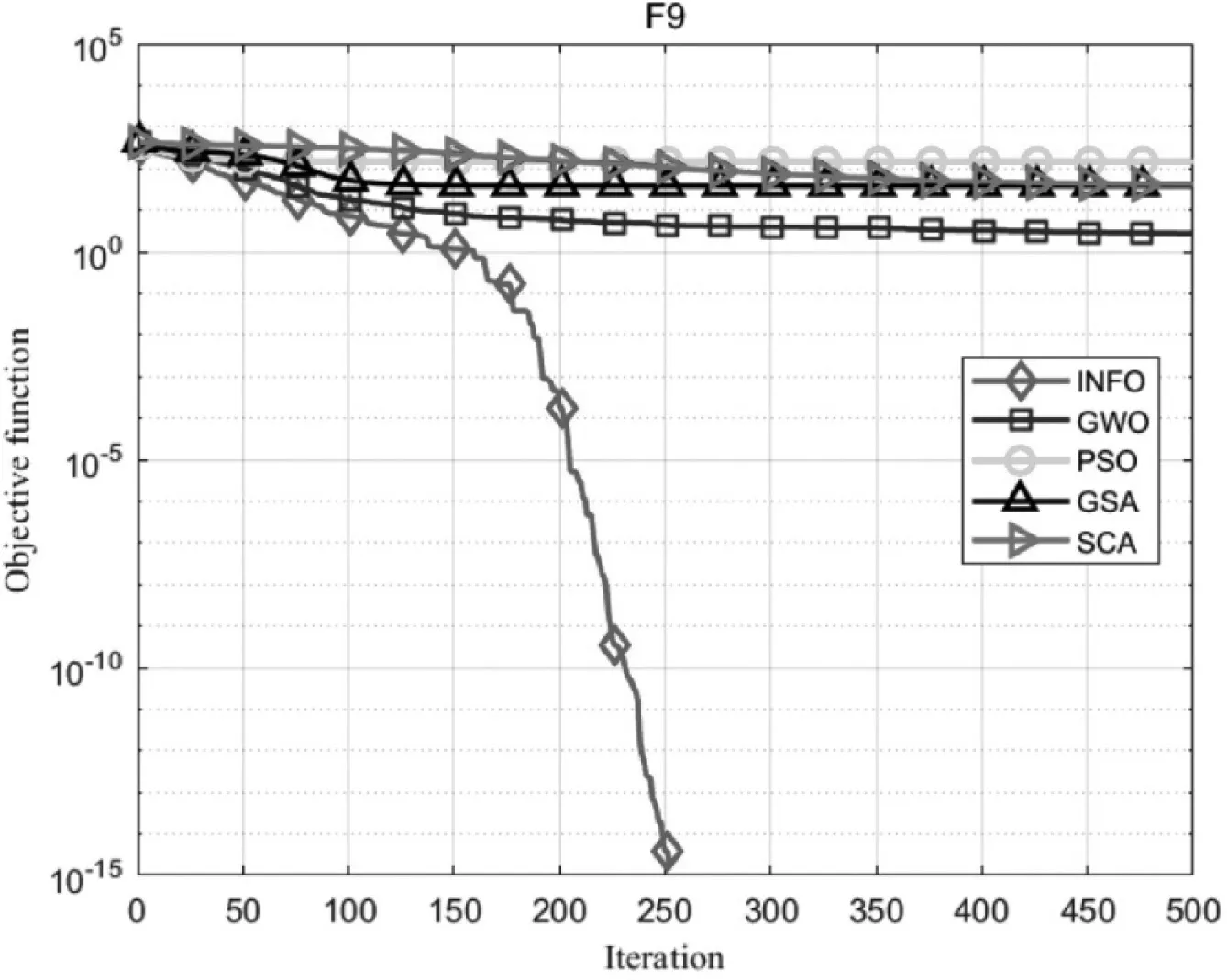
图2 函数F9(x)寻优曲线

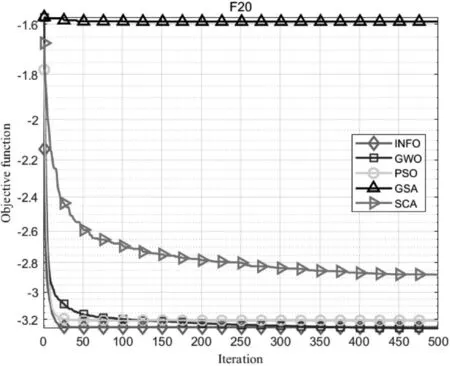
图3 函数F20(x)寻优曲线

2 INFO算法优化ELM的变压器故障诊断方法

2.1 ELM基本原理

ELM在训练时随机生成神经元的权重和偏置，并将数据输入到网络中，得到一个隐层的输出结果。接着，通过解线性方程组的方式求解输出层的权重，使得网络拟合训练数据的误差最小化。最后，利用得到的输出权重和隐层输出，进行测试数据的预测分类。具体地，ELM的计算过程如下：

式中：

L—隐藏单元的数量；

N—训练集样本数；

a—权重；

g—激活函数；

b—偏置向量；

x—输入向量。

由于激活函数的选取对于模型的分类结果有一定程度的影响，而高斯核函数（RBF）因为具有良好的泛化能力，所以选择的激活函数为：

2.2 INFO-ELM变压器故障诊断步骤

利用INFO优化算法对ELM模型中的超参数a和b进行寻优，从而提升ELM模型的故障诊断分类的准确率。基于INFO-ELM的故障诊断流程如图4所示。

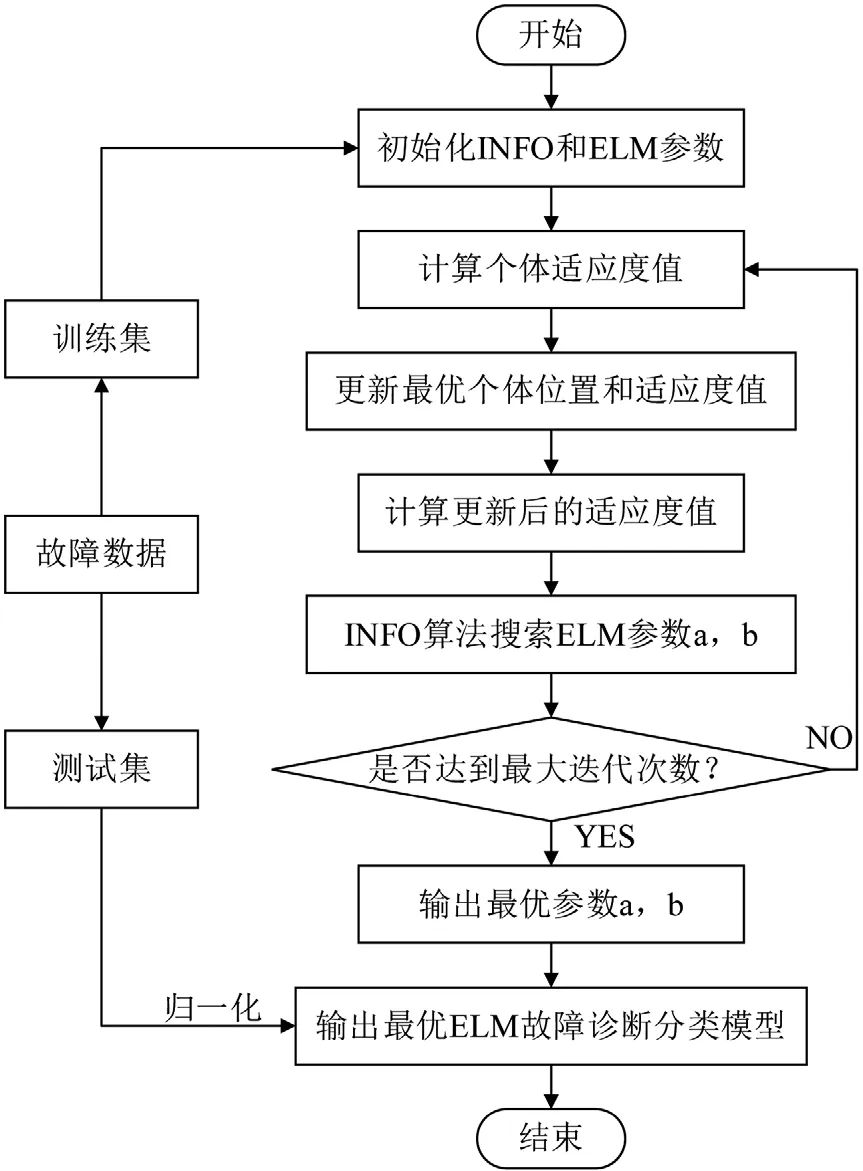
图4 INFO-ELM故障诊断流程

变压器故障诊断步骤具体如下：

1）数据预处理。对所选取的变压器故障数据集进行归一化处理。

2）初始化INFO和ELM的相关参数。设置初始种群数量、最大迭代次数以及各种边界约束条件。

3）更新规则，如公式（1）进行规则更新，计算个体适应度值，并进行排序，找出当前阶段最优向量的适应度值与位置。

4）向量合并，如公式（17）进行合并，生成新向量。

5）局部搜索，如公式（18）引入随机数，增强算法随机性。

6）计算最优个体适应度、位置。并进行条件判断，如迭代次数是否已经达到最大，精度是否满足使用需求等。如果条件满足，则输出最优参数a，b，输出变压器故障诊断模型；如果未满足相关约束条件，则继续计算。

3 结果分析

变压器在运行过程中，由于各种因素可能会引发降解、老化等问题，从而导致变压器故障，这些问题通常都会导致油中溶解气体的增加或减少，所以普遍使用油中溶解气体的含量对变压器故障进行分类。

我们选取H2、CH4、C2H2、C2H4和C2H6作为分析对象，数据集样本总数为375组，包含五种典型变压器故障类型，具体故障类型及样本分布如表2所示，所使用数据及部分数据及故障类型编码如表3所示。

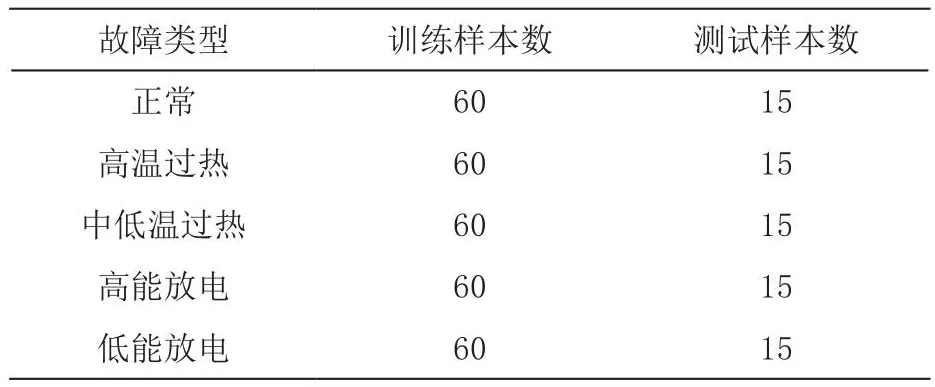
表2 数据集样本分布情况

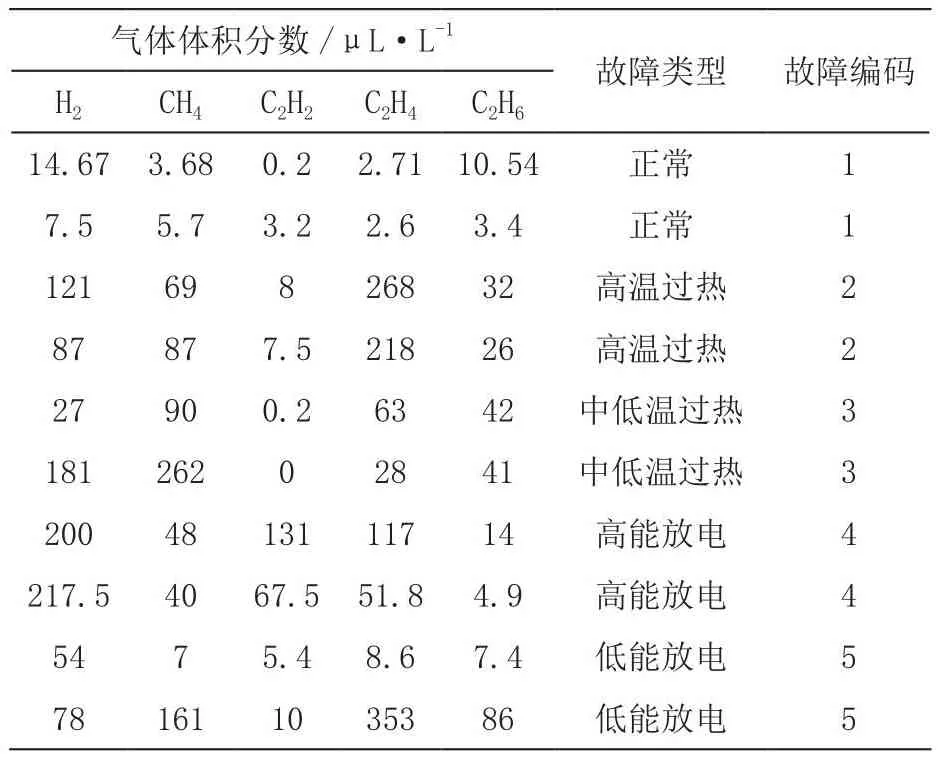
表3 部分数据及对应故障类型编码

利用本文提出的INFO-ELM故障诊断分类模型对变压器进行故障诊断，并与SVM、ELM、PSO-ELM、SSAELM、GWO-ELM故障诊断模型的结果进行对比，结果如图5～10所示，诊断准确率如表4所示。

图5 SVM故障诊断分类结果

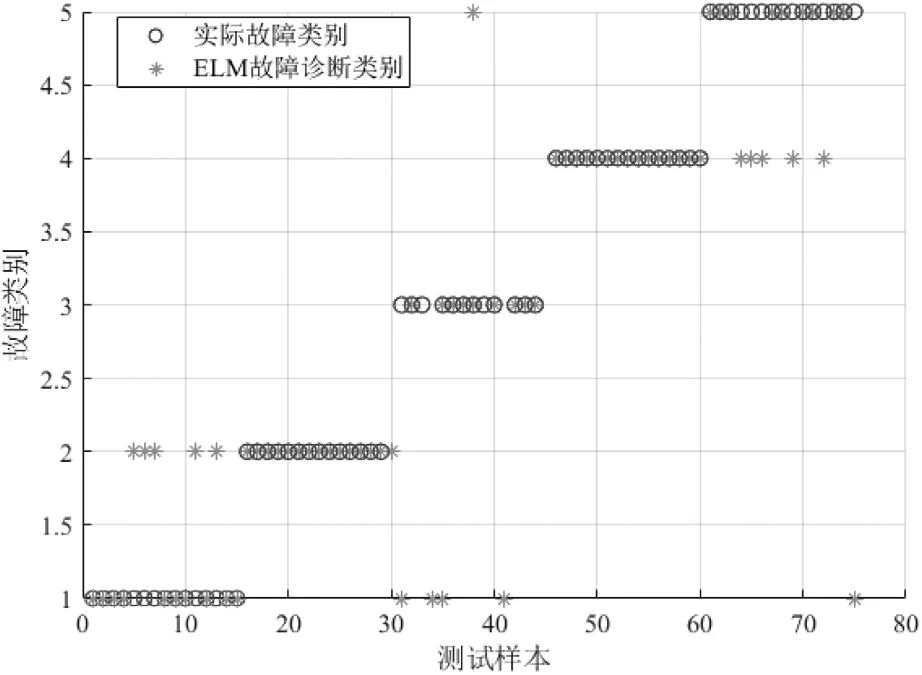
图6 ELM故障诊断分类结果

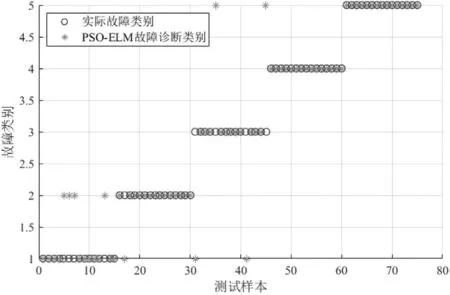
图7 PSO-ELM故障诊断分类结果

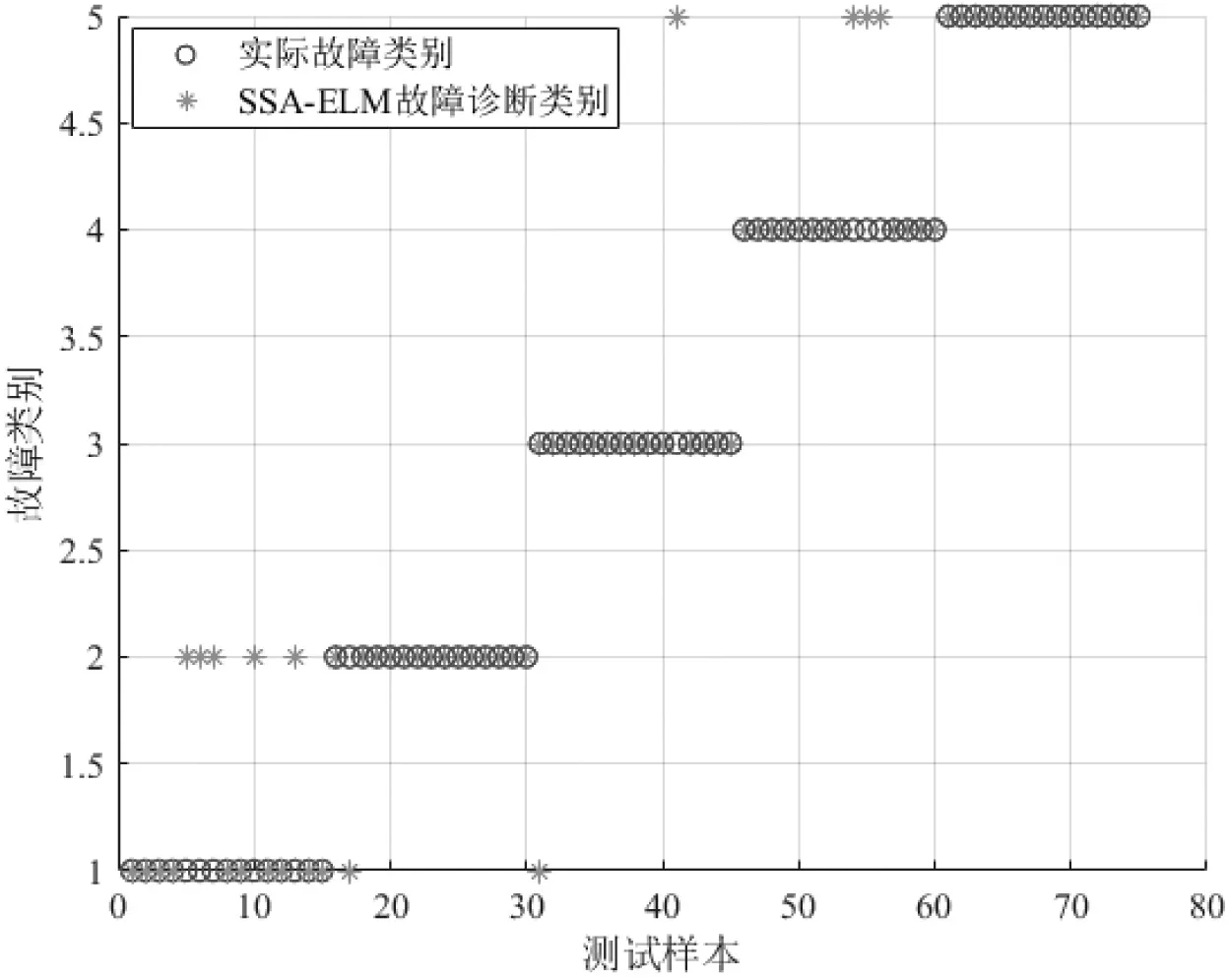
图8 SSA-ELM故障诊断分类结果

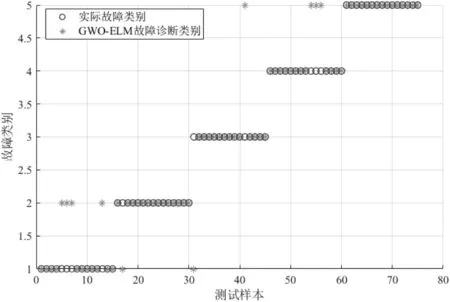
图9 GWO-ELM故障诊断分类结果

图10 INFO-ELM故障诊断分类结果

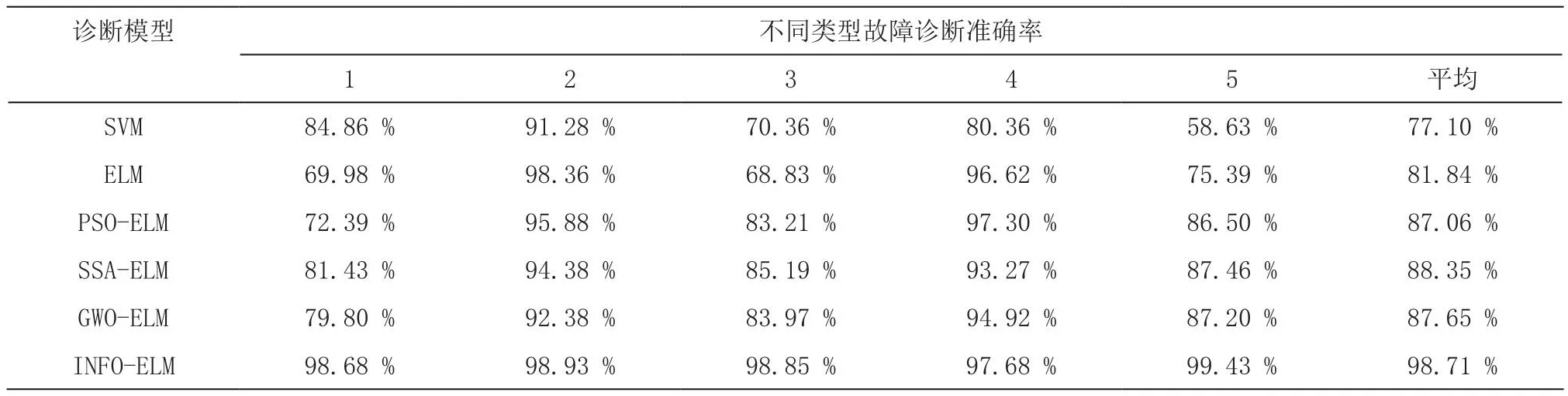
表4 不同模型的故障诊断准确率

综上，本文提出的INFO-ELM故障诊断分类模型针对变压器的故障诊断效果更好。

4 结论

本文提出了一种基于INFO优化ELM的变压器故障诊断分类模型，使用变压器油中溶解气体作为模型的输入，变压器故障类型对应的编码作为模型的输出，并与其他五种不同的故障诊断模型进行了对比测试，对所提出的INFO-ELM故障诊断模型的有效性进行验证，总结如下。

1）对INFO优化算法、PSO优化算法、GSA优化算法、SCA优化算法和GWO优化算法进行性能测试，结果表示INFO优化算法具有更好的寻优性能。

2）使用INFO优化算法对ELM中的初始输入权重a和偏置b进行优化，能够进一步提升故障诊断的精度。

3）通过与SVM、ELM、PSO-ELM、SSA-ELM、GWO-ELM模型的故障诊断结果可以看出，INFO-ELM故障诊断模型的平均诊断准确率为98.71 %，相较于其他五种模型分别提升了21.61 %、16.87 %、11.65 %、10.36 %和11.06 %，由此验证了本文提出的INFO-ELM模型在变压器故障诊断方面的可行性与良好的诊断分类精度。