基于路面激励的Adams车身柔性体影响研究
2023-12-01李太梅蔡剑王德远吴泽勋
李太梅,蔡剑,王德远,吴泽勋
(重庆睿蓝汽车研究院有限公司,重庆 401122)
引言
随着汽车工业的加速发展,企业车型更新换代的频率越来越快,因此对新车开发周期的时间要求也越来越严格,如何减少项目开发中耗时长的条目变成极为重要的事情。道路耐久试验条目耗时长,为减少耐久试验次数及时间,通过虚拟试验场VPG(Virtual Proving Ground)技术来进行前期模拟验证及优化,已经在业界广泛使用。影响VPG分析精度的主要因素是路面和轮胎,除此之外,车身及悬架部件是否考虑自身变形(也即是否柔性体)也是较重要因素。各车企大部分已经采用了柔性体,但柔性体应包含元素(如是否包含门盖等)以及柔性体理论上的影响暂未见到相关研究。
本文以考虑车身柔性的三自由度模型单轮模型为基础,进行了轮心载荷的公式推导,并将三种典型特征路面公式计算结果与VPG分析结果进行对比,结果说明了轮心载荷公式的指导性。之后基于公式对比车身不同柔性体方式结果,从理论上计算出了柔性体对分析结果的影响程度。
车身柔性体有三种方式,一是以完整TB(Trimmed Body)模型为基础进行柔性体计算,二是基于BIP(Body In Prime),仅保留白车身及仪表横梁模型,其他所有附件均以质量点形式连接,三是柔性体刚性化(刚体),前两种柔性体如图1所示。
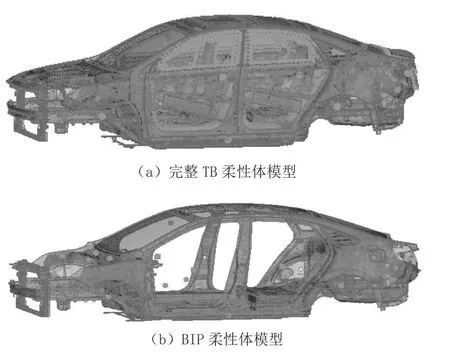
图1 柔性体模型示意图
1 理论公式
1.1 传递函数模型
为对整车模型进行简化,使用考虑人座椅等车身柔性的单轮简化模型为三自由度系统振动模型,如图2所示,mp为一个车轮上对应的座椅和人体质量,kp和cp分别为座椅弹性系数及阻尼系数,mb为一个车轮上对应的除人座椅外的其他车身质量,ks和cs分别为车身悬架弹性系数及阻尼系数,mu为簧下质量,kt为轮胎刚度。
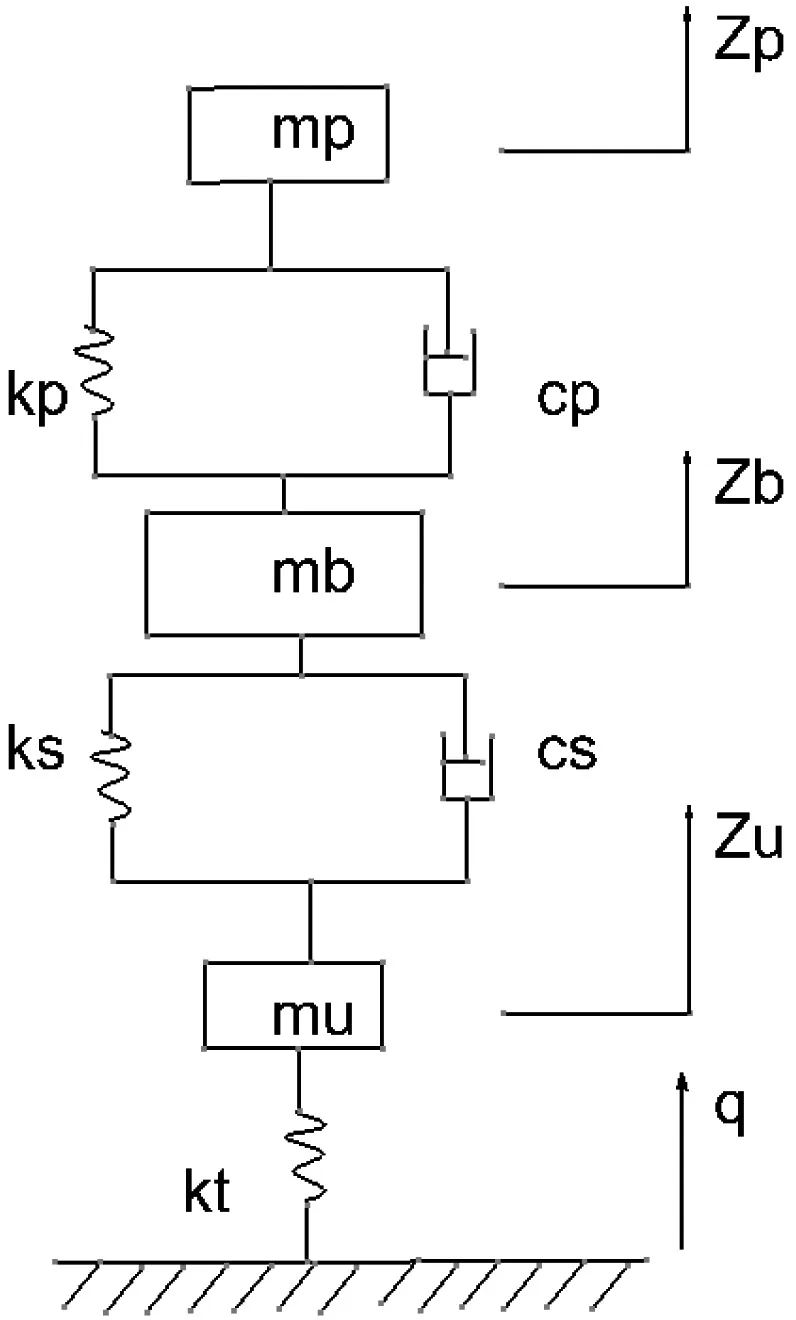
图2 考虑车身柔性的三自由度单轮模型
根据振动微分方程可以得到车轮动载对路面不平度的传递函数H(jw)Fd-q=kt*(D-N1)/D,式中的D及N1如下式所示。
式中:
s=jw,ξp—座椅人体阻尼比;
wp—座椅人体无阻尼固有频率;
ξb—车身阻尼比;
wb—车身无阻尼固有频率;
wt—无阻尼车轮固有频率。
1.2 路面分类
试验场路面根据频率分布分为两类,一类是随机路面,路面频率分布整个频段;另一类是非随机离散路面,频率在固定范围内。其中非随机离散路面又分为两类,一类是低频离散路面,路面激励频率较低;另一类是高频离散路面,路面激励频率较高。本文选择的随机路面为比利时路,低频离散路面为扭曲路,高频离散路面为振动路。
1.3 车轮动载计算公式
1.3.1 随机路面动载计算公式
针对随机路面,可以计算其响应均方值,均方值与传递函数及激励频率谱密度函数相关,公式如下所示。
式中:
1.3.2 非随机离散路面动载计算公式
针对非随机离散激励路面,激励可用多个正弦函数组合来描述,响应函数与激励函数曲线一致,仅幅值和相位区别。假设路面激励公式为q= q0*sin(wt),则响应公式Fd=|H(jw)Fd-q|*q0*sin(wt-ψ),ψ为传递函数相关联的相频滞后值。
2 车轮动载计算值与仿真值对比
2.1 比利时路对比结果
2.1.1 均方根值比较
根据项目输入参数轴荷、偏频、悬架刚度、轮胎刚度、座椅刚度、路面不平度、车速等参数,参考公式3可得到表1计算结果,得到轮胎动载Z向均方根值,轮心实际载荷Z向均方根值在轮胎动载基础上考虑静载得到。

表1 轮心载荷均方值计算表
VPG分析比利时路面轮心均方根值为5 345 N。
2.1.2 频域比较
虚线为公式计算功率谱密度曲线,与VPG分析轮心载荷PSD对比图如图3所示。

图3 公式计算轮心PSD与VPG分析PSD对比图
2.2 扭曲路对比结果
2.2.1 时域比较
使用MATLAB对扭曲路激励曲线进行函数识别转化,然后计算传递函数及激励函数可得到动载响应函数,计算结果与VPG分析结果对比如图4所示,其中虚线为计算曲线。
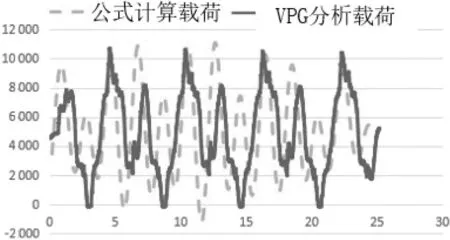
图4 扭曲路轮心计算时域曲线与VPG对比图
2.2.2 频域比较
公式计算功率谱密度曲线与VPG分析轮心载荷PSD曲线波形接近,共振频率分别为0.98 Hz和1.01 Hz。
2.2.3 伪损伤比较
以VPG分析轮心载荷为比较基础,公式计算载荷与VPG分析载荷相对损伤为1.43。
2.3 振动路对比结果
2.3.1 时域比较
使用MATLAB对振动路激励时域曲线进行函数识别转化,然后根据传递函数及激励函数可计算得到动载响应函数,计算结果与VPG分析结果曲线如图5所示,其中虚线为计算曲线。
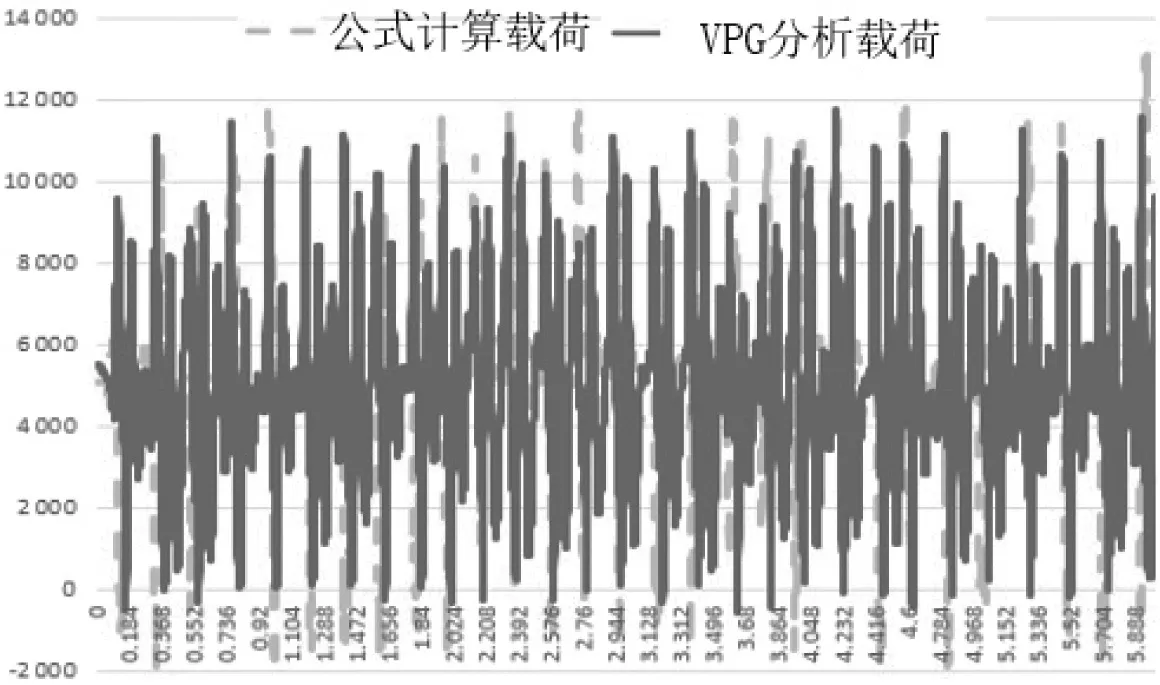
图5 振动路轮心计算时域曲线与VPG对比图
2.3.2 频域比较
虚线为公式计算功率谱密度曲线,与VPG分析轮心载荷PSD对比图如图6所示。
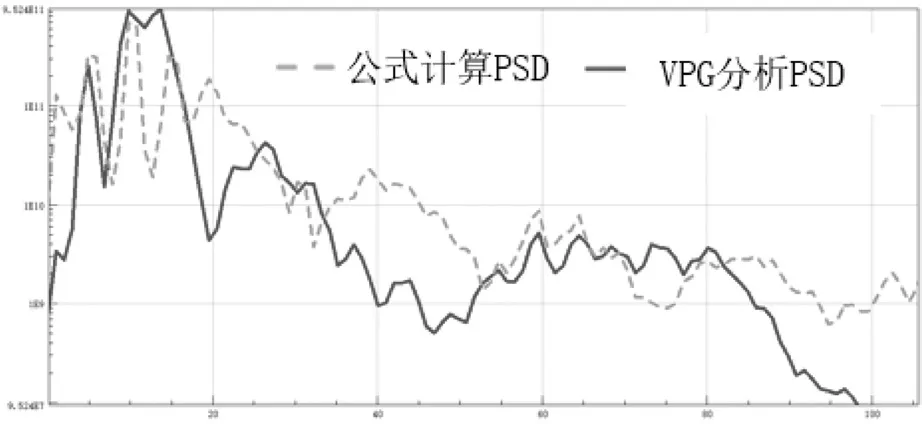
图6 振动路轮心计算频域曲线与VPG对比图
2.3.3伪损伤比较
以VPG分析轮心载荷为比较基础,公式计算载荷与VPG分析载荷相对损伤为1.13。
2.4 总结
由表2和图3~5对比图可以看到,随机路面公式计算轮心载荷与VPG分析值接近,非随机离散路面相对损伤在可接受范围,公式计算与VPG分析时域内曲线波形接近,频域内共振频率一致,说明简化模型及公式具有一定指导意义,可以基于简化模型公式对车身采用不同柔性化方式的结果进行计算对比。
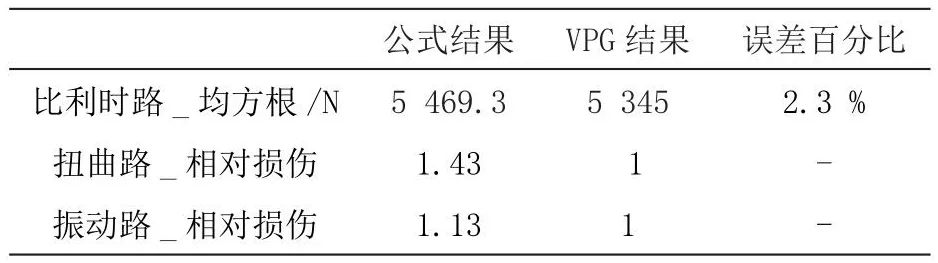
表2 轮心载荷对比表
3 不同柔性体结果对比
针对车身不同模拟形式,表现方式为对人座椅系统进行频率变化,TB柔性体人座椅频率使用项目输入质量及刚度计算,BIP柔性体则将此频率人为提高,刚体模拟方式则将此频率进一步极大提高,各方式对刚体的比较结果如表3所示。
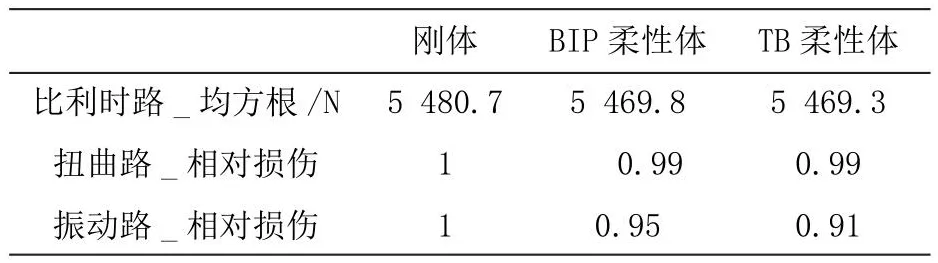
表3 轮心载荷计算对比表
以振动路为例,轮心载荷时域对比曲线如图7所示,曲线从上往下分别是刚体结果、BIP柔性体结果、TB柔性体结果。
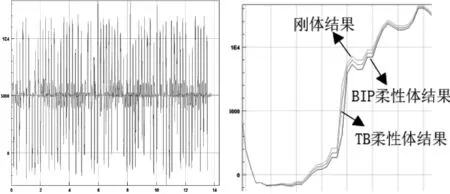
图7 不同模拟方式下振动路轮心计算时域曲线对比图
从表3和图7对比图可以看到,刚体车身在随机路面轮心均方值最大,在非随机离散路面轮心相对损伤越大,BIP车身柔性体模型次之,TB车身柔性模型均方值及相对损伤最小。因此,为更真实模拟车身变形对载荷影响程度,建议使用完整的TB柔性体模型,不做任何简化。
4 结束语
本文基于悬架三自由度简化模型搭建了轮心载荷理论计算流程,并将计算结果与VPG分析结果进行对比,说明了简化模型及公式的可用性及指导性。基于简化模型和公式,计算了车身不同模拟方式下对应的轮心载荷变化情况,从理论上看到车身模拟越刚性载荷越大,因此,为更真实模拟变形情况,建议使用完整的TB柔性体模型。
