McNemar检验的问题与应用*
2023-11-30耿瑞瑞李慧君丁伯春汤在祥
耿瑞瑞 李慧君 白 璐 丁伯春 汤在祥
苏州大学苏州医学院公共卫生学院流行病与卫生统计学系(215123)
【提 要】 McNemar检验是配对计数资料中检验两种处理是否有差异的常用方法,但该检验的结果只依据不一致的部分,并未充分利用样本所提供的全部信息,而且样本量过大,可能会出现结果与真实情况不符,即阳性率有统计学差异,而实际并无差异的情况。由于该检验应用范围广,且在多数统计教材中未明确指出该局限性,为了使初学者或者临床研究者更加全面了解McNemar检验,文章通过具体简便的案例,阐述McNemar检验在应用中存在的问题,以及目前的改良方法和应用该检验比较灵敏度和特异度差异的前提条件。旨在帮助使用者可以正确合理地选择该检验处理配对设计资料,避免产生错误的推论。
在医学研究中,经常会遇到四格表的配对设计资料,常见的形式有[1]:同一对子内两个个体接受不同的处理;同一批样品用两种不同的方法检测;以及同一个个体,接受处理的时间(前后)或位置(左右臂)不同等。针对上述资料,若比较两种结果的阳性频数分布是否相同(即两样本率或构成比的比较),采用的统计方法是配对卡方检验,也即McNemar检验。
关于McNemar检验,在目前通用的医学统计学书籍上,一般是针对两种检测方法的检查结果或者阳性率有无差别做假设检验。如文献[2-3]中,假设检验是两种检测方法的“阳性率或者阳性概率”是否有差异;而文献[4-5]中,其假设检验是“检查结果”是否有差异。从McNemar检验公式可看出,针对“检查结果”是否有差异做假设检验时,错误地将检验范围扩大了,因检查结果既包含阳性结果也包含阴性结果,而McNemar检验仅仅是在阳性结果基础上的检验,因此针对“检查结果”做假设检验是不合理的。但若不考虑总样本量,直接对“阳性率或者阳性概率”做假设检验,在应用中也可能得到错误的结论。在配对设计研究中,可能会出现经McNemar检验后阳性率相同,但实际是检查结果完全相反的情况[6],同时也可能遇到阳性率有统计学差异,实际并无差异的研究[7]。所以,对阳性率或检查结果下结论时,还需考虑应用条件及实际意义。本文主要通过案例清晰地解释该检验的缺陷,并列举出目前的改良方法和推荐应用场景。从而使临床研究者对于配对研究可以更准确地进行评价。
McNemar检验及其存在的问题
1.McNemar检验
McNemar检验是在1947年提出的用于四格表配对设计资料的检验[8]。在应用McNemar检验前,需先根据资料,整理成四格表,形式如表1。

表1 配对设计的四格表

当b+c≥40时,
(1)
当b+c<40时,校正公式为:
(2)
2.McNemar检验存在的问题
从表1及公式(1)、(2)可看出,该检验只反映在b和c提供的信息上,与a和d无关,与总样本数n也无关。即该检验仅仅只考虑了检测结果不一致的对子数,并未充分利用全部信息,因此有些情况就不能如实反映。在应用中,可能就会遇到以下问题:


表2 两种检测方法检测结果情况(n=100)
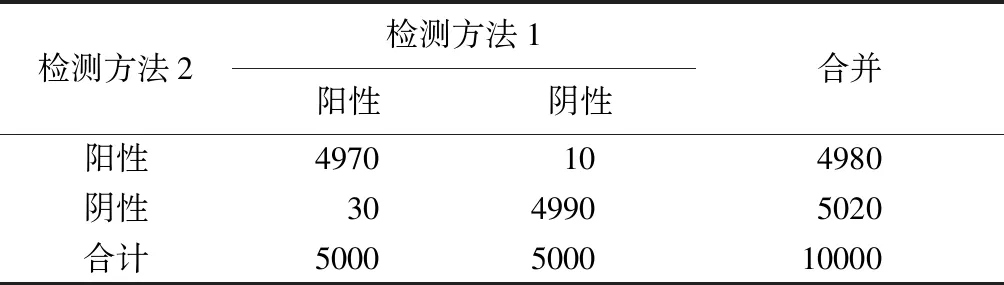
表3 两种检测方法检测结果情况(n=10000)


表4 两种检测方法检测结果情况(检测结果相似)

表5 两种检测方法检测结果情况(检测结果相反)
McNemar检验的改良与应用
1.McNemar检验的改良
上述问题也已经引起了国内外诸多学者的关注,并且提出了一些相应的解决方法。比如早在1995年,国内学者Lu[10]提出的McNemar检验的合理修正公式:
(1)陆修正公式

(3)
或者
(4)
该公式是在原公式的分母上增加了修正项,把总样本量以及一致部分(a和d)的数据信息纳入进去。通过计算可发现其结果比原检验的结果小,且随着样本量的增加,结果越来越小。陆运清[12]在文中也抽取几篇研究,将他们的数据用修正公式重新检验,所得χ2值与原文相比均有不同程度的减小,也即说明修正后的检验纠正了因仅考虑不一致部分而放大差异性的问题。
(2)W检验
王敏于2016年根据新方法证明McNemar检验,得到新的改进公式[13],即W检验,公式如下:
(5)

运用修正公式对本文表2、表3中不同样本量及b和c所占比重不同的案例进行检验,所得结果见表6。

表6 不同修正公式的检验结果
由以上结果可知,当b和c不变,样本量n增大时,运用陆公式得到的结果虽然会减少,但是b和c对结果依然有较大的影响。在b和c一定的情况下,W检验的卡方值随着a和d的增大而减小,对于表3案例,运用W检验,所得P=0.841>0.05,即两种检验方法之间没有差异,这个结果更具有合理性。所以,对于b和c比重较低,且有较大样本量的研究时,可选择采用W检验判断两种方法是否有差异。但对于样本量不大的研究,需谨慎选择修正公式。如研究评价两种方法对副溶血性弧菌的识别能力[14],根据三个公式可得卡方值结果见表7。
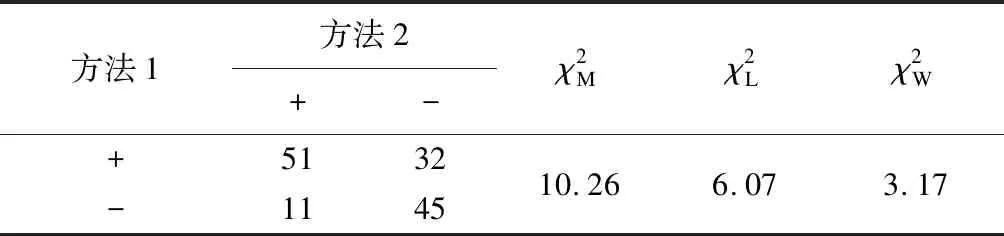
表7 文献中三种修正公式的检验结果

除上述改良方法之外,罗明奎[15]提出的改进方法,在四格表中a、b、c、d数据相差不大时,与McNemar检验的结论一致,但当b、c相对于a、d较大时,选用改进方法更符合实际情况。在2004年,Agresti[16]比较了McNemar检验和研究者们推导出的其他用于检验四格表统计方法的差异。wu[17]在2019年发表的文章中也对McNemar做了稳健性调整,提出的修正McNemar检验可以适用于样本量较小的研究。
2.采用McNemar检验进行灵敏度和特异度比较
(1)灵敏度和特异度比较
在实际应用中,McNemar检验除可比较阳性率差异外,通常也可用于比较两种检测方法的灵敏度和特异度的差异。如梁畅等[18]在探讨两种方法对乳腺“结构扭曲”样病变的诊断效能时,采用的即为McNemar 检验比较两种方法的灵敏度和特异度。但在做差异性比较之前,需先将样本根据金标准,分出患病组和非患病组,在患病组中检验灵敏度是否一致,在非患病组中检验特异度是否一致[6,19]。具体原理为:如表8数据显示的是应用金标准检测出的患病人群中和未患病人群中的结果。其中a为有病患者中两种检测方法均为阳性的患者数,d为有病患者中两种检测方法均为阴性的患者数,c为有病患者中检测方法1阳性,检测方法2阴性的患者数,d则为有病患者中检测方法1阴性,检测方法2阳性的患者数;未患病人群中单元格为a0、b0、c0、d0,边际总数为m0i、n0i(i=1,2),总数为n01。

表8 患病和未患病情况下两种检测方法的结果

(2)样本量估计
由表3可看出,当n很大且b和c相对较小时,即使检验有统计学意义,其实际意义往往也不大[23],因此应用该检验时需要有合适的样本量。在做配对的医学研究时,常需根据以下指标估算样本量[2,24]:确定检验水准α以及单双侧检验;期望的检验效能;由样本推断总体的信息以及预估的脱落率等。此外对于试验采用什么比较类型(如优效性试验、等效性试验或非劣效性试验),也是估计样本量的重要条件[25]。如比较两个方法的灵敏度是否相同时,可以使用公式(6)和(7)来确定所需的样本量[26],其公式如下:
(6)

(7)
其中η=(1-Se1)×Se2+(1-Se2)×Se1,δ=(1-Se1)×Se2-(1-Se2)×Se1,n1表示在n个总体中有n1个患病总体,p是样本中推测的疾病患病率,Se1、Se2是两个检验的灵敏度,Zα为正态分布累积概率等于α时的Z值,Zβ为正态分布累积概率等于β时的Z值。给出检验水准α,以及检验功效1-β,根据文献或者预实验确定Se1,Se2和p值,即可计算研究所需的样本量。比如,某传统的诊断试剂灵敏度为70%,现有一种新的有望提高灵敏度的方法,设计一项配对研究比较两种方法的灵敏度差异。已知该疾病在目标人群中的患病率为30%,期望新方法的灵敏度为90%,α为0.05,1-β为80%,带入公式计算出n约为160,假设预估的脱落率为10%,则得出此研究的样本量为178人。也可利用其他方法计算样本量,如黄[27]在评价SARS-CoV-2抗体检测试剂盒时,即根据灵敏度计算病例组所需的样本量、根据特异度计算对照组的样本量。
讨 论
McNemar检验不仅可用于配对设计资料的比较,也有研究显示,McNemar检验在行为生态学研究和其他领域也是可行的[28]。另外对于配对计数资料,McNemar检验并不是唯一的选择,还可用Pearson卡方检验做关联性分析[3]。也可采用Kappa一致性检验评价某种检测方法与金标准的一致性或评价两种方法结果是否一致[29],该检验与McNemar检验的主要区别是前者重点在于检验两种方法之间的一致性,而后者重在检验两者间的差异性。对于同一个样本数据,这两种检验可能得到相互矛盾的结论。比如一项基于体重识别有低血糖风险的婴儿与使用生长百分位曲线识别是否一致的研究显示[30],两种方法做一致性检验,显示中等一致,但做McNemar检验评估其差异性时,又显示差异有统计学意义。因此,在应用中需根据研究目的选择合适的评价方法。如对诊断试验资料进行分析时可以分为三个层面:(1)计算多个诊断性指标(如敏感性、特异度等)进行描述性统计;(2)采用Kappa检验考察试验方法检测结果与金标准的一致性;(3)采用McNemar检验考察试验方法测定的结果与金标准测定的结果不一致部分之间的差别是否具有统计学意义[31]。
综上,在应用该检验之前,需考虑样本的适用性,McNemar检验未考虑总样本量的大小,样本量过大,可能出现检验结果与实际结果不符的情况,所以该检验适用于样本量不太的资料。对于样本量大的研究,可以选择W检验的修正公式。也需考虑统计推论的合理性,公式中只考虑两种方法不一致的信息,未利用全部信息,因此,为防止出现阳性概率相同但检查结果相反的情况,可仅仅只对阳性率做统计推论。也可根据该检验是检验边际概率是否相等的特征,在患病人群、非患病人群中分别比较灵敏度和特异度的差异。
