透析平面运动刚体动能的计算
2023-11-29刘延彬
刘延彬
(安徽理工大学 力学与光电物理学院,安徽 淮南 232001)
概念是课程的基础,科学问题的分析及解决思想是课程的核心,为了提高平面运动刚体动能计算的教学效果,加深学生对平面运动刚体动能的理解,本文采用矢量分析的方法,给出刚体平面运动的动能计算公式.
1 平面运动刚体动能的统一形式
如图1 所示,做平面运动的刚体的质心为C,瞬时角速度为ω,取任意一点D为基点,其速度为.
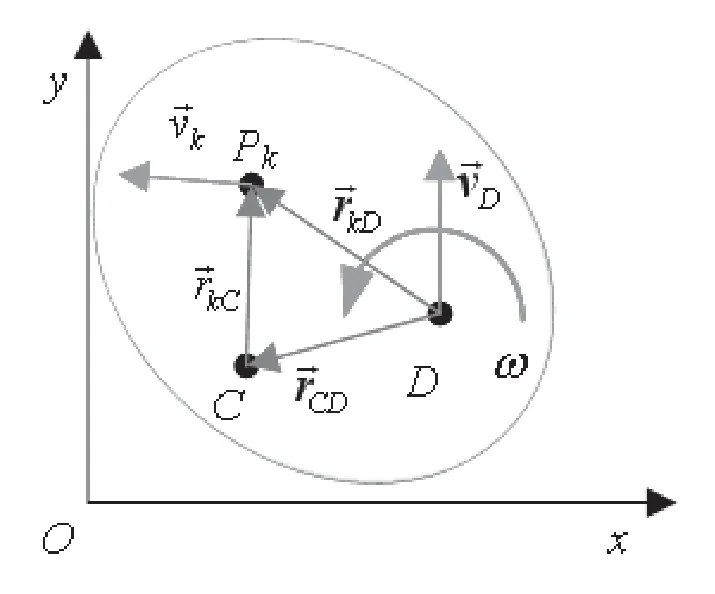
图1 刚体上任意点P 的速度
由于质点系的动能T为:
将(2) 式带入(1) 式可得:
将(4) 式带入(3) 式,可得:
由于C点是质心,在(5) 式中,,且,所以,
(6)式即为以任意点D为基点的刚体平面运动的动能计算公式. 设D点的速度方向与质心速度方向的夹角为,将(7)式写为标量形式为:
从(7) 式可以看出,以任意点D为基点的刚体平动动能计算公式与柯尼希公式不同,不但包含随基点的平动动能及围绕基点的转动动能,还包含了D点速度、质心速度及两种速度夹角余弦的乘积项,应用很不方便. 但是从(7) 式可以导出平面运动刚体各种形式的动能公式:
(2)当D点为速度瞬心时,将带入(7) 式,得到速度瞬心形式的动能公式:
(3)当D点为质心时,即D点与质心C点重合时,,得到柯尼希公式:
2 平面运动刚体动能计算教学
在运动学中[1-2],速度是一次函数,故可以简单的合成和分解,而动能是速度的二次函数,对于任意点为基点计算动能,不可以简单的叠加,只有质心具有特殊性.刚体平面运动可以分解为随基点的平动及围绕基点的转动,故其动能亦可以分解为两种动能,即随基点平动动能与围绕基点转动动能之和,这种理解是错误的.
对于刚体平面运动,以速度瞬心和质心以外的点为基点计算动能时,必须计算质心的速度.知道了质心的速度,完全可以采用柯尼希定理计算动能,且柯尼希定理相对简洁.对于平面运动刚体的动能,相对质心的转动惯量为确定值,只与刚体的几何形状及质量分布有关,而与时间无关;速度瞬心的时变性导致相对速度瞬心的转动惯量亦是时变的.在运动刚体上的不同瞬时瞬心点的轨迹称为瞬心动轨迹.[3]相对速度瞬心的转动惯量不是指某一个相对具体时刻的速度瞬心的转动惯量,而是指对瞬心动轨迹上所有速度瞬心点的转动惯量的集合,即相对速度瞬心的转动惯量是与瞬心动轨迹有关的函数,是时间的函数.由于瞬心动轨迹是关于时间连续的,所以相对于速度瞬心的转动惯量亦是时间的连续函数.
综上所述,学习过程中要注意几个问题:一是需要清楚质心及速度瞬心在动力学问题中的特殊性;二是刚体平面运动动能采用柯尼希公式计算;三是采用速度瞬心形式动能公式时,要知道相对速度瞬心转动惯量的时变性.
3 结论
分析了刚体平面运动的动能计算,给出与目前的理论力学教学体系兼容的推导过程,目的是提高平面运动刚体动能计算的教学效果,加深学生对平面运动刚体动能的理解.
