基于Debye模型的时间域航空电磁激电效应正演模拟
2023-11-29张鑫崇殷长春
张鑫崇,殷长春
吉林大学地球探测科学与技术学院,长春 130026
0 引言
时间域航空电磁法采用机载平台搭载电磁仪器,可以在沙漠、高山、沼泽、湖泊等地形条件复杂的地区进行勘探,是一种高效的地球物理手段,现已被广泛应用于矿产资源、地下水及环境工程等众多勘探领域[1]。与频率域电磁法相比,时间域航空电磁法对深部目标具有更好的分辨率和探测灵敏度[2]。
随着时间域航空电磁系统的进步和数据采集精度的不断提高,地球物理工作者们经常会遇见晚期道时间域航空电磁响应出现符号反转的现象,这种现象多发生在地下含硫化物以及一些含水地区。学者们认为该现象是由于激发极化效应引起的[3-5]。Weidelt[6]也进一步通过理论证明,对于共中心回线装置,时间域电磁响应数据晚期时间道中的符号反转现象出现的原因往往是激发极化效应。然而,传统的仅依赖电阻率的解释方法无法对该现象进行有效反演,给时间域航空电磁数据解释带来了一定的困扰。因此,时间域航空电磁法激电效应研究具有重要的意义。
近年,时间域航空电磁数据成像和一维反演解释技术已经趋于成熟。然而,实际情况下大地多为复杂的三维结构,一维成像和反演往往难以得到地下真实的电性分布结构[7-8]。因此,发展三维反演成为必然趋势。另一方面,正演是反演的基础,为对航空电磁数据进行有效解释,需要精确的正演算法。因此,本文将重点研究时间域航空电磁三维激电效应正演模拟。
针对激电效应的正演算法目前主要分为两大类。一种是基于频时转换方法[9-11],另一种是对麦克斯韦方程在空间和时间域直接进行离散[2, 12-13]。然而,傅里叶变换的精度受采样和变换方法的影响很大[14],因此直接求解时间域麦克斯韦方程受到了更多的关注。
在激发极化介质中,电导率与频率有关。Cole兄弟[15]在电化学研究中引入了复介电常数的表达式来描述液体的频散情况;随后Pelton等[16]在前人研究基础上,通过大量岩矿石测量结果,提出了国内外学者广泛采用的Cole-Cole模型,通过数学模型来描述均匀岩矿石由激电效应引起的复电阻率随频率的变化。目前,除了Cole-Cole模型[17-19],还有Debye模型[20-22]和Cole-Davidson模型[23]。其中,Debye模型是Cole-Cole模型的特例(频率相关系数c=1)[24],数学形式简单、最具代表性。本文选用Debye模型来描述岩矿石激电效应引起的复电阻率随频率的变化,进而对时间域航空电磁激电效应进行三维正演模拟。
在空间离散方面,本文采用基于非结构四面体网格的矢量有限元方法。该方法可以有效克服复杂几何形体和复杂起伏地形因建模造成的误差[25-26]。在时间离散方面,本文选用无条件稳定的隐式二阶后推欧拉离散格式。首先从麦克斯韦方程出发,采用二阶后推欧拉离散格式对传导电流和源电流密度时间导数进行时间离散;然后将Debye模型引入到欧姆定律中,推导出时间域欧姆定律表达式,进而利用二阶后推欧拉离散格式对欧姆定律中的时间导数进行离散,再利用非结构有限元方法对空间进行离散,建立方程进行求解;最后通过典型模型验证方法的准确性,并对异常响应特征进行分析。
1 方法原理
1.1 控制方程
时间域麦克斯韦方程可以写成:
(1)

(2)
式中:e(r,t)和h(r,t)分别为r处t时刻的电场强度和磁场强度;μ为自由空间磁导率,本文假设为自由空间值4π×10-7H/m;j(r,t)为传导电流密度;js(r,t)为源电流密度;d(r,t)为电位移矢量。式(2)中的右端第二项为位移电流项。航空电磁中由于位移电流远远小于传导电流,因此可以忽略不计[27]。将式(1)(2)联立并消去h,可得到如下方程:
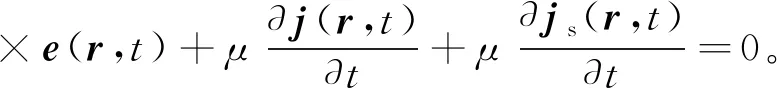
(3)
对于式(3)中的时间导数,我们采用无条件稳定的二阶后推欧拉离散格式进行近似,则传导电流密度和源电流密度的时间导数可分别离散为:
(4)
(5)
式中,时间步长Δtk-1=tk-tk-1。则式(3)可整理为
(6)
1.2 极化介质欧姆定律
传导电流密度可由欧姆定律描述,即
j(r,t)=σe(r,t)。
(7)
式中,σ为电导率,在非极化介质中是不变的。然而,当存在激发极化效应时,电导率是频散的,可用Debye模型[24]来描述:
(8)
式中:σ0为零频电导率;m为充电率;τ为时间常数;i为虚数单位;ω为角频率。此时,电流密度和电场强度不再满足式(7)简单的线性关系。下面推导极化介质中欧姆定律的形式。
首先我们给出极化介质中频率域欧姆定律,即
j(ω)=σ(ω)e(ω)。
(9)
则将式(8)代入到式(9)并整理可得
σ0e(ω)+iωτσ0e(ω)=j(ω)+iωτ(1-m)j(ω)。
(10)
应用傅里叶逆变换,式(10)可变换到时间域[2],即
(11)
式(11)即为极化介质中的欧姆定律,其左右两端均出现了时间导数。依然采用二阶后推欧拉离散格式对其进行离散,则式(11)可整理为
(12)
为方便后续推导,将式(12)相关系数用一些字符替代并整理为
(13)
其中:
将式(13)代入到式(6)中,即可得到电场的扩散方程为
(14)
1.3 有限元方法
本文使用矢量有限元法对式(14)进行空间离散。对于非结构四面体网格,第n个网格r处tk时刻的电场强度可表示为
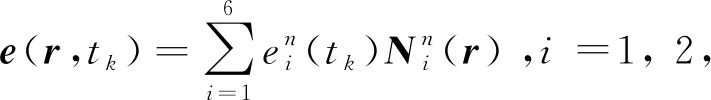
(15)
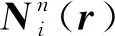
(16)
式中,j=1, 2, ⋅⋅⋅, 6。令加权残差Rn=0,并通过一系列代数运算,可以建立第n个网格的如下有限元方程:

(17)
式中,相关的矩阵可写为:
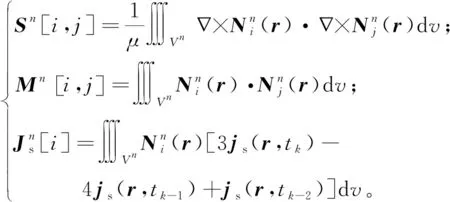
(18)
将全部网格的式(18)组装起来,可以得到tk时刻电场强度的稀疏对称方程组,即
[2Δtk-1S+3g1M]e(tk)=12g2Me(tk-1)-3g2Me(tk-2)-12g3Mj(tk-1)+3g3Mj(tk-2)+4Mj(tk-1)-Mj(tk-2)-2Δtk-1Js。
(19)
通过对式(19)施加Dirichlet边界条件n×e(tk)|boundary=0,可以得到最终的正演模拟方程为
Ae(tk)=b(tk)。
(20)
式中:A为系数矩阵;e(tk)为模型剖分网格单元各棱边上tk时刻的待求电场强度;b(tk)为tk时刻的右端源项。
我们使用直接求解器MUMPS求解得到各棱边的电场[28],而电场和磁场对时间的导数可以分别用矢量基函数及其导数通过插值计算得到。
2 数值算例
2.1 精度验证
为了验证本文算法的准确性,我们计算了均匀半空间条件下不同激发极化参数组合模型的电磁响应,并将结果与一维半解析解进行对比。本文采用中心回线装置(图1),系统参数设定如下:发射线圈(T)采用正八边形,半对角线长为15 m,发射线圈和接收线圈(R)高度均为30 m,发射电流为单位下阶跃波。

图1 航空电磁均匀半空间模型
空气电导率设为10-8S/m,分别计算不同均匀半空间电导率、充电率、时间常数的电磁响应,并与一维半解析解进行对比(图2—图4)。
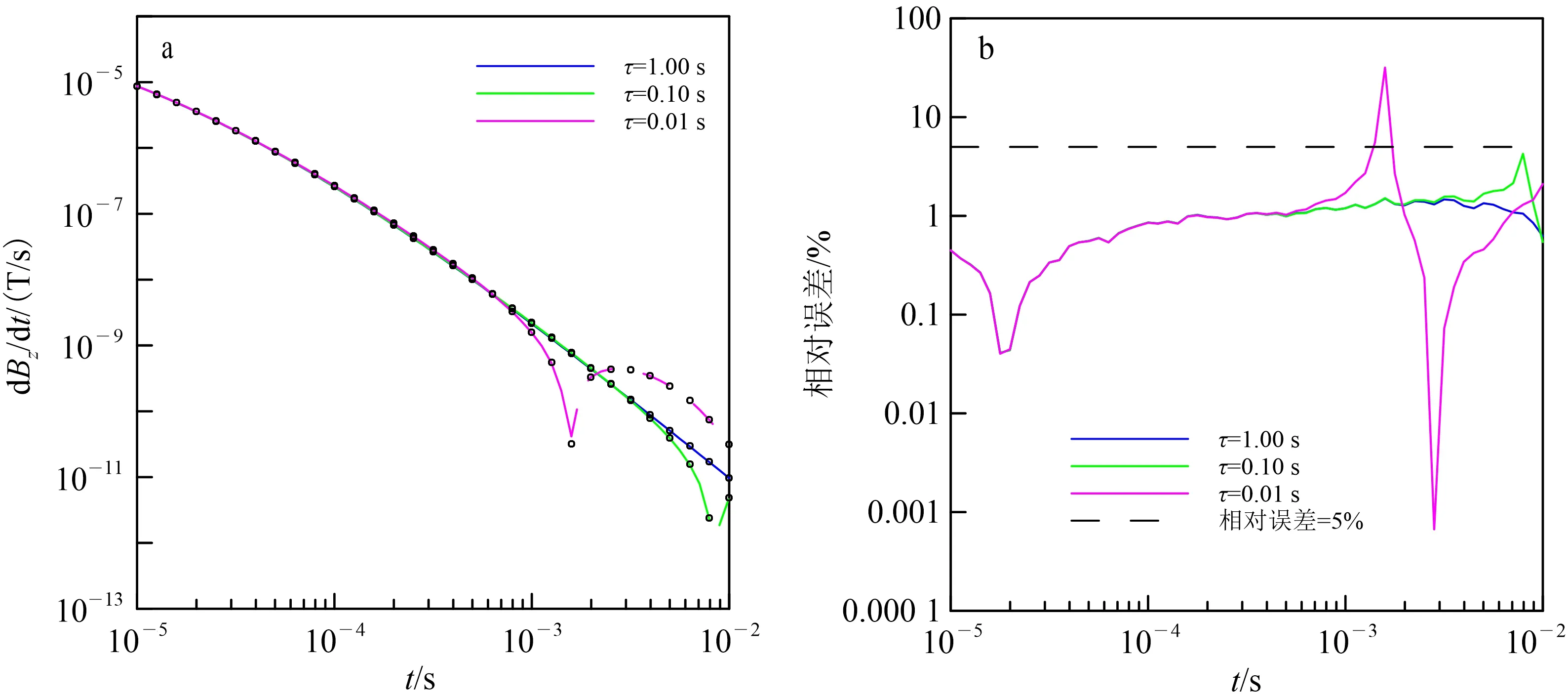
a. 电磁响应;b. 与一维半解析解的相对误差。σ0=0.010 S/m,m=0.8。图中实线代表正响应,虚线代表负响应,圆圈代表一维半解析解。
由图2—图4可知,本文三维正演计算的电磁响应与一维半解析解吻合很好,仅在符号反转区间内误差较大,其余区间的相对误差均在5%以内。通过分析发现,在符号反转区间内,电磁响应曲线数值急剧变化,此时无论是本文算法还是半解析解均无法获得精确结果。由此,我们验证了本文的三维正演算法的准确性。
2.2 典型地质体电磁响应
对典型地质体模型响应进行模拟,分别研究半空间、极化地质体、非极化地质体的响应特征,以达到识别地下地质体激电效应特征的目的,为航空电磁数据解释过程中的异常拾取和识别提供参考。为此,设计了如图5所示的水平板状体模型。水平板状体的尺寸为100 m×100 m×30 m,顶部埋深为30 m。飞行系统参数同上。
首先分别计算背景电导率为0.010 S/m的均匀非极化半空间、其中嵌入电导率为0.100 S/m的非极化板状体以及电导率为0.100 S/m的极化板状体的电磁响应(m=0.5,τ=0.01 s,图6a)。进而分别计算背景电导率为0.010 S/m的均匀极化半空间、其中嵌入电导率为0.100 S/m的非极化板状体以及电导率为0.100 S/m的极化板状体的电磁响应(m=0.5,τ=0.01 s,图6b)。
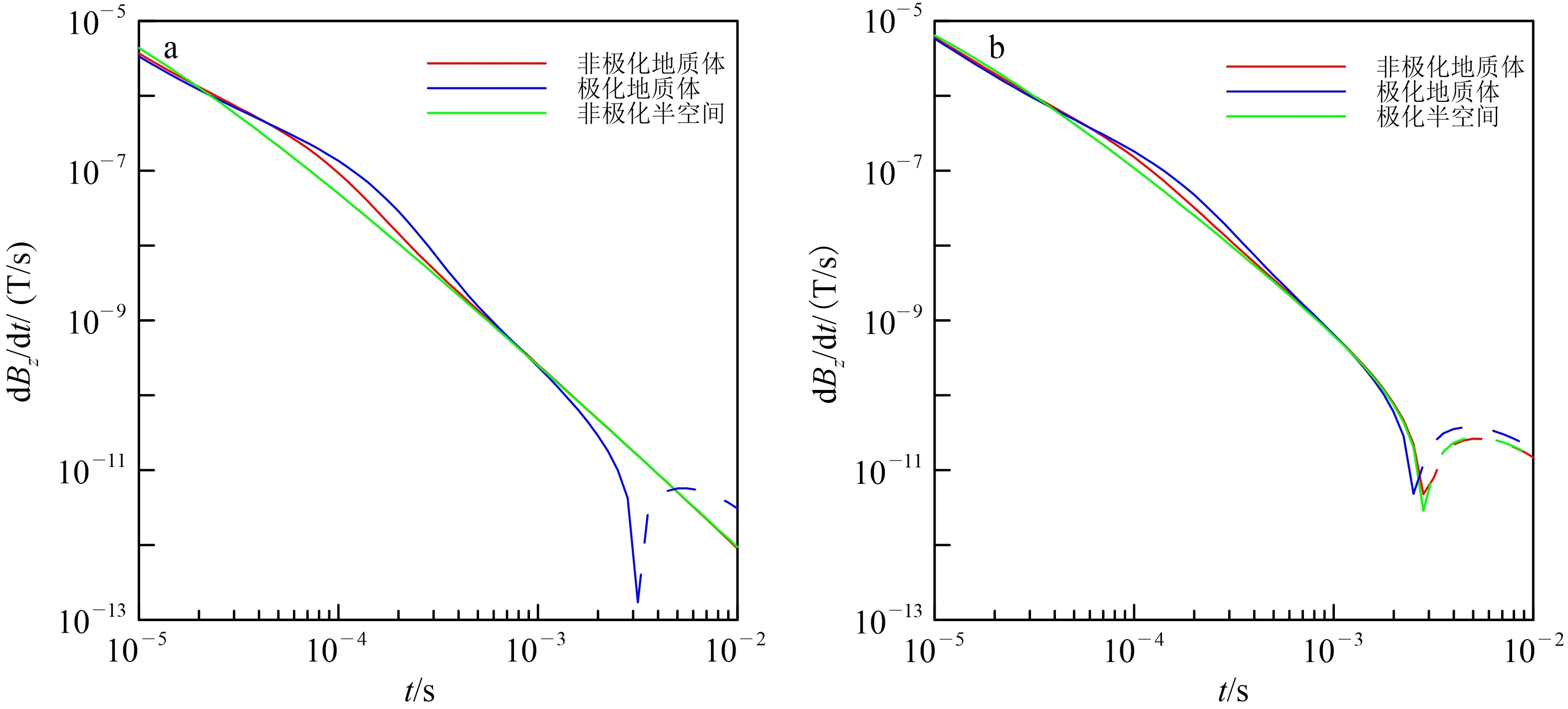
a. 非极化半空间;b. 极化半空间。m=0.5,τ=0.01 s。图中实线代表正响应,虚线代表负响应。
由图6a可以看出,在t=0.1 ms附近,极化地质体响应曲线衰减速度比非极化地质体慢,两者衰减速度均较非极化半空间慢,且晚期极化地质体曲线出现负响应。研究表明,在含有激电效应的地下介质中,时间域电磁响应可看成感应响应和极化响应之和[12]。分析可知,在t=0.1 ms附近,低阻地质体的存在导致电磁响应衰减变慢,由于极化地质体产生激发极化效应,且极化响应与感应响应同向,因此电磁响应衰减速度比非极化地质体更慢。由于极化地质体的存在,晚期会出现负响应。
由图6b可以看出,在t=0.1 ms附近,极化地质体响应曲线衰减速度比非极化地质体慢,两者衰减速度均较极化半空间慢,在晚期均出现负响应,且极化地质体负响应出现时间更早、幅值更大。由于极化围岩的存在,在晚期3条响应曲线均出现符号反转,而极化地质体的存在会使负值响应出现的时间更早、负值响应幅值更大。
根据曲线的这些特征差异,我们可以很好地识别地质体是否为极化体,为航空电磁数据处理中的异常拾取和识别提供参考。
2.3 极化参数对电磁响应的影响特征
为检验地质体电性参数对电磁响应的影响特征,本文建立一个三维地质体模型,讨论其极化参数对电磁响应的影响。电导率和充电率是影响电磁响应的主要参数,本文围绕这2个参数设计三维地质体模型。地质体尺寸为1 000 m×1 000 m×500 m,顶部埋深为100 m(图7)。
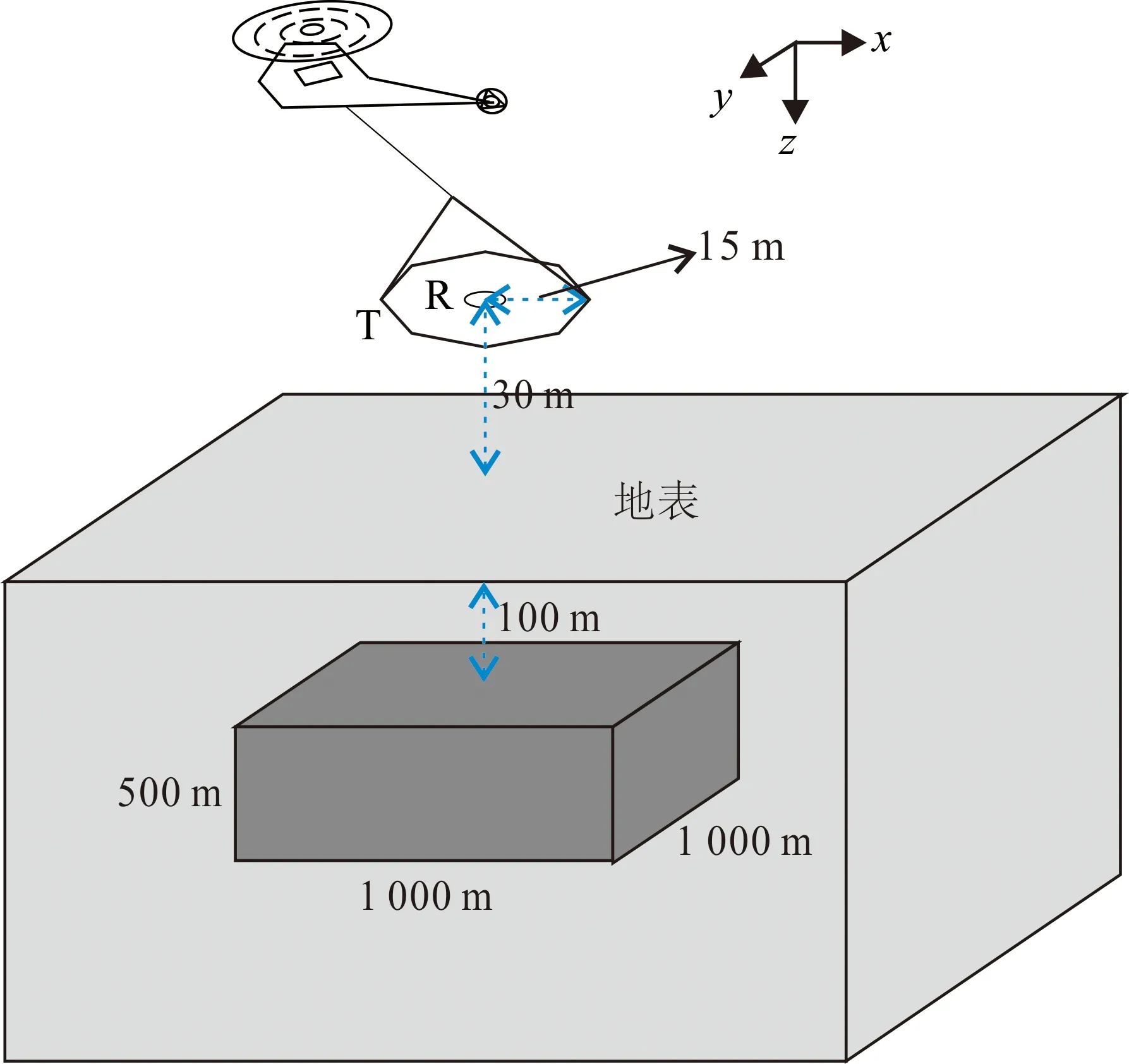
图7 三维极化地质体模型
首先研究极化体电导率对电磁响应的影响特征。假设极化体电导率分别为1.000、0.200、0.100和0.020 S/m,m=0.5,τ=0.01 s,空气电导率为10-8S/m,无极化围岩介质电导率为0.010 S/m。图8展示了不同电导率极化体时间域航空电磁响应。
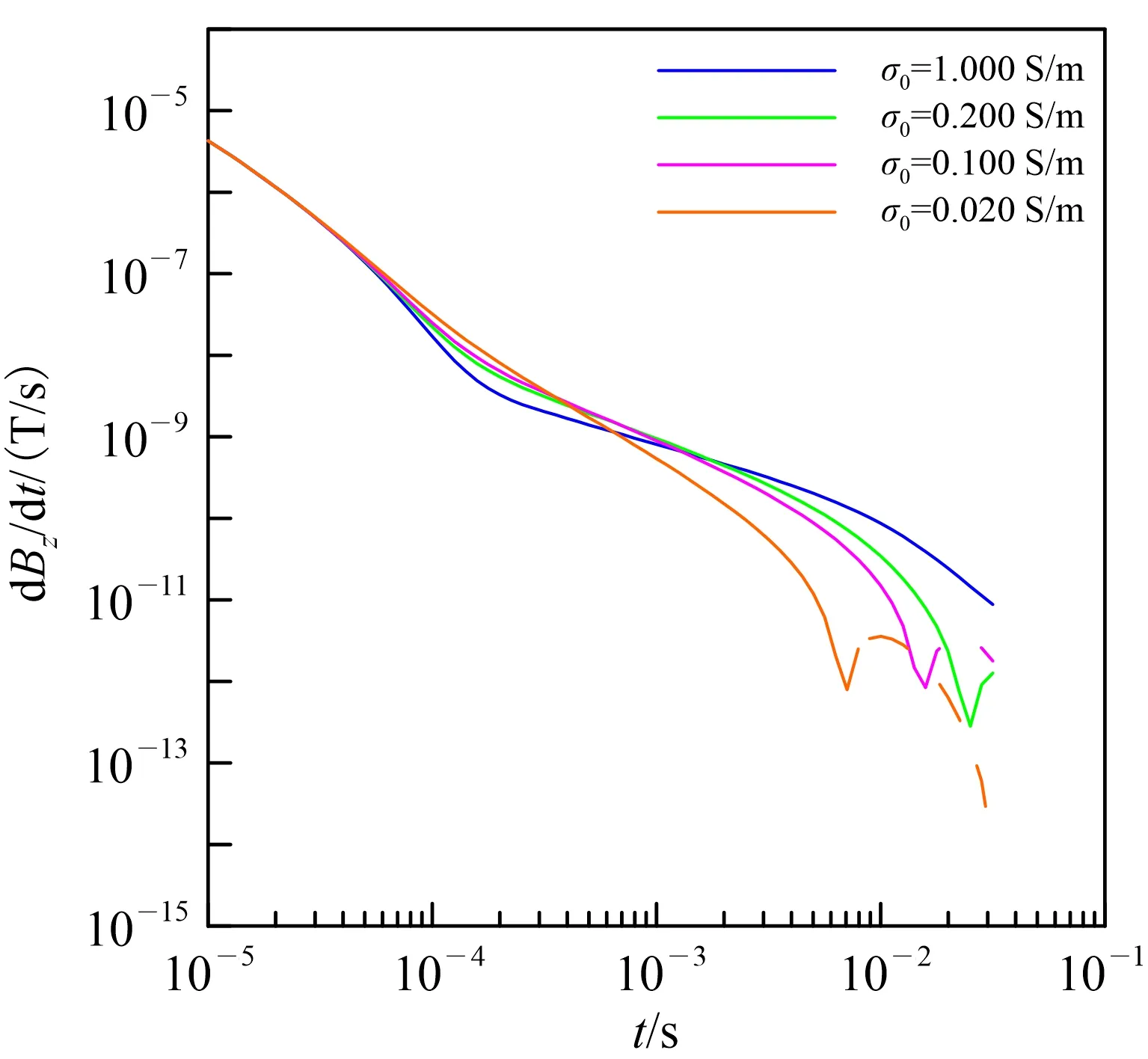
m=0.5,τ=0.01 s。图中实线代表正响应,虚线代表负响应。
由图8中给出的对比结果可以看出,地质体电导率越小,晚期负响应出现越早。这是因为地质体电导率越小,电磁波衰减越快,而由激发极化效应产生的负响应出现越早。
进而,我们研究极化体充电率对电磁响应的影响特征。假设极化体充电率分别为0.0、0.2、0.5、0.8,σ0=0.100 S/m,τ=0.01 s,空气电导率为10-8S/m,无极化围岩介质电导率为0.010 S/m。不同充电率极化体的电磁响应曲线如图9所示。
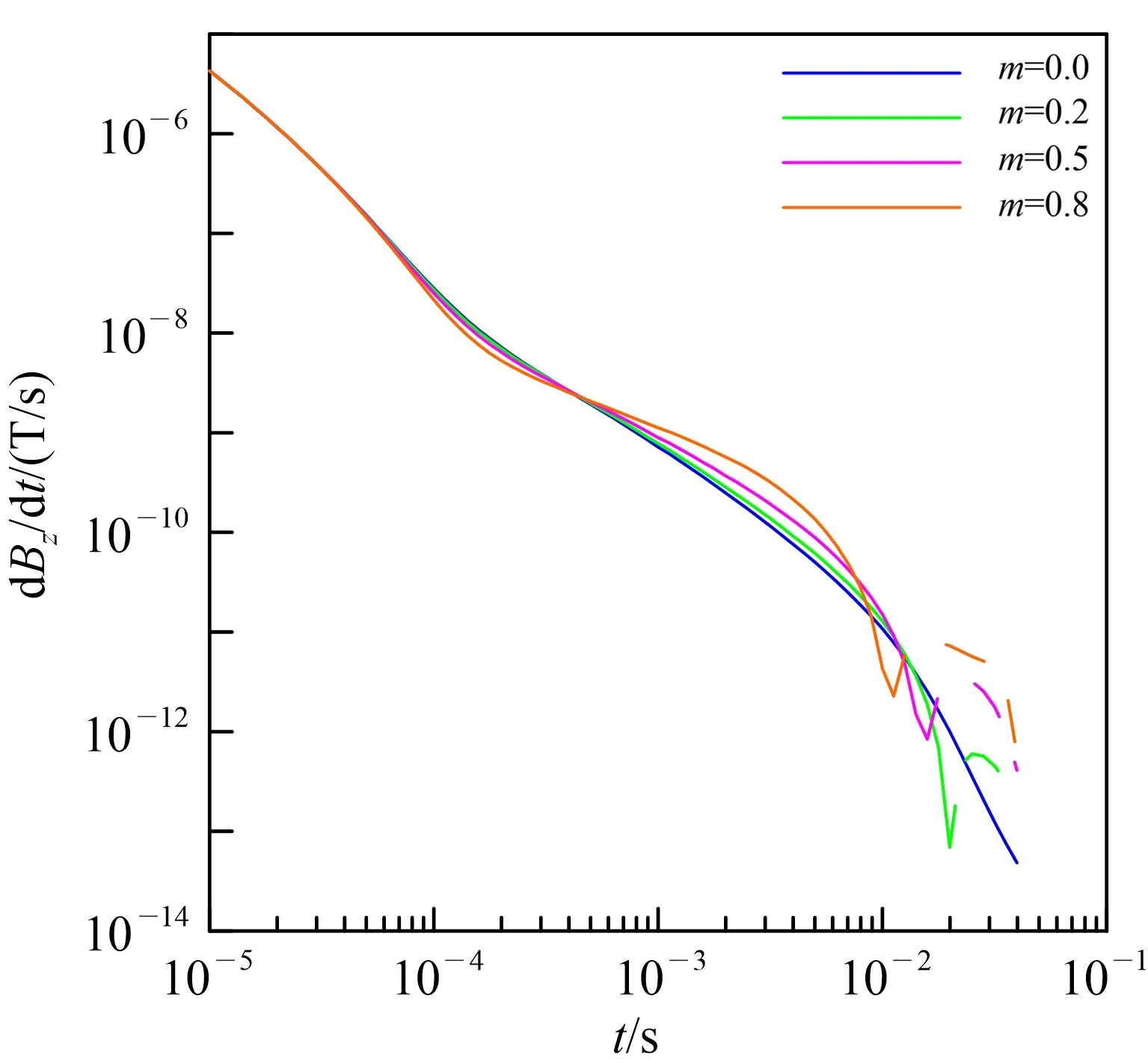
σ0=0.100 S/m,τ=0.01 s。图中实线代表正响应,虚线代表负响应。
由图9可以看出,除了非极化介质(m=0.0),其余3种模型均出现了电磁响应符号反转现象。地质体充电率越大,负值响应出现越早,且幅值越大。这是因为极化地质体充电率越大,激电效应越强,负值响应出现的时间也就越早。
3 结论
1)本文成功提出一种基于非结构有限元的时间域航空电磁激电效应三维正演方法。该方法针对极化介质将Debye模型引入到欧姆定律中,并应用二阶后推欧拉离散格式对时间导数进行离散,实现电磁场求解。
2)利用不同激发极化参数的半空间模型,验证了本文算法具有较高的计算精度。
3)计算了半空间和三维地质体具有不同的极化条件时的电磁响应,发现可以根据航空电磁响应曲线的衰减特征,有效地识别围岩及异常体的极化特征。
4)激电参数对时间域航空电磁系统的影响特征研究表明,地质体电阻率越高或者充电率越强,极化效应影响越严重。
期待本研究可为航空电磁的数据处理过程中的异常拾取和识别提供参考。
